2. 中国地震局地震工程与工程振动重点实验室, 哈尔滨市南岗区学府路29号 150080;
3. 福建省地震局, 福州 350003
2. Key Laboratory of Earthquake Engineering and Engineering Vibration, CEA, Harbin 150080, China;
3. Earthquake Administration of Fujian Province, Fuzhou 350003, China
气枪震源具有性能稳定、自动化程度高、成本低、易操控、可重复、高精度、无污染等诸多优点,已在海洋石油勘探中获得巨大成功,有关研究结果也成为20世纪末海洋地震勘探的重大成果之一。在海陆过渡带、内陆湖泊、海上OBS以及深海拖缆等水域地震勘探中,基本都是使用气枪作为震源(何汉漪,2001)。大容量气枪震源子波具有丰富的低频成分,通过重复激发和信号叠加提高信噪比,可将气枪震源应用于深部探测。地震学家利用海上气枪震源与陆地地震台站进行了联合实验,在深部探测研究中取得了很好的结果。英国BIRPS计划,法国ECORS计划,美国LARSE计划,新西兰SIGHT计划,德国、英国、丹麦、瑞典等国联合开展的Mona Lisa计划,日本东海海槽东部海陆联合地震探测就是利用气枪进行海陆联合勘探的成功实例(Woods,1995;Okaya et al,2002;罗桂纯等,2006)。国内也进行了南海东北部海陆联合深地震勘探、河北上关湖水库气枪激发实验、福建陆域及台湾海峡西部地区陆海联合探测实验等一系列利用大容量气枪震源进行深部探测的科学实验(丘学林等,2003;林建民,2008;唐杰,2008)。
利用气枪震源的高度重复性并结合高精度的观测系统,能够连续检测地下介质波速变化,从而为主动监测地下介质速度和应力变化及进行基于介质物理属性的地震预测提供新的思路。美国、土耳其等国科学家对此进行了相关研究(Brenguier et al,2008)。国内有关专家相继在河北遵化上关湖水库、云南宾川大银甸水库、新疆呼图壁人工水体等开展了水库气枪实验来探测地下介质的波速变化(王伟涛,2009;王宝善等,2011、2013;杨微,2013;杨微等,2013)。
为研究大容量气枪震源特性,2014年11月福建省地震局在福建省三明市尤溪县坂面乡街面水库(25.926°N,118.057°E)开展了大容量气枪激发实验,结合不同工况实验,研究了沉放深度、工作压力、气枪数量、枪阵尺寸、水体深度等因素对气枪震源子波特性的影响。本文介绍了街面水库气枪实验概况,并根据近场水听器波形记录,研究了气枪子波时频特性及其受沉放深度和工作压力的影响,还结合Johnson(1994)气泡模型解释了气泡振荡过程。
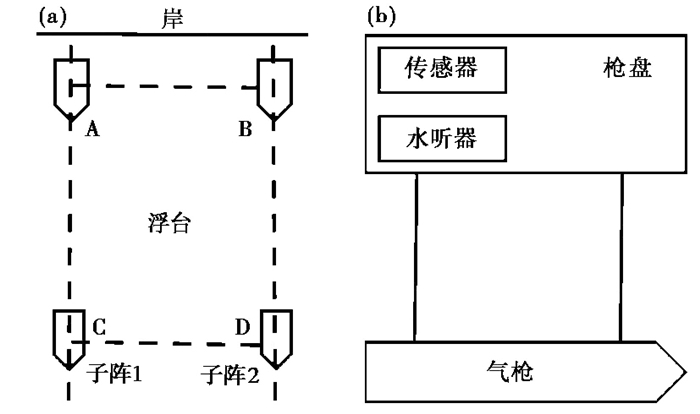
1 街面水库气枪实验概况2014年11月,福建省地震局在总库容为18.24亿m3的街面水库(25.926°N,118.057°E)开展大容量气枪激发实验。为获取满足深部探测需求的较高能量的低频信号,我们选择4支1500LL型Bolt枪组成气枪阵列。气枪单枪容量2000 in3,枪阵总容量8000 in3,工作压力2000psi。气枪阵列如图 1(a)所示,其中,气枪A、B两杆枪组成子阵1,C、D两杆枪组成子阵2,子阵1、2共同组成气枪阵列。枪盘如图 1(b)所示,在每杆气枪正上方2m处的枪盘上固定有近场水听器和枪压传感器,用于记录各枪近场子波和枪压信号。近场水听器采样率为1000Hz,每炮激发的记录时长为0.5s;枪压传感器采样率为10000Hz,每炮激发的记录时长为0.05s。
|
图 1 气枪阵列和枪盘示意图 (a)气枪阵列;(b)枪盘 |
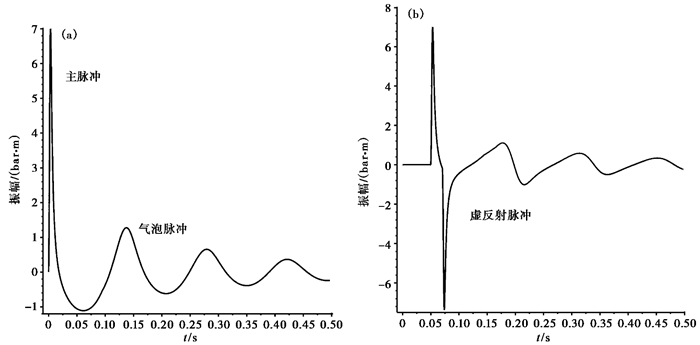
高压气体释放到水中,被周围的水围成一个近似球形的气泡,气泡在水中不断振荡直至衰减破裂,形成一系列子波脉冲。气枪子波由主脉冲和气泡脉冲2部分组成。对于远场子波,由于水面反射系数理论上为-1,因此,紧随正脉冲之后会形成1个负的虚反射脉冲。子波参数包括主脉冲振幅、气泡脉冲振幅、初泡比、气泡周期等。图 2为气枪子波示意图。
|
图 2 气枪子波示意图 (a)近场子波;(b)远场子波 |
(1) 主脉冲:主脉冲是指气枪内的高压气体释放到水中产生的第1个正压力脉冲。主脉冲能量大,频带宽,频率高,通常应用于浅层石油勘探,其振幅单位为巴·米(bar·m)。巴·米的含义是:以距震源中心1m处的声压值为度量单位来衡量气枪压力脉冲能量的大小。主脉冲振幅大小与气枪容量及工作压力等密切相关,是描述气枪阵列能量大小的参数,其值越大,表明气枪输出的能量越强。通常气枪容量越大,工作压力越大,产生的能量越强,主脉冲振幅越大。主脉冲振幅A存在如下经验公式(何汉漪,2001)
| $ A={{C}_{1}}{{V}^{\frac{1}{3}}}{{P}^{\frac{3}{4}}} $ | (1) |
其中,C1为常数;V为气枪容量;P为工作压力。
(2) 气泡脉冲:气泡脉冲由高压气体释放到水中形成的气泡振荡所引起。气泡振荡能量主要集中在低频段。由于气泡振荡会影响信号的分辨率,故在浅部探测中需削弱气泡效应。而深部探测要求地震波穿透深,传播远,需要足够的低频能量,因此需加强气泡效应。气泡效应的大小与气枪容量、工作压力、沉放深度、组合方式等有关。
(3) 初泡比:初泡比是指主脉冲振幅与第1个气泡脉冲振幅之比。初泡比越大,气枪子波频带越宽,频谱越光滑。在浅部探测中,通常初泡比不能小于10。初泡比随沉放深度的增加而减小,随气枪容量立方根的增大而增大。初泡比Pb经验公式如下(何汉漪,2001)
| $ {{P}_{\text{b}}}=\frac{{{C}_{2}}}{{{\left[ 34.73D{{\left(\frac{PV}{D+10} \right)}^{-1/3}}-1 \right]}^{1/2}}+0.2} $ | (2) |
其中,C2为常数;D为沉放深度。
(4) 气泡周期:气泡周期是指主脉冲与第1个气泡脉冲的时间间隔。气泡周期与低频段主频相对应,与气枪容量、工作压力、沉放深度等密切相关。气泡周期T存在如下经验公式(何汉漪,2001)
| $ T={{C}_{3}}\frac{{{P}^{\frac{1}{3}}}{{V}^{\frac{1}{3}}}}{{{(D+10)}^{\frac{5}{6}}}} $ | (3) |
其中,C3为常数。
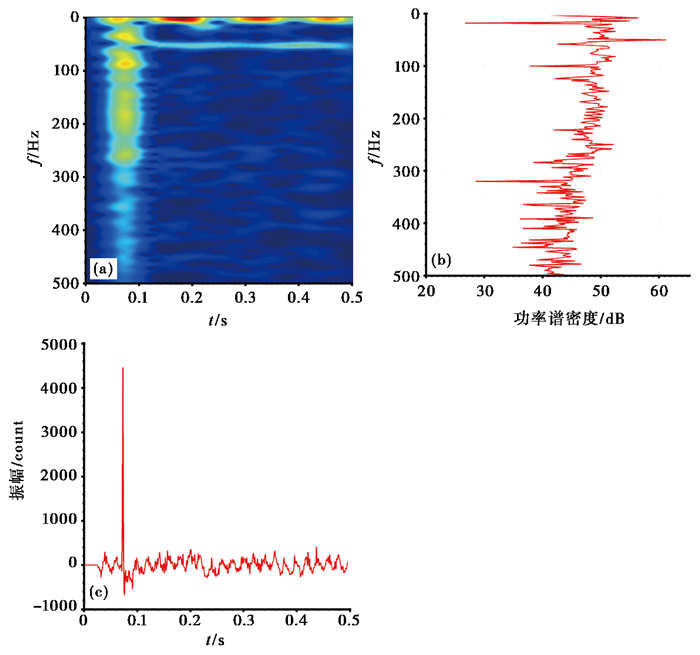
2.2 近场水听器记录的时频特性利用短时傅里叶变换(STFT)对近场水听器记录作时频分析,图 3为A枪在工作压力2000psi、沉放深度15m、水深45m的工况条件下单枪激发时近场水听器实测波形的时频分析,频带范围为0~500Hz。图 3(a)为时频谱,由图 3(a)可见,在时域0~0.1s、频域0~300Hz段为主脉冲,主脉冲持时短,频带宽,能量在0~300Hz段近似均匀分布;在时域0.15~0.50s、频域0~10Hz段,对应有3个能量分布明显的气泡脉冲;在频域50Hz处有明显的能量分布;同时,由图 3(c)的时域波形能清楚看到周期为0.02s的噪声干扰,考虑到中国交流电频率为50Hz,因此推测50Hz处的能量分布可能是电流噪声。从图 3(b)的频谱可以看到,由于噪声干扰,水听器记录的频谱并不光滑,有很多尖刺,50Hz处有明显的噪声干扰。图 3(c)的时域波形中主脉冲非常明显,气泡脉冲由于振幅相对较小且在电流噪声的干扰下,波形并不明显。根据图 3的时频分析,我们对近场水听器记录进行时频滤波,保留0.05~0.10s、0~300Hz的主脉冲,以及0.1~0.5s、0~15Hz的气泡脉冲,滤掉其余部分的噪声,并在0~100Hz频带范围内展开滤波(图 4),由图 4(a)可见,时频滤波后50Hz的电流噪声不再存在;图 4(b)的频谱在50Hz处出现明显的凹陷,噪声尖刺已经滤去,整体上较为平滑;图 4(c)的时域波形出现明显的气泡脉冲。
|
图 3 近场水听器记录时频分析 (a)时频谱;(b)频域记录;(c)时域波形 |

|
图 4 近场水听器记录滤波后时频分析 (a)时频谱;(b)频域记录;(c)时域波形 |
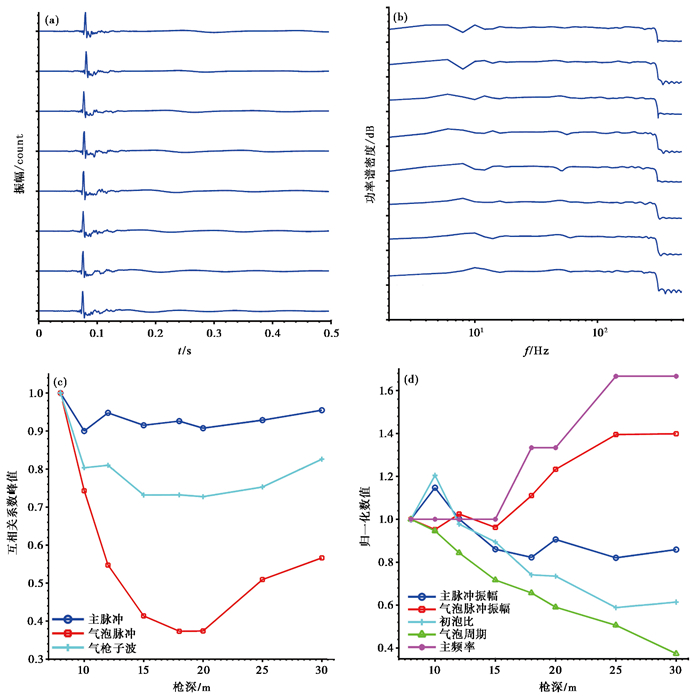
气枪沉放深度是影响气枪激发子波的关键因素之一。气枪沉放深度对静水压力和水面虚反射有直接影响,进而影响高压气体的释放速度、气泡振荡和子波波形等。为探究沉放深度对气枪激发子波的影响,在工作压力为2000psi、水深45m的工况条件下,我们对A枪做了沉放深度为8、10、12、15、18、20、25、30m的工况实验,每个工况激发9次,对每次激发波形作时频滤波后取子波参数的平均值并归一化后进行比较,表 1为不同沉放深度的气枪近场子波参数。不同沉放深度的近场水听器数据分析见图 5,图 5(a)、5(b)从上到下依次为沉放深度8、10、12、15、18、20、25、30m时A枪首次激发的近场子波波形和频谱。由图 5(a)、5(b)可见,随着沉放深度的增加,主脉冲波形较一致,气泡脉冲波形存在很大差异,气泡周期逐渐减小,低频段第1主频逐渐增加。图 5(c)为不同沉放深度下近场子波波形相关性的比较,由图 5(c)可见,主脉冲波形(0~0.1s段)互相关系数峰值为0.9002~1.0000,不同沉放深度之间相关性很高。气泡脉冲波形(0.1~0.5s段)互相关系数峰值为0.3734~1.0000,不同沉放深度之间相关性较低。气枪子波波形(0~0.5s段)互相关系数峰值为0.7273~1.0000,相关性介于主脉冲和气泡脉冲之间。图 5(d)为将子波参数归一化后进行的比较,由图 5(d)可见,随沉放深度的增加,主脉冲振幅振荡变小,但变化范围较小,归一化数值为0.82~1.15。这是由于沉放深度增大,静水压力增加,进而引起高压气体释放速度减小,主脉冲振幅减弱,波形变宽,频带变窄。由于静水压力相对于工作压力而言很小,因此,主脉冲变化幅度较小。
| 表 1 不同沉放深度的气枪近场子波参数 |
|
图 5 不同沉放深度的近场水听器数据分析 (a)时域波形;(b)频谱记录;(c)波形相关;(d)子波参数 |
气泡脉冲振幅与沉放深度密切相关,当枪深小于气泡半径时,气泡在形成的瞬间就会破裂,气泡内部气体逸出,能量发散到空气中,不会出现气泡振荡。当枪深刚好等于气泡半径时,由于气泡内部气体密度小于水的密度,在水的浮力作用下,气泡冲出水面,同样会出现气泡破裂,气体逸出,能量发散。当枪深为气泡半径的1~3倍时,形成的气泡在振荡时会引起水面的波动起伏,消耗能量,气泡振荡较弱。当枪深大于气泡半径的3倍时,气泡振荡随沉放深度的增加而增强。A枪单枪激发时,气泡半径近似为1m,气枪沉放深度从8m增加到30m,气泡脉冲振幅随沉放深度的增加总体呈递增趋势,归一化数值为0.95~1.40。随着沉放深度的增加,主脉冲振荡变小,气泡脉冲逐渐增加,初泡比振荡减小,为13.732~28.128,归一化数值为0.588~1.205。当沉放深度为10m时,主脉冲振幅最大,这与唐杰等(2009)、林建民等(2010)的研究结果是一致的。此时初泡比最大,可应用于浅部探测。而对于深部探测,可以通过增加沉放深度来加强气泡振荡效应。沉放深度为30m时,气泡脉冲振幅最大,25m时振幅与30m时接近,而初泡比最小,可应用于深部探测。
气枪沉放越深,气泡振荡能量越大,气泡振荡速度越快,气泡周期明显减小,从0.166s减小到0.062s,归一化数值从1.000减小到0.373。相应地,低频段主频从6Hz增加到10Hz,归一化数值从1.00增加到1.67,呈阶梯型增长。这是由于近场水听器采样率为1000Hz,而波形记录时长0.5s,只记录了500个点,从而导致频域分辨率较低,但也反映了低频段主频随沉放深度的增加而递增的趋势。
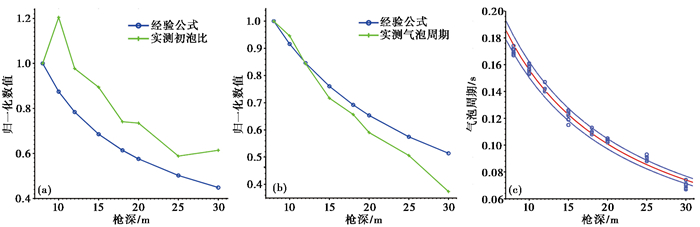
根据实验结果,将实测初泡比、气泡周期与经验公式(式(2)、(3))归一化后进行比较,可以看到,初泡比实测值在枪深10m时最大,之后随枪深的增加振荡变小,与式(2)、(3) 的变化趋势总体上一致,气泡周期的经验公式和实测值都随气枪沉放深度的增加而减小,且实测值的减小幅度更大。同时,利用实测气泡周期,拟合得到气泡周期与沉放深度的关系如下
| $ \text{lg}T=-1.0771\text{lg}\left(D+10 \right)+0.5947\pm 0.0164 $ | (4) |
| $ T=3.9328{{\left(D+10 \right)}^{-1.0771}}, 相关系数-0.9911 $ | (5) |
其中,T为气泡周期;D为气枪沉放深度。气泡周期与沉放深度的相关系数为-0.9911,这进一步说明气泡周期与沉放深度密切相关。图 6为气枪子波参数实测值与经验公式(式(2)(3))的比较和气泡周期与沉放深度的拟合。
|
图 6 气枪子波参数实测值与经验公式的比较和气泡周期与沉放深度的拟合 (a)初泡比经验公式(式(2))与实测值的比较;(b)气泡周期经验公式(式(3))与实测值的比较;(c)气泡周期与沉放深度的拟合 |
工作压力主要影响气泡内部的压力,工作压力越大,气体释放速度越快,产生的气泡子波能量越强。早期气枪的工作压力大于6000psi,工作时危险性很大,同时会对水中生物造成很大伤害,难以满足安全、环保的需求,目前通用的工作压力为2000psi。
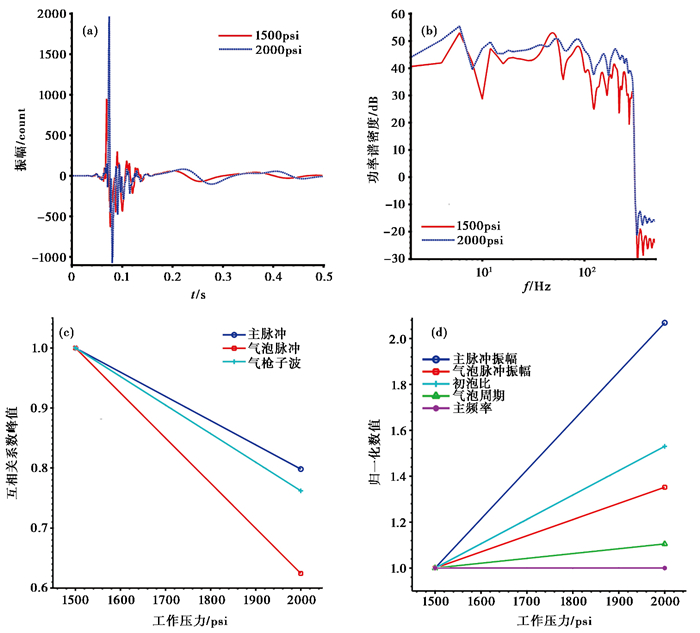
为探究工作压力对气枪激发子波的影响,在沉放深度15m、水深25m的工况条件下,我们对气枪阵列进行了工作压力为1500、2000psi的工况实验,每个工况激发9次,对每次激发波形作时频滤波后取子波参数的平均值,并归一化后进行比较,表 2为不同工作压力下的气枪近场子波参数。图 7(a)、7(b)为枪阵首次激发A枪的近场子波波形和频谱。由图 7(a)、7(b)可见,工作压力为2000psi时,主脉冲振幅、气泡脉冲振幅和气泡周期都比1500psi时的大,由于频率的分辨率不够,低频段第1主频保持一致。图 7(c)为不同工作压力下的近场子波波形相关性比较,由图 7(c)可见,主脉冲波形(0~0.1s段)互相关系数峰值为0.798~1.000,气泡脉冲波形(0.1~0.5s段)的为0.6242~1.0000,气枪子波波形(0~0.5s段)的为0.7619~1.0000。不同工作压力之间主脉冲波形的相关性高于气泡脉冲波形,气枪子波的相关性介于主脉冲和气泡脉冲之间。图 7(d)为对子波参数归一化后进行比较,由图 7(d)可见,工作压力从1500psi增加到2000psi,主脉冲振幅增加了1.07倍,气泡脉冲振幅增加了0.352倍,主脉冲振幅增加的幅度大于气泡脉冲,相应地初泡比从15.67到23.98,增加了0.53倍,气泡周期从0.133s增加到0.147s,增加了0.105倍。
| 表 2 不同工作压力的气枪近场子波参数 |
|
图 7 不同工作压力的近场水听器数据分析 (a)时域波形;(b)频谱记录;(c)波形相关;(d)子波参数 |
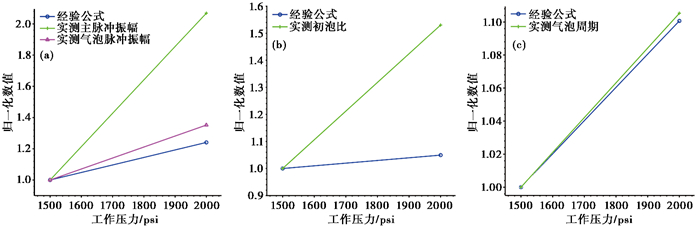
将实测子波参数与经验公式(式(1)、(2)、(3))进行比较(图 8),由图(8)可见,实测的主脉冲振幅、初泡比随工作压力增加的幅度大于经验公式,而实测的气泡脉冲振幅、气泡周期的增加幅度与经验公式较为一致。
|
图 8 不同工作压力的子波参数经验公式与实测值的比较 (a)主脉冲振幅和气泡脉冲振幅;(b)初泡比;(c)气泡周期 |
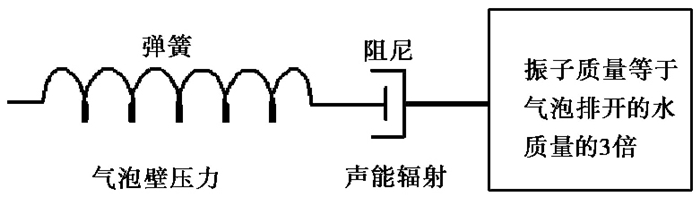
Johnson(1994)将气泡振荡过程等效为1个有阻尼的弹簧振子,用简单的物理和数学原理对气泡振荡赋予新的解释(图 9),共振水体等效为弹簧振子,气泡振荡等效为弹簧,气泡振荡过程的能量衰减等效为阻尼。振子质量为气泡排开的水质量的3倍,根据弹簧振子的自振周期公式可求得气泡周期
| $ \tau =2\text{ }\!\!\pi\!\!\text{ }{{R}_{\infty }}\sqrt{\frac{{{\rho }_{\infty }}}{3\gamma {{P}_{\infty }}}} $ | (6) |
|
图 9 气泡振荡模型(据Johnson(1994)) |
气泡内部压力满足理想气体状态方程
| $ {P_{\rm{a}}}\frac{{4{\rm{\pi }}}}{3}{R^3}\gamma = {P_\infty }\frac{{4{\rm{\pi }}}}{3}{R^3}{\gamma _\infty } = m \cdot {R_{\rm{g}}} \cdot T $ | (7) |
即
| $ {{P}_{\text{a}}}={{P}_{\infty }}{{\left(\frac{{{R}_{\infty }}}{R} \right)}^{3}}\gamma $ | (8) |
其中,ρ∞为水的密度;P∞为静水压力;Pa为气泡内部压力;R为气泡半径;R∞为气泡平衡半径;m为气泡内部空气质量;Rg为气体常数,对于空气取Rg=287J/(kg/°K);T为气泡内部温度;γ为热容比,等温条件下为1.0,绝热条件下为1.4,Ziolkowski(1970)选定γ=1.13。
将
| $ \tau =\frac{4\text{ }\!\!\pi\!\!\text{ }}{3}\sqrt{\frac{\pi \rho {{R}_{\infty }}^{3}\gamma +2}{\gamma m\text{ }\!\!\cdot\!\!\text{ }{{R}_{\text{g}}}\text{ }\!\!\cdot\!\!\text{ }T}} $ | (9) |
当气枪容量和工作压力一定时,m·Rg·T为常数,气枪沉放深度D越大,静水压力P∞越大,气泡体积V越小,则平衡半径R∞越小,由式(9) 可得,气泡周期τ随之减小,低频段主频f随之增大。气枪容量和沉放深度一定时,P∞为常数,工作压力增加,则平衡半径R∞增加,由式(6) 可得,气泡周期τ随之增大,低频段主频f随之减小。这与实测子波波形和频谱随沉放深度和工作压力的变化是一致的。
相应的气枪激发能量为
| $ \text{signature}=R\left({{P}_{\text{a}}}-{{P}_{\infty }}+\text{ }\frac{{{\rho }_{\infty }}{{{\dot{R}}}^{2}}}{2} \right) $ | (10) |
气泡运动方程为
| $ \ddot{R}=\frac{{{P}_{\text{a}}}-{{P}_{\infty }}}{{{\rho }_{\infty }}R}-\frac{3{{{\dot{R}}}^{2}}}{2R}+\frac{1}{{{\rho }_{\infty }}{{c}_{\infty }}}\frac{\text{d}P}{\text{d}t} $ | (11) |
其中,R为气泡半径;
高压气体释放到水中,被周围的水围成一个近似球形的气泡,气泡在水中不断振荡直至衰减破裂,形成一系列子波脉冲。气枪子波由主脉冲和气泡脉冲组成。主脉冲振幅大,持时短,频带宽,常用于浅部探测。气泡脉冲能量集中在低频段,垂直穿透深,水平传播远,常用于深部探测。
气枪震源子波受沉放深度和工作压力等工况参数的影响。沉放深度对静水压力和水面虚反射有直接影响,进而影响到高压气体的释放速度、气泡振荡效应、子波波形和频谱特征等。在浅部探测中,由于气泡振荡会影响信号的分辨率,因此需要增强主脉冲,压制气泡脉冲,拓宽地震信号频带。当气枪沉放深度较浅时,则气泡能量较弱,气泡周期较长,子波频谱较平滑。此时,可以同时利用气泡之间的相干、调谐作用,通过调节不同的枪阵组合来削弱气泡振荡,减小气泡脉冲振幅,从而获取平滑的宽频带,以增强浅部探测的分辨率。通过分析街面水库气枪近场水听器波形记录发现,沉放深度为10m时,主脉冲振幅和初泡比最大,可应用于浅部探测。
在深部探测中,需要增强气泡脉冲能量,增加子波低频成分,增加地震波的穿透深度和传播距离。气枪沉放越深,则气泡振荡越剧烈,子波能量越强,气泡周期越短,低频段主频也相应增加。同时,沉放越深,水面虚反射引起的陷波频率变小,震源子波的通频带变窄,中心频率向低频方向移动,对气枪子波能量会有压制作用。因此,在深部探测中,需要选择合适的沉放深度,兼顾低频和能量的需求,必要时需要通过现场实验来确定。通过分析街面水库气枪波形记录发现,沉放深度为25m时,初泡比最大,可应用于深部探测。
工作压力主要影响气泡内部压力。工作压力越大,气体释放速度越快,产生的气泡子波能量越强。随着工作压力的增加,主脉冲振幅增加的幅度大于气泡脉冲,初泡比和气泡周期也相应增加。
通过研究气枪子波时频特性及其受沉放深度、工作压力等的影响情况,有助于我们根据不同探测目标对震源激发信号的不同需求,调整激发参数,选择最优工况,获取最佳激发效果。
| 何汉漪. 2001, 海上高分辨率地震技术及其应用. 北京: 地质出版社: 1-129. |
| 林建民, 2008, 基于人工震源的长偏移距地震信号检测和探测研究, 博士论文, 合肥: 中国科学技术大学. |
| 林建民, 王宝善, 葛洪魁, 等. 2010, 大容量气枪震源子波激发特性分析. 地球物理学报, 53(2): 342–349. |
| 罗桂纯, 王宝善, 葛洪魁, 等. 2006, 气枪震源在地球深部结构探测中的应用研究进展. 地球物理学进展, 21(2): 400–407. |
| 丘学林, 赵明辉, 叶春明, 等. 2003, 南海东北部海陆联测与海底地震仪探测. 大地构造与成矿学, 27(4): 295–300. |
| 唐杰, 2008, 区域尺度深部探测中的人工源震源特性及信号检测研究, 博士论文, 合肥: 中国科学技术大学. |
| 唐杰, 王宝善, 葛洪魁, 等. 2009, 大容量气枪震源的实验与模拟研究. 中国地震, 25(1): 1–10. |
| 王宝善, 王伟涛, 葛洪魁, 等. 2011, 人工震源地下介质变化动态监测. 地球科学进展, 26(3): 249–256. |
| 王宝善、杨微、王伟涛等, 2013, 利用大容量气枪监测北天山地壳介质变化, 见: 中国地球物理学会, 中国地球物理2013——第十二专题论文集, 2, 北京: 中国学术期刊(光盘版)电子杂志社. |
| 王伟涛, 2009, 基于人工震源的区域尺度介质波速探测研究, 博士论文, 合肥: 中国科学技术大学. |
| 杨微, 2013, 区域尺度主动源探测技术及试验研究, 博士论文, 北京: 中国地震局地球物理研究所. |
| 杨微, 王宝善, 葛洪魁, 等. 2013, 大容量气枪震源主动探测技术系统及试验研究. 中国地震, 29(4): 399–410. |
| Brenguier F, Campillo M, Hadziioannou C, et al. 2008, Postseismic relaxation along the San Andreas Fault at Parkfield from continuous seismological observations. Science, 321: 1478–1481. DOI:10.1126/science.1160943. |
| Johnson D T. 1994, Understanding air-gun bubble behavior. Geophysics, 59(11): 1729–1734. DOI:10.1190/1.1443559. |
| Okaya D A, Henrys S, Stem T. 2002, Double sided onshore-offshore seismic imaging of a plate boundary:"super-gathers"across South Island, New Zealand. Tectonophysics, 355(2002): 247–263. |
| Woods H, 1995, Los Angeles region seismic experiment(LARSE)-cruise report. |
| Ziolkowski A. 1970, A method for calculating the output pressure waveform from an air-gun. Geophys J Roy Astr Soc, 21: 137–161. DOI:10.1111/j.1365-246X.1970.tb01773.x. |
 2016, Vol. 32
2016, Vol. 32


