2. 中国科学院地质与地球物理研究所, 北京市北土城西路19号 100029;
3. 中国海洋大学工程学院, 青岛 266100;
4. 西安近代化学研究所, 西安 710065;
5. 云南省地震局, 昆明 650224
2. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
3. College of Engineering, Ocean University of China, Qingdao 266100, Shandong, China;
4. Xi'an Modern Chemistry Research Institute, Xi'an 710065, China;
5. Earthquake Administration of Yunnan Province, Kunming 650224, China
主动源探测的目的是构建“地下云图”,也称为“地下明灯研究计划”(陈颙等,2005;王宝善等,2011;王彬等,2015)。进行区域尺度地下结构的探测监测,既是了解地震发生的物理过程、减轻地震灾害的需要,也是我们汲取自然资源、保障自身安全的需要。气枪震源具有频率低、传播距离远、重复性好、对环境无破坏等特点,非常适合区域尺度地下结构的探测监测,在海上石油勘探和海陆联测等方面已得到广泛的应用。
在气枪的理论研究方面,美国Keller等(1956)在流体可压缩性的基础上,以炸药激发的气泡为研究对象,解决了可压缩流体假设下的气泡振荡问题,计算结果与实际爆破数据非常接近,成为后来用于气枪研制、使用的齐奥科斯基模型(Ziolkowski,1970)、舒尔兹-盖特曼模型(Schulze,1972)和萨法模型(Safar,1976)的理论基础。Ziolkowski等(1982)、Parkes等(1984)利用近场水听器的测量信号来计算远场信号,美国PGS公司据此开发出了Nucleus气枪阵列子波模拟软件,该软件目前在气枪阵列优选等方面使用较普遍,有力地促进了海上气枪阵列的大量使用。陈浩林等(2002、2003、2005、2008) 对齐奥科斯基模型、舒尔兹-盖特曼模型作了修正,对单枪子波、相干枪和单枪组成的气枪阵列子波进行了数值模拟,也进行了基于近场测量的气枪阵列远场子波数值模拟工作。李绪宣等(2008、2012)、杨凯等(2011)、王建花等(2012)使用Nucleus软件进行了海上多子阵立体阵的理论和实验研究,结果表明,立体阵列能够压制海面虚反射引起的陷波作用,主脉冲和初泡比大,有效频带宽。近50多年来,大多数气枪子波特性模拟都是采用一维模型进行计算。King等(2015b)考虑反射波与气泡间的相互作用,采用有限体积法进行了二维模拟,计算了反射信号对近场信号、气泡形状等的影响,研究认为,气泡位置越深,反射波的影响越小。King(2015a)通过实验测试和理论计算进行了气枪激发的水面反射波对气泡影响的研究,指出需要三维仿真来进行更深入的研究。
近年来,在陆地上开始采用大容量非调制气枪阵列作为人工震源(杨微,2013;Monika,2014;陈蒙,2014;Kjetil et al,2015;刘自凤等,2015)。水中高压气泡的运动规律即是其中热门的研究领域(汪斌等,2008;张阿漫等,2008;贾宪振等,2015)。目前,有关水中气泡脉动方面的研究大多是以炸药的水中爆炸为背景,主要用于水中兵器爆炸威力评估和舰艇结构的抗爆设计,而水中气泡脉动在地震领域的应用研究还很少见。水中炸药爆炸具有一定的破坏性且污染水源,不宜作为水中震源。而气枪在水中产生的气泡强度可控、无污染,是水中震源的较好选择。本文结合气枪的工作过程特性,采用水中的三维高压气泡模拟单支气枪的激发过程,研究水中三维气泡的脉动规律,以期为主动源探测的气枪震源理论研究、优化使用以及水中结构的抗震防护等提供参考。
1 气枪激发过程计算模型的简化水中激发气枪产生地震波的过程是将压缩空气注入水下的气枪中,通过电磁阀将高压气体瞬间释放到水里,形成一个近似球形的气泡,由于刚开始形成的气泡内部的压力远大于周围水体的静水压,气泡迅速膨胀产生冲击波,之后气泡不断膨胀,气泡内的压力不断减小,直到气泡内的压力与静水压相等。此时,由于惯性作用,气泡依然会继续增大,但是增大的速度会越来越小,达到临界状态后气泡不再增大。在周围水体压力的作用下,气泡又开始收缩,达到临界状态后气泡不再收缩。此时,气泡内的压力又远大于周围水体的压力,气泡再次膨胀。如此往复,产生气泡脉动,直至由于摩擦等原因能量耗尽。冲击波和高压气泡的脉动压力波均可引起水底等产生振动,冲击波频率较高,气泡的脉动压力波频率较低。气枪用作陆地区域尺度地下结构探测监测的主动震源时,由于高频信号易衰减,若要在远处接收到气枪信号并进行垂直穿透深、水平传播距离远的深部探测,则需气枪激发出频率低、能量大的气泡脉动压力波,即主要由高压气泡的脉动压力波来产生远距离传播的地震波。因此,为了研究气枪的水下近场特性,将气枪的水下激发过程简化为脉动的高压气泡更便于三维数值模拟并节约计算时间。
气泡脉动对水介质的作用是一个低压、长时间的过程(汪斌等,2008),故可将水当作不可压缩流体处理。假定气泡只产生径向运动而无垂直位移,则可忽略水黏性和热传导条件。假设气泡内气体平均压力为Pb,气泡内气体的绝热指数为k,R0为气泡的初始半径,那么在水深压力为P0、水密度为ρ0的条件下,一维球对称气泡半径R随时间t变化的二阶非线性微分方程为
| $ R\frac{{{{\rm{d}}^{\rm{2}}}R}}{{{\rm{d}}{t^{\rm{2}}}}} + \frac{3}{2}{\left({\frac{{{\rm{d}}R}}{{{\rm{d}}t}}} \right)^2} = \frac{1}{{{\rho _0}R}}\left[ {{P_{\rm{b}}}{{\left({\frac{{{R_0}}}{R}} \right)}^{3k}} - {P_0}} \right] $ | (1) |
由式(1) 可得气泡膨胀过程的解析解为
| $ \frac{{{\rm{d}}R}}{{{\rm{d}}t}} = \sqrt {\frac{2}{3}\frac{1}{{{\rho _0}}}{{\left({\frac{{{R_0}}}{R}} \right)}^3}\left\{ {\frac{{{P_{\rm{b}}}}}{{k - 1}}\left[ {1 - {{\left({\frac{{{R_0}}}{R}} \right)}^{3(k - 1)}}} \right] + \left[ {1 - {{\left({\frac{{{R_0}}}{R}} \right)}^3}} \right]} \right\}{P_0}} $ | (2) |
由式(2) 可以看出,在初始时刻气泡膨胀速度等于0;随着气泡半径的增大,速度迅速增加到最大值,然后缓慢下降;当气泡膨胀到最大值时,速度降为0。
2 气枪气泡脉动的计算模型气枪阀门打开期间形成的气泡可考虑为一个球形的水中高压气泡,由于高压气泡的压力远远大于周围的静水压力,所以必然压缩周围水介质产生冲击波,同时气泡发生膨胀而产生水中脉动现象。高压气泡的运动过程十分复杂,涉及到流体动力学、流体热力学、流固耦合等方面。为简化分析,在建立计算模型时作以下假设:① 初始时刻流场处于静止状态,流体各质点速度均为0;② 流场是无旋、无粘的;③ 高压气泡的组分为空气;④ 高压气泡与水介质之间没有热交换,即气泡的运动过程是绝热的;⑤ 不考虑气泡在竖直方向的运动,只考虑气泡的膨胀、收缩运动。
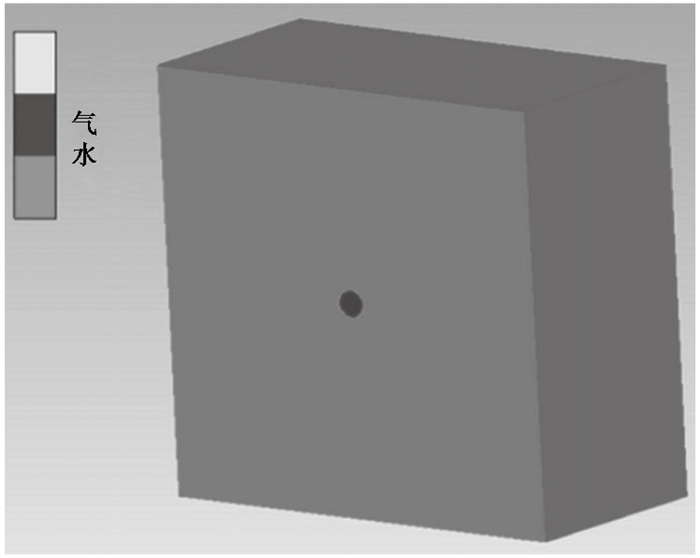
根据主动源探测过程中使用气枪时的普通工况条件,在ANSYS AUTODYN程序中建立三维计算模型(图 1)。计算模型包含水和高压气泡2种组分,高压气泡呈球形,初始直径为1.2m,初始压力为10MPa。在气泡中心设置测点以记录气泡中心的压力变化,在距气泡中心2m处设置测点以记录气泡脉动导致的水中压力的变化。
|
图 1 三维计算模型示意图 |
为了研究气枪震源激发的气泡脉动压力的频率成分和压力随沉放深度的变化规律,按照气泡中心所处深度的不同分为5种工况(表 1),对应的深度分别为10、20、30、40、50m,各工况的气泡直径和初始压力均相同。
| 表 1 计算工况 |
空间离散域的描述选择Euler方法,该方法中网格点固定不变,材料在网格中流动,能够有效避免网格变形所带来的网格畸变和时间步长变小等问题,故适用于流体问题的数值模拟。关于边界条件,为了模拟无限大流场,在流场边界处均设置了流出条件,这样可以使冲击波在流场边界处不发生反射而直接流出,不会对后续的气泡运动产生影响。在状态方程方面,高压气泡采用理想气体状态方程
| $ P = (\gamma - 1)\rho {e_0} $ | (3) |
式中,e0为气泡的初始比内能,通过不同的e0值可以模拟不同的气泡压力;ρ为密度;γ为绝热指数,气枪内部气体为压缩空气,故γ取1.4。
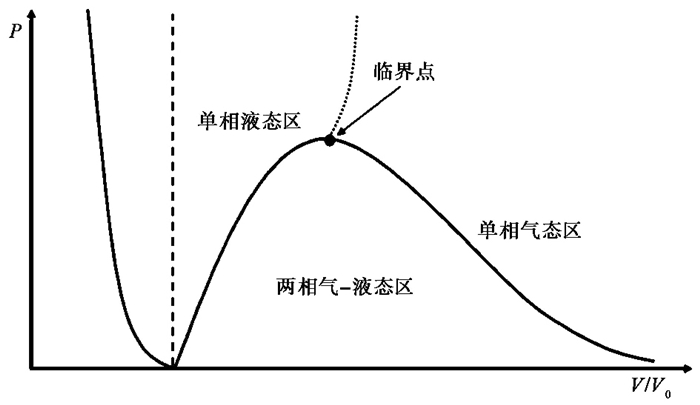
水的状态方程采用两相状态方程(ANSYS Corporation,2005)。高压气泡初始时刻强烈压缩周围的水,此时位于气泡附近的水在某一时刻、某一区域可能是气态、液态或气液混合状态。两相状态方程既可描述水或水蒸气的单一状态,也可描述水和水蒸气共存的状态。图 2给出了(P,V)平面图,图中曲线为饱和曲线,曲线上方为只有气态或液态的单一态,曲线下方为气液共存状态。
|
图 2 (P,V)平面上的各区域 |
对于只存在水或水蒸气的单一态,状态方程采用Gruneisen方程(ANSYS Corporation,2005)
| $ P = {P_{\rm{r}}}(V) + \frac{{\mathit{\Gamma} (V)}}{V}\left[ {E - {E_{\rm{r}}}(V)} \right] $ | (4) |
式中,P、V、E分别为流体的压强、体积和单位体积的内能;Pr和Er分别为压强和内能在饱和曲线上的值。在图 2的饱和曲线下方区域水和水蒸气共存,则
| $ V = \alpha {V_{\rm{g}}} + (1 - \alpha){V_1} $ | (5) |
| $ E = \alpha {E_{\rm{g}}} + (1 - \alpha){E_1} $ | (6) |
式中,α为单位体积内水蒸气的质量分数;Vg、V1、Eg、E1分别为水蒸气达到饱和状态时单位体积内水蒸气、水的体积和内能。由式(5)、(6)得
| $ \frac{{(V - {V_{\rm{g}}})}}{{({V_{\rm{g}}} - {V_1})}} = \frac{{(E - {E_{\rm{g}}})}}{{{E_{\rm{g}}} - {E_1})}} $ | (7) |
由式(7) 可求得V,再由饱和曲线上压力与体积的关系即可求得压力P。
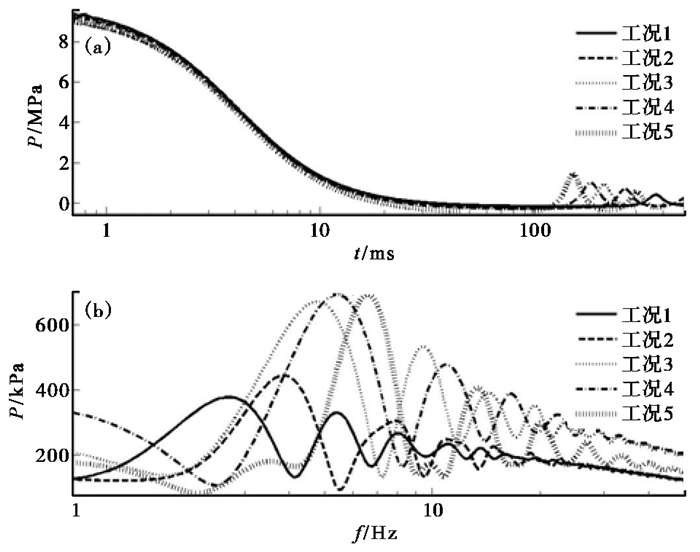
3 结果与讨论 3.1 水深的影响图 3给出了不同深度时气泡中心点的压力曲线和频谱分析结果。由图 3(a)工况1的压力曲线可见,从0时刻开始,高压气泡的压力从初始的10MPa迅速减小,到100ms时已经接近最低值,说明此时气泡在不断膨胀,其内部压力越来越小;随后到接近300ms时,压力又开始上升,至370ms时压力达到较大值,表明气泡已经压缩至最小;气泡最大压力为初始时刻的10MPa,随后脉动压力逐渐减小直至能量耗尽。由图 3(b)可知,工况1气泡在10m水深时的脉动频率为2.7Hz,脉动压力为378kPa。从图 3(b)其余工况时气泡中心点的压力曲线可以看出,随着气泡所处深度的增加,气泡脉动的周期越来越短,即脉动压力波出现的越来越早,脉动频率越来越大,同时脉动压力波的压力越来越大(表 2)。由于气泡脉动压力曲线是短时非稳态信号,故本文的频谱分析结果仅适用于气泡脉动规律的研究。
|
图 3 多种工况的气泡中心点压力曲线(a)及频谱分析(b) |
| 表 2 不同深度时气泡中心点的脉动参数 |
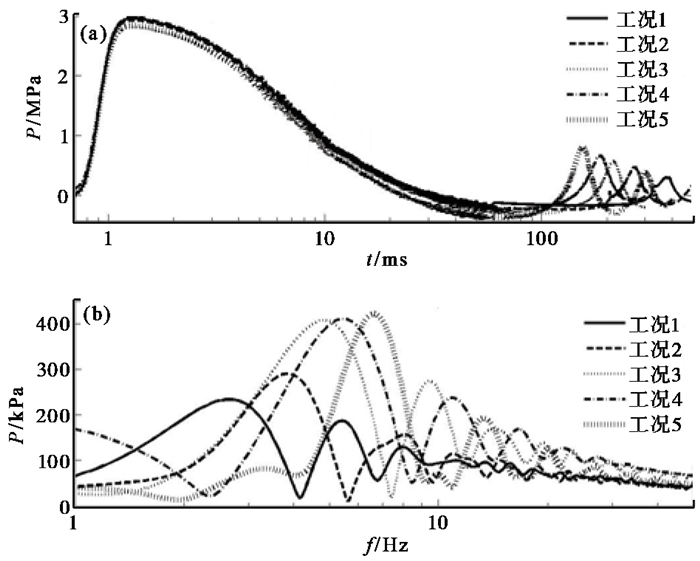
以上给出了气泡内部的压力变化情况,下面给出气泡外部水中的压力情况,以距气泡中心点2m作为观测点。图 4给出了气泡多种工况时观测点处的压力曲线和频谱分析结果,从图 4(a)工况1的压力曲线可以清晰地看到,该点首先传播1个冲击波,冲击波峰值压力约为2.9MPa,后续又有1个脉动压力波,脉动频率为2.6Hz,脉动压力为234kPa。与图 3(a)相比,此时的脉动压力波形状不规则,在上升段有凸起,这可能是由于压力流出边界条件具有近似性,在边界处还是存在一定的压力反射,反射的压力波对后续的气泡膨胀和收缩有一定的影响,导致2次压力波略有变形,不再是对称的形状。从图 4(b)多种工况的压力曲线可看出随着深度的增加,水中相同距离处的冲击波峰值压力仅略有升高,但脉动压力波的压力显著增大,且波形越来越尖,频率越来越大,该模拟结果与林建民等(2010)的气泡压力和周期随深度变化的实验结果相一致,并且该模拟结果也表明,外部脉动压力变化与气泡中心点脉动压力变化遵循同样的规律。随着水域范围的不断扩大,流出边界条件近似性的影响也越来越小,脉动压力波的波形也基本呈对称形态。上述分析表明,本文的三维计算模型以及模拟过程基本正确,可用于更复杂的气枪激发工况的理论模拟。
|
图 4 多种工况水中观测点处的压力曲线(a)及频谱分析(b) |
由表 2、3可见,随着气枪沉放深度的增加,气泡脉动压力波频率持续增大,而气泡脉动压力增大的幅度却越来越小,这一方面是由于频率越高,传播衰减越大;另一方面是由于深度增加的同时水压增大,而若气枪的喷射压力不变的话,水压与气枪喷射产生的气泡的压力差也越小,气泡脉动幅度则会受影响。以上表明气枪脉动压力与沉放深度间不是单一的递增关系,而是有一个最佳沉放深度,并非越深越好。
| 表 3 不同深度时观测点处的脉动参数 |
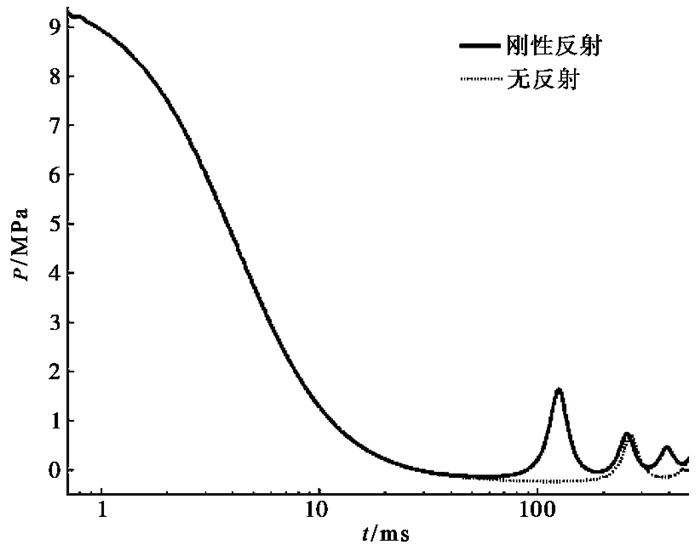
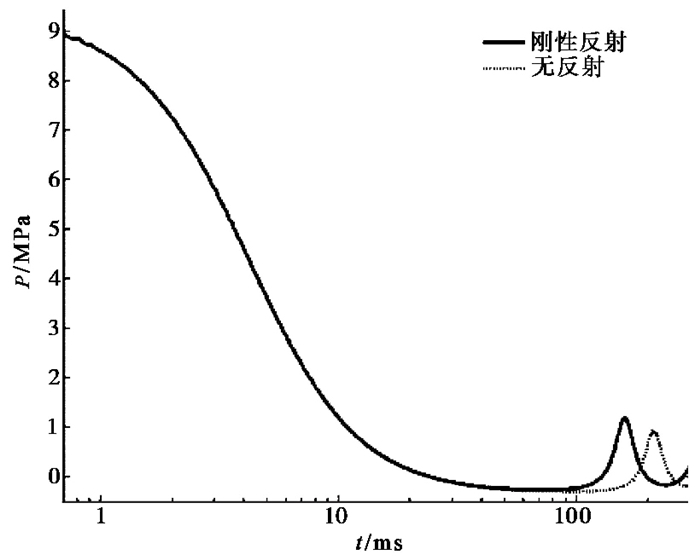
前述模拟的是气枪在无限大水体里的激发过程,为了分析气枪在有限水体里的激发过程,进一步研究了计算模型的边界全部为刚性反射边界时对计算结果的影响。对此仅在工况2、3的基础上进行研究,此时模型不再施加流出边界,而将边界设置为刚性反射边界,计算得到的气泡中心压力分别如图 5、6所示,同时引入相应的无反射边界时的计算结果以方便对比。由图 5、6可见,在刚性反射边界情况下,气泡脉动的周期减小,频率增大,气泡脉动压力波峰值增大,表明如果气枪在一个全封闭、尺寸较大的水体里,将产生强度更大的地震波。对于前述的气泡脉动压力随沉放深度增加而增加的现象,一个解释就是随着深度的增加,气枪上方的水体越来越接近刚性反射边界。在气枪不同深度的激发实验中,气枪越深,水面越平静,越看不到冒起的水泡。
|
图 5 工况2气泡中心压力曲线 |
|
图 6 工况3气泡中心压力曲线 |
气枪在实际应用时通常选择水池、水井、天然湖泊、海洋等有限水域,其水底边界可视为刚性反射边界。前述的研究表明,气枪越深,气泡脉动压力越大,那么当接近水底时,气泡脉动压力是否还会继续增大?为了研究此问题,对无反射的工况2进行计算,其余计算条件保持一致,区别仅在于在距气泡下方1m处增加了水底,气泡中心点到水底的距离为1.6m,水底为刚性反射边界。
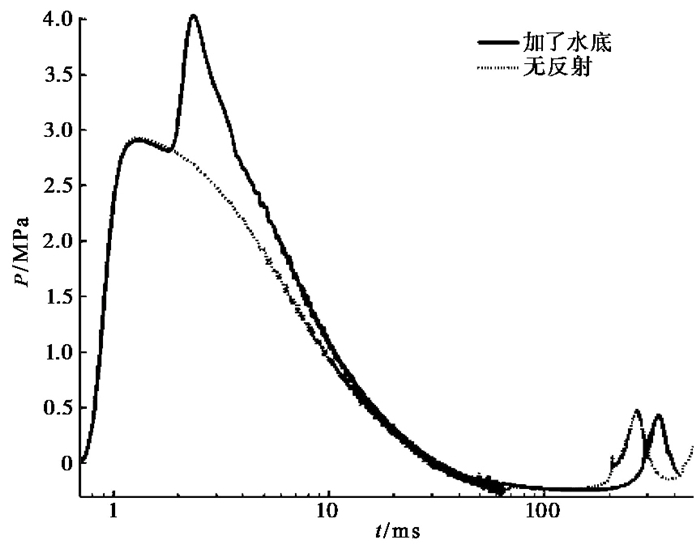
在距气泡中心点2m的相同深度处设置观测点以记录压力曲线。计算得到的压力曲线与无反射工况的对比如图 7所示。由图 7增加了水底的压力曲线可明显看出水底反射的影响,即2.904MPa的冲击波峰值过后,加了水底的冲击波出现了4.033MPa的强反射波,气泡脉动压力峰值为0.433MPa;而无反射的工况2的气泡脉动压力峰值为0.476kPa,说明水底的存在使气泡脉动压力峰值降低了。该模拟结果与主动源项目组在较小尺寸的井中开展气枪激发实验效果不理想(引起的地震波反而小)相符合。另外,水底使气泡脉动的周期增大,即频率减小。
|
图 7 工况2水中观测点处的压力曲线 |
在ANSYS AUTODYN程序中建立了水中高压气泡脉动的三维计算模型,并对不同沉放深度、边界条件的高压气泡运动规律进行了计算,得到以下主要结论:
(1) 高压气泡在水中会激发冲击波,同时产生周期性的膨胀、收缩现象,在水中产生脉动压力波。
(2) 随着气泡所处深度的增加,气泡脉动周期逐渐减小,频率变大,气泡脉动压力也逐渐增大,但压力增加的幅度逐渐减小。
(3) 与无限水域相比,在尺寸较大的刚性边界有限水域中气泡脉动周期会缩短,频率增大,脉动压力变大。
(4) 在接近水底时,气泡脉动周期增大,频率减小,脉动压力变小。
(5) 本文的三维计算模型能计算出模拟单支气枪的高压气泡的运动规律,可用于研究不同边界条件下单支气枪在水中产生的高压气泡的脉动规律,进而可用于研究多种影响因素、更复杂边界条件下平面和立体气枪阵列产生的高压气泡的脉动规律,为陆地、海洋的单支气枪、气枪阵列的优化使用提供技术支持,也可以为船体、潜艇等水中结构对于炸药或者气枪引起的水下振动的抗震防护等应用提供参考。
对提高气枪主动源激发地震波强度的建议:
(1) 气枪沉放越深,气泡脉动压力越大,但压力增大的幅度减小,同时频率也越大。水中压力脉动的频率越大,产生的地震波效率越低,因此沉放深度要适度,不能无限深。
(2) 接近类似水底刚性反射边界时,气泡脉动压力会减小,所以气枪不能离水底、井壁等边界太近。
(3) 可考虑在较大尺寸且被刚性边界封闭的水池中激发气枪,这样会产生更大强度的地震波。
| 陈浩林, 倪成洲, 邢筱君, 等. 2008, 气枪阵列远场子波模拟与应用. 石油地球物理勘探, 43(6): 623–625. |
| 陈浩林, 宁书年, 熊金良, 等. 2003, 气枪阵列子波数值模拟. 石油地球物理勘探, 38(4): 363–368. |
| 陈浩林, 全海燕, 刘军, 等. 2005, 基于近场测量的气枪阵列模拟远场子波. 石油地球物理勘探, 40(6): 703–707. |
| 陈浩林, 於国平. 2002, 气枪震源单枪子波计算机模拟. 物探装备, 12(4): 241–244. |
| 陈蒙, 2014, 利用水库大容量非调制气枪阵列进行区域尺度地下结构探测和监测, 博士论文, 北京: 中国地震局地球物理所. |
| 陈颙, 朱日祥. 2005, 设立"地下明灯研究计划"的建议. 地球科学进展, 20(5): 485–489. |
| 贾宪振, 南海, 王晓峰, 等. 2015, 有氧化剂(AP)含铝炸药水中爆炸数值模拟. 科学技术与工程, 15(6): 1–4. |
| 李绪宣, 王建花, 杨凯, 等. 2012, 海上深水区气枪震源阵列优化组合研究与应用. 中国海上油气, 24(3): 1–6. |
| 李绪宣, 温书亮, 顾汉明, 等. 2008, 海上气枪阵列震源子波数值模拟研究. 中国海上油气, 21(4): 215–220. |
| 林建民, 王宝善, 葛洪魁, 等. 2010, 大容量气枪震源子波激发特性分析. 地球物理学报, 53(2): 342–349. |
| 刘自凤, 苏有锦, 王宝善, 等. 2015, 宾川主动源地震波走时变化分析方法研究. 地震研究, 38(4): 591–598. |
| 汪斌, 张远平, 王彦平. 2008, 水中爆炸气泡脉动现象的实验研究. 爆炸与冲击, 28(6): 572–576. DOI:10.11883/1001-1455(2008)06-0572-05 |
| 王宝善, 王伟涛, 葛洪魁, 等. 2011, 人工震源地下介质变化动态监测. 地球科学进展, 26(3): 249–256. |
| 王彬, 吴国华, 苏有锦, 等. 2015, 宾川地震信号发射台的选址, 建设及初步观测结果. 地震研究, 38(1): 1–6. |
| 王建花, 李绪宣, 顾汉明, 等. 2012, 海上多子阵立体组合气枪震源优化设计. 地质科技情报, 31(2): 133–138. |
| 杨凯, 陈华, 顾汉明, 等. 2011, 深水立体延迟激发气枪震源的设计与应用. 石油地球物理学报, 8(6): 641–647. |
| 杨微, 2013, 区域尺度主动源探测技术及试验研究, 博士论文, 北京: 中国地震局地球物理研究所. |
| 张阿漫, 姚熊亮. 2008, 近边界三维水下爆炸气泡动态特性研究. 爆炸与冲击, 28(2): 124–130. DOI:10.11883/1001-1455(2008)02-0124-07 |
| ANSYS Corporation, 2005, ANSYS AUTODYN theory manual, version 6.1, United States. |
| Keller J B, Ignace I K. 1956, Damping of underwater explosion bubble oscillations. J Appl Phys, 27(10): 1152–1161. DOI:10.1063/1.1722221. |
| King J R C. 2015a, Air-gun bubble-ghost interactions. Geophysics, 80(6): T223–T234. DOI:10.1190/geo2015-0143.1. |
| King J R C, Ziolkowski A M, Ruffert M. 2015b, Boundary conditions for simulations of oscillating bubbles using the non-linear acoustic approximation. Journal of Computational Physics, 284: 273–290. DOI:10.1016/j.jcp.2014.12.037. |
| Kjetil E H, Martin L. 2015, Variable source depth acquisition for improved marine broadband seismic data. Geophysics, 80(3): A69–A73. DOI:10.1190/geo2014-0437.1. |
| Monika B. 2014, Overview of seismic research activities in the Southern Ocean-quantifying the environmental impact. Antarctic Science, 26(1): 80–92. DOI:10.1017/S095410201300031X. |
| Parkes G E, Ziolkowski A, Hatton L, et al. 1984, The signature of an air gun array:computation from near-field measurements including interactions-Practical considerations. Geophysics, 48(2): 105–111. |
| Safar M H. 1976, The radiation of acoustic waves from an air-gun. Geophysical Prospecting, 24(4): 756–772. DOI:10.1111/gpr.1976.24.issue-4. |
| Schulze G R. 1972, Physical aspects of the "airpulser" as a seismic source. Geophysical Prospecting, 20(1): 155–192. DOI:10.1111/gpr.1972.20.issue-1. |
| Ziolkowski A. 1970, A method for calculating the output pressure waveform from an air gun. Geophys J R Astr Soc, 21(2): 137–161. DOI:10.1111/j.1365-246X.1970.tb01773.x. |
| Ziolkowski A, Parkes G E, Hatton L, et al. 1982, The signature of an air-gun array:Computation from near-field measurements including interactions. Geophysics, 47(10): 1413–1421. DOI:10.1190/1.1441289. |
 2016, Vol. 32
2016, Vol. 32


