2. 中国地震局滇西地震预报实验场办公室, 云南大理 671000
2. Western Yunnan Earthquake Prediction Study Area, CEA, Dali 671000, Yunnan, China
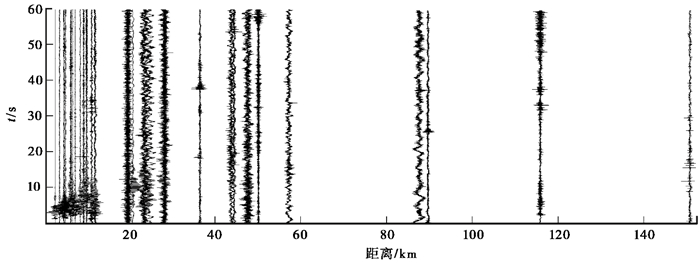
对可重复的气枪激发观测是近年地震系统探索研究的重要工作之一,它在可重复、持续、环保、精细探测地壳介质性质的动态变化等方面具有一定优势,可弥补天然地震的不足,可为地震预测研究提供新的途径和方法(陈颙等,2005、2007;王彬等,2015)。但气枪震源激发能量较弱,传播距离有限,由于衰减的原因震源信号在到达一定距离的接收台站之后会变得非常微弱,信噪比变低,有效信号难以识别(图 1)。然而由于气枪震源及接收台站的位置固定,持续激发的信号具有较高的相似性和很好的重复性,因此将台站接收到的气枪重复激发的多个信号进行叠加是提高信噪比的有效手段(苑益军等,2005),也是在强背景随机噪声下提取弱信号的主要方法。
|
图 1 宾川气枪震源发射台不同震中距垂向原始记录的时-距曲线 |
提取高度重复记录中的弱信号,一般采用线性直接叠加方法,其结果并不改变信号的原有形态,但提取弱信号的能力有限(Schimmel,1999;苑益军等,2005)。为了进一步提高强背景噪声下弱信号的提取能力,Schimmel等(1997)研究了相位互相关技术并将其应用于地震波形信号处理中,在实际叠加时引入相位加权技术,它能够有效地压制尖锐噪声、突出有效的地震信号。为了更充分地利用相位信息,Schimmel等(2011)基于S变换提出了S变换叠加方法用于地震弱信号的提取。其它研究者也开展了类似工作,提出了不同的叠加方法(苑益军等,2005)。
为了深入探究上述叠加方法处理气枪震源信号的实际性能,更好地选择观测波形的叠加模式,本文通过数值合成仿真和气枪震源信号处理,系统探讨这些叠加方法提取气枪震源弱信号的实际能力、效率和可靠性等问题,以便有针对性地选用叠加方法,更加有效、基本保真地在强背景噪声中提取气枪震源重复激发的弱信号。
1 线性/相位加权/S变换叠加方法简介 1.1 线性叠加原理将人工震源重复激发信号、台站同时接收到的若干条记录进行激发时间对齐后直接叠加,然后求平均,即为简单的时域叠加方法,也称为线性直接叠加方法。其叠加公式为(牟永光,1986)
| $ X\left( t \right) = \frac{1}{N}\sum\limits_{j = 1}^N {{x_j}\left( t \right)} $ | (1) |
式中,X(t)为叠加输出结果;xj (t)为第j枪的时间记录;N为记录数。
1.2 相位加权叠加原理相位加权叠加方法是一种非线性叠加技术,通过叠加能够有效去除不相干的噪声,增强相干性的信号(Schimmel et al,1997)。用记录x(t)及其Hilbert变换H[x(t)]构造复数序列X(t),即
| $ X\left(t \right) = x\left(t \right) + iH\left[ {x\left(t \right)} \right] = A\left(t \right){{\rm{e}}^{i\varphi (t)}} $ | (2) |
其中,A(t)为X(t)的振幅;φ(t)为瞬时相位。相位加权叠加N条不同的记录x(t)时,利用瞬时相位φ(t)采用如下叠加权重规则
| $ x\left(t \right) = \frac{1}{N}\sum\limits_{j = 1}^N {{x_j}} \left(t \right){\left| {\frac{1}{N}\sum\limits_{j = 1}^N {{{\rm{e}}^{i{\varphi _j}\left(t \right)}}} } \right|^\upsilon } $ | (3) |
其中,υ为指数。
1.3 S变换叠加原理S变换的核心公式为(Stoekwell et al,1996)
| $ S\left({\tau, f} \right) = \smallint \mu \left(t \right)\omega \left({\tau - t, f} \right){{\rm{e}}^{ - i2\pi ft}}{\rm{d}}t $ | (4) |
其中,f为频率;t为时间;τ为窗函数的中心;ω(τ-t,f)为在τ时间宽度与|1/f|成比例的高斯窗函数,其具体形式为
| $ \omega \left({\tau - t, f} \right) = \frac{{|f|}}{{k\sqrt {2\pi } }}{{\rm{e}}^{\frac{{ - {f^2}{{\left({\tau - t} \right)}^2}}}{{2{k^2}}}}} $ | (5) |
其中,k为高斯窗函数的控制参量,k>0。
在时频域S(τ,f)的相位权重为(Schimmel et al,2011)
| $ {C_{{\rm{ps}}}}\left( {\tau ,f} \right) = {\left| {\frac{1}{N}\sum\limits_{j = 1}^N {\frac{{{S_j}\left( {\tau ,f} \right){{\rm{e}}^{i2\pi \tau t}}}}{{|{S_j}\left( {\tau ,f} \right)|}}} } \right|^\upsilon } $ | (6) |
时频域的叠加形式则为(Schimmel et al,2011)
| $ {S_{{\rm{pws}}}}\left({\tau, f} \right) = {C_{{\rm{ps}}}}\left({\tau, f} \right){S_{{\rm{ls}}}}\left({\tau, f} \right) $ | (7) |
即时频域的相位加权叠加结果为相位相关与所有时间域数据线性叠加后做S变换的乘积,最后再反变换到时间域,最终获得S变换叠加结果。
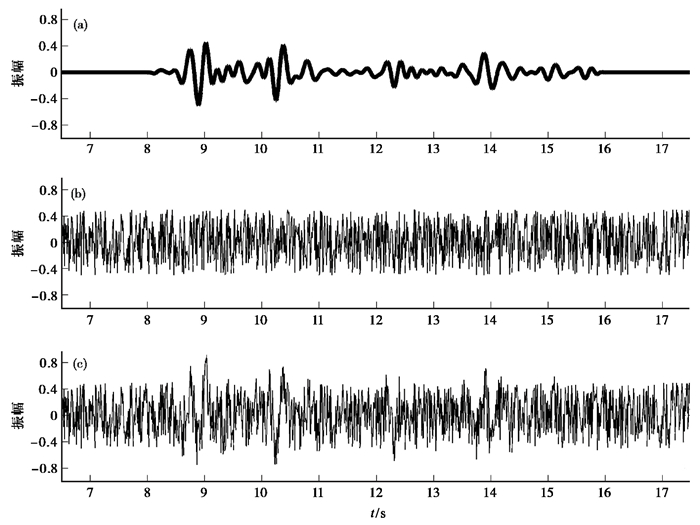
2 噪声背景下弱信号提取的可靠性仿真 2.1 仿真数据的合成方法与弱信号提取的可靠性评估方案首先,产生20s时长、采样间隔0.01s的0值时间序列,然后截取采样率100Hz、长度8s的天然地震波形作为独立对比的参考信号,将其插入到0值时间序列的10~18s之间,数值范围归一化为[-0.5,+0.5],其它时间段数值仍保持为0(图 2(a));然后,再利用均匀随机发生器(杨华中等,1996)产生等幅、等采样间隔、等持续时长的随机时间序列(图 2(b)),将其与参考信号叠加,最终合成为带有噪声的弱信号模板波形时间序列(图 2(c)),结果相当于1条完整的包含强噪声背景的弱信号记录,至此完成仿真试验数据的合成。依此,在每次叠加时都动态产生随机噪声序列与独立的参考信号序列,实时合成参与叠加的波形时间序列。
|
图 2 已知参考波形(a)、均匀随机数生成时间序列(b)及合成模板波形(c)记录 |
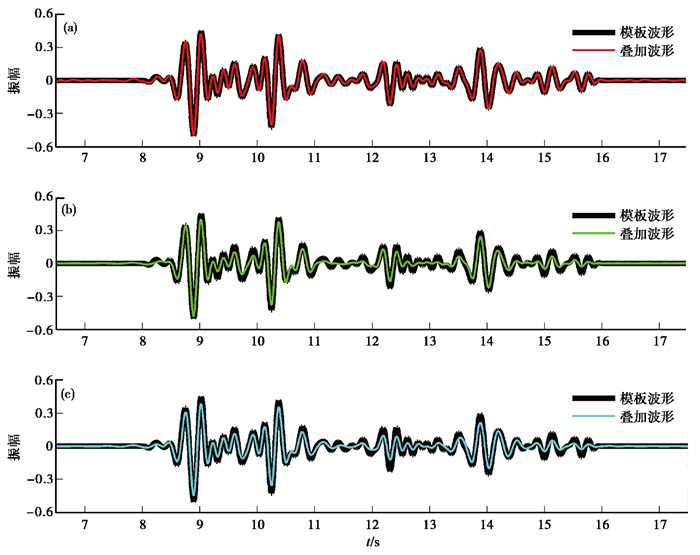
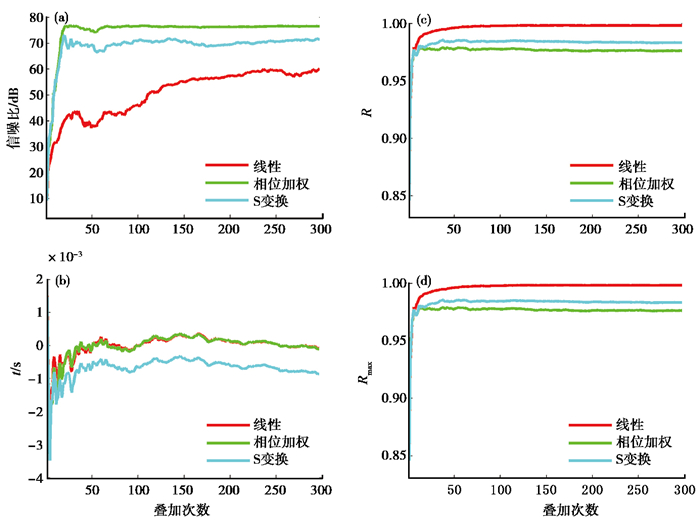
叠加前先进行相同频率滤波,滤波器频率范围设定为2~6Hz。然后用前述的3种叠加方法分别对图 2每条合成记录进行300次叠加,再利用2~6Hz带通巴特沃斯滤波器滤波(王宏禹,1995),最终获得线性叠加结果(图 3(a))、相位加权叠加结果(图 3(b))及S变换叠加结果(图 3(c))。在合成波形记录叠加的过程中,随着叠加次数的增加,进一步计算了每次累积叠加结果的信噪比(熊翥,1993)(图 4(a))、与参考波形之间的时间延迟(罗桂纯等,2008;王彬等,2012)(图 4(b))、直接对齐相关系数(图 4(c))、最大滑动相关系数(Snieder,2006;Stehly et al,2007;罗桂纯等,2008;肖卓等,2015)(图 4(d))等。
|
图 3 300条合成弱信号记录叠加结果 (a)线性叠加;(b)相位加权叠加;(c)S变换叠加 |
|
图 4 合成记录叠加结果的定量评价指标变化曲线 (a)信噪比;(b)叠加结果与模板波形之间的时间延迟;(c)直接对齐相关系数;(d)最大滑动相关系数 |
由图 4(a)可见,相位加权叠加和S变换叠加结果的信噪比较高,明显高于线性叠加,但S变换叠加比相位加权叠加信噪比低;线性叠加记录到第250次左右时信噪比基本饱和,随后信噪比曲线随叠加次数的增加不断振荡,互有抵消,相位加权和S变换叠加结果基本都在第25次叠加处信噪比不再增强,之后信噪比曲线变化平稳,二者仅噪声量级处于不同水平。
由信噪比曲线变化特征可知,基于相位权重的叠加方法,其叠加效率明显高于线性叠加,说明此类叠加可以采用较少记录即可获得与线性叠加更多记录相同的信噪比叠加效果。究其原因,可能是此类方法能够充分挖掘和利用记录序列内部的相位信息,压制尖锐不相干信息,增强相干信息,快速提高叠加信噪比。但是,S变换叠加并没有获得预期的高信噪比效果,这说明时频域信号的任意分割造成相位信息冗余,产生虚假信息,影响和抵冲应有的叠加效果,即信号的频率细分和相位过度加权反而不能获得较高的叠加效率。
2.3 仿真信号叠加质量的可靠性估计强背景噪声下弱信号叠加获得较高的信噪比以增强信号固然重要,而叠加结果的质量则更是应予关注的问题。为此,进一步对叠加波形的质量进行定量估计。将叠加结果与模板波形之间的时间延迟、直接对齐相关系数、最大滑动相关系数等作为波形质量的评价指标。其中,2个相关系数针对波形的相似性,反映的是波形幅度信息;时间延迟则反映波形相位是否发生偏移。利用这2个指标,可定量描述波形形状改变的程度及相位偏移的大小。
由波形时间延迟曲线(图 4(b))、直接对齐相关系数曲线(图 4(c))和最大滑动相关系数曲线(图 4(d))可知,线性叠加结果与模板波形间的直接对齐相关系数最大,接近1.00,波形相似度最高,时间延迟最小,不超过1个采样点,说明波形相位偏移最小;相位加权结果的直接对齐相关系数与线性叠加结果存在一定差距,说明与独立的波形模板的相关性减弱,波形有所畸变,但其优势在于时间延迟与线性叠加结果基本一致,并没有发生明显的相位偏移;S变换叠加结果的直接对齐相关系数较高,介于线性与相位加权叠加结果之间,说明通过更多的时频域信息,一定程度上增加了波形的相似性,但其时间延迟较大,发生了相对明显的相位偏移现象;3种叠加结果的最大滑动相关系数均大于直接对齐相关系数,但三者的分布状态并没有改变。
综上所述,线性叠加虽然对记录信息的利用不够经济,但其结果与模板波形最相似,发生相位偏移最小,最能够保证信号在叠加中没有发生形态变化和质量损失,可以认为其属于“基本无损”的叠加;相位加权与S变换叠加结果只有单项指标较好,说明叠加波形的质量部分符合参考波形的要求,前者叠加波形的优良性能在于较小的相位偏移,不足在于损失了波形的相似性;后者波形相似程度得到一定提升,但存在相对较大的相位偏移,故这2种方法均属“部分有损”的叠加。
3 宾川气枪震源激发信号提取结果的可靠性估计 3.1 宾川气枪主动源简介2011年中国地震局地球物理研究所和云南省地震局在滇西地震预报实验场核心区域、活动强烈的红河断裂北段与程海断裂之间建立了宾川主动源发射台,在其周围布设了40套短周期地震仪组成的密集观测台阵,形成了完整的人工主动震源发射观测系统,旨在利用人工震源主动向地下发射地震波,进行地壳介质监测,变被动监测为主动探察;并通过连续激发实现动态跟踪地震波走时变化,进一步分析地震波速参量的时间演化特征,最终为该地区地震活动后续发展趋势的判定提供科学判据(陈颙等,2005;徐荟,2013;王彬等,2015;刘自凤等,2015)。
3.2 气枪震源弱信号提取结果的信噪比估计与波形质量可靠性分析 3.2.1 气枪震源激发重复弱信号的叠加提取与评价指标的计算随机选择宾川主动源发射台53267台站的记录作为评价气枪震源激发弱信号叠加提取效果及可靠性的实例,实施以下操作:
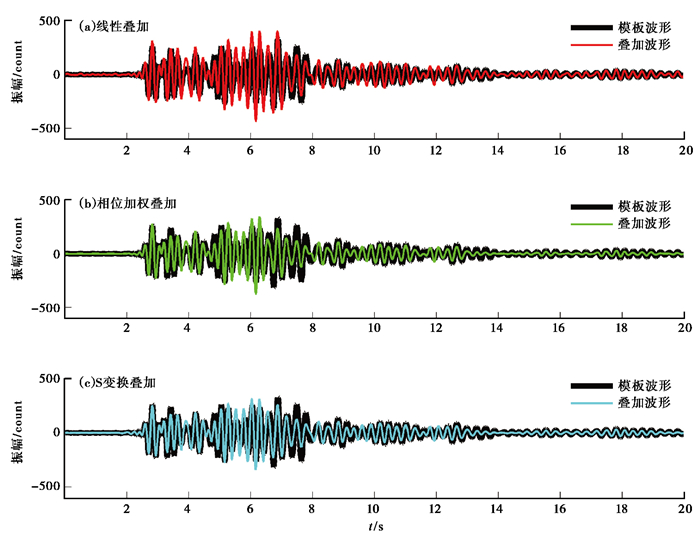
(1) 形成模板波形。为了使3种方法的叠加效果具有一定的可比性,从53267台2000次原始观测记录中随机选取1000枪(杨华中等,1996),直接采用线性方法对其叠加,其结果作为线性、相位加权和S变换等3种叠加方法提取气枪震源弱信号实际效果综合评价的模板波形,亦可称为参考波形(图 5)。
|
图 5 53267台站300条气枪垂直向记录叠加结果 |
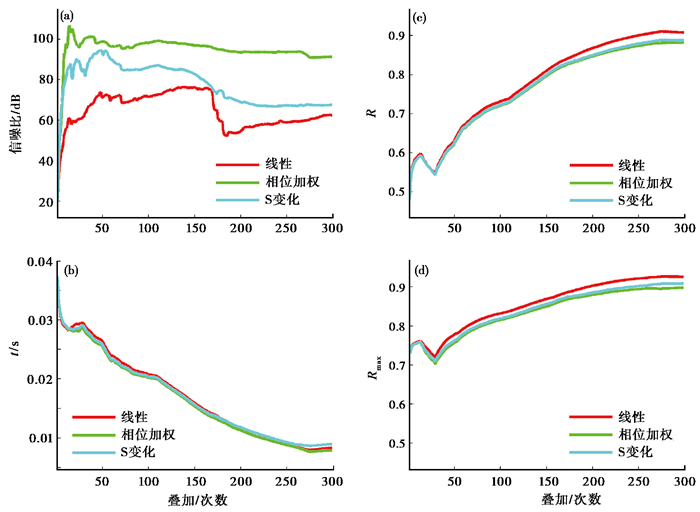
(2) 计算评价指标。从上述1000条记录中再随机抽取300枪(杨华中等,1996),分别采用3种方法叠加每条包含有随机噪声的弱信号(图 1),获得相应方法的叠加结果(图 5)。在每条记录逐次叠加过程中,分别计算了累积叠加结果的信噪比(图 6(a))、与模板波形间的时间延迟(图 6(b))、直接对齐相关系数(图 6(c))及最大滑动相关系数(图 6(d)),用于进一步定量估计3种方法叠加实际记录的效率和波形质量。
|
图 6 气枪震源信号叠加结果的定量评价指标变化曲线 (a)信噪比;(b)叠加结果与模板波形之间的时间延迟;(c)直接对齐相关系数;(d)最大滑动相关系数 |
由图 6(a)53267台站计算结果可见,相位加权叠加结果的信噪比最大,线性叠加结果的最小,而S变换叠加结果介于二者之间;相位加权叠加信噪比大约在第15次叠加时就达到最大,然后稍有下降,之后基本没有较大的起伏变化,S变换叠加结果的信噪比也是如此,二者变化形态基本类似,只是S变换随着叠加次数的增加,信噪比反而还有所加速下降,线性叠加结果的信噪比总体趋势是随叠加次数的增加而不断增大,但在第15、50、175次叠加左右存在局部信噪比下降的现象,形成叠加信噪比不同程度的振荡。
同理,在对参与叠加的原始记录不进行任何挑选和处理的情况下,进一步对其它台站也进行了类似计算。虽然叠加结果的信噪比变化特征有一定差别,但大部分台站存在类似的波动现象,只有少数台站信噪比随叠加次数的增加而一直增大,但达到一定叠加次数后,信噪比则缓慢增加,或存在饱和现象。
以上3种叠加的信噪比变化特征说明,原始波形记录质量参差不一,包含的噪声成分复杂,导致一些原始记录参与叠加时“消极怠工”,使叠加信噪比随叠加次数的增加出现振荡或缓慢增长趋势。所以,在将波形记录叠加前都要经过认真筛选和质量控制。
3.2.3 信号叠加质量的可靠性估计由图 6(c)可知,线性逐次叠加结果与模板波形之间的直接对齐相关系数最大,波形振幅最逼近;S变换、相位加权叠加结果波形相似性依次减弱,但与线性叠加结果基本相近,说明3种叠加结果与模板波形之间的形状都极其相似。而从图 6(b)时间延迟曲线来看,三者叠加结果的时间延迟也都很小,不超过3个采样点,S变换相对而言稍大,但也在允许的误差范围内,真实信号并没有发生较大的相位偏移,基本保持了波形信号原有的质量状态和分布性质。图 6(d)通过叠加结果与参考波形间滑动,使波形间相关系数达到最大,结果发现最大滑动相关系数均有一定的增大,但以上3种方法叠加结果的基本分布状态并没有因为波形滑动而发生质量分布状态的改变。由图 6(a)~6(d)综合对比可知,随着叠加次数的不断增加,信噪比不一定都增加,而是或有所下降,或持续振荡,但定量描述波形质量的3种指标始终向好发展。
对波形质量评价指标的综合效果而论,在次数足够多的叠加条件下,线性方法最大可能地保持了波形的信号质量,没有改变原始信号的分布状态及形态;而相位加权和S变换叠加也基本上没有较大改变波形的相位信息和波形形状,其叠加质量与线性叠加结果基本相近,只是相位加权叠加的波形相似性稍差,而S变换叠加结果与模板波形间存在稍大的相位偏移。
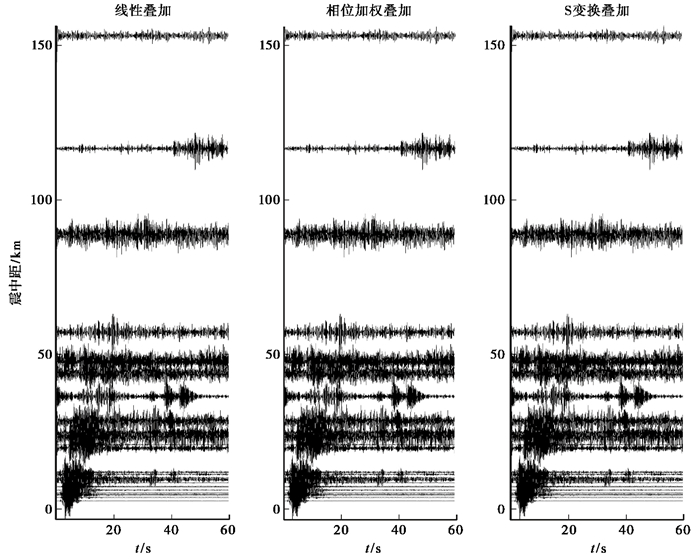
3.3 利用3种叠加方法提取台站时-距曲线通过上述数值仿真和气枪震源激发资料的实际处理可以发现,3种方法的处理性能及可靠性各有优劣,但都能不同程度地有效提取强噪声背景下的弱信号,只是在相同的叠加次数条件下,相位加权和S变换叠加效率更高。基于此,下面利用3种叠加方法实际提取宾川主动源相关台站的时-距曲线,以考察其叠加效率和波形质量。叠加原则如下:叠加1次和50次;2~6Hz带通滤波;通过采样点抽取,形成50Hz采样率;记录持续60s,包含所有气枪震源激发信号;选择固定台站记录,最远台站震中距151km。通过逐台叠加1次和50次,分别得到如图 7、8所示的台站时-距曲线。
|
图 7 1枪不同震中距台站波形记录叠加的时-距曲线 |
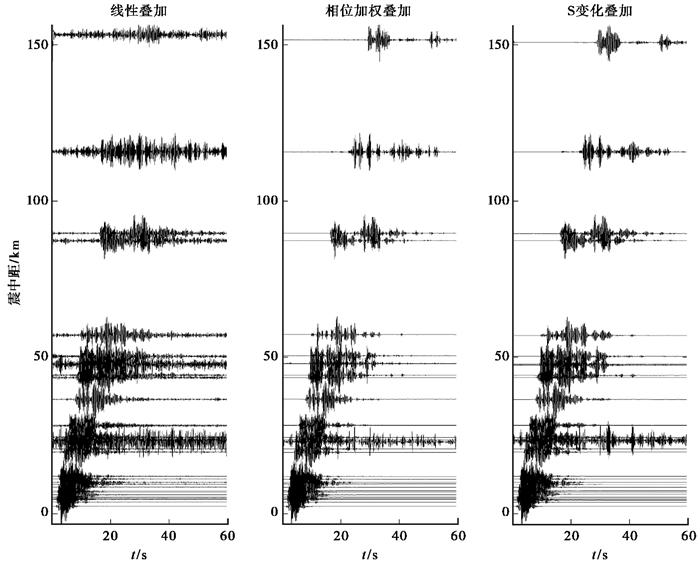
|
图 8 50枪不同震中距台站波形记录叠加的时-距曲线 |
由图 7、8可见,1枪叠加时,近场波形记录信号比较清晰,远场信号比较弱,随着震中距的不断增加,震源激发的弱信号逐渐淹没在强噪声背景之下。但当叠加50枪记录时,远、近场叠加波形均基本清晰。这说明通过不同方法的叠加,一方面能够降低强背景噪声的水平,另一方面可将弱信号明显增强。从50枪叠加结果也可看出,S变换叠加波形更加清晰,相位加权叠加波形清晰但波形质量感觉稍差,线性叠加波形相对而言比较模糊,说明当前线性叠加结果还不足以使远场弱信号显著增强。
综合分析50枪的最终叠加波形效果后发现,S变换和加权叠加方法均能达到有限记录、高效叠加、基本保真的叠加目标。初步认为,其清晰的波形结果已可用于震相识别、初动拾取、走时分析、结构研究等相关地震学研究工作中,而线性叠加还需更多的记录,才可能清晰提取相关波形的研究数据。
4 讨论与结论 4.1 讨论(1) 气枪震源激发的弱信号叠加后的信噪比估计和波形质量可靠性分析并没有考虑其它因素。若改变叠加条件,如叠加前不滤波,结果会存在细微差异,但也未改变叠加后的信噪比和波形质量的排序。究其原因在于,线性叠加与相位加权叠加在高噪声时易受噪声分布的影响,抗噪能力弱;而S变换叠加(Schimmel et al,2011)基于时频域数据(Stoekwell el al,1996),相当于带通滤波,单一信号,抗噪能力增强,结果反而稍好。因此,线性和相位加权叠加前最好滤波,以提高波形叠加的信噪比。
2) 合成数据的性质简单,随机分布均匀,随着叠加次数的增加信噪比不断提高;而实际气枪震源激发时台站接收的信号成份复杂,会受各种干扰因素的影响,距理想的随机均匀分布状态还存在较大差距,因此随叠加次数的增加,信噪比存在饱和、下降趋势或振荡变化等现象,但波形叠加质量始终存在向好趋势。所以,选择叠加次数时需要考虑的因素很多,若单纯从叠加效益考虑,应依赖叠加信噪比×叠加质量达到最大时的叠加拐点,这需要处理实际数据时科学把握,以便获得更为合理的波形叠加质量和记录叠加效率。
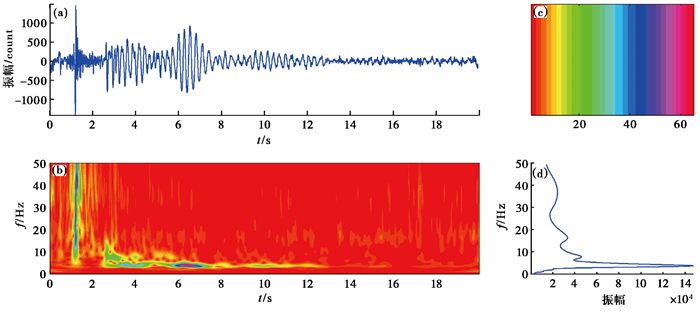
(3) 对于气枪震源激发的信号,不同研究者采用的滤波范围存在差异,本文根据记录的时频(Stoekwell el al,1996)和边际谱能量分布特征(图 9),并参考其它研究者的相关结果(刘自凤等,2015;徐荟,2013),确定气枪震源弱信号滤波范围2~6Hz比较合理。因此,在前述的计算中均采用5阶巴特沃斯带通滤波器进行2~6Hz信号滤波,这样明显降低了强背景随机噪声和不规则干扰的影响(图 1),突出了气枪震源弱信号增强的效果,使通过叠加提取气枪震源弱信号所处的频率范围更具有针对性,最终提高叠加结果的信噪比、稳定性与可靠性。
|
图 9 气枪震源信号的时频分布及其边谱曲线 (a)单条气枪记录;(b)时频分布图;(c)时频分布图对应的颜色图标;(d)时频分布图对应的边谱图 |
(4) 虽然S变换叠加结果与模板波形间的相似度比相位加权叠加结果高,但其叠加信噪比却比后者低,相位偏移现象也相对严重。究其原因,可能是这2种方法虽然都利用相位信息消除随机尖锐噪声,突出相干信号,挖掘更多的数据内部信息,但信号频率的任意分割,一方面造成噪声相位值在时频域分布不够集中,每个频带内因信息量匮乏反而得不到充分叠加,使得时频域叠加信噪比下降;另一方面也造成时频域信息大量冗余,在叠加过程中不断形成相位累积误差,使叠加结果的相位偏移现象更为严重。
(5) 气枪震源激发的弱信号并非完全已知,但基于信号的重复性和噪声的随机性,通过对记录的充分直接叠加不断逼近震源弱信号,其结果在一定程度上能够代表震源激发的弱信号,将其作为比对的模板波形自然可行;而在具体测试3种方法叠加结果的实际性能时,随着叠加次数的增加,叠加信号的随机噪声不断减弱,有效信号越来越逼近模板波形,这也意味着越来越逼近震源激发的真实微弱信号。因此,3种方法的逐次叠加结果与模板波形、震源弱信号的相关性越来越强,与噪声则越来越不相干,这也是在解决同类问题时常采用叠加技术提取弱信号的理论依据。
4.2 结论(1) 无论是合成数据仿真,还是气枪信号实际叠加处理,均表现出3种方法叠加结果的信噪比随叠加次数的增加而增大,演化趋势基本一致,基于相位加权的2种叠加结果信噪比均比线性叠加高,其中相位加权叠加信噪比又比S变换叠加更高。这说明基于相位的2种叠加方法,无论在时间域还是在时频域内,均充分利用和最大限度挖掘了波形内部相位的相干信息,与线性叠加相比,能够以较少记录获得高信噪比叠加效果,属于“经济型”叠加方法。
(2) 由波形相关与时间延迟指标综合评价波形叠加的质量和可靠性不难发现,线性叠加没有造成明显的原始信号幅度的损失和相位偏移,基本实现了波形保真叠加效果,而相位加权和S变换叠加虽然能够充分利用相位信息,但在获得叠加信噪比优势的同时,也部分损失了波形的叠加质量。即相位加权叠加结果虽然没有较大的相位偏移,但波形相似度差别较大,产生了波形畸变;而S变换叠加虽然保持波形相似度较高,却存在相位偏移量较大的现象。
(3) 综合考虑信号叠加的效率和质量,在利用气枪震源重复激发的弱信号解决地震科学问题时,应根据研究目标和实际资料状况形成强背景噪声下弱信号提取的技术方案,即如果气枪震源重复激发次数充分,且相关工作要求波形质量较高时,建议采用线性叠加进行弱信号提取;若气枪震源激发次数有限,且要求时间精度较高时,相位加权叠加方法应是首选;若要求波形质量较高时,S变换叠加方法应是首选。
因此,通过叠加方法的合理选择有效进行强背景噪声下弱信号的科学提取,能够为气枪主动源地震学的深入研究提供初动、震相、波形等相对可靠的基础研究资料。
致谢: 本研究利用了云南宾川地震信号发射台的气枪震源激发的记录资料,得到了云南省地震局王彬研究员的大力支持和帮助,匿名审者及周元泽博士也提出了宝贵的修改意见,在此一并表示衷心的感谢。| 陈颙, 李宜晋. 2007, 地震波雷达研究展望:用人工震源探测大陆地壳结构. 中国科学技术大学学报, 37(8): 813–819. |
| 陈颙, 朱日祥. 2005, 设立"地下明灯研究计划"的建议. 地球科学进展, 20(5): 485–489. |
| 刘自凤, 苏有锦, 王宝善, 等. 2015, 宾川主动源地震波走时变化分析方法研究. 地震研究, 38(4): 591–597. |
| 罗桂纯, 葛洪魁, 王宝善, 等. 2008, 利用相关检测进行地震波速变化精确测量研究进展. 地球物理学进展, 23(1): 56–62. |
| 牟永光. 1986, 地震勘探资料数字处理方法. 北京: 石油工业出版社. |
| 王彬, 吴国华, 苏有锦, 等. 2015, 宾川地震信号发射台的选址, 建设及初步观测结果. 地震研究, 38(1): 1–6. |
| 王彬, 杨润海, 王宝善, 等. 2012, 地震波走时变化精确测量的实验研究. 云南大学学报(自然科学版), 34(增刊Ⅱ): 15–20. |
| 王宏禹. 1995, 数字信号处理专论. 北京: 国防工业出版社. |
| 肖卓, 高原. 2015, 尾波干涉原理及其应用研究进展综述. 地震学报, 37(3): 515–526. |
| 熊翥. 1993, 地震数据数字处理应用技术. 北京: 石油工业出版社. |
| 徐荟, 2013, 利用主动震源初至波研究小江断裂带浅层波速变化, 硕士学位论文, 23~38, 北京: 中国地震局地球物理研究所. |
| 杨华中, 汪蕙. 1996, 数值计算方法与C语言工程函数库. 北京: 科学出版社. |
| 苑益军, 周芝旭, 牛滨华. 2005, 浅谈地震资料处理中的提高信噪比处理技术. 石油地球物理勘探, 40(2): 168–171. |
| Schimmel M, Paulssen H. 1997, Noise reduction and detection of weak, coherent signals through phase-weighted stacks. Geophy J Int, 130: 497–505. DOI:10.1111/gji.1997.130.issue-2. |
| Schimmel M. 1999, Phase cross-corelations:design, comparisons and applications. Bul1 Seism Soc Am, 89: 1366–1378. |
| Schimmel M, Stutzmann E, Gallart1 J. 2011, Using instantaneous phase coherence for signal extraction from ambient noise data at a local to a global scale. Geophys J Int, 184: 494–506. DOI:10.1111/gji.2010.184.issue-1. |
| Snieder R. 2006, The theory of coda wave interferometry. Pure Appl Geophys, 163: 455–473. DOI:10.1007/s00024-005-0026-6. |
| Stehly L, Campillon M, Shapiro N M. 2007, Travel time measurements from noise correlation:stability and detection of instrumental time-shifts. Geophys J Int, 171(1): 223–230. DOI:10.1111/gji.2007.171.issue-1. |
| Stoekwell R G, Mansinha L, Lowe R P. 1996, Localization of the complex spectrum:the S-transform. IEEE transactions on signal processing, 17(6): 998–1001. |
 2016, Vol. 32
2016, Vol. 32


