2. 蒙城地球物理国家野外科学观测研究站, 安徽亳州 233527;
3. 安徽省勘查技术院, 合肥 230031;
4. 中国地质科学院地质力学所, 北京 100081
2. Mengcheng National Geophysical Observatory, Bozhou 233527, Anhui, China;
3. Geological Exploration Technologies Institute of Anhui Province, Hefei 230031, China;
4. Institute of Geoemechanics, Chinese Academy of Geological Sciences, Beijing 100081, China
相对于天然地震或传统的爆炸源,基于气枪源的主动源探测有其特有的优点,是了解地下结构及其变化的重要手段(陈颙等,2007;林建民等,2008;唐杰等,2009;杨微等,2009)。与天然地震相比,气枪主动源激发的重复性高,根据需要可以在同一个地点重复激发,因此有利于研究地下介质的变化。与传统的炸药爆破源相比,气枪震源与水耦合性好,转换效率高,因此,产生同样震级的人工地震比爆炸源更经济。另外,气枪源激发的优势频率为低频,传播时不容易衰减,在介质中可传播得更远、更深。
为了提高气枪源激发信号的信噪比,通常在1个点进行重复激发,然后对得到的信号进行叠加。传统的叠加方法是线性叠加方法,该方法对气枪源在不同时间激发的信号采用相加的方法直接进行叠加。线性叠加方法不会使有效信号的相位失真,但叠加得到的信号的信噪比较低。Rawlinson等(2004)提出的自适应叠加方法相当于对波形数据进行了线性叠加。对于信噪比低的数据,线性叠加不能很好地压制噪声。相比而言,在波形叠加中将相位信息作为权重因子引入的相位加权叠加,能较好地压制噪声,提高信噪比(Schimmel et al,1997、2011;江国明等,2012)。但是,在噪声较强的情况下,相位加权叠加会不可避免地在有效气枪信号到达之前出现一些人为信号,导致初至拾取困难,误差较大,影响了气枪用于地下介质速度成像的效果。
为了解决上述问题,我们利用叠加气枪信号在相距较近台站具有相似性的特点,通过互相关方法提取较精确的到时差。然后,利用台站对双差地震成像算法(Zhang et al,2010、2016) 进行P波三维速度成像。本文首先介绍长江安徽段气枪主动源实验庐江台阵布设情况,然后对比绝对到时拾取和基于波形互相关的台站对走时差数据,最后利用台站对走时差数据确定地下速度结构。
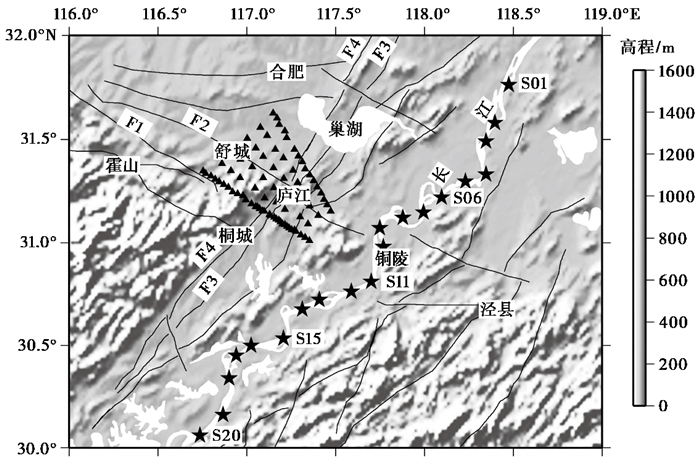
1 长江安徽段气枪主动源实验庐江地震台阵2015年10月沿长江安徽段进行的气枪主动源实验中,气枪船在20个固定点进行了重复激发(图 1)。以铜陵气枪源固定激发点为中心,中国科学技术大学联合中国地质力学研究所在郯庐断裂带庐江段布置了1个扇形台阵(图 1)。该临时观测台阵包括90个地震仪,其中,50个REFTEK130+L22E型短周期地震仪,40个CMG-40T-1型短周期地震仪,所有地震仪的采样率均设定为200Hz。根据临时观测台阵覆盖和密集布设的要求,为了尽可能提高气枪源地震数据质量,在选址时尽量避开了居民区、公路旁等噪声较大的区域,并尽可能深挖坑,将地震仪放置在基岩或坚硬地层上。
|
图 1 长江安徽段气枪主动源实验庐江临时地震台阵分布 三角形为临时观测台站;20个黑色五角星为沿长江的20个固定气枪激发点;黑线为断层;F1金寨-西汤池断裂;F2独山-东汤池断裂;F3郯庐断裂;F4池太断裂 |
庐江临时地震台阵包括:① 2条线性台阵:西南端1条加密线性台阵,跨过郯庐断裂带和大别山东缘,长约70km,平均台间距约3km,断裂带附近加密到约1.5km,指向铜陵气枪源,共33个台站;东北端线性台阵平均台间距约4km,长约68km,共17个台;② 1个小孔径台阵:以西南线性台阵中心台站为中心,布设1个小孔径台阵,直径2km,共10个台站;③ 在2条线性台站中间,平均台间距8km布设面状观测系统,共30个台站。对于20个固定点的气枪激发,庐江地震台阵有74~76个台站接收到了有效的气枪信号(表 1)。
| 表 1 20个固定点的气枪重复激发次数和接收到有效信号的庐江台阵台站数 |
庐江台阵所处区域出露的地层位于秦岭-大别地层区北淮阳地层分区和扬子地层区的下扬子地层分区,岩性主要为北淮阳岩浆岩带的下扬子岩浆岩带,所处的大地构造位置主要为北淮阳构造带、下扬子前陆盆地和沿江隆凹褶断带。研究区内断裂非常发育,郯庐大断裂(F3) 南端经过研究区,走向为NE向,独山-东汤池断裂(F2) 经过舒城的汤池镇和庐江县城,池太深断裂(F4) 经过柯坦镇与桐城市(图 1)。
2 庐江地震台阵气枪源数据叠加气枪源数据的高度可重复性使我们能在1个点重复多次激发,因此,由1个气枪源即可得到很多重复的人工地震数据(表 1)。对于庐江临时地震台阵接收到的重复气枪信号,由于知道精确的发震时刻,因此,我们分别采用线性叠加和时间频率域相位加权叠加的方法得到叠加信号。气枪信号的优势频率为2~8Hz(林建民等,2008),为了提高气枪信号叠加效率,对原始资料减采样到25Hz。时间频率域相位加权叠加由相位加权叠加拓展得到(Schimmel et al,1997),如下所示
| $ g(t) = \frac{1}{N}\sum\limits_{j = 1}^N {{S_j}\left(t \right)} {\left| {\frac{1}{N}\sum\limits_{k = 1}^N {\exp \left[ {i{{\mathit{\Phi}} _k}\left(t \right)} \right]} } \right|^v} $ | (1) |
其中,N为气枪重复激发次数;Φk(t)为第k次激发所接收到气枪记录的瞬时相位信息;Sj(t)为同一台站第j次激发所接收到的气枪记录;ν为控制相位加权叠加的指数,当ν=0时即为线性叠加。每个线性叠加的采样点都被瞬时相位的相干性进行加权,较弱的、但相干性好的信号会被加强,而相干性不好的噪声将被压制。对式(1) 经过1个S变换就可得到时间频率域的相位加权叠加(Schimmel et al,2011)。
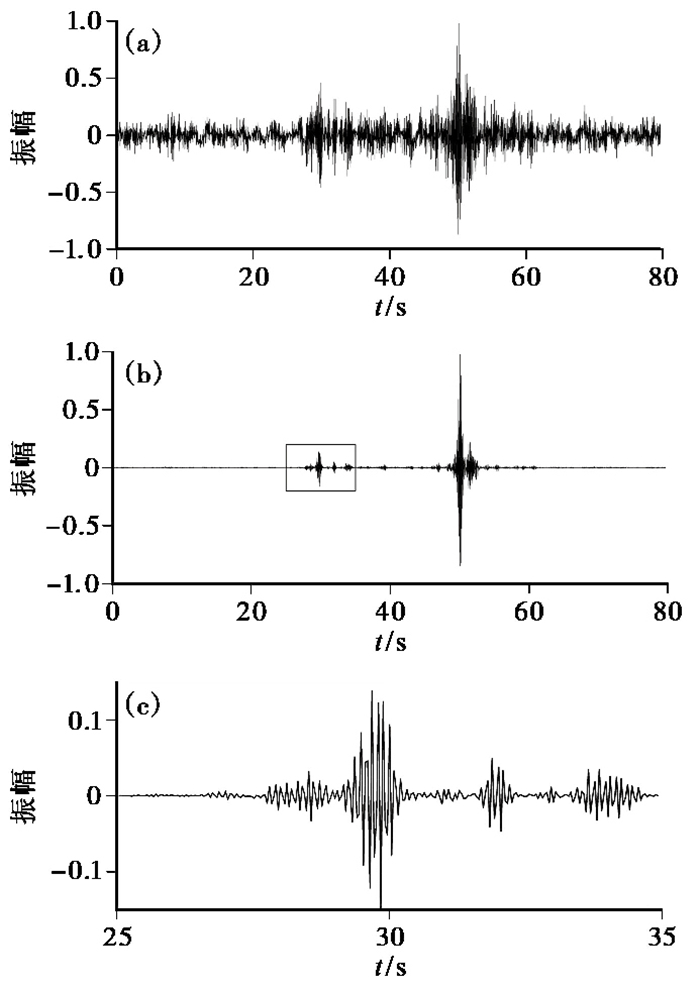
我们选取了在S01固定点激发的气枪源在A05台站接收的Z分量数据对2种叠加方法进行比较,震中距约为163.3km(图 2)。由图 2可见,相位加权叠加的方法更好地压制了噪声,与利用线性叠加得到的波形数据相比,能更好地识别出震相。
|
图 2 A05台站接收到的在S01固定点重复激发的气枪源Z分量叠加数据 (a)线性叠加;(b)相位加权叠加;(c)为(b)中矩形框范围内放大的波形图(a)、(b)中30s左右为P波波形数据;50s左右为S波波形数据 |
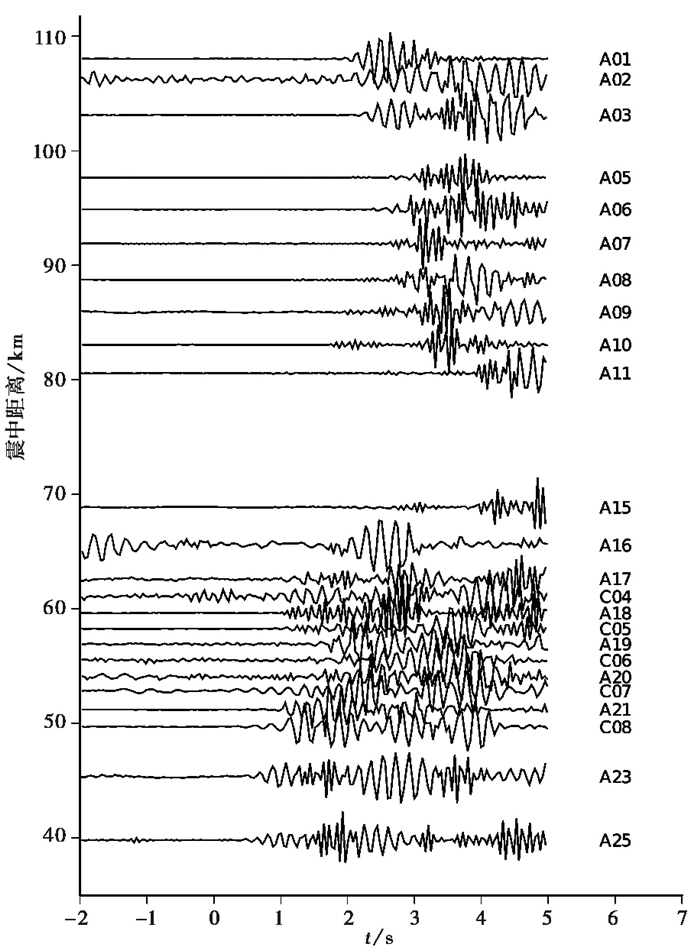
利用时间频率域相位加权叠加得到的数据进行初至拾取时存在较大困难。图 3为S11气枪源沿西南端测线的相位加权波形,由图 3可见,P波信号到达的时间不易确定,进行人工拾取时主观性较强。为了辅助人工到时拾取,我们利用crust1.0速度模型计算了理论到时,并标注在地震波形记录上。由于该地区的结构比较复杂,可以预料基于crust1.0速度模型计算的理论到时与实际到时之间存在偏差。但是,该理论到时仅用于实际到时拾取的参考,不会影响最终的到时拾取结果。
|
图 3 S11气枪源沿西南端测线的相位加权波形 横轴为速度6km/s的折合走时 |
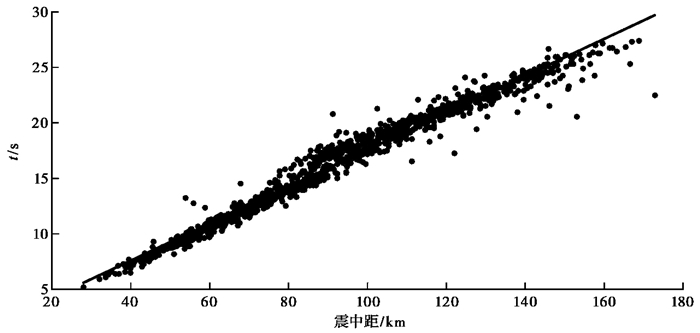
随着震中距的增大,Pg波之前会逐渐出现Pn波,但Pn波振幅相对较低,导致初至拾取困难。我们一共拾取了1112个Pg波到时,其中386个质量不好的数据被剔除。图 4为拾取的Pg波的时-距曲线,由图 4可见,拾取的Pg波走时整体分布在斜率为1/6的直线附近,表明拾取的Pg波的走时数据质量尚可,该地区地壳的平均速度约为6km/s。但是,时-距曲线的斜率在震中距90km左右存在明显变化,即前、后时-距曲线的斜率不同,这意味着在地壳中存在一个高速异常。另一组独立拾取的时-距曲线也存在同样的特征,表明时-距曲线斜率的变化是真实的,即在研究区域下方存在一个高速异常。事实上,庐江台阵所在区域所包含的庐枞火山岩盆地中分布着燕山期中性侵入岩体(安徽省地质矿产局,1982),对应着高速异常,进而导致人工拾取的Pg震相在90km左右其时-距曲线的斜率不同。
|
图 4 人工拾取的Pg波时-距曲线 黑线的斜率为1/6 |
为了得到更精确的到时数据,克服人工拾取带来的误差,我们对同一气枪震源到不同台站的相位加权叠加后的波形数据进行互相关分析,得到同一震相在不同台站的走时差,如下式
| $ C\left(t \right) = \smallint _{_{ - \infty }}^{^\infty }f\left(\tau \right)g\left({t + \tau } \right){\rm{d}}\tau {(\smallint _{_{ - \infty }}^{^\infty }{f^2}\left(\tau \right){\rm{d}}\tau \smallint _{_{ - \infty }}^{^\infty }{g^2}\left(\tau \right){\rm{d}}\tau)^{1/2}} $ | (2) |
其中,f(t)、g(t)为2列波的波形信息;C(t)为2列波的互相关系数;对应最大互相关系数的时刻t为2列波形的到时差。
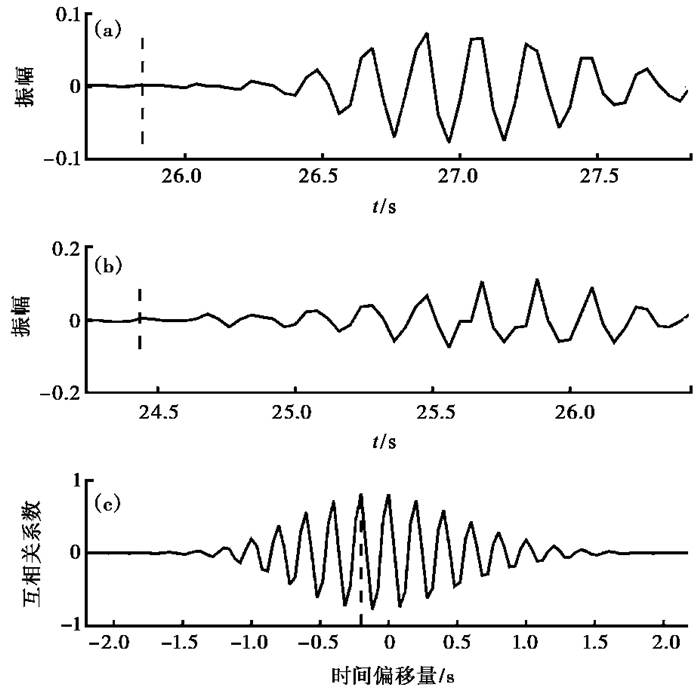
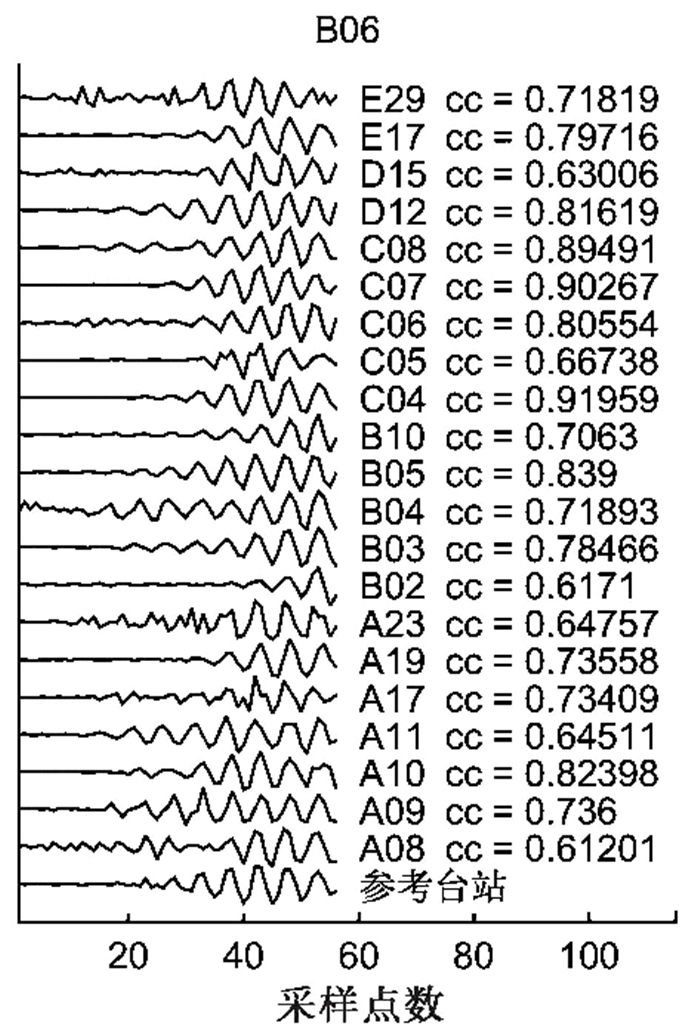
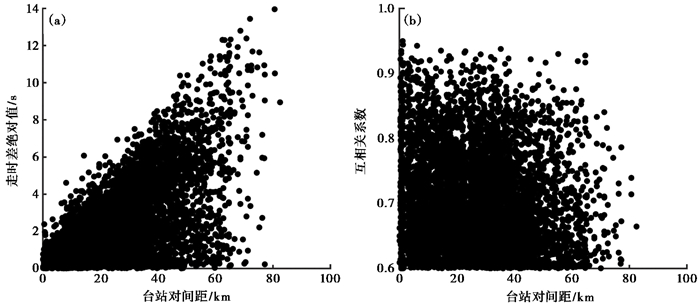
进行波形互相关分析之前,首先需要确定波形分析的时间窗口,我们以拾取的Pg波到时为依据,向前、后分别取0.2s确定为时间窗口,然后进行互相关计算。图 5为对2个台站接收到的同一气枪源的波形进行互相关分析的过程。由图 5可见,Pg到时的拾取存在较大的不确定性,对于不同的数据分析员,拾取的到时可能存在较大差别。但是,波形互相关计算得出的是时间窗口内主要波形的相对走时差,而几乎不受主要波形前较小振幅波形的影响,因此波形互相关得出的台站之间的走时差更为准确。我们注意到,波形互相关可能会出现周波跳跃现象,但对于气枪主动源信号,因为频率较低,高频成分较少,因此出现周波跳跃的可能性相对较小。另外,波形互相关所选取的时间窗口是基于人工拾取到时确定的,可以保证在较短的时间窗内包含了有效的信号,这在某种程度上也降低了周波跳跃发生的概率。图 6显示了对于同一个气枪源的相位加权叠加数据,即以某个台站为参考,其它台站上的波形数据利用波形互相关进行对齐之后的结果。由图 6可见, 波形的主要相位对应整齐,相关系数为0.6~0.92。通过台站对波形互相关计算,我们最终得到了6073个互相关系数大于0.6的走时差数据(图 7)。由图 7可见,虽然整体来说随着台站间距的减小,波形的相似性也更高,但是台站间波形的相似性与台站间距的关系比较复杂。另外,走时差随台站间距的增加一般呈增加趋势,但是二者之间并不是一个简单的线性关系。这表明在该区域存在较强的速度变化。
|
图 5 2个台站接收到的同一气枪主动源波形的互相关分析 (a)台站A11(震中距153.683km)接收到的波形信号,虚线指向P波到时;(b)台站A17(震中距144.2947km)接收到的波形信号,虚线指向拾取的P波到时;(c)2个台站接收到的波形的互相关分析(台间距20.177km,互相关系数为0.818,走时差为1.211s),虚线指向最大互相关系数 |
|
图 6 基于参考台站纪录到的波形、利用互相关分析对其它台站记录的波形进行波形对齐的结果 每个台站后面为波形互相关系数 |
|
图 7 台站对波形互相关统计结果 (a)所有台站对的走时差与台站对间距的关系;(b)台站对互相关系数与台站对间距的关系 |
基于事件对的双差地震速度成像方法(Zhang et al,2003、2006),是利用事件对在同一台站的到时差数据,实现地震位置以及速度结构的联合反演。由于从相邻地震发出的2条射线在源区外近乎重合,因此,相应的源区外的速度变化对到时差的影响非常小,可以消除源区外速度结构误差的影响。此外,更准确的到时差数据可以直接通过波形互相关技术得到,因此地震位置以及源区内速度结构的准确性有很大提高。目前,该方法已被广泛用于中、小尺度区域的速度结构研究中(Zhang et al,2006)。
同理,基于台站对的双差地震速度成像方法(Zhang et al,2010、2016),是利用一对台站对同一事件记录到的走时差数据,联合反演地震位置以及速度结构。事件i到台站j、k的观测到时和预测到时的残差可用地震震中、发震时刻、速度结构以及台站校正项的扰动量等线性表示如下
| $ r_{_j}^{^i} = \sum\limits_{m = 1}^3 {\frac{{\partial T_{_j}^{^i}}}{{\partial x_{_m}^{^i}}}} \Delta x_{_m}^{^i} + \smallint _{_i}^{^j}{\rm{\delta }}u{\rm{d}}l + \Delta {\tau ^i} + {s_j} $ | (3) |
| $ r_{_k}^{^i} = \sum\limits_{m = 1}^3 {\frac{{\partial T_k^{^i}}}{{\partial x_{_m}^{^i}}}} \Delta x_{_m}^{^i} + \smallint _{_i}^{^k}{\rm{\delta }}u{\rm{d}}l + \Delta {\tau ^i} + {s_k} $ | (4) |
式中,rji、rki为事件i到台站j、k的到时残差;T为地震走时;x、dx为震中坐标及其扰动量;τ为发震时刻;δu为慢度的扰动量;dl为离散的射线路径的一个单元;sj、sk分别为台站j、k的台站校正量。式(4) 减去式(3),可以得到
| $ r_{_j}^{^i} - r_{_k}^{^i} = \sum\limits_{m = 1}^3 {\left({\frac{{\partial T_{_j}^{^i}}}{{\partial x_{_m}^{^i}}} - \frac{{\partial T_k^{^i}}}{{\partial x_{_m}^{^i}}}} \right)} \Delta x_{_m}^{^i} + \int\limits_i^j {\rm{\delta }} u{\rm{d}}l - \int\limits_i^k {\rm{\delta }} u{\rm{d}}l + {s_j} - {s_k} $ | (5) |
此外,因为2条射线在源区内会有一定程度的重合,因此,相应源区内的速度变量的偏导数就会趋近于0,一定程度上可以消除源区内速度结构误差的影响,提高地震定位以及源区外速度结构反演的准确性。该方法已被应用于非火山型震颤信号的定位(Zhang et al,2010)以及地震颤动区域的速度成像(Zhang et al,2016)。
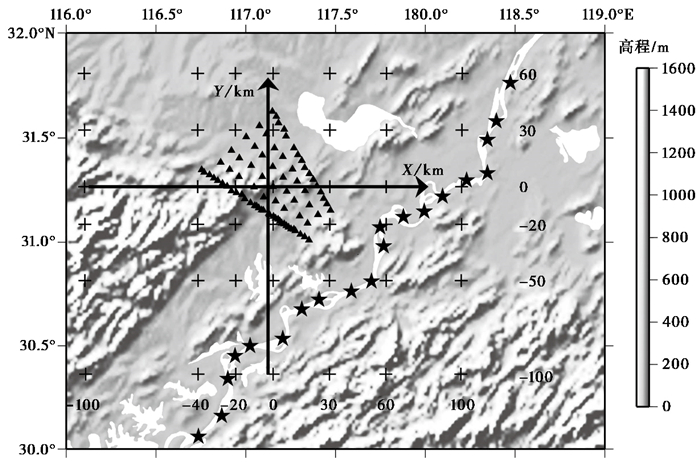
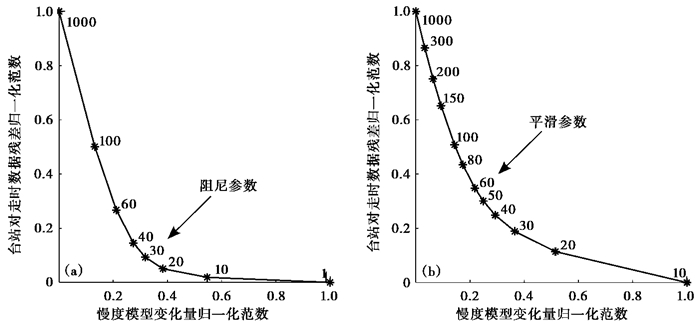
在长江气枪源实验中,我们希望得到的是密集台阵区域下方的速度结构,故此时可用台站对的双差层析成像方法。由于受气枪源和台站分布的限制,我们无法得到1个很精细的三维速度结构。所以,我们的反演网格设置比较稀疏,分别为X:-100、-40、-20、0、30、60、100km;Y:-100、-50、-20、0、30、60km;Z:0、2、5、10、15、20、25、30km。坐标系原点位于31.26584°N、117.15253°E(图 8)。对于台站对双差地震层析成像系统,我们通过对慢度模型改变量进行平滑、阻尼约束而使得反演系统稳定(Zhang et al,2003)。为了选取合适的平滑、阻尼参数用于反演系统,通过改变平滑、阻尼参数,构建反映慢度模型改变量和走时残差平衡关系的L型曲线,然后选取曲线拐点区域所对应的参数为合适的反演参数(Aster et al,2013)。通过L型曲线分析可见,阻尼参数20~40位于拐点区域,所以选择阻尼参数30用于反演(图 9)。对于平滑参数的选择,L型曲线显示出平滑参数20~60为拐点区域,基于模型异常的稳定性考虑,最终选择平滑参数为60(图 9)。初始速度模型由利用全国的面波数据反演得到的该区域三维横波速度模型,然后通过纵波、横波速度的经验关系得到(Shen et al,2016),该模型比crust1.0速度模型更准确。
|
图 8 速度反演网格点(十字架)分布 X轴、Y轴分别指向正东、正北方向;坐标原点为交叉点;三角形为临时观测台站;五角星为20个固定气枪激发点 |
|
图 9 慢度模型变化量归一化范数和台站对走时数据残差归一化范数之间的L曲线 (a)平滑参数固定为60时改变阻尼参数得到的L曲线;(b)阻尼参数固定为30时改变平滑参数得到的L曲线 箭头所指为选取的阻尼参数和平滑参数 |
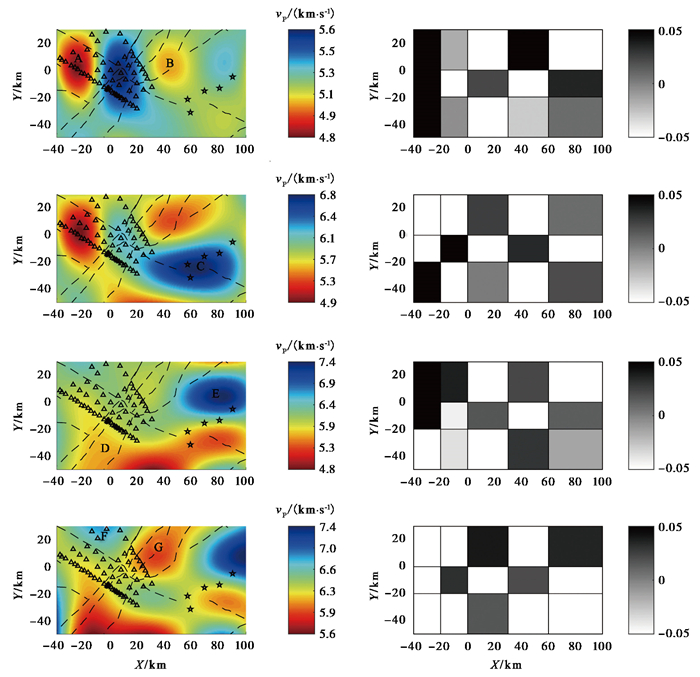
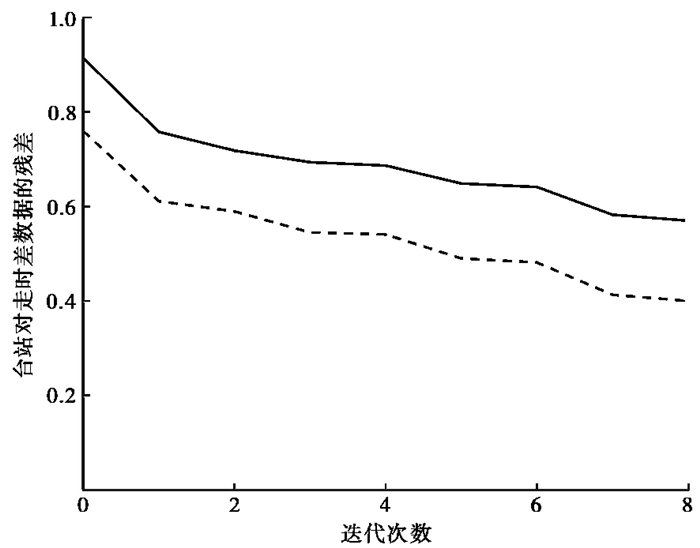
首先,使用传统的棋盘分辨率测试方法检验当前网格设置下的速度模型反演的可靠性。我们设置棋盘模型为初始模型的相邻网格的速度值加上±5%的扰动值,并用该棋盘模型合成走时,进而根据实际的台站对走时差数据来构建合成数据。然后,使用该合成数据以及初始模型进行反演,测试棋盘模型的恢复情况。图 10显示在当前的数据和网格点分布情况下,在深度2~15km的范围内棋盘模型能够较好地恢复,表明利用台站对双差走时成像算法可以获得庐江地区较好分辨率的速度模型。图 11显示了台站对走时差数据随迭代次数的均方根残差和加权均方根残差的变化。此处,权重是根据残差大小基于1个加权函数设定的,即残差越大,权重越小(Zhang et al,2003)。由图 11可见,随着迭代次数的增加,均方根残差逐渐降低。反演前、后的均方根绝对残差分别为0.914、0.570s,而对应的加权均方根残差分别为0.759、0.400s。另外,从数据残差分布来看,基于台站对波形互相关分析得到的台站对走时差数据,相对于初始模型,基本对称分布在0点的两侧(图 12)。而基于人工拾取得到的走时数据,相对于初始速度模型的残差分布不在0点两侧对称分布,而是更多地偏向于负残差部分,表明拾取的到时数据更倾向偏早于理论数据。从这点来看,基于台站对波形互相关分析得到的到时差数据更可靠。对比反演前、后台站对走时差的残差分布可以看出,反演后残差更多地聚集在0附近,表明最终得到的速度模型更好地拟合了数据。
|
图 10 在不同深度的vP成像结果(左列)以及对应的棋盘测试(右列) 从上到下深度依次为2、5、10、15km |
|
图 11 台站对走时差均方根残差(实线)、加权均方根残差(虚线)随迭代次数的变化 |

|
图 12 观测走时与理论走时的残差统计 (a)观测的绝对走时与根据初始速度模型计算的理论走时的残差;(b)观测的台站对互相关走时差与根据初始速度模型计算的理论走时差的残差;(c)观测的台站对互相关走时差与根据最终速度模型计算的理论走时差的残差 |
由速度模型可以看出,反演得到的速度模型表现出了较强的非均匀性。结合已有的区域地质资料和电磁成像结果,可以对该速度模型进行初步的解释。在2km深的P波速度水平切片中的低速异常区(图 10中A、B处)位于已发现温泉的区域附近,例如A处有舒城西汤池温泉,B处有巢湖半汤温泉,意味着这些低速异常区可能是由于裂缝和流体的存在所致。B处的低速异常区域在深部至少延伸到10~15km(图 10中G处),表明在深部可能存在高温异常而导致低速异常。5km深P波速度水平切片中的高速异常(图 10中C处)位于庐枞火山岩盆地中燕山期中性侵入岩体附近(安徽省地质矿产局,1982),因此该高速异常很可能是由侵入岩体造成的。长江下游地区MT-AB剖面和长江下游地区MT-CD剖面2条综合解释剖面图资料揭示,该处深1~7km处有1个半径25~30km的近圆形高阻异常区,异常区电阻率大于1000Ω·m,异常中心电阻率可达4000Ω·m,推测为下古生界碳酸盐岩(可能有岩体)①。该高速、高阻异常很可能是导致图 4所示的Pg波时-距曲线在震中距90km左右出现斜率明显变化的原因。在10、15km深的P波速度水平切片中可以看出,金寨-西汤池断裂(F1) 位于高速与低速的分界处,大别山地区为低速异常(图 10中D处),而F1断裂北侧,即北淮阳弧后盆地附近属于华北板块南端为高速异常(图 10中F处)。而10km深P波速度高速异常(图 10中E处)位于无为沉积断陷盆地东侧附近,对应着基于长江中下游地区MT-073剖面资料得到的电阻率大于700Ω·m的高阻异常区域①。由于本文研究仅利用了庐江台阵的数据,目的是研究基于气枪主动源的台站对的走时差数据,同时也对速度模型进行了有效的成像。但是由于受数据覆盖的限制,对整个区域速度模型的空间分辨率仍显不够。下一步工作计划综合研究长江安徽段气枪主动源收集的所有数据,以获得安徽及邻区更高分辨率的速度模型。
① 刘双庆等, 2009, 安徽省沿江地区资料2次开发研究成果报告。
5 结论利用布设的庐江地震台阵,我们记录了长江安徽段主动源实验的数据,并进行了线性和相位加权叠加处理。结果发现,相位加权叠加之后波形数据信噪比更高,但同时对绝对到时的拾取存在较大误差。为此,本文提出基于台站对波形互相关的方法,该方法可以较准确地计算台站对的走时差。同时发现,依据新发展的台站对双差地震成像算法,直接利用台站对走时差确定台阵附近浅部的速度结构,得到的速度模型与区域地质结构吻合较好,表明基于台站对双差走时成像算法可以更有效地利用主动源气枪数据研究地下结构分布。
| 安徽省地质矿产局. 1982, 安徽省区域地质志. 北京: 地质出版社. |
| 陈颙, 王宝善, 葛洪魁, 等. 2007, 建立地震发射台的建议. 地球科学进展, 22(5): 441–446. |
| 江国明, 张贵宾, 徐峣. 2012, 远震相对走时数据快速计算方法及应用. 地球物理学报, 55(12). DOI:10.6038/j.issn.0001-5733.2012.12.037 |
| 林建民, 王宝善, 葛洪魁, 等. 2008, 大容量气枪震源特征及地震波传播的震相分析. 地球物理学报, 51(1): 206–212. |
| 唐杰, 王宝善, 葛洪魁, 等. 2009, 大容量气枪震源的实验与模拟研究. 中国地震, 25(1): 1–10. |
| 杨微, 王宝善, 葛洪魁, 等. 2009, 大容量气枪震源主动探测技术系统及试验研究. 中国地震, 29(4): 399–410. |
| Aster R C, Borchers B, Thurber C H. 2013, Parameter estimation and inverse problems. Academic Press |
| Rawlinson N, Kennett B L N. 2004, Rapid estimation of relative and absolute delay times across a network by adaptive stacking. Geophys J Int, 157: 332–340. DOI:10.1111/gji.2004.157.issue-1. |
| Schimmel M, Hanneke P. 1997, Noise reduction and detection of weak. Geophys J Int, 130: 497–505. DOI:10.1111/gji.1997.130.issue-2. |
| Schimmel M, Stutzmann E, Gallart J. 2011, Using instantaneous phase coherence for signal extraction from ambient noise data at a local to a global scale. Geophys J Int, 184: 494–506. DOI:10.1111/gji.2010.184.issue-1. |
| Shen W, Ritzwoller M H, Kang D, et al. 2016, A seismic reference model for the crust and uppermost mantle beneath China from surface wave dispersion. Geophys J Int, submitted. |
| Zhang H J, Nadeau R M, Guo H. 2016, Imaging the Nonvolcanic Tremor zone beneath the San Andreas Fault at Cholame, California using station-pair double-difference tomography. Geophys Res Lett, submitted. |
| Zhang H J, Nadeau R M, Toksoz M N. 2010, Locating nonvolcanic tremors beneath the San Andreas Fault using a station-pair double-difference location method. Geophys Res Lett, 37: L13304. DOI:10.1029/2010GL043577. |
| Zhang H J, Thurber C H. 2003, Double-difference tomography:The method and its application to the Hayward fault, California. Bull Seism Soc Am, 93(5): 1875–1889. DOI:10.1785/0120020190. |
| Zhang H J, Thurber C H. 2006, Development and applications of double-difference seismic tomography. Pure Appl Geophys, 163(2-3): 373–403. DOI:10.1007/s00024-005-0021-y. |
 2016, Vol. 32
2016, Vol. 32



