安徽人工震源地下结构探测科学实验是在地学长江计划的统一平台下,以长江流域安徽段为先期实验区,在长江航道中激发气枪震源,通过周边300km范围以内的固定地震台以及三维流动观测系统接收人工地震波信号,进行长江两岸地下结构探测,获取地下三维结构模型,对该区域特殊的构造环境、成矿带的形成机制和巨型平移断裂的端部效应等相关问题进行研究①。
① 陈涛, 2015, 长江流域安徽段人工震源地下结构探测科学实验简介,http://www.cea.gov.cn/publish/dizhenj/121/379/20150917154613397737090/index.html
安徽省位于华北块体与扬子地块碰撞耦合区,是华北块体、秦岭-大别造山带与扬子块体交汇的区域。在秦岭-大别造山带与切穿地壳的郯庐断裂带交汇的前陆,以长江为中线,南北各50~100km范围内形成了南西狭窄、北东宽阔的V字型长江中下游成矿带(常印佛等,1991)(图 1)。受中晚侏罗世-早白垩世古太平洋板块的NW向低角度俯冲的远程挤压应力作用带来的陆内造山运动,及其后伴随着大规模火山-岩浆侵入作用的伸展作用的影响,长江中下游成矿带形成了隆升(铜陵、宁镇、贵池等矿集区)与坳陷(宁芜、庐枞等矿集区)相间的构造格局(常印佛等,1991;吕庆田等,2014)。长江中下游成矿带西北紧邻安庆地区的崆岭-董岭地体,东南与江南地体相接,因此,扬子块体“一盖多底”的特征(常印佛等,1996)在该区域上地壳有集中体现。
|
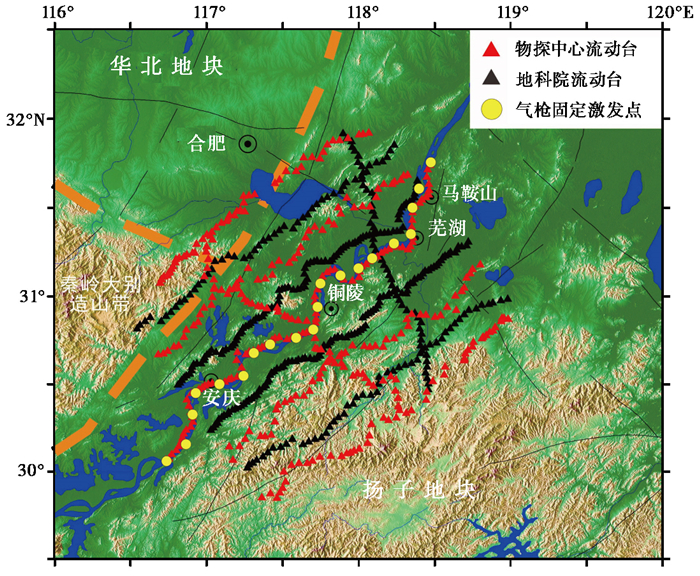
图 1 安徽实验三维探测观测系统 |
初至波走时成像是获得高分辨上地壳速度结构的主要手段(Zelt et al,1998;段永红等,2002;徐朝繁等,2006;潘继顺等,2008;贾宇鹏等,2012)。地学长江计划安徽段实验获得的沿长江高分辨探测剖面,对长江中下游成矿带及安庆地区的崆岭-董岭地体形成了密集的上地壳观测,为研究该区域地壳结构、构造演化及成矿机制等提供了良好的数据。
1 观测与数据地学长江计划安徽段实验在安徽境内以长江为中心,共布设平行于长江的横测线9条,近垂直于长江的测线2条,布设三分量数字地震仪超过700台,其中含350台PDS-2型数字地震仪和350台DZS-1深层数字地震仪,以及50台重庆地质仪器厂试验仪器,采样率均设定为200。观测系统如图 1所示。流动观测采用连续观测,以接收在长江内激发产生的气枪信号。为确保观测质量,全部地震仪均埋置于直径大于30cm、深度超过40cm的基准坑内,部分区域架设了台基并进行了防水处理。
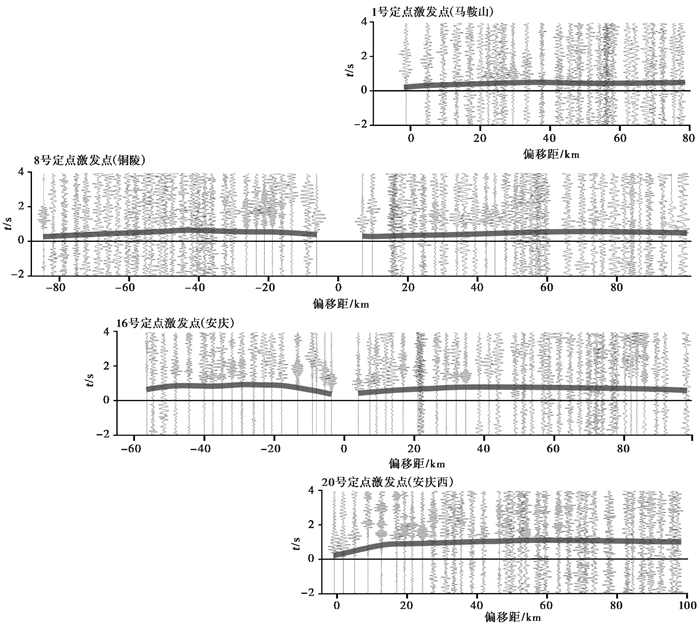
本文以沿长江布设的测线观测到的20次定点激发数据为研究对象。该测线共布设仪器100台,平均观测点距2km。20次定点激发产生的数据通过线性叠加(Wang et al,2012)的方法提取微弱信号,最终获得20张共2000道叠加记录。典型记录截面为第16个定点激发点获取的叠加记录(图 2)。所有记录经3~8Hz带通滤波后拾取初至Pg震相并获取震相拾取误差,震相拾取误差均值为100ms。Pg到时可追踪距离为60~85km。
|
图 2 定点激发点叠加记录截面 纵轴为速度6km/s的折合走时 |
正则化方法是解病态方程组时在数据之外引入一些约束条件来处理解的欠定部分或防止数据过度拟合的情况。这些约束条件通常是对解的复杂性的惩罚性措施,如成像中的平滑度控制。因此,正则化过程在一定程度上可视为反演走时曲线而非拟合单点走时(Zhang et al,1998)。由此,可构造包含速度模型平滑度和数据拟合度的目标函数(Zelt et al,1998)
| $ \mathit{{{\varPhi} }}\left( \mathit{\boldsymbol{m}} \right) = {\rm{ \mathsf{ δ} }}{t^T}\mathit{\boldsymbol{C}}_{\bf{d}}^{^{ - 1}}{\rm{ \mathsf{ δ} }}t + \lambda [{\mathit{\boldsymbol{m}}^T}\mathit{\boldsymbol{C}}_{\bf{h}}^{^{ - 1}}\mathit{\boldsymbol{m + }}{s_{\rm{z}}}{\mathit{\boldsymbol{m}}^T}\mathit{\boldsymbol{C}}_{\bf{v}}^{ - 1}\mathit{\boldsymbol{m}}{\rm{]}} $ | (1) |
m为模型矢量;δt为数据残差;Cd为数据协方差矩阵;Ch和Cv分别为水平、垂向平滑度矩阵;λ为数据拟合与模型平滑度协调因子;sz为垂向平滑度权重因子,协调其与水平平滑度的权重。于是,每1次的线性迭代问题可归结为求解1个δm,使得目标函数最小(Zelt et al,1998)
| $ \left[ \begin{array}{l} \mathit{\boldsymbol{C}}_{\bf{d}}^{^{ - 1/2}}\mathit{\boldsymbol{L}}\\ \lambda {\mathit{\boldsymbol{C}}_{\bf{h}}}\\ {s_{\rm{z}}}\lambda {\mathit{\boldsymbol{C}}_{\bf{v}}} \end{array} \right]{\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{m}} = \left[ \begin{array}{l} \mathit{\boldsymbol{C}}_{\bf{d}}^{^{ - 1/2}}{\rm{ \mathsf{ δ} t}}\\ - \lambda {\mathit{\boldsymbol{C}}_{\bf{h}}}{m_0}\\ - {s_{\rm{z}}}{\mathit{\boldsymbol{C}}_{\bf{v}}}{m_0} \end{array} \right] $ | (2) |
L为目标函数偏导数矩阵;m0为当前模型;δm为待求模型扰动;新模型矢量m=m0+δm。式(2) 可用LSQR算法求解。
由于上述正则化算法同时引入了水平、垂向扰动因子,使纵向分辨率有较大提高,采用横向、纵向不同宽度的网格,同时合理选取正则化因子,则可以对剖面上部分无射线覆盖区较好地给出合理的平滑解,最终得到整个研究区在横向、纵向较合理的最小格点最平滑解(Zelt et al,1998)。
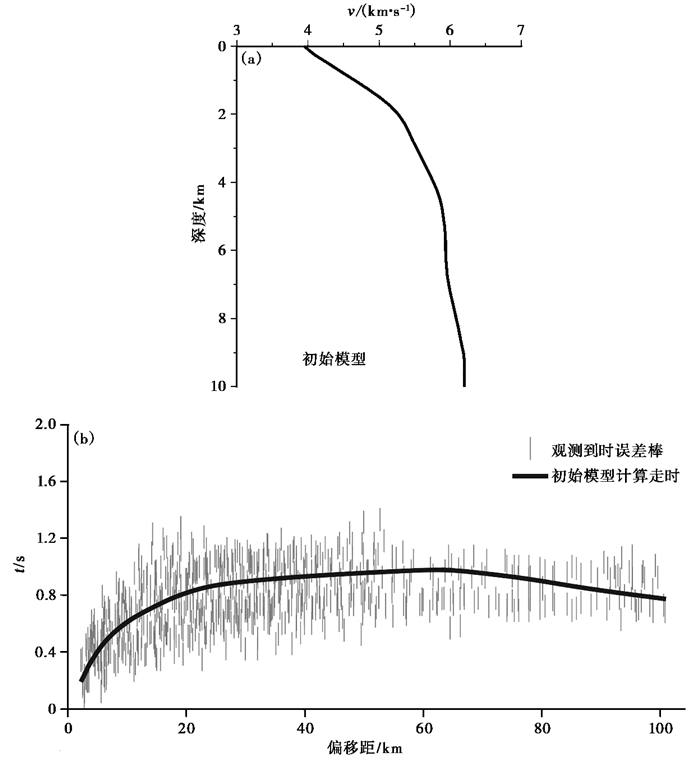
2.1 初始模型的选取对于初至波走时成像,合理而客观的初始模型应该是一个纵向速度梯度的分布符合研究区地壳速度梯度的一维模型(Zelt et al,1998)。本文采用多次成像尝试法获得了最佳一维平均模型作为初始模型(Zelt et al,2003),初始模型如图 3(a)所示。图 3(b)为初始模型计算走时与观测走时的对比。由图 3(b)可见,初始模型计算所得走时曲线通过了观测走时簇中央,故该模型较为合理。
|
图 3 初始模型(a)及初始模型计算走时与观测走时对比(b) 纵轴为速度6km/s的折合走时 |
正演算法采用二阶有限差分算法求解程函方程的波前算法(Hole et al,1995;Zelt et al,1998),正演模型采用0.25km×0.25km对研究区进行网格化,最终正演格点为水平向1081个,垂向41个,共计44321个节点。
反演网格采用1.00km×0.25km,即水平方向网格点间距为1000m,深度方向网格点间距为250m,形成水平向网格270个,垂向网格40个,共计反演网格10800个,水平与垂向平滑权重因子sz取值为0.15。
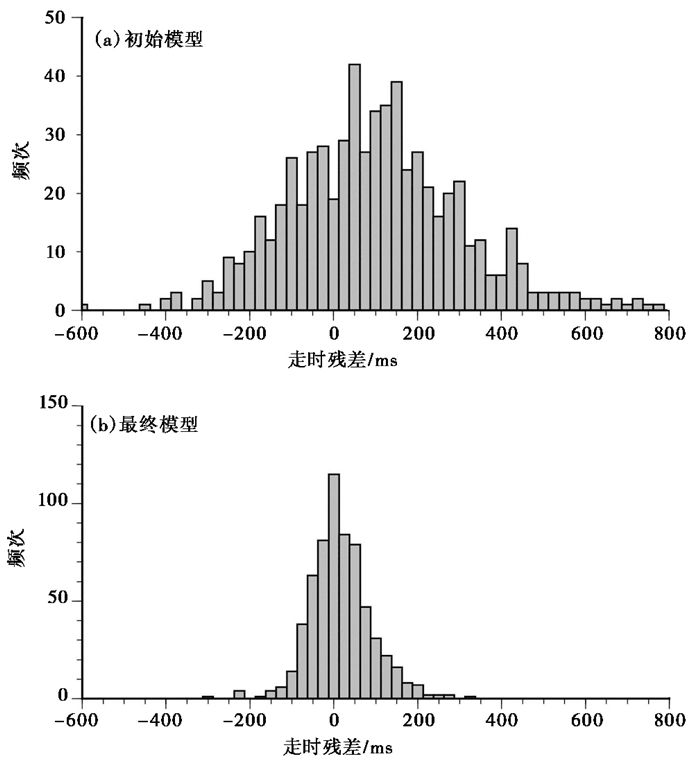
2.3 数据拟合误差与稳定性分析初始模型射线追踪均方根残差为198ms,χ2值为6.13。阻尼因子下降速率为每10次迭代降低100,通过58次迭代,最终均方根残差达到80ms,χ2降低为1。初始模型和最终模型走时残差分布如图 4所示,由图 4可见,初始模型走时拟合误差范围为±0.6s,最终模型走时拟合残差误差范围约束在±0.1s以内,与震相拾取误差一致,且与χ2值为1相对应,因此本次反演数据无过度拟合,也无拟合不足。
|
图 4 反演前(a)、后(b)走时残差分布 |
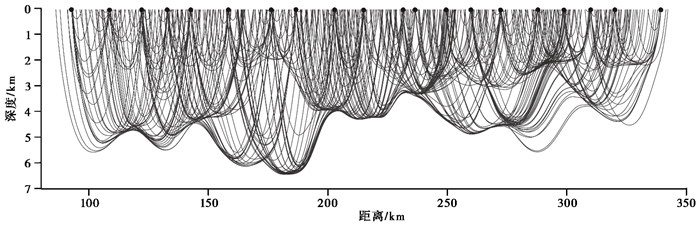
最终模型射线覆盖如图 5所示,由图 5可见,共计射线628条,对研究区上地壳形成了较好的覆盖,说明该成像结果稳健可靠。
|
图 5 马鞍山-铜陵-安庆上地壳射线覆盖 |
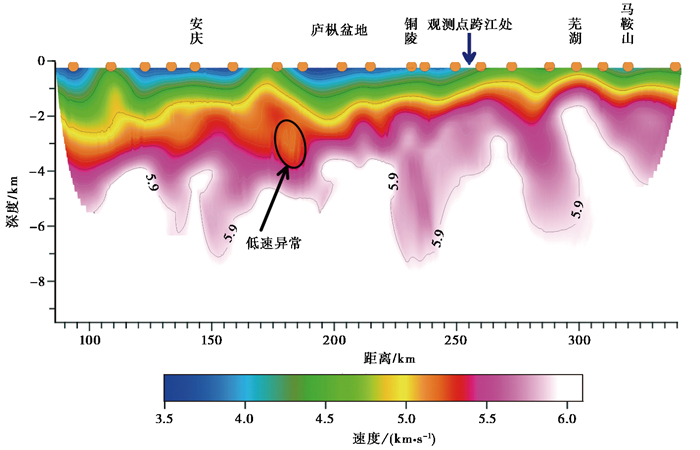
图 6为马鞍山-铜陵-安庆上地壳速度结构模型。由图 6可见, 该区域结晶上地壳结构横向差异明显,具有典型的分区特征。
|
图 6 马鞍山-铜陵-安庆上地壳速度结构 |
庐枞盆地以西的安庆一带,基底埋深较大,为4~6km,上地壳为典型的两隆两坳相间的构造特征,该区测点位于长江北岸,具有较厚的沉积层覆盖,地表速度约3.5km/s,地表表现为大面积的冲积平原。
庐枞盆地结晶基底埋深4~5km,沉积盖层呈明显的坳陷盆地形态,显示了中生代以来经历的伸展坳陷过程。庐枞盆地地表速度为3.5~4.0km/s,在庐枞盆地边缘3km左右埋深处存在明显的低速异常,可能与中生代以来所经历的火山-岩浆活动有关,暗示了其基底坳陷型火山盆地的特点。庐枞盆地内部埋深浅于3km的低速介质,结合在贵池区域开展的深地震反射和MT成像结果考虑,这可能对应了该区域残留的岩浆活动通道(董树文等,2010)。
测点在铜陵以东跨过长江,置于长江南岸观测,观测点跨江处近地表存在明显的速度横向变化。跨江后地表速度迅速提升,约为4.5km/s,沉积盖层明显上隆,基底埋深2~4km。铜陵以东至芜湖沉积盖层呈明显的隆升特征,与该区域开展的深地震反射显示的上地壳复杂的户型反射相应(吕庆田等,2002),推测为褶皱、冲断和侵入构造,表明上地壳发生了强烈挤压变形。
致谢: 感谢张先康研究员对本次实验数据处理的指导性建议,感谢王宝善研究员、姚华建教授对气枪震源数据处理的支持和帮助。| 常印佛, 董树文, 黄德志. 1996, 论中下扬子"一盖多底"格局与演化. 火山地质与矿产, 17(增刊Ⅰ): 1–15. |
| 常印佛, 刘湘培, 吴言昌. 1991, 长江中下游铁铜成矿带. 北京: 地质出版社: 1-239. |
| 段永红, 张先康, 方盛明. 2002, 华北地区上部地壳结构的三维有限差分层析成像. 地球物理学报, 45(3): 362–369. |
| 董树文, 项怀顺, 高锐, 等. 2010, 长江中下游庐江-枞阳火山岩矿集区深部结构与成矿作用. 岩石学报, 26(9): 2529–2542. |
| 贾宇鹏, 王夫运, 田晓峰, 等. 2012, 天津-北京高分辨地震折射剖面初至波走时成像. 西北地震学报, 34(4): 375–382. |
| 吕庆田, 董树文, 史大年, 等. 2014, 长江中下游成矿带岩石圈结构与成矿动力学模型——深部探测(SinoProbe)综述. 岩石学报, 30(4): 889–906. |
| 吕庆田, 黄东定, 侯增谦, 等. 2002, 铜陵矿集区地壳结构的深地震反射成像. 矿床地质(增刊Ⅰ): 1173–1176. |
| 潘纪顺, 张先康, ZhaoPing, 等. 2008, 2D多尺度非线性地震速度成像. 地球物理学报, 51(1): 197–205. |
| 徐朝繁, 张先康, 张建狮, 等. 2006, 射线数分布分析法及其在地壳上部复杂结构探测中的应用. 地震学报, 28(2): 167–175. |
| Hole J A, Zelt B C. 1995, 3-D finite-difference reflection travel times. Geophys J Int, 121: 427–434. DOI:10.1111/gji.1995.121.issue-2. |
| Wang B S, Ge H K, Yang W, et al. 2012, Transmitting seismic station monitors fault zone at depth. Eos Transactions American Geophysical Union, 93(5): 49–50. |
| Zelt C A, Barton P J. 1998, 3D seismic refraction tomography:A comparison of two methods applied to data from the Faeroe Basin. J Geophys Res, 103: 7187–7210. DOI:10.1029/97JB03536. |
| Zelt C A, Sain K, Naumenko J V, et al. 2003, Assessment of crustal velocity models using seismic refraction and reflection tomography. Geophys J Int, 153: 609–626. DOI:10.1046/j.1365-246X.2003.01919.x. |
| Zhang J, Toksoz M N. 1998, Nonlinear refraction travel time tomography. Geophysics, 63(5): 1726–1737. DOI:10.1190/1.1444468. |
 2016, Vol. 32
2016, Vol. 32


