2014年8月3日16时30分,云南省昭通市鲁甸县(27.1°N,103.3°E)发生MS6.5地震,震源深度12km。此次地震是发生在NE向昭通-鲁甸断裂系NW向次级走滑断层包谷垴-小河断裂上的高倾角左旋走滑地震(http://www.cea.gov.cn/publish/dizhenj/468/553)。地震较大的滑动量集中于浅部,大部分深度小于10km,且加权震源深度仅为8km。地震诱发了大量的次生灾害,造成了严重的人员伤亡。
鲁甸MS6.5地震发生后,中国地震局地球物理研究所无人机灾情快速获取组于8月5~7日执行了8个架次、270km总里程的极震区航拍任务,获取了包含大量灾情信息(房屋倒塌、山体崩塌、道路阻塞、滑坡、堰塞湖等)、分辨率为0.3m的原始图像4095张,并快速完成了航拍区二维影像的拼合(图 1)。航拍影像至少覆盖了鲁甸县3个乡镇(乐红镇、龙头山镇、火德红乡等)的9个行政村(官寨村、翠屏村、龙泉村、八宝村、光明村、龙井村、李家山村、银厂村、机车村等)约207km2的区域。作为一种便捷、安全、高精度的新型灾情获取技术,无人机灾情快速获取为地震现场的应急救援以及震后的灾情分析提供了重要的影像资料(徐志强等,2012)。

|
图 1 航拍灾情展示 (a)王家坡滑坡造成房屋被埋;(b)苗寨子滑坡造成昭巧公路堵塞;(c)红石岩堰塞湖引起牛栏江上游水位上涨淹没沿岸的田地和村庄;(d)Ⅷ度区民房的典型破坏情况;(e)龙头山镇镇政府驻地的航拍影像拼合图 |
利用由灾情快速获取技术获得的资料,通过模型回归方法进行的震后灾害(尤其是次生地质灾害如崩塌滑坡等)分析,一方面可快速提供震区灾害的理论分布状况,为地震现场的应急工作提供参考,另一方面对探究灾害的成因、预判地震危险区的灾害发生趋势等亦具有重要意义。
本文利用航拍影像并结合鲁甸地区的地质资料,探究航拍区内由鲁甸MS6.5地震诱发的崩塌滑坡的空间分布特征,通过M5′模型树算法建立崩塌滑坡分布特征与其影响因子间的量化模型。
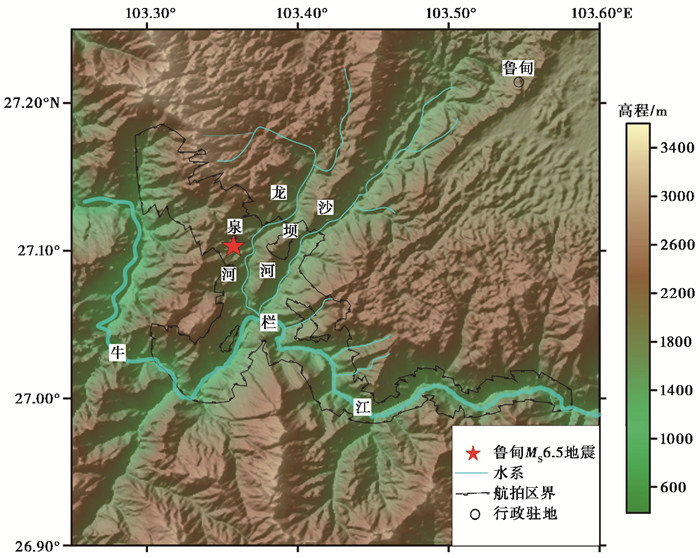
1 研究区概况 1.1 地貌航拍区位于鲁甸县西南部,以深切割中山区中构造溶蚀侵蚀高山峡谷地貌为主,平均海拔为1000~3000m,该地貌山顶与谷底高差达1km以上,容易在谷底下段形成坡脚超过50°的窄带形谷或障谷;航拍区内主要有牛栏江、沙坝河、龙泉河等3条河流,它们同属金沙江下游水系,大部分河道呈陡壁,顶端略开阔,谷坡范围为30°~40°(云南省鲁甸县志编纂委员会,1995)(图 2)。
|
图 2 鲁甸地震震中、航拍区主要水系分布及航拍区界示意图 |
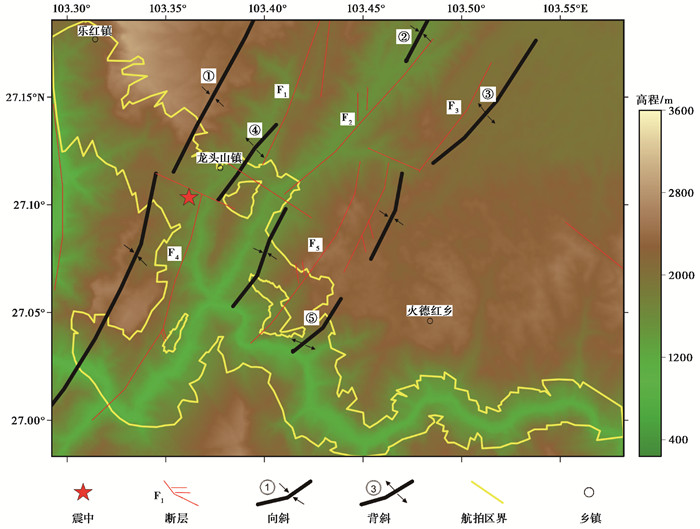
鲁甸县位于川滇经向构造体系绿汁江-小江南北构造带东缘与其东侧川滇多字型构造结合部位。航拍区位于骡马口构造带,断层和褶曲(表 1)为形成该构造带的主要体系(图 3)。骡马口断层与鲁甸断层等与其平行的断层组合成为骡马口断裂带,该断裂带为控制鲁甸地区地质构造发展的明显因素,区域内最大褶曲构造为阿鲁块向斜,其沿经向贯穿鲁甸全县①。
| 表 1 航拍区构造成分及编号 |
|
图 3 航拍区及周边地区的主要断层和褶曲分布 |
① 云南省地质局第二区域地质调查队, 1976, 1 ︰ 20万鲁甸幅区域地质调查报告
1.3 气候、植被条件鲁甸境域属低纬度山地季风气候,四季温差不大,立体气候特点突出,年平均气温12.1℃,年平均降雨量923.5mm。由于受自然条件及人为开垦等因素的影响,鲁甸全县植被覆盖率较低,航拍区只有火德红乡与龙头山镇交界的部分区域、龙头山镇翠屏村附近等极小区域的植被覆盖率大于25%。
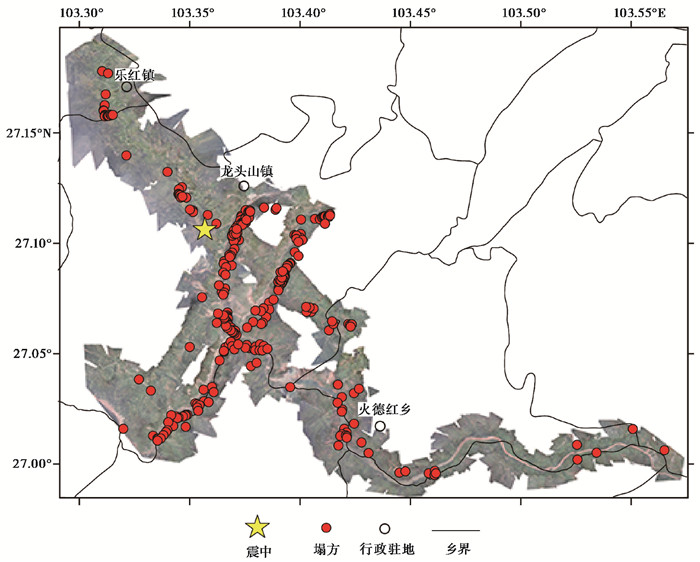
2 崩塌滑坡的空间分布及其影响因素分析极震区复杂的地形条件极大地影响了震后灾情的获取效率,为此,本研究直接将航拍影像的拼合图、原始照片与卫星影像进行对比,判读出位于极震区、面积超过50m2的崩塌滑坡共287处,利用地震现场指挥调度平台获得了塌方的经纬度(图 4)。由图 4可见,鲁甸县龙头山镇翠屏村、龙井村、龙泉村的崩塌滑坡最为密集且多沿河流、道路、沟谷排布形成条带交错走势。为了建立能够反映崩塌滑坡分布特征的回归模型,我们分析了影响其分布的主要因素。
|
图 4 航拍区崩塌滑坡分布 |
(1) 震中距或断层距。地震是航拍区产生崩塌滑坡的诱发因素,因此,崩塌滑坡分布特征会随震中距或活动断层距的变化而出现差异。Wang等(2008)在研究日本新潟地震引发的滑坡的空间分布规律时认为,震中距与滑坡的分布间存在衰减关系;然而张建强等(2013)在对芦山地震崩塌滑坡与公路危险性进行评价时并未得出这样的关系,他们认为是研究区范围过小、距震中较近以及其他近场因素等共同作用的结果。本研究所面临的状况与张建强等(2013)的类似,因此,在本研究中将以断层距为影响因子,以期从另外一个角度探寻地震因素与崩塌滑坡分布间的关系。
(2) 坡度和坡向。地形地貌、岩土体结构作为崩塌滑坡产生的地质条件,对崩塌滑坡的空间分布会产生很大影响。坡度和坡向是描述地形因素的2个基本因子,其中,对崩塌影响最大的是坡度因子(Meunir et al,2008);岩土体结构中破碎、松散软弱、完整性差的岩土体有利于崩塌的形成。航拍区岩土体类型包括块体碎裂结构、构造碎裂结构、层状结构、层块结构、层状夹软结构、块体溶蚀结构等。不同岩土体结构的层面特征差异较大,力学强度与稳定性也不相同。
(3) 植被条件。植被具有保持水土、抑制水力侵蚀、提高边坡稳定性的作用,若植被发育,则可削弱水土流失和崩塌流活动;反之,植被稀少,岩石裸露,水力侵蚀活动加剧,岩石风化严重,势必导致崩塌现象加剧。因此,植被条件也是影响崩塌滑坡分布特征的重要因素。
考虑到航拍区域面积相对较小,具有大尺度特征且对于分析崩塌滑坡分布规律而言作用不大的因素对于本研究并没有很大的实际意义,因此,通过权衡各因素对崩塌滑坡分布的可能影响程度以及各因素自身的分布特征,将活动断层距、坡度、岩土体结构、植被条件等确定为基本影响因素。
3 利用M5′模型树算法建模 3.1 算法针对已确定的影响崩塌滑坡分布的基本因素,我们利用M5′模型树算法进行回归建模。M5′模型树算法是Wang等(1997)在Quinlan(1992)提出分段式多元线性回归树(M5模型树)理念之后建立起来的一种具有较高精度的一阶线性模型树算法。该算法先根据样本属性差异化原则对样本空间实现细化分裂,直到满足分裂至某一结点处的样本数少于一定数量或者结点样本属性标准差小于某一限定值的条件时,分裂结束。样本属性差异化原则可表示为
| $ {S_{{\rm{DR}}}} = {\rm{sd}}\left(T \right) - \sum\nolimits_{_i} {\frac{{|{T_i}|}}{{|T|}} \times {\rm{sd}}({T_i})} $ | (1) |
式中,T为达到某一结点的样本总集合;Ti为将T分裂为i个空间后的第i个样本集合,sd(Ti)为样本集合的属性标准差。这一过程相当于模拟树生长的过程对所有样本进行细化分类后产生1个初始模型树,模型树停止生长的结点即分裂结束的结点称为叶子结点。对每一个子结点利用线性回归方法建立1个多元回归方程,最终得到线性模型。
为了提高整个模型的应用效率,需要通过剪枝过程遍历初始模型树的每一个结点对某些子树进行归并而以叶子结点取代。遍历结点时,首先利用线性回归方法拟合出结点的多元线性方程,然后以预测误差的减小量为剪枝的标准来决定是否应保留结点的子树或将该子树转变为1个叶子结点。预测误差的减小量可表示为
| ${E_{\rm{R}}} = |N|{R_{{\rm{MSE}}}} - |{N_{\rm{l}}}|{R_{{\rm{MS}}{{\rm{E}}_{\rm{l}}}}} - |{N_{\rm{r}}}|{R_{{\rm{MS}}{{\rm{E}}_{\rm{r}}}}} $ | (2) |
式中,RMSE为某一结点(包括下属子树和叶子的所有样本)拟合方程预测的均方根误差,RMSEl、RMSEr为该结点左、右叶子结点的预测均方根误差。当ER为正值时,保留子树;否则,将其转变为1个叶子节点。
经过剪枝上述递归的处理过程,初始模型树优化成具有最简结构的模型树。但是,模型树相邻叶子结点的线性模型可能会产生一定程度的不连续性,这将会导致模型分段点处的非线性,从而影响模型预测精度。因此,模型树的平滑过程中将每一结点的子结点与其父结点的2个多元线性拟合方程通过下式合并为1个新的线性方程,从而有效地减小了由剪枝过程带来的上述负面效应(章坚民等,2011)
| $ {f_n} = \frac{{n{f_{\rm{c}}} + k{f_{\rm{p}}}}}{{n + k}} $ | (3) |
式中,fp为父结点拟合方程;fc为子结点拟合方程;n为到达叶子结点的样本数;k为常值(一般取为15);fn为合并的方程。当子结点采用新函数后,RMSE变化小于一定阀值时,将取代子结点的线性方程;否则,则不进行平滑处理。
近年来,M5′模型树算法已被广泛应用于计算机工程(王涛,2010)、化学工程与技术(Clark,2010)、水利工程(Etemad et al,2009;Sattari et al,2013)等领域的数据处理与回归建模过程中。
3.2 变量的量化处理用于建立量化模型的变量有5个,即崩塌滑坡分布特征、断层距、坡度、岩土体结构类型、植被条件等。其中,崩塌滑坡分布特征为因变量,其他4个因子为自变量。建立量化模型就是寻求因变量与自变量之间的数值关系,其最基本的要求就是所有变量类型为数值型,因此,需要根据回归建模的需求对这5个变量进行量化处理。
首先,利用以各崩塌滑坡点为中心建立的固定大小的矩形网格内的崩塌滑坡个数来量化崩塌滑坡分布特征,其描述了单位网格内崩塌滑坡分布的密集度。网格大小的划分以不扭曲崩塌滑坡分布空间特征、不割裂地质现象为依据(胡金等,2008),本文将包含整个航拍区的矩形范围划分为20个等面积矩形网格单元,统计每个网格单元内的崩塌滑坡数作为崩塌滑坡分布的量化表达。
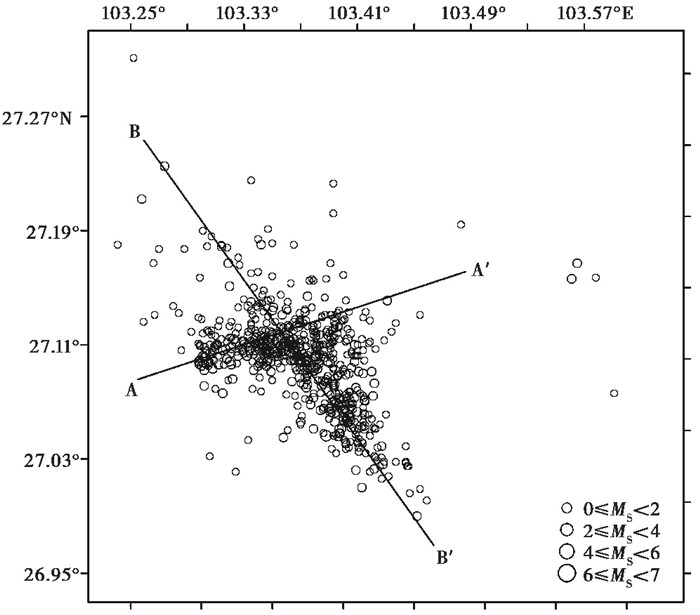
其次,考虑断层距的量化表达。由余震精定位结果可知,鲁甸地震的余震在NNW-SSE、ENE-WSW两个方向上都有一定尺度的延伸(王未来等,2014;张广伟等,2014),这表明此次地震的发震构造和破裂过程可能具有一定的复杂性。烈度分布和破裂过程反演等研究都更倾向于近SN向的小河-包谷垴断裂是此次地震的发震构造(徐锡伟等,2014;张勇等,2014;刘成利等,2014)。而视震源时间函数分析表明,鲁甸地震可能为共轭断层先后破裂的结果(许力生等,2014)。另外,张广伟等(2014)根据余震分布和震源机制解的结果也提出可能存在共轭破裂的情况。张勇等(2014、2015) 对鲁甸地震破裂过程进行了反演,认为鲁甸地震是由2条共轭断层先后破裂引发的,这2条共轭断层线的位置与余震条带分布一致。如果综合考虑极震区余震的密集分布和主震破裂对崩塌滑坡的影响,则利用共轭的断层模型来计算断层距比较可靠。因此,我们将余震精定位后确定的2条共轭的余震分布条带(王未来等,2014;张广伟等,2014;房立华等,2014)作为活动断层线(图 5),计算了每个崩塌滑坡点与2条断层线之间的距离,选择距离较近者作为断层距参数。
|
图 5 鲁甸地震余震分布 AA′和BB′为2条共轭的余震分布延伸条带 |
此外,以grd格式的规则网格化地形数据为基础,计算每个崩塌滑坡点的坡度信息。地表某点的坡度定义为过该点的切平面与水平面的夹角,描述了地表面在该点的倾斜程度。基于规则格网的坡度Slope可表示为
| $ {\rm{Slope}} = \sqrt {{\rm{Slope}}_{_{{\rm{we}}}}^{^2} + {\rm{Slope}}_{_{{\rm{sn}}}}^{^2}} $ | (4) |
Slopewe为经向坡度
| $ {\rm{Slop}}{{\rm{e}}_{{\rm{we}}}} = \frac{{({e_8} + 2{e_1} + {e_5}) - ({e_7} + 2{e_3} + {e_6})}}{{8 \times {\rm{cellsize}}}} $ | (5) |
Slopesn为纬向坡度
| $ {\rm{Slop}}{{\rm{e}}_{{\rm{sn}}}} = \frac{{({e_7} + 2{e_4} + {e_8}) - ({e_6} + 2{e_2} + {e_5})}}{{8 \times {\rm{cellsize}}}} $ | (6) |
其中,e1,e2,e3,e4,e5,e6,e7,e8为每个格网中心点的高程(图 6)。
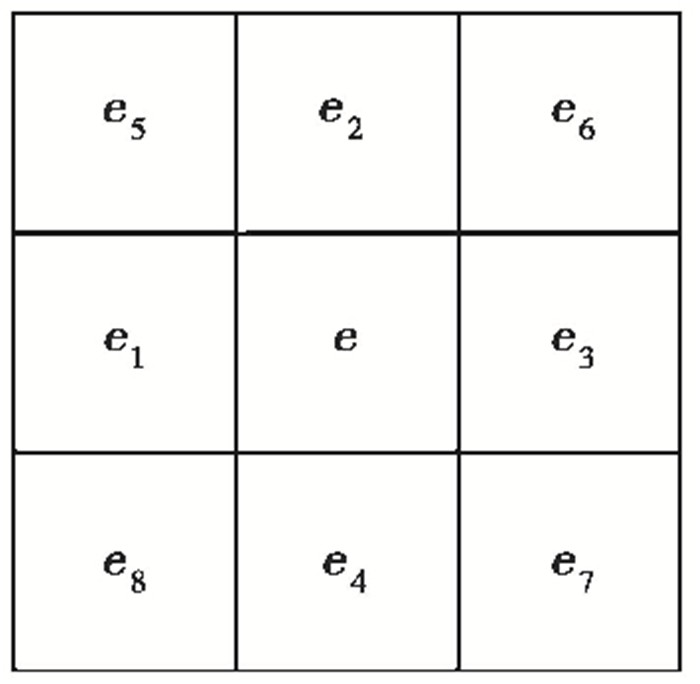
|
图 6 计算坡度的网格示例 |
根据计算得到的坡度数据简单分析了航拍区不同坡度范围内的崩塌滑坡分布特征后发现(图 7),崩塌滑坡点的坡度多为0.337~0.841(约20°~50°),而0.673~0.841(约38.5°~50.0°)之间崩塌滑坡最多。张建强等(2009)对北川县地震诱发崩塌滑坡的敏感性进行评价时指出,崩塌滑坡的密度随坡度变化的差异较大。Miles等(2009)对洛马普利塔地震区的崩塌滑坡进行研究时发现,其坡度多为15°~35°;日本新潟县中越地震震区崩塌滑坡分布最多的坡度为35°(Wang et al,2007)。因此,坡度与地震诱发的崩塌滑坡分布间的关系可能受地域特征的影响。
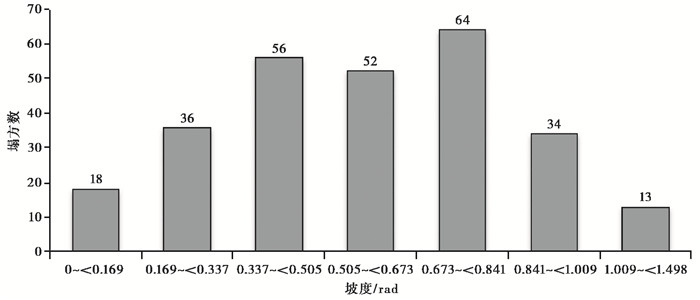
|
图 7 不同坡度范围内的崩塌滑坡数分布 |
岩土体结构的稳定性主要受层间结构面发育程度的制约,按照各岩土体结构的层间结构面发育情况将其分级作为量化该因子的标准(谭文辉等,2010),等级越大,则表示岩土体结构的稳定性越强(表 2)。
| 表 2 岩土体结构等级 |
根据航拍区植被覆盖率将植被条件量化为4个等级(表 3)。实际上,航拍区植被覆盖率大于45%的面积极少,所有崩塌滑坡均分布于前3个等级的植被条件下。
| 表 3 植被条件等级 |
航拍区范围内有15处崩塌滑坡缺乏岩土体结构以及植被覆盖率信息,因此将其剔除,最终保留273个实例作为建立量化模型的总数据集。将总数据集划分为训练数据集和测试数据集,训练数据集用于创建量化模型,测试数据集则要对量化模型的精确性进行评估。本研究采用分层随机采样的方法,按照因变量值的大小,将总数据集分为6层,按每层数据量占总数据集的比例共选取218个原始数据(约占80%)作为训练数据集,剩余的数据作为测试数据集(表 4)。
| 表 4 总数据集、训练数据集、测试数据集的统计特征 |
应用M5′模型树算法对航拍区的崩塌滑坡分布密度及其影响因子作分段线性回归,得到叶子结点数为6的模型树(图 8)。由图 8可见,岩土体结构强度、坡度以及断层距等是造成数据分裂过程非线性的主要原因,也就是说,这3个因素控制了崩塌滑坡密度的分布状况。我们在利用M5′模型树算法时,根据这3个属性将崩塌滑坡密度与其影响因子间的关系分为如下6个多元线性方程(其中,Ft为崩塌滑坡分布密度;Df为断层距;Sl为坡度;Rp为岩土体结构强度;Vg为植被条件)。当Rp≤2.5且Sl≤0.504时,线性模型为LM1,即
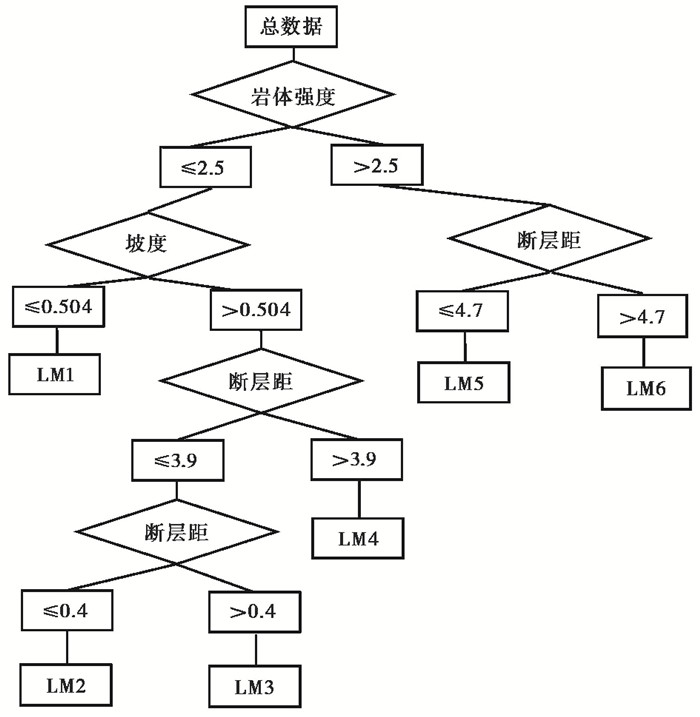
|
图 8 M5′模型树 |
| $ {F_{\rm{t}}} = - 9.2621 \times {R_{\rm{p}}} - 0.9418 \times {V_{\rm{g}}} + 3.1829 \times {S_{\rm{l}}} + 39.145 $ | (7) |
当Rp≤2.5,Sl≥0.504且Df≤0.4km时,线性模型为LM2,即
| $ {F_{\rm{t}}} = - 4.6007 \times {R_{\rm{p}}} - 0.9469 \times {V_{\rm{g}}} + 3.1829 \times {S_{\rm{l}}} + 0.0939 \times {D_{\rm{f}}} + 29.7451 $ | (8) |
当Rp≤2.5,Sl≥0.504且0.4km < Df≤3.9km时,线性模型为LM3,即
| $ {F_{\rm{t}}} = - 8.5546 \times {R_{\rm{p}}} - 0.7901 \times {V_{\rm{g}}} + 3.1829 \times {S_{\rm{l}}} - 1.909 \times {D_{\rm{f}}} + 27.4326 $ | (9) |
当Rp≤2.5,Sl≥0.504且Df>3.9km时,线性模型为LM4,即
| $ {F_{\rm{t}}} = - 1.3407 \times {R_{\rm{p}}} - 0.72351 \times {V_{\rm{g}}} + 3.1829 \times {S_{\rm{l}}} - 2.1037 \times {D_{\rm{f}}} + 35.5887 $ | (10) |
当Rp>2.5且Df≤4.7km时,线性模型为LM5,即
| $ {F_{\rm{t}}} = - 2.5218 \times {R_{\rm{p}}} + 0.123 \times {S_{\rm{l}}} - 0.9067 \times {D_{\rm{f}}} + 19.8376 $ | (11) |
当Rp>2.5且Df>4.7km时,线性模型为LM6,即
| $ {F_{\rm{t}}} = 0.7632 \times {R_{\rm{p}}} + 0.123 \times {S_{\rm{l}}} - 1.4485 \times {D_{\rm{f}}} + 24.9641 $ | (12) |
利用测试数据集对建立的分段多元线性模型进行预测实验,将预测值与实际值进行对比(图 9),计算两者的相关系数、绝对误差以作为评估模型预测性能的指标(表 5)。相关系数为
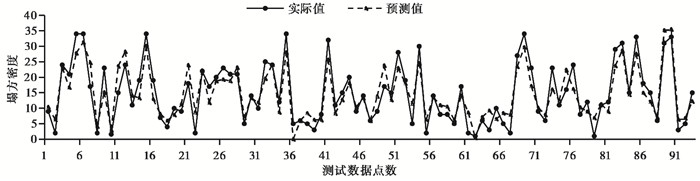
|
图 9 回归模型预测结果与实际值的比较 |
| 表 5 模型预测性能评价参数 |
| $ {C_{\rm{c}}} = \frac{{\sum {({\rm{Actua}}{{\rm{l}}_i} - \overline {{\rm{Actual}}})({\rm{Predicte}}{{\rm{d}}_i} - {\rm{Predicted}})} }}{{\sqrt {\sum {{{({\rm{Actua}}{{\rm{l}}_i} - \overline {{\rm{Actual}}})}^2}{{({\rm{Predicte}}{{\rm{d}}_i} - {\rm{Predicted}})}^2}} } }} $ | (13) |
绝对误差为
| $ {M_{{\rm{ae}}}} = \frac{1}{n}\sum\nolimits_{_{i = 1}}^{^n} {|{\rm{Actua}}{{\rm{l}}_i} - {\rm{Predicte}}{{\rm{d}}_i}|} $ | (14) |
相关系数Cc表示回归模型与真实关联函数之间的相似程度,其值越接近1,则回归模型与真实关联函数之间的差异越小;绝对误差Mae则为衡量预测值与实际值之间差异程度的指标,注重反映个体样本的预测效果。
4 分析从最终得到的分段线性回归模型来看,崩塌滑坡密度与断层距、岩土体结构强度、植被条件以及坡度分段间的线性关系比较明确,尤其是与断层距和岩土体结构强度的负相关、与坡度的正相关表现比较稳定。
考虑各自变量的量级并分析6个线性模型中各变量的系数可知,在分段线性回归模型中坡度、岩土体结构强度和断层距等对崩塌滑坡密度的变化起主控作用;由于研究区植被覆盖率普遍小于25%,而每个塌方点的植被因子差异不大,因此,回归模型中体现出植被条件对崩塌滑坡密度相对较弱的影响;当岩土体强度≤2.5km,坡度≥0.504,即岩土体结构条件为构造碎裂和块体碎裂结构、坡度≥30°时,在距断层线0.4km内,断层距与崩塌滑坡密度呈微弱的正相关,超出该范围,则这种微弱的正相关转变为负相关,并且距断层线越远,断层距对崩塌滑坡密度的影响越大。
实际上,由于受到研究对象的区域性以及各变量之间量化关系复杂性的限制,各因子与因变量之间存在复杂的非线性关系。我们在建立M5′模型树算法模型的过程中,通过剪枝与平滑这2个流程将由这一复杂的非线性关系引起的模型的不连续进行了合并与平滑处理,提高了整个模型的效率和简洁性,这一处理过程对多元分析而言是有利的。
利用M5′模型树算法建立的分段多元线性回归模型与真实关联函数之间具有较高的相关度,利用该回归模型对个体样本中崩塌滑坡密度较大的值(>9) 的预测结果比较理想,但是对样本中崩塌滑坡密度较小的值( < 4) 进行预测时效果并不好,绝对误差的大小已经与真实值相当。通过分析样本数据结构发现,总数据集中崩塌滑坡密度数值较大的样本数量多于数值较小的样本数量,这造成了数据结构在因变量值域上的不平衡,因而使模型在不同值的预测中显示出不同的效果,同时也反映了航拍区即本次地震的极震区崩塌滑坡分布具有整体密集的特点。
5 结论高精度的无人机航拍技术已经足以为震后的区域灾情分析提供可靠的影像资料,利用这些影像资料并结合卫星影像、地理空间数据等已能对灾情规模和具体位置进行评估和判断。
在鲁甸地震发生前,研究区昭巧公路、牛栏江、龙泉河以及沙坝河沿线就有崩塌滑坡的发生,在雨季尤为多见。此次从航拍影像中识别出研究区内鲁甸地震诱发的次生灾害以中小规模的崩塌滑坡为主,在空间上主要沿深切河谷分布,并且分布密度受断层距、岩土体结构、坡度、植被条件等的共同制约,其中,坡度、岩土体结构强度和断层距等为主要因素,断层距与崩塌滑坡密度间的衰减关系随断层距的增大而愈加明显;块体碎裂结构、构造碎裂结构的岩土体结构条件以及38.5°~50.0°的坡度条件更容易形成高密度的崩塌滑坡。
我们通过M5′模型树算法建立分段的线性模型来逼近航拍区崩塌滑坡密度与其影响因子之间整体上的非线性关系,最终模型突出反映了崩塌滑坡密度与各个自变量之间稳定的分段线性关系,由该算法得出的模型有助于分析多个因子对崩塌滑坡密度的综合影响,为解决震后灾害分析过程中遇到的较复杂的多元非线性问题提供了新的思路;最终模型的预测效果对于不同值域内样本数量的差异有一定的依赖性,模型检验结果显示,理论模型与实际关联函数之间的相关系数达到0.88,因此,可以利用该模型来预测鲁甸地区由地震诱发的崩塌滑坡分布。在此,我们仅仅针对鲁甸地震极震区进行了建模研究,所得模型的普遍适用性还需要进一步通过针对不同地区的灾情建模研究来检验。
| 房立华, 吴建平, 王未来, 等. 2014, 云南鲁甸MS6.5地震余震重定位及其发震构造. 地震地质, 4(4): 1173–1185. |
| 胡金, 李波, 杨艳峰. 2008, GIS在云南鲁甸县地质灾害易发形分区中的应用. 灾害学, 23(1): 73–87. |
| 刘成利, 郑勇, 熊熊, 等. 2014, 利用区域宽频带数据反演鲁甸MS6.5地震震源破裂过程. 地球物理学报, 57(1): 3028–3037. |
| 谭文辉, 蔡美峰. 2010, 边坡工程广义可靠性理论与实践. 北京: 科学出版社. |
| 王涛. 2010, M5算法在感觉评估中的应用. 微计算机信息, 33: 229–231. DOI:10.3969/j.issn.2095-6835.2010.06.093 |
| 王未来, 吴建平, 房立华, 等. 2014, 2014年云南鲁甸MS6.5地震序列的双差定位. 地球物理学报, 57(9): 3042–3051. DOI:10.6038/cjg20140929 |
| 徐锡伟, 江国焰, 于贵华, 等. 2014, 鲁甸6.5级地震发震断层判定及其构造属性讨论. 地球物理学报, 57(9): 3060–3068. DOI:10.6038/cjg20140931 |
| 徐志强, 姜旭东, 郑钰. 2012, 无人机在地震现场应用探索. 国际地震动态(6): 204–204. |
| 许力生, 张旭, 严川, 等. 2014, 基于勒夫波的鲁甸MS6.5地震震源复杂性分析. 地球物理学报, 57(9): 270–281. |
| 云南省鲁甸县志编纂委员会. 1995, 鲁甸县志. 昆明: 云南人民出版社. |
| 张广伟, 雷建设, 梁姗姗, 等. 2014, 2014年8月3日云南鲁甸MS6.5地震序列重定位与震源机制研究. 地球物理学报, 57(9): 282–291. |
| 张建强, 范建容, 严冬, 等. 2009, 地震诱发崩塌滑坡敏感性评价——以北川县为例. 四川大学学报(工程科学版), 41(3): 140–145. |
| 张建强, 苏凤环, 范建容. 2013, "4·20"芦山地震崩塌滑坡与公路危险性评价——以宝兴县省道S210沿线为例. 山地学报, 31(5): 616–623. |
| 张勇, 陈运泰, 许力生, 等. 2015, 2014年云南鲁甸MW6.1地震:一次共轭破裂地震. 地球物理学报, 58(1): 153–163. DOI:10.6038/cjg20150113 |
| 张勇, 许力生, 陈运泰, 等. 2014, 2014年8月3日云南鲁甸MW6.1(MS6.5) 地震破裂过程. 地球物理学报, 57(9): 3052–3059. DOI:10.6038/cjg20140930 |
| 章坚民, 刘登涛, 吴光中, 等. 2011, 采用M5'模型树和测量数据识别抽泣式机组汽耗量特性. 中国电机工程学报, 31(23): 21–26. |
| Clark E T, 2010, Refrigerant leak detection system and method, Patent Application, 12/943, 626. |
| Etemad S A, Mahjoobi J. 2009, Comparison between M5' model tree and neural networks for prediction of significant wave height in Lake Superior. Ocean Engineering, 36(15): 1175–1181. |
| Meunir P, Hovius N, Haines H J. 2008, Topographic site effects and the location of earthquake induced landslides. Earth and Planetary Science Letters, 275: 221–232. DOI:10.1016/j.epsl.2008.07.020. |
| Miles S B, Keefer D K. 2009, Evaluation of CAMEL-comprehensive areal model of earthquake-induced landslides. Engineering Geology, 104: 1–15. DOI:10.1016/j.enggeo.2008.08.004. |
| Quinlan R J. 1992, Learning with continuous classes, 5th Australian Joint Conference on Artificial Intelligence. Singapore: 343–348. |
| Sattari M T, Pal M, Apaydin H, et al. 2013, M5 model tree application in Daily River flow forecasting in Sohu Stream, Turkey. Water Resources, 40(3): 233–242. DOI:10.1134/S0097807813030123. |
| Wang H B, Sassa K, Xu W Y. 2007, Analysis of a spatial distribution of landslides triggered by the 2004 Chuetsu earthquakes of Niigata Prefecture, Japan. Natural Hazards, 41(1): 43–60. DOI:10.1007/s11069-006-9009-x. |
| Wang Y, Written I H, 1997, Induction of model trees for predicting continuous classes, Poster papers of the 9th European Conference on Machine Learning. |
 2017, Vol. 33
2017, Vol. 33



