2. 中国地震局地震研究所, 武汉 43007;
3. 中国地震局地球物理研究所, 北京 100081;
4. 中国地震局地壳应力研究所, 北京 100085
2. Institute of Seismology, CEA, Wuhan 430071, China;
3. Institute of Geophysics, CEA, Beijing 100081, China;
4. Institute of Crustal Dynamics, CEA, Beijing 100085, China
“十五”数字地震观测网络项目完成后,地震前兆台网已发展成为以数字化观测为主、人工及模拟观测为辅的大台网。数字化观测手段包括水位、水温、气氡、气汞、氦气、地倾斜、地应变、重力、地磁、地电阻率、地电场等十几种,采样间隔为秒、分钟或小时。目前,基于地震行业网络的前兆台网技术系统已建成,通过该系统,数字化观测数据每天准实时从台站、区域中心自动汇集到国家前兆台网中心前兆数据库,数据量达1.1 GB/天。
前兆观测技术系统的自动化、网络化要求台网管理工作自动化、高效化,还要求各区域前兆台网中心、各学科台网中心和国家台网中心的台网管理人员快速掌握台网数据的质量状况,以便及时捕捉台网运行问题并作出快速反应,快速根据质量的优劣对观测数据进行分级服务。
目前,了解数据质量情况的唯一渠道是各学科每月、每年开展的观测资料质量评比工作。尽管各学科的每个测项各自都有一套完整的评价指标,但直接采用该评价体系存在3个方面的问题:
(1) 学科评比标准中的评比对象为具体的某个台站的某个测项,缺少包括多学科、多测项的台网综合质量评价方法。
(2) 评比时间较长,无法实现快速评价,即现有评价指标包括定量、半定量和定性等3种指标,其中,半定量、定性指标占比较大,完成1个中等大小的台网(如有70套左右观测仪器的湖北台网)的月评比至少需要3天,年评比时间则更长。
(3) 学科评比的结果是对数据质量(包括观测数据的连续性和有效性、噪声水平、观测精度、动态波形等)、运行维护、数据预处理与分析、产出应用等4个方面的综合反映,不同学科的数据质量分值占测项评比总分的比例差异较大,如年评比中水位数据质量分值所占比例为75%,而地电阻率数据质量分值则占60%。
为了能对整个前兆台网的数据质量进行快速而科学的评价,需要研究1套新的评价指标和台网数据质量评价方法。该方法的评价对象限定为观测数据,评价指标从各学科已有的、成熟的数据质量指标(表 1)中选取,对于定量化程度较低的运行维护、数据预处理与分析、产出应用等方面的指标,其优劣最终都会不同程度地体现在数据质量上,故不再作为指标引入。在对前兆台网数据质量进行评价时须均衡考虑各学科、各测项数据质量分值所占的比例。
| 表 1 现有学科评比办法中数字化测项数据质量指标 |
对于服务于地震预测的前兆台网而言,数据质量优秀的基本标准是观测数据能真实反映观测量,动态变化背景清晰,具有记录到地震、构造活动或其他地球物理事件的能力。因此要求数据质量指标应能满足观测数据的连续性或完整性、动态稳定与噪声水平、观测精度等方面的评价需求,此外,为了实现快速评价,最好能够根据前兆数据库已存储信息快速自动计算。
收集地下流体、形变、电磁学科的观测资料评比办法①,从中提取数字化观测项目(水位、水温、气氡、气汞、氦气、摆式倾斜(包括水平摆、垂直摆和钻孔倾斜等)、水管倾斜、洞体应变、体应变、分量应变、重力、地磁、地电阻率、地电场等共计14种观测手段)的所有数据质量指标(表 1)。
①中国地震局监测预报司, 2015, 地壳形变学科、电磁学科、地下流体学科观测资料质量评比办法
通过对表 1质量指标的评价内容及其计算方法进行分析,对以下情形进行了处理:
(1) 对部分指标进行了取舍
水位动态变化特征指标中标准差与水位M2波观测精度之间存在矛盾,水位M2观测精度反映了水位潮汐与体应变理论固体潮的相对误差,基本能评价水位动态变化的噪声水平,故不再采用标准差这一动态变化特征指标。地电阻率、地电场的连续率与完整率指标均是对数据连续性的评价,完整率是有效数据占应产出数据的比例,反映有效数据的连续性;而连续率则是仪器产出数据占应产出数据的比例,反映观测系统产出数据的能力,从数据应用的角度及现有观测技术水平来看,完整率更实用,故舍弃连续率指标。
(2) 对实质相同而命名不同的指标进行了名称统一
潮汐因子相对中误差:在水位评比办法中称为观测精度,规范名称为潮汐因子相对中误差。
潮汐因子中误差:在重力评价办法中称为调和分析精度,在形变评比办法中称为潮汐因子均方误差,统一规范名称为潮汐因子中误差。
(3) 对一些指标笼统的名称规范为与评价方法相关的名称
水温的动态变化特征指标规范命名为标准差,而气氡、气汞的动态变化特征指标规范命名为相对标准差;水温、气氡、气汞等的内在质量指标均重新命名为超差数。
倾斜的相对噪声水平即变形监测数据常用的质量检验方法——均方连差(岳建平等,2010)规范为均方连差;地电阻率观测精度规范为月相对标准差。
经过筛选与规范,共有14个数据质量指标成为前兆台网数字化测项的数据质量评价指标,指标分值仍采用学科评比办法中的相应指标分值(表 2)。
| 表 2 用于台网数字化观测数据质量评价的指标及其分值 |
根据评价内容、方法的不同,这14个指标又可分为数据完整性、噪声水平、固体潮汐参数、一致性检验指标等4类。
1.1 数据完整性指标数据完整性指标是数据质量评价最为基础的一项指标。完整率为仪器产出的有用数据总数与仪器应产出的数据总数之比,反映仪器运行状态及产出数据的可用情况。有用数据可被认为是原始观测数据按照各学科预处理标准预处理后的非空预处理数据。
1.2 噪声水平指标噪声水平指标与观测环境、观测系统噪声水平等直接关联,主要反映数据动态变化的稳定性水平。这类指标的计算主要基于统计学的均值、标准差等方法,包括了地下流体学科常用的标准差、相对标准差、超差数,地电采用的月相对标准差,形变采用的均方连差和地磁的背景噪声等指标。
1.2.1 地下流体的标准差、相对标准差和超差数标准差、相对标准差、超差数等被地下流体学科用来评价观测数据的噪声水平和内在质量水平。相对标准差与标准差均是通过数据的离散度来评价噪声水平的,其值越小,动态变化越稳定,两者不同的是相对标准差消除了观测值大小对标准差的影响,适用于动态变化起伏较大的化学量如气氡、气汞观测数据的噪声水平评价(中国地震局监测预报司,2002b)。
假定观测数据序列为{xi,i=1,2,3…n},序列的均值为u。首先对观测数据序列进行消除趋势处理,考虑到地下流体测项动态变化的复杂性,一般采用移动平均法消除趋势(周克昌等,2011)。消除趋势后的数据序列为{yi,i=1,2,3…n},其均值为v,则标准差σ、相对标准差δ的计算方法为
| $ \sigma {\rm{ = }}\sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {\left({v - {y_i}} \right)} } \;\;\;\delta = \frac{\sigma }{u} $ | (1) |
超差数为超过k倍标准差的超差次数,一般k为3。超差数越大,数据突变(突跳、台阶)越多,噪声水平越差。满足超差的条件为
| $ {y_i} - v > k\sigma \;或\;{y_i} - v < - k\sigma $ | (2) |
相对标准差用来评价地电阻率观测的噪声水平。每天每个测道的小时相对标准差的日平均值为日相对标准差,每月所有测道日相对标准差的平均值为月相对标准差kσn,计算公式为
| $ {k_{{\sigma _n}}} = \frac{1}{N}\left\{ {\sum\limits_{i = 1}^n {\left[ {\frac{1}{D}\sum\limits_{i = 1}^n {\left({\frac{1}{H}\sum\limits_{i = 1}^n {\frac{{{{\left({{\sigma _n}} \right)}_{kji}}}}{{{{\left({{\rho _{\rm{s}}}} \right)}_{kji}}}}} } \right)} } \right]} } \right\} $ | (3) |
其中,N为台站的测道数;D为当月的天数;H为1天中小时观测数据的个数;(σn)kji为当月第j测道第i天第k小时地电阻率测值的均方差;(ρs)kji为当月第j测道第i天第k小时地电阻率测值。
1.2.3 倾斜应变的均方连差利用日均值消除潮汐变化后的均方连差法来评价倾斜、洞体应变等测项的观测数据非潮汐部分的噪声水平(中国地震局监测预报司,2002a)。与流体的标准差类似,均方连差越小,表示测项观测数据的非潮汐部分噪声水平越低。假定观测数据日均值序列{yi}的均方连差为q2,计算公式为
| $ {q^2} = \frac{1}{{N - 1}}\sum\limits_{i = 1}^{N - 1} {{{\left({{y_{i + 1}} - {y_i}} \right)}^2}} $ | (4) |
其中,N为计算天数(≥90(即3个月))。
1.2.4 地磁的背景噪声背景噪声主要用来评价地磁相对观测各要素(F、Z、H、D)的噪声水平。若背景噪声值处于较低水平,则说明观测质量较好(中国地震局监测预报司,2002c;闫计明等,2013)。以月尺度的背景噪声计算为例,具体算法如下①:
从地磁台网的东、南、西、北、中各选择1个台站,计算这5个台站H分量当月3hr时段的一阶差分的标准差,从中选择相对于这5个台站标准差均最小的5组3hr时段,认为它们是该月该台网噪声最小的时段,将其作为该月背景噪声计算时段。
某台站要素k第j组3hr时段内,统计该要素的一阶差分绝对值频次从大到小的序列为{Cikj},对应的一阶差分绝对值序列为{Yikj},要素k在第j组3hr时段的噪声Skj计算公式为
| $ {S_{kj}} = \frac{{2 \times \sum\limits_{i = 1}^m {\left({{Y_{ikj}} \times {C_{ikj}}} \right)} }}{{\sum\limits_{i = 1}^m {{C_{ikj}}} }}\;\;\;\;\;\;\;\sum\nolimits_{i = 1}^m {{C_{ikj}} \ge 80\% } $ | (5) |
其中,i=1,2,…,m,m为Cikj依次累计超过80%的最小累计数;k为F、Z、H、D要素;j={1,2,3,4,5}。
根据式(5) 计算得到要素k的5个噪声值,剔除最大值,求平均,即为要素k的月噪声值。
1.3 固体潮汐参数指标固体潮汐参数指标主要用来评价能够观测到固体潮汐变化的重力、地倾斜、地应变、地下水位等测项的内在观测质量,其包括Nakai检验百分比、M2潮汐因子、M2潮汐因子中误差和M2波潮汐因子相对中误差等4个指标。之所以选择固体潮汐中的半日波——M2波参与评价,主要是考虑到中国地震监测台网绝大多数都分布在中纬度地区,而中纬度地区的M2波振幅最大,具有最大的信噪比(陈华静,2002)。
(1) Nakai检验百分比。该指标主要用于重力学科评价观测序列固体潮记录的总体情况,其值为观测时间序列中与理论固体潮相关性较高、噪声水平较小的观测数据段所占的比例。对观测数据序列按2天分组,对每组数据进行Nakai检验(中国地震局监测预报司,2002a),统计中误差小于2微伽的组数占总组数的比例。
(2) M2潮汐因子。该指标主要是地下流体中的水位测项用来评价其固体潮响应幅度的大小,其值为观测的固体潮M2波振幅与理论固体潮M2波振幅的比值。该值越大,且M2潮汐因子中误差越小,则内在质量越好。该指标采用Venedikov调和分析方法计算得到(周克昌等,2011)。
(3) M2潮汐因子中误差。该指标主要用于重力、地倾斜以评价固体潮观测精度,其值为Venedikov调和分析中每2天1组计算出的观测固体潮M2振幅与M2理论值振幅之比值序列的标准差。该值越小,观测精度越好。
(4) M2潮汐因子相对中误差。该指标主要用于水位、洞体应变和钻孔应变等,以评价固体潮观测精度,其值为M2潮汐因子与M2潮汐因子中误差的比值。该指标与M2潮汐因子中误差的不同在于,后者消除了潮汐因子值的大小对观测精度指标的影响。
(5) M2潮汐因子均方差。该指标用于地倾斜,以评价固体潮M2潮汐因子序列的离散程度,也可称为M2潮汐因子序列的标准差。
1.4 一致性检验指标 1.4.1 四分量应变自检内精度根据四分量应变的校正系数来检验观测数据的可靠性。设si为观测数据,Si为实地标定后的结果,{Si=kisi,i=1,2,3,4},ki为各分量的相对校正系数。当探头与围岩的耦合处于理想状态时,ki=1。根据任意2个互相正交方向的测值之和均相等的自检条件,则有
| $ {S_1} + {S_3} = {S_2} + {S_4}\;\;\;\;\;即\;{k_1}{s_1} + {k_3}{s_3} = {{\rm{k}}_2}{{\rm{s}}_2} + {{\rm{k}}_4}{{\rm{s}}_4} $ | (6) |
给定k1=1,将大量观测数据代入式(6),可计算得到k2、k3、k3;依次给定ki为1,计算其他分量的标定系数,可得到4组ki(i=1,2,3,4)。对4组ki取平均值作为最终的标定系数。ki越接近1,且各相对校正系数偏差越小,则越反映出探头与围岩耦合较好,仪器格值一致可靠(中国地震局监测预报司,2002a;邱泽华等,2005;唐磊等,2010;刘琦等,2011)。
1.4.2 地电场相关系数采用地电场侧向的长、短极距相关系数检验观测数据的可靠性(中国地震局监测预报司,2002c)。若地电场相关系数>0.95,则认为观测质量较好。地电场月相关系数R月计算方法如下:
首先,利用该侧向的长、短极距每小时测得的分钟值数据计算长极距、短极距测值间的相关系数R时
| $ {R_{时}} = \frac{{\sum\nolimits_{i = 1}^n {\left({{E_{{短_i}}} - \overline {{E_短}} } \right)\left({{E_{{长_i}}} - \overline {{E_长}} } \right)} }}{{\sqrt {\sum\nolimits_{i = 1}^n {{{\left({{E_{{短_i}}} - \overline {{E_短}} } \right)}^2}{{\left({{E_{{长_i}}} - \overline {{E_长}} } \right)}^2}} } }} $ | (7) |
式中,E长i为某长极距测道第i个地电场的分钟观测数据;E长为该测道观测数据的平均值;E短i为短极距测道的第i个地电场的分钟观测数据;E短为该测道观测数据的平均值;n为计算的每小时分钟值观测数据的个数。
然后,计算每天R时的均值、标准差,根据3倍标准差准则,剔除超出3倍均差的值后再计算平均值作为日相关系数R日。各测向日相关系数的平均值即为地电场月相关系数R月
| $ {R_月} = \frac{1}{n}\sum\limits_{j = 1}^n {\frac{1}{m}} \sum\limits_{j = 1}^n {{R_{日ij}}} $ | (8) |
式中,n为当月天数;R日ij为第i个测向第j天的相关系数;m为侧向数。
1.4.3 地电场差值用差值判断地电场同一测向观测数据的变化幅度是否一致,是否存在漂移现象。差值的计算方法为:首先,计算同一方向不同极距或平行方向一段时间内2个测道数据的差值Dxy①,多测向的平均值即为该观测场地电场的差值。若差值小于1mV/km,则观测质量较好。
| $ {D_{xy}} = \frac{{\sum\limits_{i = 1}^n {\left| {\left({{X_i} - {X_0}} \right) - \left({{Y_i} - {Y_0}} \right)} \right|} }}{n} $ | (9) |
其中,Xi,Yi分别为2个测道的观测值;X0,Y0分别为2个测道的午夜平均值;n为时间段内数据个数。
2 台网质量评价方法采用上述数据质量指标,参照学科相应指标的评分标准(表 2),即可计算某台站某测项的数据质量得分。台网质量评价的基本思路为:首先将台网中数据质量满分各不相同的所有台站所有测项的得分进行规范化处理,然后采用多测项、多学科加权平均方法来评价某个区域台网、某个学科台网或全国台网整体的数据质量。以区域前兆台网质量评价为例,具体方法如下:
(1) 计算参与评价的所有台站所有测项的数据质量指标及其得分。设台站i测项j的数据质量指标为α1、α2、α3…αm,根据学科评比办法的评分标准计算指标得分β1、β2、β3…βm,指标得分之和即为该台站该测项的数据质量得分Sji。
(2) 采用最大-最小值规范化方法对所有台站的数据质量得分进行处理(李爱国等,2012)。假若所有测项的数据质量分的规范值为γmin、γmax,某测项j的质量得分最小值、最大值为Sjmin、Sjmax,则某台站i某测项j的数据质量分Sji的规范化值Gji可表示为
| $ {G_{ij}} = {\gamma _{\max }} - \left[ {\left({{S_{j\max }} - {S_{ji}}} \right)\left({{\gamma _{\max }} - {\gamma _{\min }}} \right)/\left({{S_{j\max }} - {S_{j\min }}} \right)} \right] $ | (10) |
(3) 计算台网中每个测项数据质量规范化结果的平均值,将其作为台网该测项的数据质量得分。假设台网中第j测项共计有n个台站,则第j测项的质量得分Tj可表示为
| $ {T_j} = \frac{1}{n}\sum\limits_{i = 1}^{i = n} {{G_{ji}}} $ | (11) |
(4) 按照地下流体(包括水位、水温、气氡、气汞和氦气等)、形变(包括摆式倾斜、水管倾斜、洞体应变、体应变、分量应变和重力等)、电磁(包括地磁、地电阻率和地电场等)等3个学科,分别计算台网的学科得分δi(i=1,2,3)。假设台网中共计有m类流体测项(C1,C2,C3,…Cm),每类测项对应的台站数量分别为D1、D2、D3、…Dm,则流体学科的得分δ1为
| $ {\delta _1} = \frac{1}{{\sum\limits_{k = 1}^m {{D_k}} }}\sum\limits_{i = 1}^{i = m} {{D_i}{T_{{C_i}}}} $ | (12) |
(5) 根据学科的得分,计算台网数据质量得分ξ。假定台网的流体、形变、电磁等台站的数量分别为B1、B2、B3,台网的流体、形变、电磁等学科的质量得分分别为δ1、δ2、δ3,则
| $ \xi = \left({{B_1}{\delta _1} + {B_2}{\delta _2} + {B_3}{\delta _3}} \right)/\left({{B_1} + {B_2} + {B_3}} \right) $ | (13) |
采用上述方法,对2013年我国30个区域台网(共计1428套数字化仪器)进行了评价。
3.1 观测数据初步审核首先,对30个台网2013年全年的数字化观测数据的预处理数据进行审核,对审核时发现的预处理数据中的错误数据、故障数据等问题数据再次进行剔除、改正等预处理,以保证参与评价的数据均为可用的观测数据。
3.2 数据质量指标计算利用前兆数据质量评价软件,计算参加评价的所有测项的数据质量指标及其得分。对计算结果采用动态曲线法进行复核。复核结果显示,对于有着明显的检验参照物的测项,采用与参照物相关的质量指标(如倾斜、形变、重力、水位的固体潮参数等)来进行质量评价,评价结果基本准确,而对于气氡、气汞和地电场等其它测项,评价结果的正确率为90%~95%。以气氡为例,共计84个观测站的气氡测项参与评价,其中8个质量评价为优的观测站,实际上由于观测装置设计的缺陷或受干扰因素的影响,质量应为中或差,除此之外,评价结果均准确,正确率为90.5%。
经过复核改正后,数字化测项中重力测项优秀率最高,为100%,其次为地磁、水管倾斜、洞体应变和水温等测项,优秀率较低的测项为地电场和气汞(图 1)。全国前兆台网质量优秀率为80.7%,与各学科质量监控结果基本一致。其中,地电场测项因环境干扰较普遍,故优秀率较低;气汞测项则由于仪器老化、故障率较高而观测质量较差。
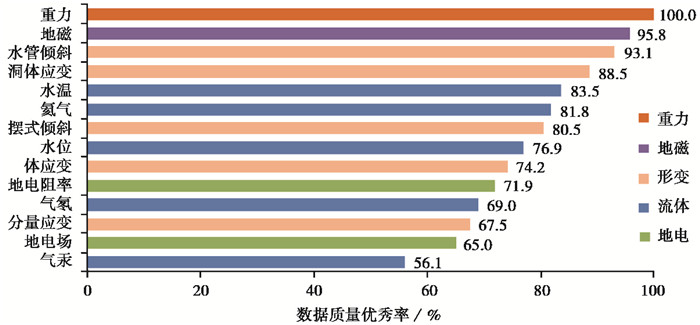
|
图 1 2013年各数字化测项数据质量优秀率 |
在分值规范化时,测项质量得分的最大值、最小值取自该测项全国所有台站而不是某个区域台网的台站。考虑到各测项质量评价结果的最大值一般为满分,而最小值之间却存在明显差异。为了缩小差异,通常将所有测项的质量得分规范至(50,100),根据各学科仪器占台网的比例进行加权平均,计算得到各区域台网数据质量得分,结果如图 2曲线a所示。这种对质量得分的处理方法与简单地按照100分折算的方法(图 2曲线b)相比,各台网的评价结果相差不大。评价结果显示,30个区域台网数据质量得分均大于85分,其中,83%的区域台网质量得分不小于90分。
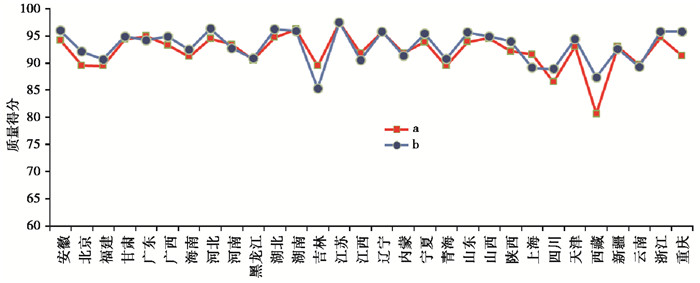
|
图 2 2013年各区域地震前兆台网数据质量评价结果 |
此外,在实际评比中,为了各学科的均衡发展,在计算得到各区域台网各学科的得分后,综合台网质量得分时采用了“三分天下”的计算方法,即地下流体、形变、地磁等3大学科的得分权重均为1/3。经过这些处理后,评价的得分值只能作为参考,而排名则更具实际意义,它反映了该区域台网整体的观测数据质量水平在全国所处的位置。
4 结语本文在现有学科评比办法的基础上,研究获得了一套相对较完整的前兆台网数字化测项数据质量评价方法。利用该方法对2013年我国区域前兆台网数字化数据质量进行了快速评价。评价结果显示,测项的质量评价正确率大于90%。数据质量指标得分经复核后,对台网的评价结果基本能反映台网的数据质量实际状况。该方法已应用在全国区域前兆台网质量评比工作中,为实现我国前兆台网数据质量的快速评估、质量分级分类打下了基础。
前兆台网数字化测项观测质量评价方法是近年来随着数字化观测技术的发展而提出的新研究课题。目前的研究还处于起步阶段,尚存在一些问题,如某些测项评价指标不全、测项之间同类指标评分差异较大;普遍缺少环境干扰、背景动态等评价指标,在完成了自动计算后,还需要结合动态波形来复核结果以保证结果的正确性等。今后还需要通过重新评估现有的学科数据质量指标,统一各测项各类指标的评分标准,增加反映环境干扰程度、背景动态等的量化指标,才有可能建立一套完备的、相对科学的台网质量评价方法。
致谢: 感谢刘耀炜研究员、杜学彬研究员、陈志遥研究员、杨冬梅研究员等在数据质量评价方法研究过程中提供的帮助,感谢评审专家在完善论文方面提出的意见和建议。| 陈华静. 2002, 京津翼晋地区水位潮汐响应函数动态特征研究. 地震, 22(4): 9–16. |
| 李爱国, 库向阳. 2012, 数据挖掘原理、算法及应用. 西安: 西安电子科技大学出版社. |
| 刘琦, 张晶, 池顺良. 2011, 四分量钻孔应变资料的质量评价及拟合分析. 地震, 31(2): 87–96. |
| 邱泽华, 石耀霖, 欧阳祖熙. 2005, 四分量钻孔应变观测的实地绝对标定. 地震, 25(3): 27–34. |
| 闫计明, 张亮娥, 陈常俊, 等. 2013, 太原基准地震台地磁背景噪声分析. 地震地磁观测与研究, 34(5/6): 135–139. |
| 岳建平, 田林亚. 2010, 变形监测技术与应用. 北京: 国防工业出版社. |
| 中国地震局监测预报司. 2002a, 地壳形变数字观测技术. 北京: 地震出版社. |
| 中国地震局监测预报司. 2002b, 地下流体数字化观测技术. 北京: 地震出版社. |
| 中国地震局监测预报司. 2002c, 电磁数字化观测技术. 北京: 地震出版社. |
| 周克昌, 等. 2011, 前兆台网数据处理与评价方法理论模型. 北京: 地震出版社. |
 2017, Vol. 33
2017, Vol. 33


