2. 山东省地震局, 济南 250014
2. Earthquake Administration of Shandong Province, Beijing 250014, China
地震地电阻率前兆观测在国内外已受到众多地震学家的广泛关注,从20世纪50年代开始,日本、前苏联、美国、中国等相继开展了地震地电阻率实验观测,陆续报道了与地震相关的异常以及理论和承载实验等方面的研究(Brace et al,1968;Borsukov et al,1973;Mazzella et al,1974;Yamazaki,1975;Wang et al,1975)。其中,我国地电阻率观测在大震前记录到了显著的中短期异常,异常多以趋势性下降变化、破年变为主,且在震级7级以上的震例中具有明显的可重复性(钱复业等,1980、1982;桂燮泰等,1989;钱家栋等,1998;Lu et al,1999;赵玉林等,2001;张学民等,2009;杜学彬,2010)。目前,我国大陆主要地震断裂带上80多个定点观测地电台承担着常规的地震监测任务,其中部分台站已连续观测40多年,并对台网内的一些中强地震进行了1年时间尺度的中短期预测(叶青等,2005;杜学彬等,2013)。
地震地电阻率观测多采用对称四极装置,布设2~3个测道,供电电极、测量电极埋深一般为1.5~2.0m,供电极距约为1200m,地下的探测深度或探测范围为数百米(杜学彬等,2008;钱家栋等,1985)。随着城市化进程、工农业生产和交通运输电气化的发展,地表大极距的地电阻率观测环境趋于恶化。地电阻率观测的干扰源主要包括地表潜水位的升降变化、测区地表游散电流(工农业用电漏电、直流运输系统干扰等)、测区内局部异常体(金属管网、挖土水坑等)等(李菊珍等,2004;何康等,2010;陈远东等,2010;刘允秀等,1999;张学民等,1996;张国苓等,2013、2015)。解滔等(2012、2013)、石富强等(2014)从数值分析方面计算了金属管网类干扰对地电阻率观测的影响。本文则主要研究地表直流点电流对地电阻率观测的影响,使用供电、测量电极位于地表的大极距对称四极观测装置,将干扰点电流源置于地表的相对于观测装置中心点O的不同位置,计算干扰点电流增减及位置变化等对地电阻率的影响。
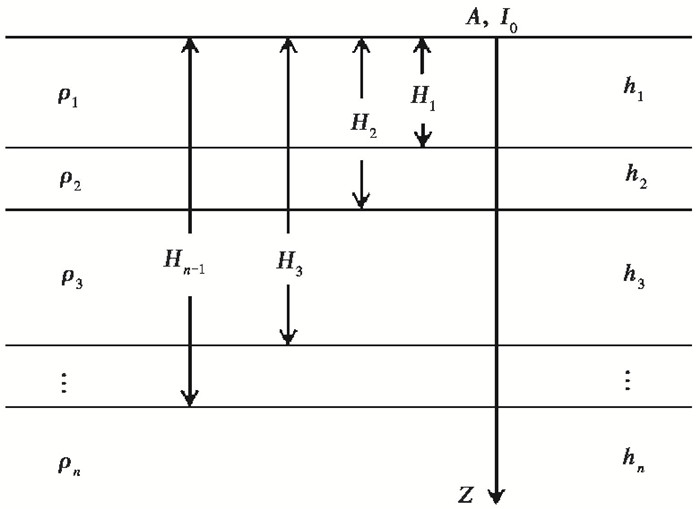
1 计算方法地电阻率台站地下介质可简化为水平层状介质模型(图 1),模型由n层水平分层介质组成。第n层厚度为无穷大,其余各层厚度h1,h2,…,hn-1等均有限。Hi表示第i层介质下界面埋深。各层介质在电学性质上都是均匀的、各向同性的。地层中的电场由位于地表A处的一点电流源产生,该点电流源向地下供直流电,电流强度为I0。电位V相对于通过点源A与地面垂直的轴线呈圆柱状分布。若取柱坐标系,A为坐标原点,Z轴垂直向下,l为测点到Z轴的水平距离,其沿地表平行于表层;z为地层的厚度,则稳定电流场的电位满足拉普拉斯方程
|
图 1 水平层状大地模型 |
| $ \frac{{{\partial ^2}V}}{{\partial {l^2}}} + \frac{1}{l} \cdot \frac{{\partial V}}{{\partial l}} + \frac{{{\partial ^2}V}}{{\partial {z^2}}} = 0 $ | (1) |
当水平层状大地点电流源的稳定电流场满足以下边界条件(姚文斌,1989):地下各层分界面处电位连续,即z=Hi时,Vi=Vi+1;地下各层分界面处电流密度法向分量连续,即
| $ \frac{1}{{{\rho _i}}} \cdot \frac{{\partial {V_i}}}{{\partial z}} = \frac{1}{{{\rho _{i + 1}}}} \cdot \frac{{\partial {V_{i + 1}}}}{{\partial z}} $ | (2) |
式中,ρi为第i层介质电阻率值。此时,地表除了电源的无穷小领域外,其他电流密度法向分量均等于0,即
| $ \frac{1}{{{\rho _i}}} \cdot \frac{{\partial {V_1}}}{{\partial z}} = 0\;\;z = 0 $ | (3) |
在电流源附近,当
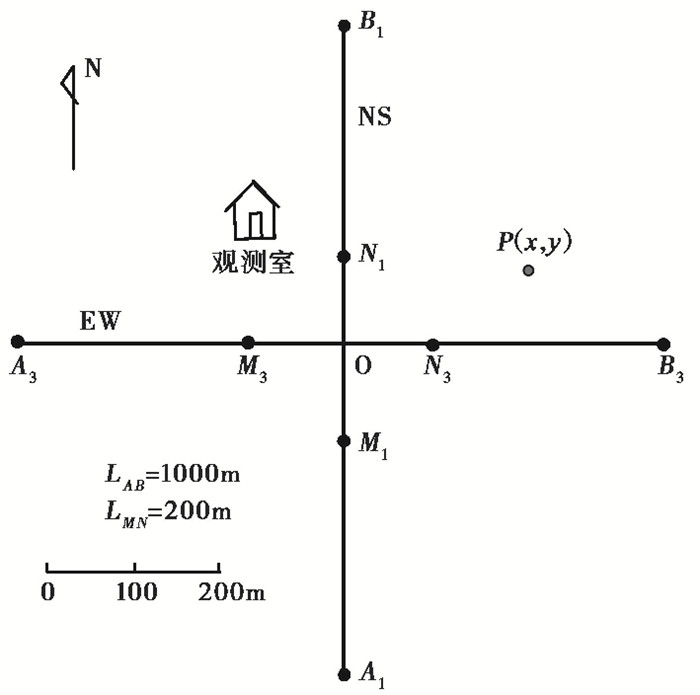
地电阻率观测采用的对称四极观测装置如图 2所示,A、B为供电电极,M、N为测量电极,电极均位于地表以下1.5~2.0m,采用EW、NS两个垂直测向布极,中心点为O。测量电极M、N之间的电位差ΔUMN=UAM-UAN-UBM+UBN,装置系数K=π(r2-b2)/2b,其中,r=LAB/2,b=LMN/2,规定c=b/r为装置的偏心率。选择对称四极装置的奥尼尔滤波器,利用转换函数滤波器法计算地电阻率ρa(O'Neill et al,1984),视电阻率函数表达式为
|
图 2 地电阻率布极 |
| $ {\rho _{\rm{a}}} = 2r\left({1 - {c^2}} \right)\left({4c} \right)\int_0^\infty {T\left(\lambda \right)\left\{ {{J_0}\left[ {\lambda r\left({1 - c} \right)} \right] - {J_0}\left[ {\lambda r\left({1 + c} \right)} \right]} \right\}{\rm{d}}\lambda } $ | (4) |
式中,λ为积分变量,具有长度倒数量纲;J0为第1类零阶贝塞尔函数;T(λ)=ρ1[1+2A1(λ)]为电阻率转换函数;A1(λ)为核函数。T(λ)、A1(λ)仅与地下各层的电阻率、厚度等有关,与电极距r无关,是表征地电断面性质的函数(姚文斌,1989)。
依据地电阻率实际测量的电流I、地电阻率ρa、对称四极装置系数K,得到MN之间的电压为
| $ \Delta {U_{MN}} = {\rho _{\rm{a}}} \cdot I/K $ | (5) |
当测区P点有干扰电流I′从地表输入时,会在M、N间产生附件电位差ΔU′ MN并叠加在供电电位差ΔUMN上。P点干扰电流在M、N点产生的干扰电位差可看作二极观测装置,P点为供电电极,M、N点分别为测量电极。装置系数KPM=2πLPM,KPN=2πLPN,其中,LPM、LPN为P点到M、N点的距离。选择理论二极装置的奥尼尔滤波器,利用转换函数滤波器法计算M、N点的地电阻率ρPM、ρPN,计算公式为
| $ \begin{array}{l} {\rho _{PM}} = {L_{PM}}\int_0^\infty {T\left(\lambda \right){J_0}\left(\lambda \right){\rm{d}}\lambda } \\ {\rho _{PN}} = {L_{PN}}\int_0^\infty {T\left(\lambda \right){J_0}\left(\lambda \right){\rm{d}}\lambda } \end{array} $ | (6) |
P点干扰电流I′在M、N点产生的干扰电压按下式计算
| $ \begin{array}{l} {U_{PM}} = {\rho _{PM}} \cdot I'/{K_{PM}}\\ {U_{PN}} = {\rho _{PN}} \cdot I'/{K_{PN}} \end{array} $ | (7) |
干扰电流I′在对称四极观测装置系统上产生的附加地电阻率为
| $ {\rho _{\rm{d}}} = K \cdot \frac{{{U_{PM}} - {U_{PN}}}}{I} $ | (8) |
将附加地电阻率ρd与地电阻率观测值ρa的比值ε作为干扰电流I′的影响,表示为
| $ \varepsilon = {\rho _{\rm{d}}}/{\rho _{\rm{a}}} $ | (9) |
本文以4层水平层状一维KH型均匀介质为例予以讨论,电性结构参数为ρ1=40Ω·m,H1=10m;ρ2=80Ω·m,H2=40m;ρ3=30Ω·m,H3=80m;ρ4=40Ω·m,H4=αm。地电阻率采用对称四极观测装置,供电极距为2000m,测量极距为500m,供电电流为2A。点电流位于地表(H=0) 处,垂直向下供电,计算该点电流EW向的ε值。
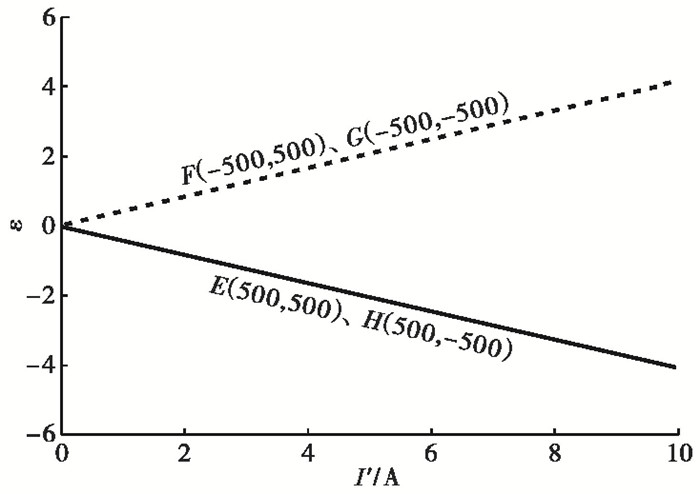
2.1 点电流对地电阻率观测值的影响将测区中干扰点电流依次置于测区的E(500,500)、F(-500,500)、G(-500,-500)、H(500,-500) 等4点,分别计算点电流为0~10A时对地电阻率观测的影响。结果表明,地电阻率所受影响与电流强度呈线性相关(图 3)。图 3中虚线为第2、3象限内F、G点地电阻率影响量ε随电流的变化曲线,表明在OA段地电阻率影响量ε与点电流强度线性正相关;实线为第1、4象限内E、H点地电阻率影响量ε随电流的变化曲线,表明在OB段地电阻率影响量ε与点电流强度线性负相关。在测区中干扰电流位置固定时,地电阻率影响量ε随电流的增加而增大。
|
图 3 地电阻率影响量ε随电流的变化 |
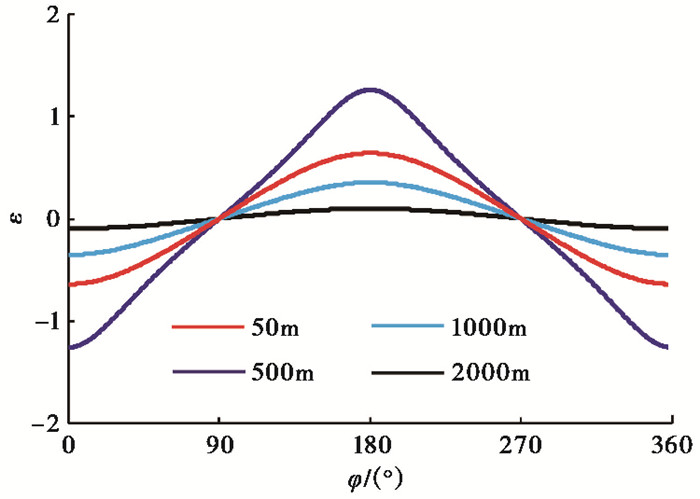
当测区中P点有干扰点电流,P点与观测装置布极中心点O的连线OP及电极连线OB之间的夹角为φ,φ值在0°~360°间逆时针变化。本文计算了干扰点电流距中心点O一定距离时随方位角φ变化而产生的EW向地电阻率影响量ε,点电流I′=1A,结果如图 4所示。由图 4可见,点电流对地电阻率的影响量ε为反余弦函数,在AB方向上,ε最大;在过中心点O且垂直于AB的方向,ε为0。
|
图 4 地电阻率影响量ε随电流方位的变化不同颜色表示干扰点电流距中心点O的不同距离 |
计算相对于O点的不同位置上干扰点电流对地电阻率的影响量ε,结果如图 5所示。由图 5可见,以过中心点O且垂直于EW测道AB的线为界,OA段为正影响,在M点及其附近影响值最大;OB段为负影响,在N点及其附近影响值最大。地表干扰电流位置与装置中心点间超过一定的距离后,影响量ε很小,在无穷远处,ε趋于0;干扰源位置接近中心线时,ε趋于0;而干扰源接近测量电极M、N时,影响量ε较大,地电阻率影响量ε可达正常观测值的数倍。

|
图 5 电流位置对地电阻率的影响 |
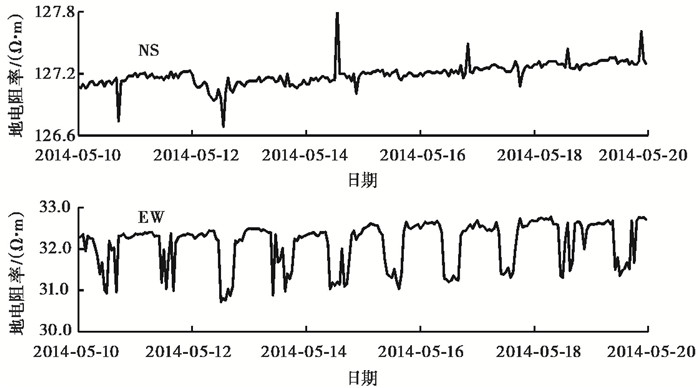
目前,地电阻率观测实际为正、反向交替供电模式,在1~2min内,先测量1次供电电流,然后正向-反向交替供电5或10次,以供电后的正向电位差减去反向电位差再取平均,即得到供电电位差,最后,利用测量电流和装置系数计算视电阻率。如果测区的干扰点电流源为固定且恒定的直流电,则上述测量方式可以消除干扰电流源的影响。但实际观测中常会出现每天固定时段、幅度略有差异的不稳定的干扰变化,例如腾冲台地电阻率2套系统的长、短极距的观测曲线变化形态基本一致,2014年5月24日之前半年内EW测道观测值每天约在8:00~17:00时段内出现阶跃性下降,长极距观测下降幅度大于短极距,而NS测道则没有同样的变化(图 6),这说明干扰电流源近乎处于EW向沿线上,且干扰电流源不稳定。通过查看腾冲台地电阻率测区发现,在EW测道东电极附近有农庄,初步认为上述现象可能是由农庄用电干扰所致。2014年7月14日中国地震台网中心调研腾冲地电阻率的变化情况①过程中也注意到,2014年春节前夕EW测道东供电极附近的村子实施农村电网改造,白天停电,其间腾冲台地电阻率每天的周期性阶跃变化消失,这进一步说明腾冲台EW测道观测值每天出现的阶跃性下降是由测道东电极附近漏电干扰引起的。
|
图 6 腾冲台地电阻率整点值变化 |
①解滔等, 2014, 2014年7月14日云南腾冲台地电阻率异常核实报告
4 讨论与结论本文利用地电阻率转换函数的递推公式定性地分析了地表点电流对地电阻率的影响,计算结果表明,地电阻率与干扰电流源的强度、位置有关。干扰点电流越大,地电阻率受到的影响越大;在测区内距中心点的距离不同,点电流对地电阻率的影响亦不同,在测线方向上的影响较大,过中心点且垂直于测线方向上的影响较小;干扰源与测区间超过一定的距离后,影响量较小,无穷远处,影响为0,在测量电极M、N点附近影响最大。
地表点电流对地电阻率的干扰具有不同测道的干扰幅度不同、同一测道干扰出现时间相似等特点,且易于识别。在实际观测异常核实过程中,可通过多测道地电阻率对点电流的不同响应判定干扰源的位置,再结合实际环境调研,则更有利于快速找到干扰源,排除其对地电阻率观测的影响。
致谢: 感谢中国地震台网中心卢军研究员、解滔以及甘肃省地震局杜学彬研究员对本项工作提供的帮助,感谢审稿专家对本文提出的宝贵意见。| 陈远东, 孙致安, 汪贵章, 等. 2010, 安徽省数字化地电阻率干扰与短临异常研究. 地震地磁观测与研究, 31(4): 86–91. |
| 杜学彬. 2010, 在地震预报中的两类视电阻率变化. 中国科学:D辑, 40(10): 1321–1330. |
| 杜学彬, 严玲琴, 范莹莹, 等. 2013, 2013年岷县漳县MS6.6地震前后地电观测引起的思考. 地震工程学报, 35(3): 513–521. |
| 杜学彬, 叶青, 马占虎, 等. 2008, 强震附近电阻率对称四极观测的探测深度. 地球物理学报, 51(6): 1943–1949. |
| 桂燮泰, 关华平, 戴经安. 1989, 唐山, 松潘地震前视电阻率短临异常图像重现性. 西北地震学报, 11(4): 71–75. |
| 何康, 王燚坤, 刘东旺, 等. 2010, 九江MS5.7地震前地电阻率异常分析. 地震地磁观测与研究, 32(3): 62–66. |
| 解滔, 杜学斌, 陈军营, 等. 2012, 井下地电阻率观测中地表电流干扰影响计算. 地球物理学进展, 27(1): 112–121. DOI:10.6038/j.issn.1004-2903.2012.01.013 |
| 解滔, 卢军, 李美, 等. 2013, 地埋钢缆对宝昌台地电阻率干扰的定量分析. 地球物理学进展, 28(2): 727–734. DOI:10.6038/pg20130221 |
| 李菊珍, 兰从欣, 鲁跃, 等. 2004, 北京数字化地电阻率干扰识别与异常分析. 防灾技术高等专科学校学报, 6(4): 9–13. |
| 刘允秀, 陈华静, 程瑞年, 等. 1999, 地电阻率与地下水位, 大气降水关系研究. 中国地震, 15(2): 91–96. |
| 钱复业, 赵玉林. 1980, 地震前地电阻率变化十例. 地震学报, 2(2): 186–197. |
| 钱复业, 赵玉林, 于谋明. 1982, 地震前地电阻率异常变化. 中国科学:B辑(9): 831–839. |
| 钱家栋, 曹爱民. 1998, 1976年唐山7.8级地震地电阻率和地下水前兆综合物理机制研究. 地震, 18(增刊): 1–9. |
| 钱家栋, 陈有发, 金安忠. 1985, 地电阻率法在地震预报中的应用. 北京: 地震出版社: 83-103. |
| 石富强, 张国强, 方炜, 等. 2014, 陕西周至地电台地电阻率年变特征分析. 地震学报, 36(6): 1113–1123. |
| 姚文斌. 1989, 电测深数值计算和解释入门. 北京: 地震出版社: 85-87. |
| 叶青, 杜学彬, 陈军营, 等. 2005, 2003年大姚和民乐-山丹地震1年尺度预测. 地震研究, 28(3): 226–230. |
| 张国苓, 乔子云, 贾立峰, 等. 2013, 隆尧地电阻率与地下水位关系分析. 地震地磁观测与研究, 34(5/6): 141–143. |
| 张国苓, 乔子云, 贾立峰, 等. 2015, 河北阳原台地电阻率变化分析. 震灾防御技术, 10(2): 464–471. DOI:10.11899/zzfy20150228 |
| 张学民, 李美, 关华平. 2009, 汶川8.0级地震前的地电阻率异常分析. 地震, 29(1): 108–115. |
| 张学民, 王志贤, 臧明珍, 等. 1996, 降雨对地电阻率干扰的分析. 华北地震科学, 14(4): 71–75. |
| 赵玉林, 卢军, 张洪魁, 等. 2001, 电测量在中国地震预报中的应用. 地震地质, 23(2): 277–285. |
| Borsukov O M, Sorokin O N. 1973, Variations in apparent resistivity of rocks in the seismically active Garm region. IzvEarth Physics, 10(1): 100–102. |
| Brace W F, Orange A S. 1968, Electrical resistivity changes in saturated rock during fracture and frictional sliding. JGeophysRes, 73(4): 1433–1445. |
| Lu J, Qian F Y, Zhao YL. 1999, Sensitivity analysis of the Schlumberger monitoring array:Application to changes of resistivity proior to the 1976 rathquake in Tangshan. China.Tectonophysics, 307(3): 397–405. |
| Mazzella A, Morrison H F. 1974, Electrical resistivity variations associated with earthquakes on the San Andreas Fault. Science, 185(4154): 855–857. DOI:10.1126/science.185.4154.855. |
| O'Neill D J, Merrick N P. 1984, A digital linear filter for resistivity sounding with a generalized electrode array. GeophysProspect, 32(1): 105–123. |
| Wang C Y, Goodman R E, Sundaram P N, et al. 1975, Electrical resistivity of granite in frictional sliding:Application to earthquake prediction. GeophysResLett, 2(12): 525–528. |
| Yamazaki Y. 1975, Precursory and coseismic resistivity changes. PureApplGeophys, 133(1): 219–227. |
 2017, Vol. 33
2017, Vol. 33


