自1960年起,地震台阵作为一种新型的地震学研究工具,已经广泛应用于不同类型波场信号的检测及地球内部不同尺度结构的成像(Birtill et al,1965;Frosch et al,1966; ;Wright,1972;Doornboos et al,1972;Kvaerna,1989;Weber et al,1996;Ritter et al,2001;Krüger et al,2001)。一个地震台阵由若干个位置接近、类型相同的地震计组成,能够保证输出波形的相干性,其记录到的信号包含了由不同慢度和方位角的波叠加而成的波场信息,相对于单台或大尺度台网观测有明显的优势(Rost et al,2002)。利用地震台阵的特点,用频率-波数分析(F-K)方法能够同时获取入射波场的慢度和方位角,因此这已发展成为一种重要的台阵数据处理手段(Brooks et al,2009;Koper et al,2010b;Picozzi et al,2010;Gal et al,2015)。
传统的F-K方法(lacoss et al,1969;Capon,1969a)最初主要用于单个频率点的窄带信号估计,Kvaerna等(1986a)提出非相干信号平均法(the incoherent averaged signal method,即IAS)并将其应用于宽频带信号的F-K分析中;Gal等(2014)通过加入对角加载因子(Diagonal Loading,即DL)对上述方法进行了改进,发现基于非相干平均法的F-K方法具有减小慢度估计误差,提高F-K谱稳定性的优势。此外,在基于台阵进行微震噪声的研究中,不同频率的背景噪声在传播过程中会产生来自不同方位角的多次波,从而增加了噪声源的检测难度(Brooks et al,2009;Koper et al,2010a;Traer et al,2012;Gal et al,2015;Gal et al,2016)。传统F-K方法的分辨率和精度有限,难以满足检测到所有弱源的需求。研究表明,台阵布局包括台阵孔径、几何形状及地震台数等是影响分辨率的重要因素(Okada,2003;Nishida et al,2008;Picozzi et al,2010)。台阵响应函数(Array Response Function,即ARF)逐渐被引入作为衡量台阵布局的定量化因子(Horike,1985;Halldorsson et al,2009)。为了减弱台阵响应函数对功率谱的模糊效应,Nishida等(2008)利用Richardson-Lucy(即RL)反卷积方法(Richardson,1972;Lucy,1974)对台阵响应函数与由最大似然法获取的F-K图像进行反卷积,提高了成像分辨率;Picozzi等(2010)利用RL和Tikhonov Regularization(即TR)(Bertero et al,1998)两种反卷积方法从F-K谱中去除了台阵响应函数,通过比较发现RL反卷积优于TR反卷积,能够有效提高分辨率;Gal等(2016)利用原本用于天文学的CLEAN-PSF方法(Sijtsma,2007),通过不断迭代压制强干扰源,从而提高了对弱噪声源的检测能力。
各种不同类型台阵的陆续建设,为F-K分析提供了大量的数据支持,使得该方法在理论和实践中都得到了极大的发展。人们对F-K方法的不断改进(Kvaerna et al,1986b;Gal et al,2014;Gal et al,2016;Picozzi et al,2010),使其应用领域也从分析地震事件拓展到研究包括噪声在内的其他多种不同类型的波场(Rost et al,2002;Rost et al,2009;Koper et al,2010b)。本文首先介绍了F-K分析方法的发展,然后就其在检测微弱信号源、分析噪声特征、提取面波频散曲线及评估台阵设计优劣等4方面的应用进行综述。
1 F-K分析方法从原理上来说,F-K方法是基于频率波数域功率谱密度函数(F-K PSDF)的计算,将台阵观测信号从时间-空间域转换到频率-波数域,从而获取入射波场能量在不同慢度和方位角的分布。根据窗函数的不同,可分为聚束法(Lacoss et al,1969)、最大似然法(Capon,1969a)和多信号分类法(Schmidt,1986)等。由于地震台阵记录到的都是多源波场信号,多信号分类法很难确定信号子空间的振源数量(师黎静,2007),在此不再介绍。聚束法和最大似然法是为了进行核爆检测而提出的,是目前最常用的两种F-K分析方法。
1.1 F-K谱Lacoss等(1969)给出了基于聚束法的F-K谱估计:
| $ E{P_b}({\rm{f,k}}) = \sum\limits_{n,m = 1}^N {{\phi _{nm}}} \exp \left[ {{\rm{i}}k\left( {{{\rm{X}}_m} - {{\rm{X}}_n}} \right)} \right] $ | (1a) |
Capon(1969a)提出了基于最大似然法的F-K谱估计:
| $ E{P_m}({\rm{f,k}}) = {[ {\sum\limits_{n,m = 1}^N {\phi _{nm}^{ - 1}} \exp \left[ {{\rm{i}}k\left( {{{\rm{X}}_n} - {{\rm{X}}_m}} \right)} \right]^{ - 1}} } $ | (1b) |
此处,f表示频率,k为波数,N是台阵中所包含的地震台站数目,φnm是第n和第m个台站记录之间的互功率谱,Xn和Xm分别为第n和第m个台站的坐标。
上述两种方法最主要的不同是窗函数。聚束法在波数k0的窗函数可表示为
| $ {W_b}(k,{k_0}) = {\rm{ }}\frac{1}{{{N^2}}}\sum\limits_{n,m = 1}^N {\exp \left\{ {i\left( {k - {k_0}} \right)\left( {{X_n} - {X_m}} \right)} \right\}} $ | (2) |
最大似然法的窗函数为
| $ {W_m}(k,{k_0}) = {\rm{ }}\left| {\sum\limits_{j = 1}^N {{A_j}(f,{k_0})} } \right|{W_b}(k,{k_0}) $ | (3) |
其中
| $ {A_j}(f,{k_0}) = \sum\limits_{n = 1}^N {{{({\phi _{jn}}\exp\{ i{k_0}({X_j} - {X_n})\} )}^{ - 1}}} {\rm{/}}\sum\limits_{j,n = 1}^N {{{({\phi _{jn}}\exp\{ i{k_0}({X_j} - {X_n})\} )}^{ - 1}}} $ | (4) |
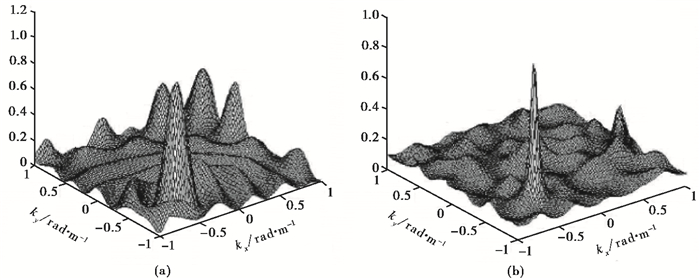
由公式(2)~(4)可以看出,聚束法的窗函数仅与台阵形状有关,相当于使用了固定的空间滤波器,最大似然法的窗函数不仅依赖于台阵形状,而且取决于数据的质量,相当于一种优化的空间滤波器,是一种非线性方法。众多研究表明,聚束法提供了频率-波数功率谱渐进无偏的一致估计,而最大似然法给出了频率-波数功率谱的最大似然估计,具有更高的分辨率(Capon,1969a;Horike,1985;师黎静,2007;吴建明,2007)。图 1给出了利用两种方法所获取的三维F-K谱示例,从中可以发现,聚束法的窗函数通常有较高的旁瓣,可能会得到虚假的F-K谱,而最大似然法的分辨率较高,所获取的F-K谱比较平滑。
|
图 1 两种F-K方法估计的三维频率-波数谱。(a)聚束法;(b)最大似然法(吴建明,2007) |
在频率f一定时,假定F-K图像的峰值出现在波数坐标(kx,ky),则此处对应的视速度为
| $ {v_{\max}} = {\rm{ }}\frac{{2\pi f}}{{\sqrt {k_x^2 + k_y^2} }} $ | (5) |
| $ {\theta _{\max}} = \tan^{ - 1}\left( {\frac{{{k_x}}}{{{k_y}}}} \right) $ | (6) |
上面提到的两种F-K方法主要应用于窄带信号的计算。从窄带拓展到宽频带有两种方法,包括相干信号平均法(the coherent averaged signal method;Wang et al,1985;Westwood,1992)和非相干信号平均法(the incoherent averaged signal method,即IAS;Wax et al,1984;Kvaerna et al,1986a;Kvaerna et al,1986b;Baggeroer et al,1993)。前者容易混淆空间位置相近的信号源,而后者对于分析具有较强频率依赖性的噪声源效果很好,能够有效提高F-K谱的稳定性。Gal等(2014)利用模拟及实际观测的噪声数据,验证了非相干平均法对于减小慢度估计误差的优势,并通过加入对角加载因子进一步提高了F-K谱的稳定性。
基于宽频带非相干平均法的最大似然F-K谱(加入了对角加载因子)是若干个离散频率点的谱总和,可表示为
| $ P\left( {f,k} \right) = \sum\limits_{j = 1}^L {[ {\sum\limits_{n,m = 1}^N {\phi _{nm}^{ - 1}\left( {f,k,\alpha } \right)\exp {{\left[ {ik\left( {{X_n} - {X_m}} \right)} \right]}^{ - 1}}} } } $ | (7) |
其中,L是离散频率点的个数,α表示DL参数。
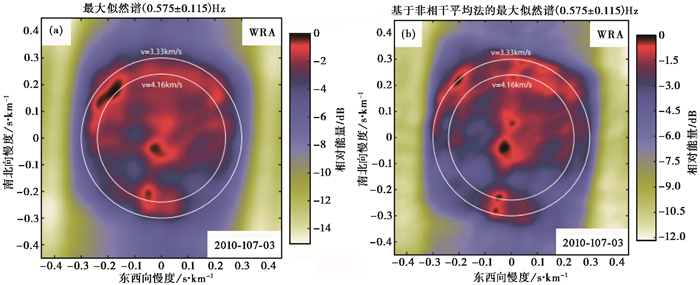
图 2给出了最大似然法和非相干平均法所获取的F-K谱,从中可以看出,尽管两种方法都能够检测到v=3.33km/s和v=4.16km/s附近的Rg和Lg震相,但也有一定的差异,相对于前者,后者能够检测到更多不同类型的源,如慢度较小的次级体波噪声源。
|
图 2 (a) 用最大似然法法获取的F-K谱;(b)基于非相干平均法获取的F-K谱(Gal et al,2014) |
在过去的数十年间,全球范围内发展了多种不同类型的台阵用于地震学的研究,如加拿大的十字形黄刀台阵(the Yellow knife Array,即YKA)、美国的大孔径台阵(the Large Aperture Seismic Array,即LASA)、德国的宽频带大孔径台阵((the Large-aperture Grafenburg Array,即GRF)、中国的上海佘山台阵等。台阵的布局是影响台阵对不同频率和慢度信号分辨能力的重要因素,可以用台阵响应函数(ARF)定量表示。对于一个给定的台阵,一些通用的准则用于衡量孔径、地震台数、台间距、台阵几何形状等因素对台阵响应函数的影响(Harjes et al,1973;Johnson et al,1992)。孔径是指台阵的最大台间距,孔径控制着F-K图像主瓣的尖锐程度,孔径越大,能够测量到的波数越小;地震台站数目决定台阵作为一个波数滤波器的分辨能力;台间距控制F-K图像的旁瓣位置,平均台间距越小,在给定波速的情况下,可识别的震相波长越小;台阵的几何形状控制入射波场的方位角分布。
台阵响应函数在波数k0处可以表示为(Horike,1985)
| $ ARF = {\rm{ }}\frac{1}{{{N^2}}}\sum\limits_{n,m = 1}^N {\exp \left\{ {i\left( {k - {k_0}} \right)\left( {{X_n} - {X_m}} \right)} \right\}} $ | (8) |
利用RL反卷积方法可以去掉台阵响应函数的影响,从而获取更高分辨率的F-K谱。
RL反卷积方法可以表示为
| $ E{\delta ^{m + 1}} = E{\delta ^m}\left( {{A^{\rm{T}}}\frac{g}{{AE{\delta ^m}}}} \right) $ | (9) |
其中,A表示台阵响应函数,m是迭代次数,g为原始的F-K谱,Eδm是经过m次迭代后的正则化解。
CLEAN算法最初用于天文学的研究,原理是通过不断迭代反卷积去掉点源(point spread function,即PSF;Högbom,1974)的影响。这种方法对于去除强源信号,提高弱源信号的信噪比具有很好的效果,逐渐被引入F-K分析中(Dougherty et al,1998;Wang et al,2004)。CELAN-PSF是一种基于CLEAN算子的改进方法,能够从互功率谱矩阵直接去除最强信号源的相位,以消除具有明显旁瓣的PSF的边界效应(Sijtsma,2007;Gal et al,2016)。
去除PSF旁瓣后的互功率谱矩阵可以表示为
| $ C_{PSF}^{i + 1} = {C^i} - \phi P_{\max }^i{w_{\max}}w_{\max }^* $ | (10) |
其中,Ф是约束因子,控制去除能量所占的比例(例如,Ф=0.05表示去除最强信号源能量的5%),wmax为每对互功率谱矩阵的权重因子矢量,wmax*是权重因子矢量的复共轭,Pmax代表功率谱中的最大值。
去除最强信号源后,重构功率谱为
| $ {P_{CLEAN}}\left( k \right) = \sum\limits_{i = 1}^M {\phi P_{\max }^i} $ | (11) |
其中,M表示迭代次数,ФPmaxi是第i次迭代时清除掉的能量。
最后得到的F-K谱为
| $ {P_{PSF}}\left( k \right) = {w}_B^*\left( k \right){C}_{PSF}^M\left( f \right){w_B}\left( k \right) + {P_{CLEAN}}\left( k \right) $ | (12) |
本文主要就F-K方法在检测微弱信号源、分析噪声特征、提取面波频散曲线、评估台阵设计优劣等4方面的应用进行综述。
2.1 检测不同类型的微弱信号源地震台阵能够在一定条件下记录到一致性较好的波形,采用F-K方法处理台阵数据,可以区分不同方向入射波场的能量分布,聚束具有相同频率、相同慢度但不同入射方向的信号,因而能够大幅度降低全球地震、核爆等不同类型事件的检测下限,这对于识别被强震掩盖的微弱事件具有良好的效果。
Li等(2016)利用ChinArray台阵数据波形识别2013年的俄罗斯陨石坠落事件时,发现由于同期汤加地震事件的干扰,很难从原始波形中分辨出相对微弱的陨石坠落信号。利用Vespagram及F-K方法对汤加地震事件的面波信号和俄罗斯陨石坠落事件进行分离,发现最终得到的震相方位角和慢度与陨石坠落事件产生的面波一致。进而应用同样的方法分析了F-net的观测记录,粗略定位了该事件的位置。说明F-K台阵处理方法对于识别较远处的微弱事件有较好的效果。
Gupta(1990)应用宽频带F-K方法,通过滑动时窗法计算了各个窗口与包括核爆P波初至在内的窗口的F-K谱残差,识别出2个不同台阵附近的近地表散射源,说明F-K方法有助于定位台阵附近的散射源。佟玉霞(2002)将同样的方法应用于上海地震台阵记录到的8个远震事件,识别出了来自相似方位和距离的短周期面波,推断是由远震P波在上海台阵南面的浙北平原与浙南山区交界区及北面的苏北盆地边缘发生散射引起的。
2.2 分析微震噪声特征现代地震仪的连续记录中,仅有一小部分是地震事件,而大多是由海洋波和自然界生物活动引起的微震噪声。众多研究表明,这些往往被视为干扰信号的噪声记录是进行地下精细结构成像,监测断裂带、火山等重要的四维地质构造,研究与海洋风暴相关的气候变化等的一种有效工具(Bromirski,1999;Grevemeyer et al,2000;Bromirski et al,2002;Shapiro,2004;Roux et al,2005;Gerstoft et al,2006;Chevrot et al,2007;Brenguier et al,2008a, 2008b;Bensen et al,2008;Stutzmann et al,2009;Aster et al,2010;Zhan et al,2010;Köhler et al,2011;Tkalĉićc et al,2012)。而噪声信号的特征对于利用其开展这些科学研究具有重要意义,F-K方法可以根据频率、慢度及传播方向分离不同的信号,是一种研究噪声源特征的有效方法。
美国LASA于1965年完成建设并投入使用,使得利用F-K方法在进行噪声特征分析上取得了一系列突破(Toksöz et al,1968;Lacoss et al,1969;Capon,1969b;Haubrich et al,1969;Cessaro et al,1989)。研究表明,1~3s只有远震体波噪声,起源于远洋风暴,与区域的活动构造关联很小;3~7s除了远震体波之外,还存在瑞雷波占主导地位的高阶面波信号;长周期7~33s只有面波信号,可分别从垂直和水平分量中识别出基阶瑞雷面波和勒夫面波,Toksöz等(1968)推断勒夫面波是由于加诸在固体介质上的剪切力或者传播路径上的地壳不规则性引起瑞雷波发生转换而产生的。同时,如果是在近海岸区域或大型湖泊附近,基阶瑞雷面波的频率会提高。其中,Cessaro等(1989)利用最大似然F-K方法,联合ALPA台阵(the Alaskan Long Period Array),不仅获取了20s的长周期噪声特征,而且采取三角测量的方法定位到了大西洋和太平洋风暴两个噪声源,利用滑动窗F-K分析方法定位到的噪声源方位角比较稳定,并不随海洋风暴位置的变化而变化,因此认为微震噪声源与远洋风暴的位置并不存在直接的关联,而是由于海洋波及其在海洋基底反射波的相互干涉引起的。
随后,越来越多不同类型台阵的建立更加丰富了F-K方法在噪声分析中的应用。Bungum等(1985)利用F-K方法分析了NORSAR(the Norwegian Seismic Array)台阵数据,提取了周期低至0.125s的信号,相速度介于3~5km/s,认为是瑞雷面波。Friedrich等(1998)分析了GRF台阵的宽频带F-K谱,发现主微震(12~20s)和次级微震(6~11s)都以基阶勒夫波和瑞雷波为主,且两个频带内勒夫波与瑞雷波之间的能量比是不同的,前者比是6 ︰ 5,后者比是1 ︰ 4。Essen等(2003)对GRF台阵4~10s的F-K分析结果显示,该频带对应于3~3.5km/s的相速度,属于基阶瑞雷面波。Gerstoft等(2006)利用聚束F-K方法研究了飓风发生时期的150个南加州台站记录,在4~6s的频带发现了相速度为11.7km/s的来自上地幔的P波。Koper等(2008)和Koper等(2009)分别在CMAR(the Chilang Mai Array)的2s附近和YKA台阵1~3s的F-K图像上,观测到了远震P波和PKP波。
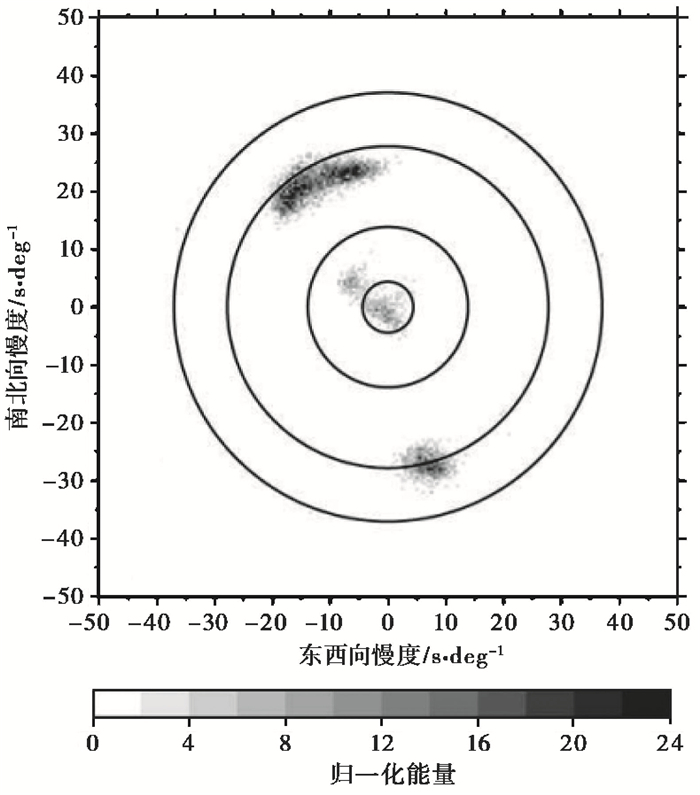
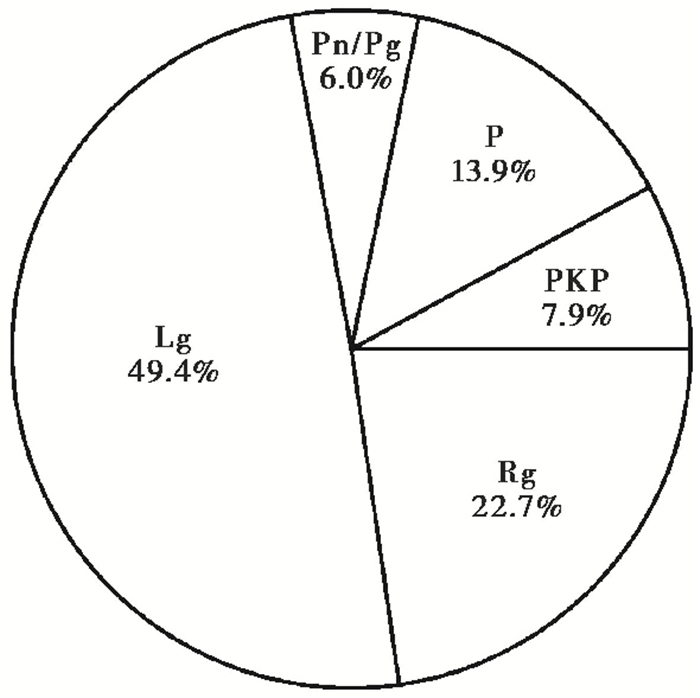
基于众多单个台阵的研究结果,Koper等(2010b)利用全球18个地震台阵连续一年的垂直向噪声记录,分析了短周期噪声(0.25~2.5 s)的构成。图 3给出了一个圆形台阵的F-K分布图。几个不同半径的圆分别对应于不同的慢度:4.4s/deg,13.9s/deg,27.8s/deg,37.1s/deg。图 4给出了利用18个台阵2007~2008年的噪声记录获得的相速度统计结果,占主导地位的是勒夫波,推断来自浅层或近海岸的海洋区域;超过25%的是各种类型的P波,包括上地幔的转换波(P,14%),近震P波(Pn/Pg,6%)和外核折射波(PKP,8%),推断其来源之一是远离海岸线的北太平洋地区,该区域是一个稳定的长期微震噪声激发源,已经激发了近40年的P波能量;基阶瑞雷面波Rg占据的比例最小,可能是由于其衰减较快,只有接收台阵距离激发源较近时方能观测到。
|
图 3 一个圆形台阵的F-K慢度分布示例图 几个不同半径的圆圈分别对应于不同的慢度:4.4s/deg,13.9s/deg,27.8s/deg,37.1s/deg(Koper et al,2010b) |
|
图 4 利用18个台阵2007~2008年的噪声记录统计获得的相速度分布(Koper et al,2010b) |
地震面波在传播过程中最重要的特点之一是存在频散现象,这一特性是由地下介质的结构和非弹性决定的。因此,利用面波的频散曲线,通过合适的反演方法,便可以获取地下介质的速度结构。假设面波是噪声的主要成分,利用F-K方法将空间-时间域的噪声记录转换到频率-波数域后,不同频率的面波在二维波数空间上会出现相应的峰值; 确定该峰值的位置即可得到波数,从而能够计算出不同频率面波的相速度,获取面波的频散曲线。如果研究三分量的连续噪声记录,便可以同时提取瑞雷波和勒夫波的频散曲线。
Okada(1987)利用F-K方法估算场地的瑞雷波频散曲线,并反演了场地的剪切波速度结构。Huang等(1990)利用最大似然法分析了台湾SMART地区的噪声记录,得到了该地区各个频率下的F-K谱,并获取了剪切波速度结构。Kavand等(2006)应用最大似然法研究了伊朗东南部Bam市区的噪声记录,获得了瑞雷面波频散曲线,并反演了该地区的剪切波速度结构。Tokeshi等(2006)针对两个场地,通过比较模拟波场和实际波场所获取的瑞雷波频散曲线,认为F-K方法用于提取频散曲线足够可靠。张碧星等(2005)采用F-K方法对瑞雷波多模式频散曲线进行了研究和分析,通过选取实际中经常碰到的3种分层介质模型,详细分析了接收道数目、源检距等参数对频散曲线的影响,发现当源检距大于半波长时利用F-K方法可以得到可靠的频散曲线。吴建明(2007)利用最大似然法估算了厦门2个不同场地的面波频散曲线,分析了窗函数、功率谱估算方法对F-K图像的影响。Picozzi等(2010)利用Richardson-Lucy(RL)和Tikhonov Regularization(TR)的2种反卷积方法从F-K图像中去除了台阵响应函数,获取了更高分辨率的F-K谱,并提取到了3.5~13Hz范围内的瑞雷波频散曲线。
2.4 评估台阵设计的优劣台阵作为地震观测网的重要组成部分,引起了地震学家的高度重视。出于不同的观测目的,如核爆识别,绘制区域地震活动图,监测远震等,全球范围内已经建设或正在筹建各种不同类型的台阵。台阵设计对于节约成本,确保各种监测目的实现的重要性不言而喻。作为一种重要的台阵数据处理方法,F-K谱的分辨率是衡量台阵布局是否合理的有效工具。
台阵布设中需要考虑到台阵形状、测点数量、孔径大小、台间距等多种因素,可以用台阵响应函数在频率-波数域的值来定量描述这些因素的影响。Schweitzer等(2002)比较了十字形的YKA和小孔径的ARCES两个台阵的响应函数,发现ARCES的几何形状比较完美,对不同方位角的分辨率很好,且旁瓣距离主瓣较远,但由于孔径较小,不容易识别具有微小差异的波数。而YKA由于孔径比较大导致台阵响应函数的主瓣很窄,在测量视速度时具有更高的分辨率,但是由于其几何形状的原因,在不同的方位角具有不同的分辨率。
吴建明(2007)利用模拟的平稳波场分析了5种形状的台阵,包括半径变化的圆形台阵、半径不变的圆形台阵、十字形台阵、混合型台阵及菱形台阵,考察了相应F-K谱的稳定性,据此评估了各个台阵的观测能力。在测点数量相同的情况下,十字形台阵和菱形台阵得到的F-K谱比圆形台阵及混合型台阵更为稳定。
3 讨论与展望本文介绍了F-K分析的基本原理及其各种改进方法,并综述了F-K方法在检测微弱信号源、噪声特征分析、提取面波频散曲线、台阵设计等4方面的应用。总体来说,F-K台阵处理方法具有较高的分辨率,其方法的不断改进也在拓宽它的应用领域。
(1) 本文总结了几种F-K分析方法,包括传统的聚束法和最大似然法,基于非相干平均法的F-K方法,利用Richardson-Lucy(RL)反卷积和CLEAN-PSF去除台站响应函数的F-K法。传统的聚束法和最大似然法的分辨率有限,容易漏检一些微弱的噪声源;而基于非相干平均法的F-K法能够拓宽所检测噪声源的频带,从而识别更多的微震噪声。然而,众多研究表明,台阵里有限的采样点及不合理的排列方式往往会限制F-K图像的空间分辨率及其对不同频率面波的分辨能力。以上几种方法均没有考虑到台阵布局对F-K谱的影响,利用它们对不规则的台阵进行F-K成像时会影响结果的分辨率。去除台阵响应函数的F-K分析方法能够弥补上述几种方法的不足,可以在一定程度上提高F-K成像的分辨率,使得如圆形、L型、十字型或随机分布的台阵都能够得到有效利用。
(2) 除了文中所述的应用之外,考虑到F-K分析能够降低地震等事件的识别下限,利用多个台阵便可以实现对微小地震的精定位。此外,F-K分析能够提高得微弱信号的信噪比,已经在定位近地表散射源中有了初步的应用,如何将其用于识别更多的反射波和散射波等微弱信号,从而拓宽地震台阵在地球内部的精细结构成像方面的应用,需要更深入的探索。
(3) 像其他大多台阵方法一样,F-K分析是基于平面波入射的假设,台阵下方的各向异性有可能会改变波前并破坏信号的相干性,从而改变F-K分析的结果。研究高频信号时采用的小孔径台阵的地下介质往往比较均匀,因而获得的入射波方位角较稳定,但由于高频微震信号源的变化,导致其视慢度值不稳定,可以通过滑动窗法获取高频噪声的时空变化特性;研究低频信号时需要台间距相对较大的台阵,视慢度值较稳定,但可能由于传播路径上的横向不均匀性而造成方位角的偏离,长时间叠加可能有助于稳定F-K图像的结果。
致谢: 审稿专家对本文提出了宝贵的修改意见和建议,谨表谢忱。| 师黎静, 2007, 基于地脉动的近地表三维速度结构探测和建模成像, 博士学位论文, 哈尔滨: 中国地震局工程力学研究所. http: //cdmd. cnki. com. cn/Article/CDMD-85406-2007128294. htm |
| 佟玉霞, 2002, 地震台阵的设计与数据处理研究, 博士学位论文, 北京: 中国地震局地球物理研究所. http: //cdmd. cnki. com. cn/Article/CDMD-85401-2004040012. htm |
| 吴建明, 2007, 利用F-K谱估算瑞利波频散曲线评估观测台阵的布设方案, 博士学位论文, 哈尔滨: 哈尔滨工业大学. http: //cdmd. cnki. com. cn/Article/CDMD-10213-2008193359. htm |
| 张碧星, 鲁来玉. 2005, 用频率-波数法分析瑞利波频散曲线. 工程地球物理学报, 2(4): 245–255. |
| Aster R C, McNamara D E, Bromirski P D. 2010, Global trends in extremal microseism intensity. Geophys Res Lett, 37(14). DOI:10.1029/2010GL043472. |
| Baggeroer A, Kuperman W, Mikhalevsky P. 1993, An overview of matched field methods in ocean acoustics. IEEE J Oceanic Eng, 18(4): 401–424. DOI:10.1109/48.262292. |
| Bensen G D, Ritzwoller M H, Shapiro N M. 2008, Broadband ambient noise surface wave tomography across the United States. J Geophys Res, 113(B5): B05306. DOI:10.1029/2007JB005248. |
| Bertero M, Boccacci P. 1998, Introduction to Inverse Problems in Imaging. Bristol: IOP Publishing |
| Birtill J W, Whiteway F E. 1965, The application of phase arrays to the analysis of seismic body waves. Philos Trans R Soc London A:Mathematical, Physical and Engineering Sciences, 258(1091): 421–493. DOI:10.1098/rsta.1965.0048. |
| Brenguier F, Campillo M, Hadziioannou C, et al. 2008a, Postseismic relaxation along the San Andreas Fault at Parkfield from continuous seismological observations. Science, 321(5895): 1478–1481. DOI:10.1126/science.1160943. |
| Brenguier F, Shapiro N M, Campillo M, et al. 2008b, Towards forecasting volcanic eruptions using seismic noise. Nature Geosci, 1(2): 126–130. DOI:10.1038/ngeo104. |
| Bromirski P D. 1999, Ocean wave height determined from inland seismometer data:implications for investigating wave climate changes in the NE Pacific. J Geophys Res, 104(C9): 20753–20766. DOI:10.1029/1999JC900156. |
| Bromirski P, Duennebier F. 2002, The near-coastal microseism spectrum:spatial and temporal wave climate relationships. J Geophys Res, 107(B8): 1–20. |
| Brooks L, Townend J, Gerstoft P, et al. 2009, Fundamental and higher-mode Rayleigh wave characteristics of ambient seismic noise in New Zealand. Geophys Res Lett, 36(23): L23303. DOI:10.1029/2009GL040434. |
| Bungum H, Mykkeltveit S, Kvaerna T. 1985, Seismic noise in Fennoscandia.with emphasis on high frequencies. Bull Seism Soc Am, 75: 1489–1513. |
| Capon J. 1969a, High-resolution frequency-wavenumber spectrum analysis. Proc IEEE, 57(8): 1408–1418. DOI:10.1109/PROC.1969.7278. |
| Capon J. 1969b, Investigation of long-period noise at the Large Aperture Seismic Array. J Geophys Res, 74: 3182–3194. DOI:10.1029/JB074i012p03182. |
| Cessaro R K, Chan W W. 1989, Wide angle triangulation array study of simultaneous primary microseism sources. J Geophys Res, 94: 15555–15563. DOI:10.1029/JB094iB11p15555. |
| Chevrot S, Sylvander M, Benahme S, et al. 2007, Source locations of secondary microseisms in western Europe:evidence for both coastal and pelagic sources. J Geophys Res, 112(B11): B11301. DOI:10.1029/2007JB005059. |
| Dougherty R P, Stoker R W, 1998, Sidelobe suppression for phased array aeroacoustic measurements, in Proceedings of the 9th AIAA/CEAS Aeroacoustics Conference, American Institute of Aeronautics and Astronautics Meeting Papers, 235~245. http://arc.aiaa.org/doi/abs/10.2514/6.1998-2242 |
| Doornbos D J, Husebye E S. 1972, Array analysis of PKP phases and their precursors. Phys Earth Planet Inter, 6: 387–399. |
| Essen H H, Kruger F, Dahm T, et al. 2003, On the generation of secondary microseisms observed in northern and central Europe. J Geophys Res, 108: 2506. DOI:10.1029/2002JB002338. |
| Friedrich A, Klinge K, Kruger F. 1998, Ocean-generated microseismic noise located with the Graefenberg array. J Seismol, 2(1): 47–64. DOI:10.1023/A:1009788904007. |
| Frosch R A, Green P E. 1966, The concept of the large aperture seismic array. Proc R Soc London A:Mathematical.Physical and Engineering Sciences, 290: 368–384. DOI:10.1098/rspa.1966.0056. |
| Gal M, Reading A M, Ellingsen S P, et al. 2014, Improved implementation of the fk and Capon methods for array analysis of seismic noise. Geophys J Int, 198(2): 1045–1054. DOI:10.1093/gji/ggu183. |
| Gal M, Reading A M, Ellingsen S P, et al. 2015, The frequency dependence and locations of short-period microseisms generated in the Southern Ocean and West Pacific. J Geophys Res, 120(8): 5764–5781. DOI:10.1002/2015JB012210. |
| Gal M, Reading A M, Ellingsen S P, et al. 2016, Deconvolution enhanced direction of arrival estimation using one- and three-component seismic arrays applied to ocean induced microseisms. Geophys J Int, 206: 345–359. DOI:10.1093/gji/ggw150. |
| Gerstoft P, Sabra K G, Roux P, et al. 2006, Green's functions extraction and surface-wave tomography from microseisms in southern California. Geophysics, 71(4.S): SI23–SI31. |
| Grevemeyer I, Herber R, Essen H H. 2000, Microseismological evidence for a changing wave climate in the northeast Atlantic Ocean. Nature, 408(6810): 349–352. DOI:10.1038/35042558. |
| Gupta I N, Lynnes C S, Wagner R A. 1990, Broadband F-K analysis of array data to identify sources of local scattering. Geophys Res Lett, 17(2): 183–186. DOI:10.1029/GL017i002p00183. |
| Halldorsson B, Sigbjornsson R, Schweitzer J. 2009, ICEARRAY:the first small-aperture, strong-motion array in Iceland. J Seismol, 13: 173–178. DOI:10.1007/s10950-008-9133-z. |
| Harjes H P, Henger M. 1973, Array-Seismologie. Z Geophys, 39: 865–905. |
| Haubrich R A, McCamy K. 1969, Microseisms:Coastal and pelagic sources. Rev Geophys, 7: 539–571. DOI:10.1029/RG007i003p00539. |
| Högbom J. 1974, Aperture synthesis with a non-regular distribution of interferometer baselines. Astron Astrophys Suppl Ser, 15: 417–426. |
| Horike M. 1985, Inversion of phase velocity of long period micro tremors to the S-wave-velocity structure down to the basement in urbanized areas. J Phys Earth, 33: 59–96. DOI:10.4294/jpe1952.33.59. |
| Huang W G, Yeh Y T. 1990, The characteristics of microtremors at the site of SMART1 array. Terrestrial Atmospheric & Oceanic Sciences, 1(3): 225–242. |
| Johnson D H, Dudgeon D E. 1992, Array signal processing:concepts and techniques. Simon & Schuster |
| Kavand A, Ghalandarzadeh A, Tabatabaii S, 2006, Determination of shear wave velocity profile of sedimentary deposits in Bam city(southeast of Iran)using microtremor measurements, Geoshanghai International Conference, 196~203. http://ascelibrary.org/doi/10.1061/40861%28193%2925 |
| Köhler A, Weidle C, Maupin V. 2011, Directionality analysis and Rayleigh wave tomography of ambient seismic noise in southern Norway. Geophys J Int, 184(1): 287–300. DOI:10.1111/gji.2010.184.issue-1. |
| Koper K D, de Foy B. 2008, Seasonal anisotropy in short-period seismic noise recorded in South Asia. Bull Seis Soc Am, 98: 3033–3045. DOI:10.1785/0120080082. |
| Koper K D, de Foy B, Benz H. 2009, Composition and variation of noise recorded at the Yellowknife Seismic Array, 1991-2007. J Geophys Res, 114(B10): B10310. DOI:10.1029/2009JB006307. |
| Koper K D, Hawley V L. 2010a, Frequency dependent polarization analysis of ambient seismic noise recorded at a broadband seismometer in the central United States. Earthquake Science, 23(5): 439–447. DOI:10.1007/s11589-010-0743-5. |
| Koper K D, Seats K, Benz H. 2010b, On the composition of Earth's short-period seismic noise field. Bull Seism Soc Am, 100(2): 606–617. DOI:10.1785/0120090120. |
| Krüger F, Baumann M, Scherbaum F, et al. 2001, Mid mantle scatterers near the Mariana slab detected with a double array method. Geophys Res Lett, 28: 667–670. DOI:10.1029/2000GL011570. |
| Kvaerna T, Doornbos D. 1986a, An integrated approach to slowness analysis with array and three-component stations. NORSAR Semiannual Tech Summary, 2(85/86): 60–69. |
| Kvaerna T, Ringdal F. 1986b, Stability of various f-k estimation techniques. Norsar Scient Rep, 1(86/87): 29–40. |
| Kvaerna T. 1989, On exploitation of small-aperture NORESS type arrays for enhanced P-wave detectability. Bull Seism Soc Am, 79: 888–900. |
| Lacoss R, Kelly E, Toksoz M. 1969, Estimation of seismic noise structure using arrays. Geophysics, 34(1): 21–38. DOI:10.1190/1.1439995. |
| Li L, Wang B S, Peng Z G, et al. 2016, Seismic detections of the 15 February 2013 Chelyabinsk meteor from the dense ChinArray. Earthquake Science, 29(4): 221–233. DOI:10.1007/s11589-016-0159-y. |
| Lucy L B. 1974, An iterative technique for the rectification of observed distributions. Astron J, 79: 745–754. DOI:10.1086/111605. |
| Nishida K, Kawakatsu H, Fukao Y, et al. 2008, Background Love and Rayleigh waves simultaneously generated at the Pacific Ocean floors. Geophys Res Lett, 35: L16307. DOI:10.1029/2008GL034753. |
| Okada H. 2003, The Microtremor Survey Method:Geophysical Monograph Series. Society of Exploration Geophysicists, 12: 1–5. |
| Okada H, Matsushima T, Hidaka E. 1987, Comparison of spatial autocorrelation method and frequency-wavenumber spectral method of estimating the phase velocity of Rayleigh waves in long-period microtremors. Geophysical Bulletin of Hokkaido University, 49: 53–62. |
| Picozzi M, Parolai S, Bindi D. 2010, Deblurring of frequency-wavenumber images from small-scale seismic arrays. Geophys J Int, 181: 357–368. DOI:10.1111/gji.2010.181.issue-1. |
| Richardson W H. 1972, Bayesian-based iterative method of image restoration. J Opt Soc Am, 62(1): 55–59. DOI:10.1364/JOSA.62.000055. |
| Ritter J R R, Jordan M, Christensen U, et al. 2001, A mantle plume below the Eifel volcanic fields, Germany. Earth Planet Sci Lett., 186: 7–14. DOI:10.1016/S0012-821X(01)00226-6. |
| Rost S, Thomas C. 2002, Array seismology:methods and applications. Rev Geophys, 40(3): 1008. DOI:10.1029/2000RG000100. |
| Rost S, Thomas C. 2009, Improving seismic resolution through array processing techniques. Surv Geophys, 30(4-5): 271–299. DOI:10.1007/s10712-009-9070-6. |
| Roux P, Sabra K G, Gerstoft P, et al. 2005, P waves from cross-correlation of seismic noise. .Geophys Res Lett, 32: L19303. DOI:10.1029/2005GL023803. |
| Richardson W. 1972, Bayesian-based iterative method of image restoration. J Acoust Soc Am, 62(1): 55–59. |
| Schmidt R O. 1986, Multiple source DF signal processing:an experimental system. IEEE Trans Ant Prop.AP, 34(3): 281–290. DOI:10.1109/TAP.1986.1143815. |
| Schweitzer J, Fyen J, Mykkeltveit S, et al, 2002, Seismic arrays:in new manual of seismological observatory practice-NMSOP. IASPEI, 481~532. |
| Shapiro N M. 2004, Emergence of broadband Rayleigh waves from correlations of the ambient seismic noise. Geophys Res Lett, 31(7): L07614. DOI:10.1029/2004GL019491. |
| Sijtsma P. 2007, CLEAN based on spatial source coherence. Int J Aeroacoust, 6(4): 357–374. DOI:10.1260/147547207783359459. |
| Stutzmann E, Schimmel M, Patau G, et al. 2009, Global climate imprint on seismic noise. Geochem Geophys Geosyst, 10(11). DOI:10.1029/2009GC002619. |
| Tkalĉićc H, Rawlinson N, Arroucau P, et al. 2012, Multistep modelling of receiver-based seismic and ambient noise data from WOMBAT array:crustal structure beneath southeast Australia. Geophys J Int, 189(3): 1680–1700. DOI:10.1111/gji.2012.189.issue-3. |
| Tokeshi J C, Karkee M B, Sugimura Y. 2006, Reliability of Rayleigh wave dispersion curve obtained from f-k, spectral analysis of microtremor array measurement. Soil Dynamics & Earthquake Engineering, 26(2-4): 163–174. |
| Toksöz M N, Lacoss R T. 1968, Microseisms:mode structure and sources. Science, 159(3817): 872. DOI:10.1126/science.159.3817.872. |
| Traer J, Gerstoft P, Bromirski P D, et al. 2012, Microseisms and hum from ocean surface gravity waves. J Geophys Res, 117: B11307. DOI:10.1029/2012JB009550. |
| Wax M, Shan T J, Kailath T. 1984, Spatio-temporal spectral analysis by eigenstructure methods. IEEE Trans Acoust.Speech and Signal Process, 32(4): 817–827. DOI:10.1109/TASSP.1984.1164400. |
| Wang H, Kaveh M. 1985, Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wideband sources. IEEE Trans Acoust.Speech and Signal Process, 33(4): 823–831. DOI:10.1109/TASSP.1985.1164667. |
| Wang Y, Li J, Stoica P, et al. 2004, Wideband RELAX and wideband CLEAN for aeroacoustic imaging. J Acoust Soc Am, 115(2): 757–767. DOI:10.1121/1.1639906. |
| Weber M, Wicks Jr C W. 1996, Reflections from a distant subduction zone. Geophys Res Lett, 23: 1453–1456. DOI:10.1029/96GL01322. |
| Westwood E. 1992, Broadband matched-field source localization. J Acoust Soc Am, 91(5): 2777–2789. DOI:10.1121/1.402958. |
| Wright C. 1972, Array studies of seismic waves arriving between P and PP in the distance range 90° to 115°. Bull Seismol Soc Am, 62: 385–400. |
| Zhan Z W, Ni S D, Helmberger Don V, et al. 2010, Retrieval of Moho-reflected shear wave arrivals from ambient seismic noise. Geophys J Int, 182: 408–420. |
 2017, Vol. 33
2017, Vol. 33


