2. 中国地震局地球物理研究所, 北京 100081
2. Institute of Geophysics, China Earthquake Administration, Beijing 100081, China
2008年汶川MS8.0地震是发生在大陆内部的高角度逆冲地震,造成了巨大的人员伤亡和财产损失。汶川地震后仅5年,龙门山断裂段南段又发生芦山MS7.0地震。虽然2次强震均发生在龙门山断裂带,但从余震定位结果看,芦山地震破裂与汶川地震破裂并未贯通,两者间存在一个“破裂空段”。该破裂空段引起地震学家们的广泛关注,陈运泰等(2013)指出,该“破裂空段”有发生MW6.8地震的潜在危险性。徐锡伟等(2013)和高原等(2013)的研究结果均认为需要密切关注该“破裂空段”再次发生破裂的危险。故该空段受到2次强震应力加载的情况究竟如何,其发生中强地震的概率如何,是急需解答的问题。
研究表明大地震产生的库仑破裂应力变化对后续地震发生位置和时间有较大影响(Harris,1998; Stein,1999; Das et al,1981; 周龙泉等,2008;万永革等,2010;单斌等,2012、2013;宋金等,2011、2014)。Dieterich(1979、1981、1994)提出了速率状态摩擦定律并推导出应力对区域地震活动的影响,其地震发生率模型被称为Dieterich模型。以库仑应力变化和区域背景地震活动等作为输入可估算研究区中强地震的累积发震概率,为区域地震危险性提供一定参考依据。2008年汶川地震发生后Toda等(2008)综合汶川主震的同震库仑应力变化和区域背景地震发生率认为龙门山断裂带南段6级地震发生率明显增加。邵志刚等(2010)采用粘弹性介质模型计算汶川地震产生的库仑应力动态变化并结合区域背景地震发生率分析了周边断层地震危险性,认为鲜水河断裂道孚-康定段和龙门山断裂带南段地震危险性较高。刘博研等(2013)计算了汶川地震同震库仑应力引起周边地震发生率变化,结果表明汶川地震的发生使芦山地震发震时间提前且需要密切关注鲜水河断层有发生6级地震的可能。2013年芦山地震再次发生,雷兴林等(2013)计算了汶川、芦山地震对周边的应力扰动影响,认为汶川地震确实对“破裂空段”处产生了应力触发影响,但截至2013年还未完全消除大邑地震的影响。徐晶等(2014)研究结果显示,汶川、芦山2次强震引起“破裂空段”处库仑应力显著增加。Liu等(2014)结合断层上地震矩和应力触发计算结果认为该“破裂空段”存在再次发生7级左右地震的可能。Jia等(2014)计算结果表明“破裂空段”受到明显应力加载,需密切关注该区域地震危险性。前人的研究工作大多集中于“破裂空段”处受到两次强震的应力加载方面,但尚无结合区域背景地震活动,估算在两次强震应力扰动作用下该空段处6级地震累积发震概率随时间变化的研究成果。本文首先基于分层粘弹性介质模型计算汶川和芦山2次地震对“破裂空段”处产生的累积库仑应力变化;进而引入Dieterich(1994)提出的速率状态摩擦定律并结合区域背景地震发生率给出“破裂空段”处6级以上地震的累积发震概率(图 1)。
|
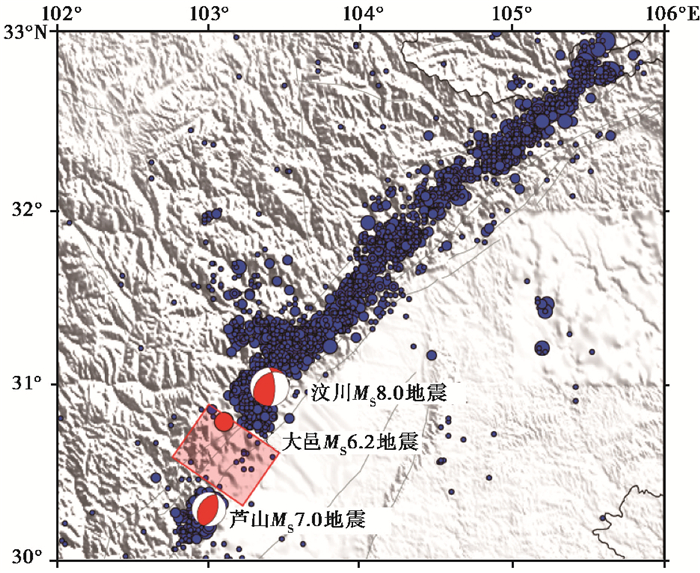
图 1 汶川地震后龙门山断裂带ML3.0以上地震分布(红色方框区域为“破裂空段”) 红色沙滩球为2008年汶川地震和2013年芦山地震震源机制解;蓝色圆圈为汶川地震后该地区ML3.0以上地震的震中;灰色线段为断层 |
库仑应力触发,是指前期发生地震引起的应力变化对研究区未来地震活动产生的促进或抑制作用(Harris,1998)。具体做法为将前期地震产生的应力变化张量投影到关注断层面和滑动方向上,计算库仑破裂应力变化ΔCFS。若库仑破裂应力变化为正,之前地震产生的应力变化会促使目标断层运动,即地震可能被触发,地震危险增大;反之,负的库仑破裂应力变化则会抑制断层运动,发生地震的可能性降低(Harris,1998; King et al,1994)。
库仑破裂应力变化ΔCFS定义为(Harris,1998;Stein et al,1992)
| $ \Delta CFS = \Delta {\tau _{\rm{s}}} + \mu \left( {\Delta {\sigma _{\rm{n}}} + \Delta p} \right) $ | (1) |
式中,μ为摩擦系数,Δτs和Δσn分别为断层面上的剪切应力和正应力,Δτs沿滑动方向为正,Δσn则定义为张开为正,Δp为孔隙流体压力变化。孔隙压力减少,则摩擦系数的效应可用μ′=μ(1-B)表示。其中,B为Skempton系数,范围为0~1(Rice,1992)。因此,式(1)变为
| $ \Delta CFS = \Delta {\tau _{\rm{s}}} + \mu '\Delta {\sigma _{\rm{n}}} $ | (2) |
当ΔCFS>0,则该应力变化有利于后续地震发生,否则不利于地震的发生。
1.2 基于Dieterich模型的地震发生率有很多摩擦本构关系可以用来解释岩石摩擦的实验室观测,其中与实验数据一致性较好且被广泛接受的是速率状态摩擦定律(Rate and State variable friction law,简称R-S模型),它能够解释诸如周期性黏滑、自持续周期性振荡、倍周期现象和混沌振荡等一系列实验室中观测到的现象(邵志刚等,2010)。R-S模型在地震研究中的重要应用之一便是模拟应力扰动后区域地震发生率的变化。例如Catalli等(2008)基于R-S模型,将库仑应力变化作为应力扰动来讨论强震对区域地震活动的影响,分析了1997年意大利安布里亚震群中各事件间的相互作用。
R-S模型的数学表达式为
| $ \tau = \left[ {{\mu _0} + A\ln \left( {\frac{V}{{{V_0}}}} \right) + B\ln \left( {\frac{{{V_0}\theta }}{{{D_{\rm{c}}}}}} \right)} \right]\overline \sigma $ | (3) |
式(3)中,A和B为经验常数,分别代表滑动速率变化对摩擦系数的短期直接影响和长期渐进影响。V和V0分别为滑动速率和背景参考滑动速率。μ为V=V0时的稳态摩擦系数。Dc为临界滑动距离,表示在经历速率变化后界面内颗粒重新接触而达到稳定状态所需距离。状态参数θ描述动摩擦系数随时间的渐变,θ有两种表达形式,分别为状态参数只随滑移距离改变的“滑移”形式和状态量与滑移速率有关的“慢度”形式,即
| $ \frac{{{\rm{d}}\theta }}{{{\rm{d}}t}} = - \frac{{V\theta }}{{{D_{\rm{c}}}}}\ln \left( {\frac{{V\theta }}{{{D_{\rm{c}}}}}} \right) $ | (4) |
| $ \frac{{{\rm{d}}\theta }}{{{\rm{d}}t}} = 1 - \frac{{V\theta }}{{{D_{\rm{c}}}}} $ | (5) |
研究表明,“滑移”形式更适合描述断层成核过程(Dieterich, 1979, 1981, 1994)。基于R-S模型,Dieterich(1994)进一步分析应力变化对区域地震活动的影响,得到地震发生率(Dieterich)模型,并分析了各相关参数对地震发生率结果的影响。地震发生率的计算公式为
| $ R\left( t \right) = \frac{r}{{\left[ {\exp \left( { - \frac{{\Delta CFS}}{{A\bar \sigma }}} \right) - 1} \right]\exp \left( { - \frac{t}{{{t_{\rm{a}}}}}} \right) + 1}} $ | (6) |
式(6)中,r为主事件前区域背景地震发生率,ΔCFS为主事件引起的库仑应力变化,A为摩擦本构状态参量,
邵志刚等(2010)指出,基于同震和震后每年库仑应力变化的地震发生率可以表示为
| $ {R_{{t_k}}} = \sum\limits_{t = 0}^k {R\left( {k - i} \right),\;\;} k = 0,1, \cdots ,n,\;{t_k} = {t_0} + k $ | (7) |
式(7)中,R可以由式(6)计算得到,k为首次应力加载后第k年,n为参与计算最大年限,i为主震发生后的年数,t0为主震发生年,tk为地震发生率计算年。
将地震发生率转化为至少发生一个地震的累积泊松概率P(Toda,2008),其公式为
| $ P = 1 - \exp \left( { - R} \right) $ | (8) |
本文将基于R-S模型并结合两次强震产生的库仑应力加载结果,计算龙门山断裂带“破裂空段”处6级地震的活动速率,最终得到该处累积发震概率随时间的变化。
2 累积发震概率 2.1 静态库仑应力基于分层粘弹性介质模型(徐晶等,2013),利用Wang等(2006)给出的PSGRN/PSCMP软件计算了汶川地震在芦山地震震中引起的同震库仑应力和震后累积效应。发震断层参数采用Ji等(2008)反演得到的汶川地震有限断层破裂模型数据,有效摩擦参数取0.4,计算深度为10km。计算结果表明汶川地震在芦山地震震中产生的同震库仑应力达0.016MPa,大于通常被认为能够有效促进后续地震发生的阈值0.01MPa(Harris et al,1998)。5年后震后粘弹效应不断累加,震后库仑应力达到0.021MPa。因此,汶川地震对芦山地震的发生存在明显应力触发作用,且震后粘弹效应不可忽略。
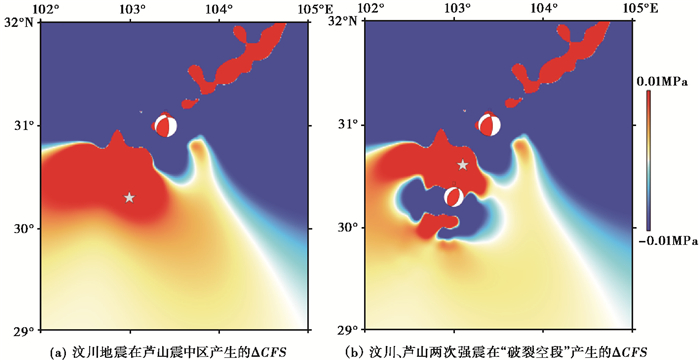
采用Ji等(2008)给出的汶川地震有限断层破裂模型反演结果和张勇等(2013)反演得到的芦山地震有限断层破裂模型对龙门山断裂带中南段“破裂空段”处应力扰动影响作了进一步研究。由于“破裂空段”面积较小,本文选择其中心位置来估算“破裂空段”受到的应力扰动情况。计算结果(详见图 2(b)和表 2)显示,“破裂空段”中心受到两次强震库仑应力的共同加载,累积应力变化不断增大;汶川地震产生的同震库仑应力为0.053MPa,芦山地震产生同震库仑应力为0.004MPa,至2030年两次地震同震和震后应力加载累积值达0.067MPa。
|
图 2 芦山震中区和“破裂空段”处库仑应力变化ΔCFS的空间分布 |
| 表 1 芦山震中处库仑应力变化(ΔCFS)和累积发震概率(PM)计算结果 |
| 表 2 “破裂空段”处库仑应力变化ΔCFS和累积发震概率PM计算结果 |
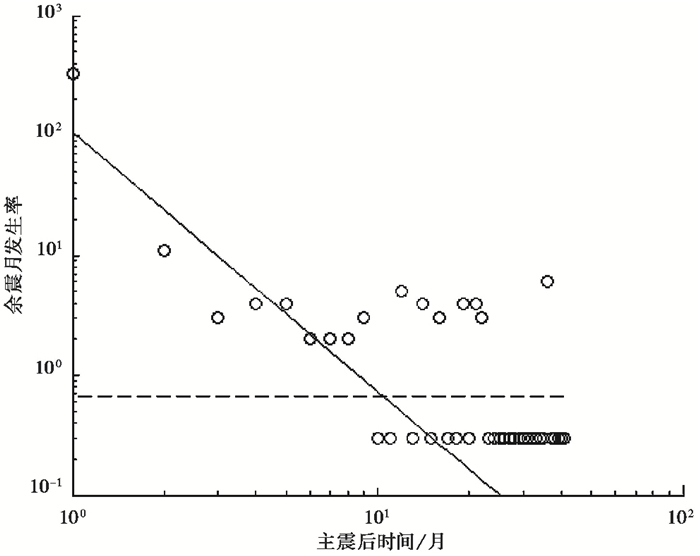
Toda等(1998)采用对数坐标线性拟合单位时间内余震个数随时间的变化,认为余震持续时间即为拟合线回到背景地震活动水平的时间。本文选取芦山震中周边100km范围计算背景地震活动水平,1970~2007年间共发生ML3.0以上地震299次,ML3.0以上背景地震月频度为0.67次。据中国地震台网测定,截至2016年12月芦山地震余震区共发生ML3.0以上地震385次,其中ML4.0~4.9地震50次,ML5.0~5.9地震13次。将其按单位时间(月)进行统计并在对数坐标系中进行线性拟合,余震频度衰减曲线回归至背景地震活动水平的时间即芦山地震余震持续时间(图 3)。由图 3可以看出,主震发生后地震序列的月频度不断衰减,拟合曲线较好地反映了余震衰减趋势。ML3.0以上余震发生率回归到背景场水平所需时间10.4个月,即芦山地震余震持续时间约10个月。利用相同的方法,申文豪等(2013)计算得到汶川地震余震持续时间约80年。由于两强震余震持续时间差异较大,ta值该如何选取需要进一步讨论。后续2.2.3节中对据不同ta值得到的累积发震概率结果进行比较,发现在2强震产生的应力扰动量值内,ta取值对累积发震概率的变化趋势和量级影响较小。考虑到我们计算目标震级为MS6,因此2.2.2节中累积发震概率ta值假设为10个月。需要指出的是,ta的这种取值方法,从物理上讲是弱化了汶川地震的可能影响。
|
图 3 2013年芦山地震后余震活动月频度随时间的衰减 圆圈为据余震数据统计得到的月频度值,虚线为背景地震活动水平 |
从1900年1月1日~2007年12月31日,龙门山断裂带仅发生了3次MS6以上地震,根据背景场地震活动性速率公式r≥M=N/Δt(其中N为发生大于震级M的地震次数,Δt为时间间隔)可以求出r≥6.0=0.028次/年。摩擦本构状态参量A和有效正应力
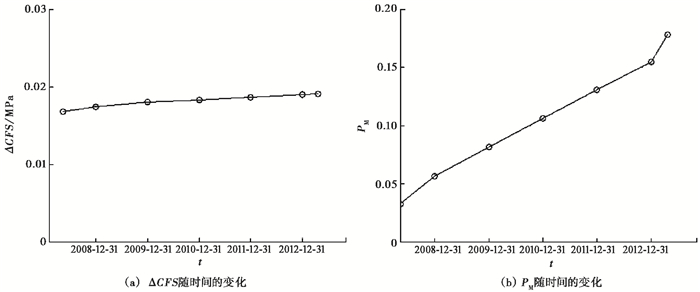
汶川地震发生后,芦山地震震中受到较强的同震和震后应力加载作用(表 1),根据(6)、(7)、(8)式计算得到芦山震中2008~2013年间发生大于6级地震的概率如图 4(b)所示。由图 4(b)可以看出,汶川地震产生的应力扰动引起芦山震中6级地震累积发震概率明显上升,芦山地震发生前6级地震累积发震概率达18%,最终导致芦山地震提前发生。这与刘博研等(2013)结论基本一致。
|
图 4 汶川地震发生后,芦山震中库仑应力ΔCFS变化和累积发震概率PM随时间的变化 |
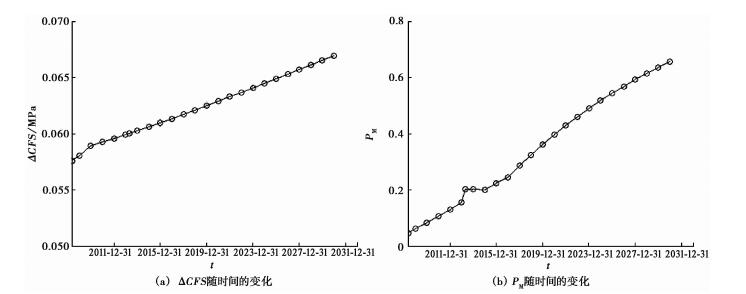
龙门山断裂带“破裂空段”的中心点累积发震概率计算结果如下所示(表 2、图 5(b)),由于同时受到汶川、芦山两次强震同震和震后持续加载作用,中心点处累积发震概率不断增大,至2030年底,6级地震累积发震概率达66%。基于上述结果,我们认为龙门山断裂带中南段“破裂空段”处仍存在发生中强地震的危险。
|
图 5 “破裂空段”处库仑应力ΔCFS变化和累积发震概率PM随时间的变化 |
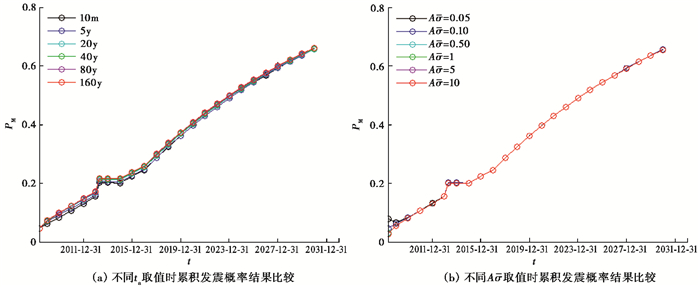
本文采用Toda等(1998)提出的对数坐标线性拟合法估算芦山地震余震持续时间约10个月。申文豪等(2013)采用相同的方法计算得到汶川地震余震持续时间约80年。由于2强震余震持续时间差异较大,ta值该如何选取需要进一步讨论。将“破裂空段”中心点作为研究对象,本文选取10个月~160年间不同值作为ta值分别计算累积发震概率并进行比较,结果显示在2强震产生的应力扰动量值内,ta取值不同对累积发震概率的变化趋势和量级影响较小(图 6(a))。截至2020年底,当ta取10个月时中心点累积发震概率结果为39.6%,而ta取160年时中心点累积发震概率结果为40.8%;结果显示余震持续时间取值越长,累积发震概率结果越大。
|
图 6 当ta和A |
本文计算过程中对摩擦本构状态参量A和有效正应力
2008年汶川8.0级地震、2013年芦山7.0级地震发生后,龙门山断裂带南段依然存在破裂空段,尺度规模相当于1次MW6~7级地震。其发震能力及当前的危险性引起广泛关注。针对此问题,本文首先采用分层粘弹性介质模型计算汶川、芦山2次强震在“破裂空段”处产生的同震和震后应力扰动。在此基础上,采用Dieterich(1994)提出的速率状态摩擦定律,结合龙门山断裂带6级地震活动背景地震活动水平,计算了“破裂空段”处6级地震累积发震概率随时间的变化。结果显示,“破裂空段”处6级地震累积发震概率随时间不断增大,至2030年底增至66%。
在计算过程中许多不确定性可能令累积发震概率结果存在一定误差。首先,“破裂空段”处1970年曾发生大邑MS6.2地震,它可能对“破裂空段”处的应力集中有一定减缓作用。再者,龙门山逆冲推覆构造带由龙门山后山断裂、中央断裂及前山断裂3条主干断裂带组成(张岳桥等,2013),汶川和芦山地震中间的“破裂空段”在地质构造上比较复杂,本文将其简化为一个中心点,且接收的断层参数主要参考芦山地震震源机制的做法可能会对最终计算结果产生一定影响。其次,分层粘弹性介质模型参数的选取,尤其是粘滞系数的设定会对强震产生的应力扰动结果造成一定误差,从而影响最终累积发震概率结果。同时1900年以来龙门山断裂带6级地震仅发生3次,对背景地震活动水平的估算结果也可能存在一定误差。
此外,本文用相同方法计算了汶川地震对芦山地震的扰动影响。结果显示,芦山震中受到汶川地震同震和震后应力的持续加载,震前6级地震累积发震概率达到18%;说明汶川地震产生的应力扰动可能促使芦山地震提前发生,这个结果与刘博研等(2013)的结论基本一致。因此我们认为,尽管结果可能存在一定误差,龙门山断裂带中南段“破裂空段”处仍存在发生中强地震的危险,且这种危险性随时间不断增大。
致谢: Jichen教授和张勇教授为本文提供了汶川和芦山破裂过程反演数据,汪荣江教授提供了PSGRN/PSCMP计算软件,审稿专家提出了中肯的修改意见和建议,在此表示衷心感谢。| 陈运泰, 杨智娴, 张勇, 等. 2013, 从汶川地震到芦山地震. 中国科学:地震科学, 43(6): 1064–1072. |
| 高原, 王琼, 赵博, 等. 2013, 龙门山断裂带中南段的一个破裂空段——芦山地震的震后效应. 中国科学(D辑), 43(6): 1038–1046. |
| 刘博研, 史保平, 雷建设. 2013, 汶川地震对芦山地震及周边断层发震概率的影响. 地震学报, 35(5): 642–651. |
| 雷兴林, 马胜利, 苏金蓉, 等. 2013, 汶川地震后中下地壳及上地幔的粘弹性效应引起的应力变化与芦山地震的发生机制. 地震地质, 35(2): 411–422. |
| 邵志刚, 周龙泉, 蒋长胜, 等. 2010, 2008年汶川MS8.0地震对周边断层地震活动的影响. 地球物理学报, 53(8): 1784–1795. |
| 单斌, 李佳航, 韩立波, 等. 2012, 2010年MS7.1玉树地震同震库仑应力变化以及对2011年MS5.2囊谦地震的影响. 地球物理学报, 55(9): 3028–3042. DOI:10.6038/j.issn.0001-5733.2012.09.021 |
| 单斌、熊熊、郑勇等, 2013, 2013芦山地震导致的周边断层应力变化及其与2008年汶川地震的关系, 43(6), 1002~1009. http: //kns. cnki. net/KCMS/detail/detail. aspx?filename=jdxk201306008&dbname=CJFD&dbcode=CJFQ |
| 申文豪, 刘博研, 史保平. 2013, 汶川MW7.9地震余震序列触发机制研究. 地震学报, 35(4): 461–476. |
| 宋金, 蒋海昆. 2011, 2010年4月14日玉树MS7.1地震对余震的触发研究. 中国地震, 27(4): 396–402. |
| 宋金, 周龙泉. 2014, 2014年于田MS7.3地震产生的静态库仑应力及对周边断层的影响. 中国地震, 30(2): 168–177. |
| 徐锡伟, 闻学泽, 韩竹军, 等. 2013, 四川芦山7.0级强震:一次典型的盲逆断层地震. 科学通报, 58(20): 1887–1893. |
| 徐晶, 邵志刚, 马宏生, 等. 2014, 汶川8.0级地震和芦山7.0级地震对周边断层的影响. 地震, 34(4): 40–49. |
| 万永革, 沈正康, 盛书中, 等. 2010, 2008年新疆于田7.3级地震对周围断层的影响及其正断层机制的区域构造解释. 地球物理学报, 53(2): 280–289. |
| 张勇, 许力生, 陈运泰. 2013, 芦山4.20地震破裂过程及其致灾特征初步分析. 地球物理学报, 56(4): 1408–1411. DOI:10.6038/cjg20130435 |
| 周龙泉, 马宏生, 夏红, 等. 2008, 2007年苏门答腊8.5级地震强余震库仑破裂应力触发研究. 地震, 8: 40–46. DOI:10.3969/j.issn.1001-8115.2008.03.008 |
| 张岳桥, 董书文, 侯春堂, 等. 2013, 四川芦山2013年MS7.0地震发震构造初步研究. 地质学报, 87(6): 747–758. |
| Catalli F, Cocco M, Console R, et al. 2008, Modeling seismicity rate changes during the 1997 Umbria-Marche sequence(Central Italy)through a rate and state dependent model. J Geophys Res, 88(B12): 0659–10370. |
| Dieterich J H. 1979, Modeling of rock friction:1. Experimental results and constitutive equations. J Geophys Res, 84((B5): 2161–2168. |
| Dieterich J H, 1981, Constitutive properties of faults with simulated gouge.//Carter N L, Friedman M, Logan G Meds, Mechanical behavior of crustal Rocks:The handin volume, Geophysical Monography Series, Volume 24. Washington DC:AGU, 103~120. http://adsabs.harvard.edu/abs/1981GMS....24..103D |
| Dieterich J H. 1994, A constitutive law for rate of earthquake production and its application to earthquake clustering. J Geophys Res, 99(B2): 2601–2618. DOI:10.1029/93JB02581. |
| Dieterich J H, Kilgore B D. 1996, Implications of fault constitutive properties for earthquake prediction. P Nati Acad Sci USA, 93(9): 3787–3794. DOI:10.1073/pnas.93.9.3787. |
| Das S, Scholz C. 1981, Off-fault aftershock clusters caused by shear stress increase. Bull Seism SocAmer, 71: 1669–1675. |
| Harris R A. 1998, Introduction to special section:Stress triggers.stress shadows.and implications for seismic hazard. J Geophys Res, 103: 24347–24358. DOI:10.1029/98JB01576. |
| Ji, C and Hays, G, 2008, Preliminary result of the May 12, 2008 MW7.9 eastern Sichuan, China earthquake. http://earthquake.usgs.gov/eqcentre/eqinthenews/2008/us2008ryan/finite_fault.php. |
| King G C P, Stein R S, Lin J. 1994, Static stress changes and the triggering of earthquakes. Bull Seismol Soc Am, 84: 935–953. |
| Jia Ke, Zhou Shiyong, Zhuang Jiancang, et al. 2014, Possibility of the Independence between the 2013 Lushan Earthquake and the 2008 Wenchuan Earthquake on Longmenshan Fault, Sichuan, China. Seismological Research Letters, 85: 60–67. DOI:10.1785/0220130115. |
| Liu Mian, Luo gang, Wang hui. 2014, The 2013 Lushan Earthquake in China Tests Hazard Assessments. Seismological Research Letters, 85: 40–43. DOI:10.1785/0220130117. |
| Rice J R, 1992, Fault stress states, pore pressure distribution, and the weakness of the San Andreas Fault, In:Evans B, Wong T Feds, Fault M echanics and Transport Properties of Rock, 475~503, London:Academic Press. http://www.sciencedirect.com/science/article/pii/S0074614208628351 |
| Stein R S. 1999, The role of stress transfer in earthquake occurrence. Nature, 402: 605–609. DOI:10.1038/45144. |
| Stein R S, King G C P, Lin J. 1992, Change in failure stress on the southern San Andreas Fault system caused by the 1992 magnitude=7.4 Landers earthquake. Science, 258: 1328–1332. DOI:10.1126/science.258.5086.1328. |
| Toda S, Lin J, Meghraoui M, et al. 2008, 12 May 2008 M=7.9 Wenchuan, China, earthquake calculated to increase failture stress and seismicity rate on three major fault systems. Geophysical Research Letters, 35: L17305. DOI:10.1029/2008GL034903. |
| Toda S, Stein R S, Reasenberg P A, et al. 1998, Stress transferred by the 1995 MW=6.9 Kobe Japan shock:Effect on aftershocks and future earthquakes probabilities. J Geophys Res, 103(B10): 24553–2456. |
| Wang R J, Lorenzo-Martin F, Ronth F. 2006, PSGRN/PSCMP-a new code for calculating co- and post-seismic deformation.geoid and gravity changes based on the viscoelastic-gravitational dislocation theory. Computers & Geosciences, 32(4): 527–541. |
 2017, Vol. 33
2017, Vol. 33


