2. 安徽省蒙城地震台, 安徽亳州 233527;
3. 安徽蒙城地球物理国家野外科学观测研究站, 安徽亳州 233527;
4. 山东省地震局, 济南 250021;
5. 中国地震局地壳应力研究所, 北京 10008
2. Mengcheng Seismostation, Anhui Province, Bozhou 233527, China;
3. Anhui Mengcheng National Geophysical Research Station field of Scientific Observation, Bozhou 233527, China;
4. Earthquake Administration of Shandong Province, Jinan 250014, China;
5. Institute of Crustal Dynamics, China Earthquake Administration, Beijing 100085, China
地磁场是地球固有的基本属性,伴随着地球形成演化的全过程,成为地球生物圈(包括人类)生存的重要环境条件(徐文耀,2009)。而在地震孕育的过程中存在磁效应变化,故地磁观测数据已用于地震预测研究(黄雪香等,1999;林云芳,1990),地磁观测是地震前兆观测的重要手段之一。
经过“九五”数字化建设、“十五”数字化改造和“十一五”背景场建设,国家地磁观测台网先后完成各区域地磁台网相对记录仪的数字化升级改造,同时完成3个地磁台阵建设,目前在线运行239套分采样或秒采样数字化相对记录仪。至今已运行十几年,产出了大量数据,但在运行过程中,由于校时不及时或校时设备故障等原因,造成仪器记录数据对应时间与实际时间不一致,给数据的应用造成了一定困扰。
地磁场是一个大范围甚至全球相关性很强的物理量,在观测中对数据时间精度的要求很高,对地磁脉动的研究需要将地磁场在全球的传播时间对比;在地磁暴和地磁亚暴分析特别是急始型磁暴分析中,对时间的一致性要求很高;在地震预测研究中关于地磁变化及地磁同震现象(T.Iyemori et al,1996)等研究中,地磁变化出现时间直接影响研究过程和结果;此外,数据预处理的自动化是未来发展必然趋势,时间同步性的破坏也将影响对干扰的判断,特别是影响范围大的干扰如高压直流输电干扰(陈俊等,2014)。地磁观测数据中因时间的精度不够高,在一定程度上会影响数据的分析利用,干扰其与全球观测结果的相关分析,甚至可能对地震活动的预测分析造成误导,因此观测数据的时间精度是影响数据质量的一个重要因素。
在海洋磁力测量(即在海上进行地球磁场测定)中,常采用经度差法、相关系数法和同步比对法计算观测数据时间与实际时间差,进行时差改正,这些方法各有优缺点。经度法是目前最常用的方法,优点是原理简单,计算方便,只需知道校正点与标准时间测点的地理经度差即可,且在海洋磁力测量中时差校正主要应用于改进日变幅度的测量,时差改进对该应用影响较小,姚俊杰等(2005)验证了经度差法的不完善性,其误差达11min,认为其精度有待提高。相关系数法有助于提高精度,该法的优点是对短距离台站间的改进效果好,利用秒采样数据的误差能缩小到10s,同时指出相关系数法受限于台间距离的影响;同步比较法是利用日变极值点比对的方法对时差进行校正,王磊等(2011)研究认为同步对比法和相关分析法能反映站间真实时差,利用秒数据所得结果的精度在80s内,优于经度法,但仍然受地方时即经度影响。上述方法可以借鉴到我国地磁观测台网固定台站的时钟差检测与校正中来,但固定台网所覆盖范围广,在方圆数千千米范围内非均匀分布,受地方时影响的限制,需要作进一步改进。
本文根据地磁扰动数据全球同步变化的特性,通过地磁扰动区间内把出现数据极大值和极小值的时间分别进行比对的方法,检查数据时钟的精度,获得数据时钟的校正值,本文将该方法称为扰动区间极值比对法,该方法不受地方时(即经纬度)的影响。
1 地磁观测数据的变化特征地磁场包括基本磁场和变化磁场两部分。基本磁场是主要的,起源于地球内部,比较稳定,属于静磁场。变化磁场包括地磁场的各种短期变化,起源于地球外部,相对较弱,受太阳的活动影响比较大(徐文耀等,2005;岳庆祥等,2004)。地球变化磁场可分为平静和扰动两大变化类型,其平静变化保持正常日变形态的日子称为磁静日(图 1,本文数据时间为世界时即UT),其变化曲线表现呈规则的日变形态,其扰动变化则打破了正常日变形态,这时称为磁扰日(图 2)。
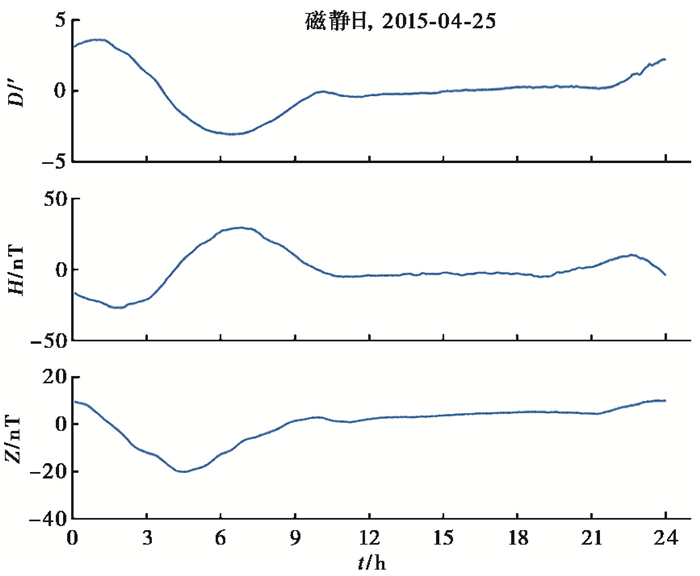
|
图 1 磁场平静变化形态 |

|
图 2 磁场扰动变化形态 |
为对比考察磁静日、磁扰日大范围内的变化特征,我们选取了一条经度链(由北至南为满洲里MZL、红山LYH、蒙城MCH、南昌NCH、泉州QZH,最大经度差3.8°)和一条纬度链(从东向西为红山LYH、榆林YUL、嘉峪关JYG、且末QIM、喀什KSH,最大纬度差2.4°),各取5个台站,分别绘制静日曲线(图 3)和扰日曲线(图 4),其中D为磁偏角,H为地磁场强度的水平分量,Z为地磁场强度的垂直分量。从图中可见,磁静日中纬度链上与经度链上的台站数据曲线均呈现规则的日变形态。纬度链台站(图 3(a))D、H、Z变化自东向西存在明显的地方时变化,日变幅相当;经度链台站(图 3(b))D分量变化无相位差异,自南向北日变幅逐渐增大,H、Z分量随着纬度由低向高逐渐相位滞后,日变幅相差不大,且各台站Z分量形态差异较大,说明其还受其他因素的较大影响。可见D分量随经度变化存在相位差异,随纬度存在日变幅不同;H、Z分量相位同时受到经度(地方时)和纬度差异的影响,除此之外,Z分量受其他因素影响较大。而在磁扰日即磁场存在较大扰动情况下,磁扰时间段(2015年3月25日9:00~21:00)各分量都存在同时性的扰动变化,即该段时间记录的数据曲线形态受扰动与地方时的影响较小,不存在相位上的差异,其中H分量表现尤其明显。
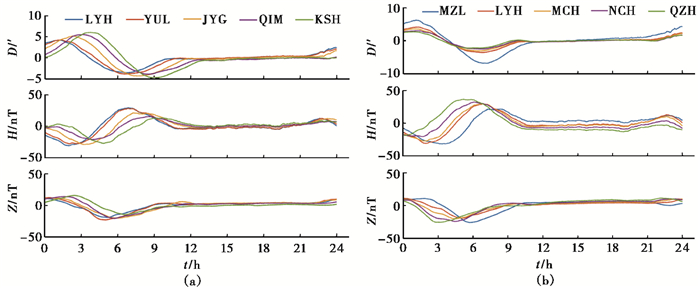
|
图 3 磁静日多台观测曲线形态(2015-04-25) (a)纬度链上台站数据变化,(b)经度链上台站数据变化 |
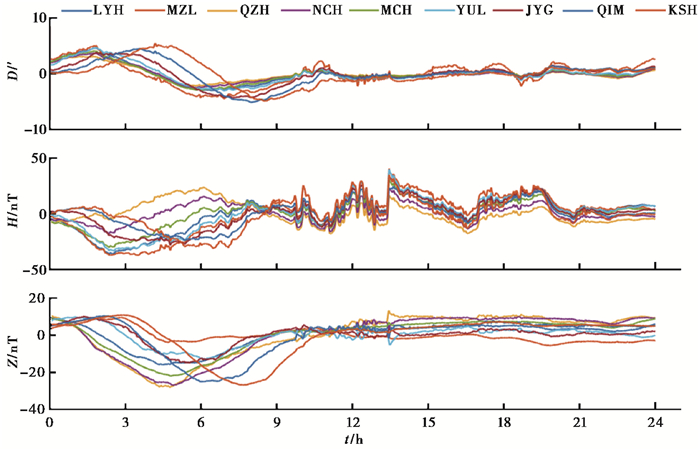
|
图 4 磁扰日多台观测曲线形态(2015-3-25) |
全国地磁观测台网在线运行的记录仪包含多种型号,如质子旋进矢量磁力仪FHD系列、磁通门磁力仪GM系列、Overhauser磁力仪GSM系列等,仪器类型较多,各种仪器采用的授时方式和途径存在差别,主要有2种对时方式,GM系列采用GPS授时,FHD系列和GSM系列仪器时钟精度较高,理论授时误差为1s/月,采用人工授时。
为了了解时钟差的来源,笔者针对不同授时方式仪器分别挑选2015年3月25日存在较大时钟差的两套仪器——大武台GM4-XL(快5min)和固原台FHD-1(慢7min)进行分析。通过人工统计,向前追踪其时钟差变化规律。从统计结果(图 5)可以看出,大武台(DAW)从3月2日开始每隔5~6天仪器时钟差变大1min,由此可推测该钟差变化应为仪器GPS校时失败或校时设备故障,而仪器自身时钟误差较大造成;固原台(GYH)从2月25日~3月26日时钟差保持在7min,稳定性较好,3月27日9:00后时钟差变为0min,因为经过了人工校时操作,笔者继续对该仪器时钟变化向前追溯,在2014年12月26日时差变为6min,由此可知FHD系列时钟差是因为数月时间不校时或人工授时不准造成的。
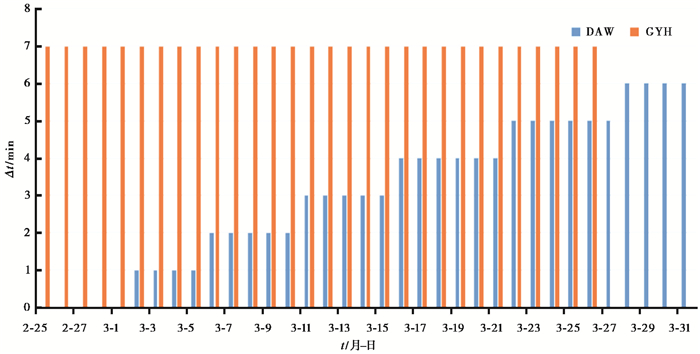
|
图 5 2015年2月25日~3月31日时钟差变化趋势 |
磁情指数K是用来描述每3h段(一天分为8个时段)的地磁扰动强度指数,表征磁场扰动强度的定量分级指数K值越大,表示磁场扰动越剧烈,一般当K>3时,说明存在较强的磁场扰动。磁场扰动是在大区域甚至全球范围内同步发生的,利用该特性,通过比对大区域内多套仪器或所有仪器的扰动开始、结束时间或极值时间,人眼可以很容易发现记录数据不一致(图 6)。由图 4可看出,H分量的扰动是最明显的。从9:00~18:00磁扰数据的极值点中,能很清楚的看出DAW(大武台)的数据时钟超前,另3套仪器(红山、满洲里和蒙城)的数据完全同步。由此可以推测,只需比对全台网所有仪器磁扰区间极值点时间重合度即可以提取出数据时钟存在错误的仪器,并计算出数据时钟与实际时钟差值,即扰动区间极值比对法(图 7)。
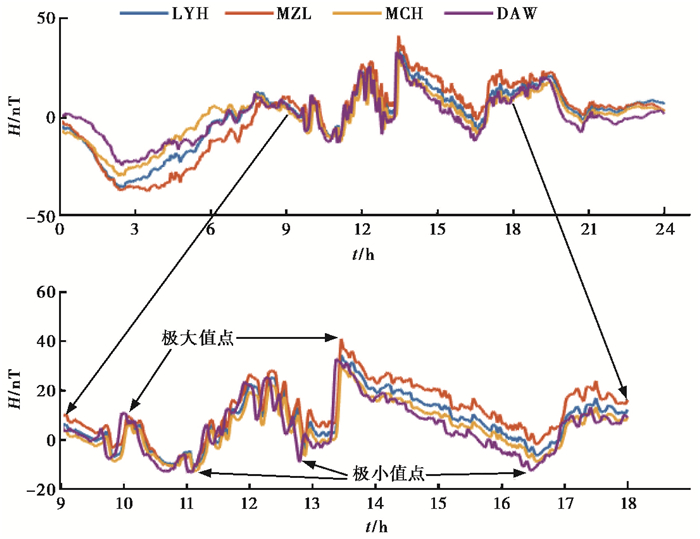
|
图 6 扰动期间多台站曲线的对比 |
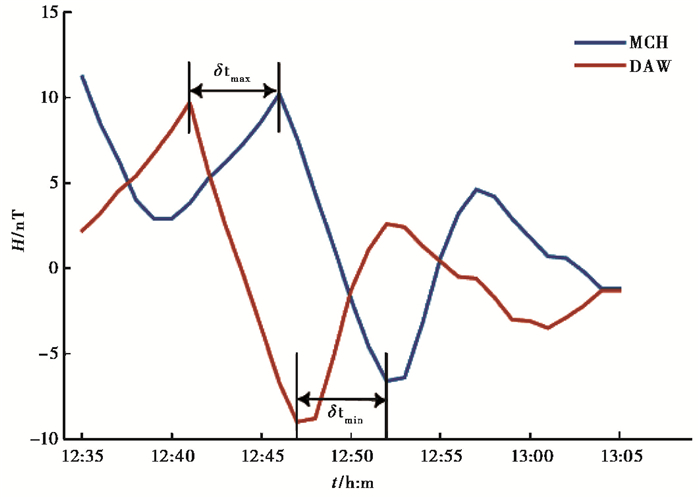
|
图 7 两台站观测到的同步扰动曲线 |
如图 7,假设MCH和DAW两台站仪器记录数据时间分别为TMCH(t)和TDAW(t),其中MCH与标准时间重合,那么台站DAW记录时间与实际时间的差δt可以由扰动区间的极大值δtmax和极小值δtmin出现的时刻差异的平均值得到,即
| $ \left\{ \begin{array}{l} \delta {t_{\max }} = {t_{{\rm{MCH}}\max }} - {t_{{\rm{DAW}}\max }}\\ \delta {t_{\min }} = {t_{{\rm{MCH}}\min }} - {t_{{\rm{DAW}}\min }} \end{array} \right. $ | (1) |
那么,台站DAW记录数据时间与标准时间差可表示为
| $ \delta t = \left( {\delta {t_{\max }} + \delta {t_{\min }}} \right)/2 $ | (2) |
由于一套仪器所测各分量共用同1个时钟,故任一分量数据时钟错误即表明所有分量的数据时钟是错的。据此可得到时间准确性检查方法的实现流程(图 8)。
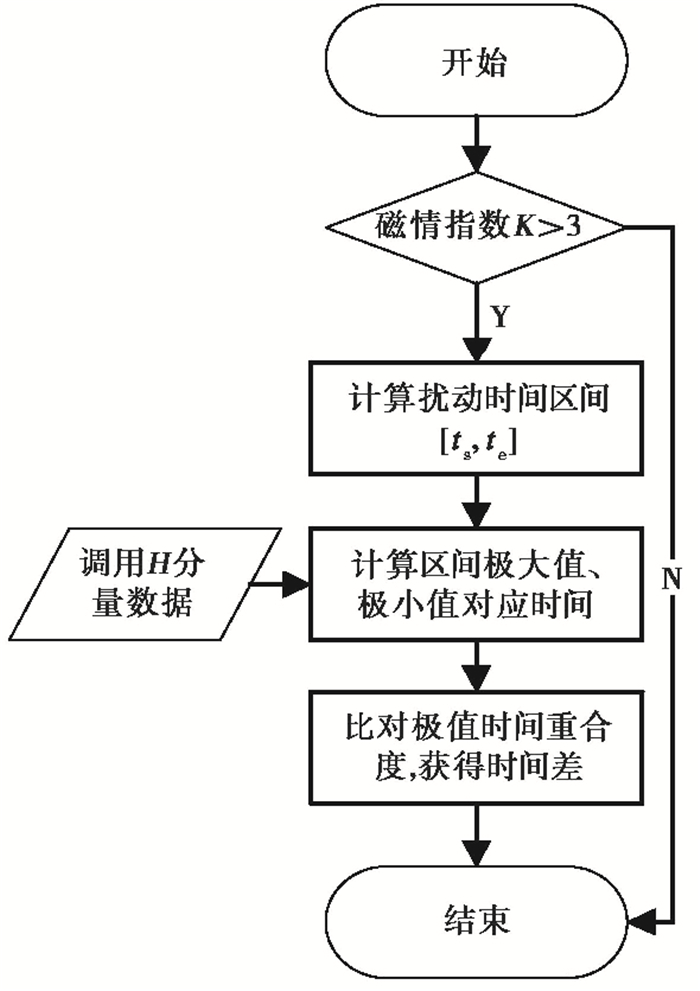
|
图 8 时钟准确性检查方法流程 |
从图 8可知,在该方法中,首先利用K指数确定扰动区间,确定极值计算区间;然后调用确定区间的全台网地磁数据计算极大值和极小值时间点;再由极值点时间重合最多的仪器时间确定标准时间——因台网现有仪器绝大多数采用GPS校时,而人工校时仪器时钟数月稳定,故假设多数重合时间点为标准时间点;最后使用各套仪器记录数据的极值点与标准时间进行比对,从而得到各仪器记录时间与实际时间的差。其中极值点的确定和标准时间的计算是该法的两个关键节点,具体步骤如下:
(1) 数据获取 扫描选择月K指数表中所有仪器的K指数,提取K>3的3h时间段,获得扰动起始时间列表,并拆分为0.5h时间区间([ts, te])列表tList0,记录区间开始时间ts和结束时间te,然后读取所有仪器H分量对应时间区间的预处理分数据。
(2) 数据处理 去除单点尖峰,排除单点干扰后,计算tList0中各时间区间中所有仪器的极大时tmax、极小时tmin,选择tmax和tmin为非区间边界值的时间区间作为统计时间区间,获得极大时极小时列表tList,然后统计极大、极小时点重复率,重复率最大的极大、极小时即为标准时间值t。
(3) 时间比对与校正 由步骤(2)得到了极时列表tList(所有仪器的极大、极小时)和标准时间值t,由公式(1)和(2)进行所有仪器时间与标准时间值t的比对,获得钟差δt。
得到δt后,可对各台仪器数据进行时间校正,即把数据前后平移,δt>0时,数据向前平移;δt<0时,数据向后平移,即可得到时间准确的数据。
4 实验结果利用国家地磁观测台网2015年2月25日~3月31月间的预处理分数据对该方法进行检验,程序自动筛选了3月25日的数据——考虑到全台网秒采样仪器与分钟采样仪器(约120套)并存的现状,且均能产出分数据,故本文研究方法针对分钟数据进行时钟校正研究,以增强方法的通用性。以1min时间精度进行检查计算(表 1、图 9),全台网总共239套仪器,只有8套仪器判断错误,时间判断准确率达96.65%,且未检出仪器均只存在1min时差,即对时差大于1min的异常检出率100%;程序自动检测出36套仪器存在时钟异常,经人工核实,均为异常仪器;在检出异常仪器中,除了2套时间差较大之外,检出时间差与实际时间差最多相差1min,即针对检出时间异常仪器能提供精度达到2min校正时间的准确率为94.44%。
| 表 1 时间异常自动检出情况统计 |
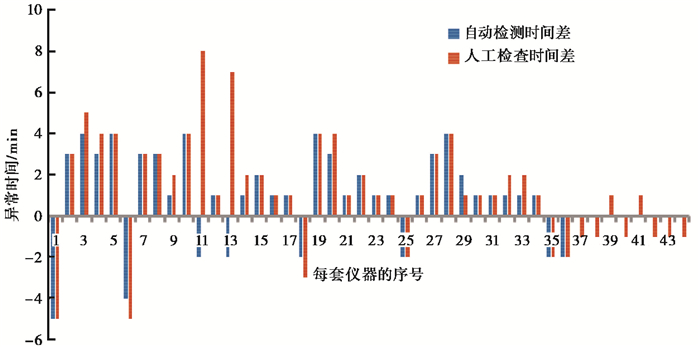
|
图 9 时间异常仪器自动检查与人工检查结果对比 |
在地磁场观测中,为了实现数据时钟精度自动检查而采用的扰动区间极值比对法,充分利用地磁扰动变化的大区域同步特性,该方法有效避免了地方时即经纬度的影响。经实验,得到了很好的检查效果,该方法检查全国地磁观测台网239套仪器产出数据的时钟精度,对这些仪器中分数据时钟精度误差大于1min的仪器检出率达100%,且对94.44%的检出仪器能提供较准确的校正时间,校正误差不大于2min。证明该方法是实现地磁台网大量仪器时钟精度的自动监控检查的可靠技术手段,可在此基础上进一步实现软件自动提醒台站员工及时检查仪器校时与设备状态;可为数据使用者了解数据时钟总体状况提供参考依据,为扰动日期数据时差的校正提供了较大的便利,能有效减轻台网管理者和科研工作者数据校核和数据清理的工作量;特别是在磁暴研究中,该方法可提供很好的钟差校正数据。
扰动区间极值比对法主要针对我国地磁观测台网仪器时钟检查自动化而设计,采用本台网日常产出的3小时磁情指数K作为扰动区间判断依据,主要为便于检查系统的实现。若采用每小时磁暴环电流指数(Dst)判断扰动区间,将使扰动区间定位更加精确,提高检查效率,但目前我国暂无Dst指数产出;如果采用更长的计算窗长,解决大幅度异常时间的改进精度问题,本方法的准确度将进一步提升;该方法有效避开了地方时影响,但限于扰日数据的检查和校正,静日数据的自动检查和校正有待进一步研究。
致谢: 本文利用数据由国家地磁台网中心提供,在此表示感谢;特别感谢匿名审者对完善本文提供的宝贵意见。| 陈俊, 蒋延林, 张秀霞, 等. 2014, 地磁台网高压直流输电干扰判断系统设计. 地震地磁观测与研究, 35(3/4): 270–274. |
| 黄显良, 郁建芳, 戚浩, 等. 2016, 安徽霍山窗中小地震活动与精定位研究. 地震工程学报, 38(2): 236–241. |
| 黄雪香, 张美仙, 林云芳, 等. 1999, 华北北部几次中强地震前的地磁前兆特征. 地震, 19(2): 168–178. |
| 林云芳. 1990, 大同-阳高地震前后地磁异常变化及其认识. 地震, 4: 27–36. |
| 王磊, 边刚, 任来平, 等. 2011, 时差对海洋磁力测量地磁日变改正的影响分析. 海洋测绘, 31(6): 39–41. |
| 徐文耀. 2009, 地球电磁现象物理学. 北京: 中国科学技术大学出版社. |
| 徐文耀, 魏自刚, 夏国辉. 2005, 2000年中国地区地磁场长期变化的区域特征. 地球物理学报, 48(3): 551–560. |
| 姚俊杰, 孙毅, 刘国斌, 等. 2005, 地磁日变数据时间同步相关系数分析. 海洋测绘, 25(6): 15–17. |
| 岳庆祥, 于洪池, 吴江星, 等. 2004, 长春地磁台地磁场长期变化基本特征. 地震地磁观测与研究, 25(2): 75–78. |
| Iyemori T, Kamei T, Tanaka Y, et al. 1996, Co-seismic geomagnetic variations observed at the 1995 Hyogoken-Nanbu earthquake. Journal of Geomagnetism & Geoelectricity, 48(8): 1059–1070. |
 2017, Vol. 33
2017, Vol. 33



 , 滕云田1, 王秀英5
, 滕云田1, 王秀英5