震级表征地震的强弱,是描述地震的基本参数之一,也是地震预测研究中的重要参数之一(陈运泰等,2000、2004)。用震级度量地震的大小,简便易行、通俗实用。但最大的缺点是存在震级饱和效应。矩震级是一个描述地震绝对大小的力学量,是目前度量地震大小、且不存在饱和问题的最理想的物理量(高景春等,2011;杨晶琼,2013)。1977年,Kanamori定义了地震的矩震级MW,并给出了地震矩、矩震级和地震波能量三者的关系(Kanamori,1977a、1977b)。1981年,Dziewonski等(1981)完成了矩张量反演矩心矩张量解(Dziewonski等,1981;Sipkin,1982),实现了快速发布矩震级MW。美国地质调查局在2001年制订的“USGS”中明确要求将矩震级作为向政府机关和社会公众发布的首选震级。MW在一定震级范围内能与常规的面波震级衔接起来(刘瑞丰等,2004)。最新《地震震级的规定》(GB17740-2017)中规定,矩震级MW为发布的首选震级。2008年汶川地震后,地震应急工作对地震台网的产出提出了更高要求,经过几年的发展,使得震源机制解、矩震级加入传统目录成为可能(康英等,2015),为矩震级的日常产出打下了坚实的基础。
内蒙古中西部地区(E104°~115°;N36°~42°),地震构造复杂,区域特征差异十分明显,中强地震频发(曹刚,2001)。1970年以来,先后发生了1976年和林格尔6.3级、巴音木仁6.2级地震、1979年五原6.0级等一系列中强地震(孙加林等,1998)。目前为止,内蒙古地区没有开展中小地震矩震级的研究工作。本文利用内蒙古测震台网记录的2008~2016年3月的近场数字地震波形资料,采用多台联合反演方法计算得到中小地震的震源谱参数(刘芳等,2007;杨晶琼等,2010),从而获得了这些地震的地震矩M0、矩震级MW和应力降σ。用线性回归方法研究近震震级ML和MW、MW和σ的关系,以期为大震速报、地震编目和地震学相关研究提供参考。
1 资料选取及数据处理选取内蒙古中西部地区202次地震波形资料,进行“S窗”数据预处理,获得该区域的品质因子Q(f)值和台站场地响应,按照“信噪比大于2,每个地震记录台数N≥4”的原则(刘丽芳等,2010;杨晶琼等,2013),最终得到符合要求的182次地震的震源参数(地震矩、矩震级和应力降)。
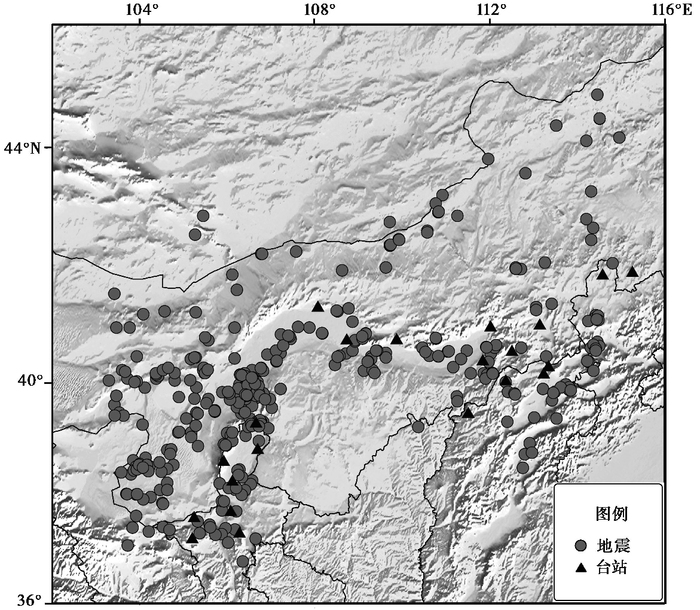
1.1 资料选取内蒙古中西部地区由22个测震台站(内蒙古8个,河北1个,宁夏9个,山西4个)组成,除了宁夏台网的TLE和LWU台基为粘土,其余20个台站均为基岩台,用24位的EDAS-24 IP、EDAS-24GN6、EDAS-24L6、SMARRT-24R、CMG-DM24共5种类型数据采集器,采用地面超宽带、甚宽带,井下甚宽带、宽带4种类型的地震计,地震计地动速度响应频带为60s/ 50Hz。地震计有效动态范围优于130dB,每秒100点采样,数据采集器动态范围优于130dB。本文选取2009~2016年3月ML≥2.8的202次地震事件进行矩震级测定(图 1),从图中可看到,202次地震基本覆盖内蒙古中西部地区,基本可以反映该区域的地质构造特征。
|
图 1 2009~2016年3月内蒙古中西部地区202次地震和台站的分布 |
在进行矩震级测定前,要截取“S窗”。“S窗”定义是从S波起始至包含S波总能量90%的时间段。然而,“90%S波总能量”只是一个理论上的概念,具体读取时是采用人机结合“目测读取”来实现。读取震相到时和“S窗”时,选用经验较丰富的分析人员,且固定人员进行读取,以最大限度地避免读取误差。
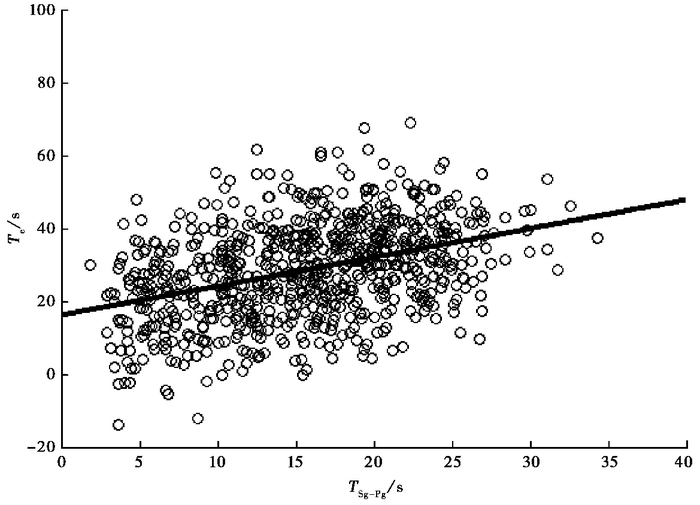
依据上述读取原则,确定了182次地震的震相到时和“S窗”的结束时间,得到了“S窗”长和Sg-Pg的拟合关系(图 2),从图 2可知,拟合呈线性,均方根为0.11。“S窗”长和Sg-Pg的关系式为
|
图 2 “S波窗”长和Sg-Pg的线性关系 |
| ${T_{{\rm{se}}}} - {T_{{\rm{sf}}}} = 0.78\left( {{T_{{\rm{sg}}}} - {T_{{\rm{pg}}}}} \right) + 16.3$ | (1) |
式中Tse表示“S窗”的截止时间;Tsf表示Sf到时,Tpg表示Pg到时。
Sf为首个S波震相的到时:①如果该台有Sn到时,Sf等于Sn到时;②如果没有Sn,Sf等于Sg到时。
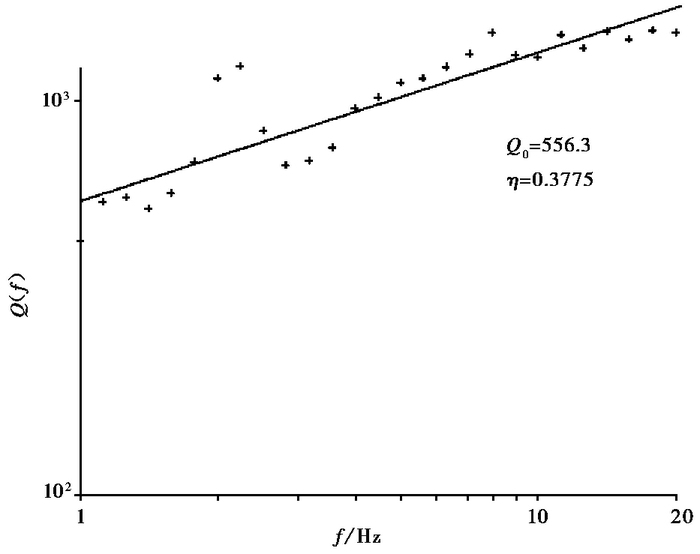
1.2.2 Q值和台站场地响应的确定在进行矩震级计算前,要确定研究区的品质因子Q(f)和22个台站的场地响应。选取2009~2015年3.0≤ML≤4.7、波形较清晰的46次地震波形资料用于反演品质因子Q(f)。在1~20Hz范围内,品质因子Q(f)值与频率有较好的线性关系(图 3、式(1))
|
图 3 品质因子Q(f)拟合图 |
| $Q\left( f \right) = {Q_0}{f^n}$ |
当f=1Hz,Q0=556.3,介质吸收系数η=0.3775时,则
| $Q\left( f \right) = 556.3{f^{0.3775}}$ | (2) |
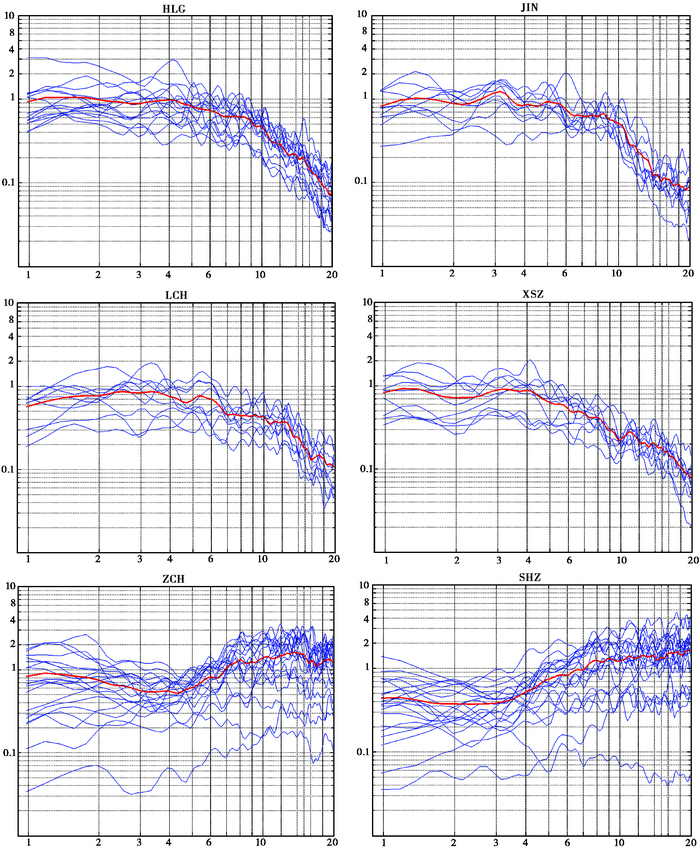
依据上述品质因子Q(f)得到了22个台站场地响应,其中,宝昌、凉城、和林格尔、集宁、西山嘴、康保、牛首山、香山、中卫、同心、盐池、陶乐、银川、石嘴山共14个台站场地响应在1附近,随频率的变化,场地响应变化波动较小;灵武、宝和少台场地响应为轻微的放大效应。分析可知,灵武台放大效应是由于其土质层较为松软(金春华等,2012),宝和少台放大效应是因为其周围覆盖层较厚。包头、二连浩特台场地响应有轻微的衰减效应,可能是台站基岩较为坚硬或与台站所处的地质环境影响有关(王鑫等,2015)。大同、镇川台场地响应在低频时呈轻微衰减,高频时呈放大效应。右玉、偏关台场地响应,低频在1附近,高频则有明显放大效应。图 4给仅出了HLG、JIN、LCH、XSZ、ZCH和SHZ的场地响应。
|
图 4 6个台站场地响应 |
综上所述,22个台站中有14个台站场地响应在1附近,占总数的63.6%;4个台站场地响应有轻微的放大或衰减效应,占总数的18.2%;4个台站场地响应在高频时呈放大效应,占总数的18.2%。分析认为,22个台站场地响的变化结果基本保证了震级的测定精度。
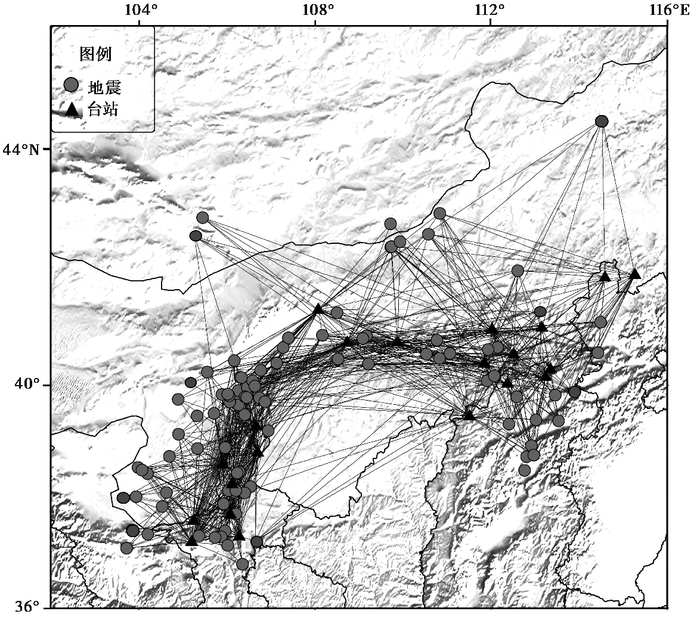
基于“S窗”选取结果、品质因子和场地响应的结果,最终得到满足条件的182次地震的震源参数,地震和台站射线见图 5。
|
图 5 182次地震的震中分布和台站射线 |
“地震是霎那间照亮地球内部的一盏明灯”,提取和分析地震波所携带的丰富信息是克服地球内部“不可见性”的最重要途径。地震仪记录到的地震波是包含了“地震震源效应、地震波的传播路径效应(介质的几何扩散、介质的非弹性衰减)、台站场地响应、仪器响应和噪声”的综合信息,只有扣除了传播路径效应、台站场地响应及仪器响应等,才能得到震源谱。
在台站j的地震仪记录的第i个地震地面运动的傅里叶谱为
| ${A_{ij}}\left( f \right) = {A_{i0}}\left( f \right) \cdot G\left( {{R_{ij}}} \right) \cdot {S_j}\left( f \right) \cdot {I_j}\left( f \right) \cdot {{\rm{e}}^{ - \frac{{{\rm{ \mathit{ π} }}{R_{ij}}f}}{{Q\left( f \right)\beta }}}}$ | (3) |
式中,Aij(f)为在第j个台观测到的第i个地震的傅里叶振幅谱(观测谱);Ai0(f)为第i个地震的震源振幅谱(震源谱);Rij为震源距(第i个地震到第j个台站);G(Rij)为几何衰减函数;Q(f)为频率依赖的品质因子;β为地震波速度(本文仅分析S波);Sj(f)为第j个台站的场地响应项;Ij(f)为第j个台站的仪器响应项;f为频率。
在频率域内,经过对台站观测位移谱Aij(f)几何衰减、非弹性衰减、场地响应及仪器响应校正后,得到了震源谱Ai0(f)。本文采用三段几何衰减模型计算传播路径的影响(Atkinson et al,1992;黄玉龙等,2003),采用多台、多地震联合反演的Moya等(2000)方法计算台站的场地响应,仪器响应可通过仪器标定进行校正。
在计算台站观测震源谱时必须首先对地震记录扣除传播路径效应、台站场地响应及仪器响应等,其中最为关键的是,介质品质因子Q,Q是地球介质的重要物理参数,描述由于介质的非完全弹性,地震波在介质里传播过程中的衰减,或者说能量耗损的特征,其定义为
| $\frac{1}{Q} = \frac{1}{{2{\rm{ \mathit{ π} }}}}\frac{{\Delta E}}{E}$ | (4) |
其中,E为一定体积的地球介质在地震波一个周期T(或一个波长λ)的运动中所积累的能量;ΔE为同一体积的介质在地震波一个周期(或一个波长λ)的运动中所耗损的能量。由式(4)可知,地震波在Q值较大的介质里传播时,耗损的能量较小,波衰减较慢。
采用Brune二次方衰减震源谱模型中的ω2作为理论震源谱Athe0(f),利用遗传算法求解由A0(f)和Athe0(f)定义的残差为极小的震源谱参数Ω0(零频振幅)和拐角频率fc(Brune,1970)。利用得到的震源谱参数求得地震矩M0为
| ${M_0} = \frac{{4{\rm{ \mathit{ π} }}\rho {\beta ^3}{\mathit{\Omega }_0}}}{{2{R_{\theta \varphi }}}}$ | (5) |
其中,密度ρ取2.7g/cm3,β是S波速度,Rθφ是震源的辐射花样系数;求得的应力Δσ为
| $\Delta \sigma = \frac{7}{{16}}\frac{{{M_0}}}{{{r^3}}} = \frac{{\rho {{\left( {2{\rm{ \mathit{ π} }}{f_{\rm{c}}}} \right)}^3}{\mathit{\Omega }_0}}}{{2.34{R_{\theta \varphi }}}}$ | (6) |
式中,密度ρ取2.9g/cm3;β是S波速度(取3.5km/s);r为震源特征尺度;R是辐射花样系数(由于没有每次地震的断层面解,令其为一常数,取S波在震源球上辐射花样系数的平均值为
矩震级MW由地震矩M0计算得到(Kanamori,1977a、1977b;Hanks et al,1979)
| ${M_{\rm{W}}} = \frac{2}{3}\left( {\lg {M_0} - 9.1} \right)$ | (7) |
依据上述原理反演得到182次ML≥2.8地震的震源参数(地震矩、矩震级和应力降),表 1仅给出19次ML≥3.8地震震源参数。
| 表 1 ML≥3.8地震的矩震级目录 |
矩震级是完全由地震矩决定的震级。矩震级原本就是按面波震级不饱和时两者的测定结果应当一致的原则定义的(刘瑞丰等,2015)。矩震级反映了形变规模的大小,是目前度量地震大小最好的物理量,不会产生震级饱和问题。
首先,将测定的近震震级ML和矩震级MW进行了对比分析(图 6),从图 6可看到ML与MW基本呈线性关系。我们研究的地震大多数都在4.5级以下,这些地震的震源基本上都是点源,地震波的优势周期基本为1.0s左右,近震震级ML可以很好地表示地震的大小。而矩震级MW是一个均匀的震级标度,无论是大地震还是小地震,无论是深震还是浅震,矩震级都可以表示地震的大小。

|
图 6 矩震级MW与ML的回归关系 |
采用线性回归方法,对得到182个地震ML与MW进行了回归分析(图 6、表 2)。从图 6可知,近震震级ML的变化范围为2.8~5.0,矩震级MW的变化范围为2.5~4.2,ML与MW呈较好的线性关系,相关系数R=0.9302,表明随着ML的增大,矩震级MW也增大。ML与MW回归关系为
| 表 2 近震震级ML与矩震级MW线性回归关系 |
| ${M_{\rm{W}}} = 0.72{M_{\rm{L}}} + 0.66$ |
分析拟合关系可知,当ML=2.35时,ML和MW相等;当ML<2.35时,ML>MW;当ML>2.35时,ML<MW。
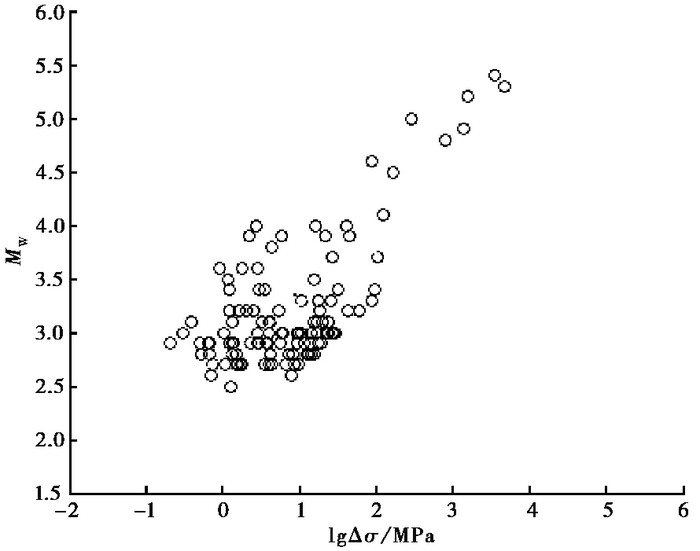
3.4 矩震级和应力降的关系基于线性回归方法,对182个地震的矩震级MW和应力降Δσ进行回归分析(图 7)。从图 7可知,MW和lgΔσ呈弱正相关,基本上是lgΔσ随着MW增加而增加。当MW<2.5时,线性关系不明显;MW>2.5时,线性关系较显著。矩震级的分布范围为2.5~5.4,lgΔσ分布范围为10-1~104,且优势分布范围在1~102,显示出MW对lgΔσ有弱的依赖性。
|
图 7 矩震级MW与应力降lgΔσ的回归关系 |
通过对内蒙古中西部地区中小地震矩震级的研究认为,将描述震源物理性质的矩张量解纳入地震目录的快报和正式报告中,不仅可以避免震级饱和问题,也可以和国际地震资料接轨。同时,丰富了地震观测报告内容,更好地为地震应急和地震科研服务。
(1) 矩震级是一个均匀的震级标度,适于震级范围很宽的统计,不会出现震级饱和现象,无论是对大震还是小震、微震,甚至极微震,无论是对浅震还是深震,均可测量。研究认为,在一定震级范围内,矩震级能与常规的面波震级衔接起来,在区域测震台网常规测定中小地震的矩震级是可行的。
(2) 近震震级ML与矩震级MW呈较好正相关关系,随着ML的增大,矩震级MW也增大。ML与MW回归关系式为MW=0.72ML+0.66。
(3) 矩震级MW和应力降对数lgΔσ的线性相关性较弱,MW对lgΔσ依赖性较弱。
(4) 鉴于本文所研究的时段,内蒙古中西部地区发生ML≥2.8的地震数量不多,且地震分布不够均匀,所建立的近震震级与矩震级、矩震级和应力降间的关系还有待在今后的使用过程中不断完善,使其更符合内蒙古地区静力学参数定标关系。
| 曹刚. 2001, 内蒙古地震研究. 北京: 地震出版社. |
| 陈运泰, 刘瑞丰. 2004, 地震的震级. 地震地磁观测与研究, 25(6): 1–12. |
| 陈运泰, 吴忠良, 王培德, 等. 2000, 数字地震学. 北京: 地震出版社. |
| 高景春, 赵英萍, 等. 2011, 河北省测震台网中小地震矩震级的测定. 华北地震科学, 29(2): 1–4. |
| 金春华, 李鸿庭, 盛菊琴. 2012, 宁夏及邻区地震动衰减和场地响应的分区研究. 地震地磁观测与研究, 33(5/6): 24–29. |
| 康英, 杨选, 沈玉松. 2015, 传统地震目录中增加矩震级及震源机制解的必要性分析. 中国地震, 31(1): 121–132. |
| 刘瑞丰, 陈运泰, 任枭, 等. 2015, 震级的测定. 北京: 地震出版社. |
| 刘芳, 朱智勇. 2007, 内蒙古中西部地区的中小地震震源参数. 华北地震科学, 25(2): 10–14. |
| 刘丽芳, 苏有锦, 等. 2010, 云南和四川中小地震应力降时空特征研究. 地震研究, 33(3): 314–319. |
| 孙加林, 杨毅, 曹井泉. 1998, 1996年包头西6.4级地震震兆特征的特殊性. 地震, 18(3): 233–239. |
| 王鑫, 张帆, 尹战军, 等. 2015, 内蒙古数字测震台网单台近震震级偏差研究. 地震地磁观测与研究, 36(6): 26–32. |
| 杨晶琼, 杨周胜, 等. 2010, 2008年盈江5.9级地震序列震源参数研究. 地震研究, 33(4): 309–310. |
| 杨晶琼, 刘丽芳, 杨周胜. 2013, 云南中小地震矩震级的测定. 地震研究, 36(3): 306–312. |
| 中华人民共和国国家标准《地震震级的规定》(GB17740-2017). |
| Atkinson G M, Mereu R F. 1992, The shape of ground motion attenuation curves in southeastern Canada. Bull Seism Soc Am, 82: 2014–2031. |
| Brune J N. 1970, Tectonic stress and the spectra of seismic shear waves from earthquake. J Geophys Res, 75(26): 4997–5009. DOI:10.1029/JB075i026p04997. |
| Dziewonski A M, Chou T A, Woodhouse J H. 1981, Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J Geophys Res, 86: 2825–2852. DOI:10.1029/JB086iB04p02825. |
| Dziewonski A M, Woodhouse J H. 1983, An experiment in systematic study of global seismicity:Centroid-moment tensor solutions for 201 moderate and large earthquakes of 1981. J Geophys Res, 88: 3247–3271. DOI:10.1029/JB088iB04p03247. |
| hanks T C, Kanamori H A. 1979, Moment magnitude scale. J Geophys Res, 84(B5): 2348–2350. DOI:10.1029/JB084iB05p02348. |
| Kanamori H. 1977a, The energy release in great earthquakes. J Geophys Res, 82: 2981–2987. DOI:10.1029/JB082i020p02981. |
| Kanamori H. 1977b, The energe release in great earthquakes. J Geophys Res, 82(20): 2981–2987. DOI:10.1029/JB082i020p02981. |
| Moya C A, Aguirre J, Irikura K. 2000, Inversion of source parameters and site effects from strong ground motion records using genetic algorithms. Bull Seism Soc Amer, 90(4): 977–992. DOI:10.1785/0119990007. |
| Sipkin S A. 1982, Estimation of earthquake source parameters by the inversion of waveform data:Synthetic waveforms. Phys Earth Planet Inter, 30: 242–259. DOI:10.1016/0031-9201(82)90111-X. |
 2017, Vol. 33
2017, Vol. 33


