地震层析成像从医学CT引入地球物理学领域用于地壳上地幔速度结构研究(Aki et al,1976)以来,已发展成为研究地球内部速度结构(白志明等,2016)最重要的方法之一。利用地震层析成像得到地球内部高分辨率的速度结构模型,为探索全球构造进程,岩石圈的演化和构造运动,全球板块运动的规律和动力机制,以及地震、火山活动发生的深部构造环境等提供了十分重要的科学依据(Zhao,2001;田有等,2009)。地震层析成像技术根据所使用的地震波、资料类型的不同,可分为体波层析成像(Aki et al,1977;Zhao,2004)和面波层析成像(Shapiro et al,2005);根据研究区域尺度大小的不同,可分为全球层析成像和区域层析成像。由于面波本身的长波长性质,面波层析成像主要用于全球范围或大尺度区域的研究;而体波波长较短,具有较高的空间分辨率,因此,体波层析成像可用于局部区域的研究(Zhao,2001)。目前,应用较多的依然是体波(P波)的走时层析成像,其所反演的参数也由单纯的介质速度结构发展到介质速度结构和震源位置,或者同时反演介质速度结构和界面深度(Aki et al,1976、1977;Pavlis et al,1980;刘福田,1984;Bishop et al,1985;Zhao et al,1992;Zelt et al,1992;华标龙等,1995;Rawlinson et al,2001;周龙泉等,2006)。Zhao(2001)、Rawlinson等(2010)分别对地震层析成像技术进行了系统的总结。
地震走时层析成像是建立在一定的模型参数化和正演射线追踪基础之上的。在对地球介质进行模型参数化时,根据其空间分布特征可分为离散介质和连续介质2种类型。对于离散介质类型一般将地球介质进行网格划分,常见的为大小相等的矩形网格(三维为立方体),在网格内部或节点上定义各自的地震波速度等属性。网格结构存在2个主要困难:一是难于描述复杂构造的精细结构;二是为了满足描述最精细区域的要求,网格结构通常需要密度较大的网格节点,而网格节点上的正演计算通常至少与网格节点数目成正比(Moser,1991),因此,受计算机内存和运算速度的影响很大,对于三维空间尤其如此。而离散化模型适应性强,在此基础上的走时计算和射线追踪方法健壮性好是其最大的优点。
层状结构是常见的分段连续介质描述方法,其以不同的分层界面来描述物性间断面。层状结构描述简单,模型基础上的正演射线追踪计算方便快捷(Zelt et al,1992;Zhang et al,2007、2013)。但层状结构在描述逆断层等复杂三维地质体时会变得十分困难,而块状结构描述则容易的多。块状结构模型中,三维地质体被看做不同地质块组成的集合体。Gjøystdal等(1985)首先提出了三维块状建模的概念,地质块采用集合运算的操作来构造,显示很不直观。Pereyra(1996)发展了块状模型描述的技术,块体更加直观自然,但模型界面采用B样条曲面描述,这使其受到限制,只能构造尖灭和蘑菇云等典型地质模型。我们在此基础上采用三角形面片描述模型界面,在构建复杂模型方面有了很大的提升,理论上可以构建任意复杂构造的地质体(徐涛等,2004;Xu et al,2006、2008、2010;李飞等,2013)。
传统的运动学射线追踪方法包括试射法(Langan et al,1985;Sun,1993;Sambridge et al,1995;徐涛等,2004)和弯曲法(Julian et al,1977;Thurber et al,1980;Um et al,1987;Xu et al,2006、2010、2014;李飞等,2013;Li et al,2014)。试射法在全局搜索接收器方面效果较好,而弯曲法的计算效率较高。Ceverny(2001)对射线追踪方法进行了很好的总结。在前期的工作中,基于块状建模方法我们已经发展了适用于常速度(Xu et al,2006)、常梯度速度分布(Xu et al,2010)的逐段迭代射线追踪算法,以及VTI介质中的子三角形法射线追踪算法(Xu et al,2008)。之后,我们将块状模型介质扩展到任意速度分布的非均匀介质,发展了与之相适应的逐段迭代射线追踪算法,并结合伪弯曲法提出了射线追踪的3点修正方案(李飞等,2013)。三维模型实验显示了该射线追踪扰动修正方案的适用性,相对于试射法,其追踪效率显著提高。本文基于三维块状建模以及快速高效的逐段迭代射线追踪,采用模拟退火非线性反演算法,开展了三维速度模型中的地震波走时反演研究。
1 模型参数化及正演射线追踪 1.1 三维非均匀块状模型块状结构模型中,地质体被看作由大小不等、形状各异的地质块组成的集合体,每个地质块有各自的地质属性,如地震波速度、密度等物性结构,并与其他的地质块存在相邻的边界(徐涛等,2004;Xu et al,2006)。我们对二维区域剖面采用“域-面—边-点”的描述方式(徐果明等,2001;Xu et al,2010)。不同的地质面元为封闭的,被边界分隔开,边界由离散点插值得到的3次样条给定。三维地质体的描述采用“体-块—面-三角形-点”的层次结构(徐涛等,2004;Xu et al,2006、2008、2010;李飞等,2013)。不同地质块之间的物性分界面由一系列的三角形面片拼接而成。
三维块状模型中界面的描述极为关键。与Coons、Bezier、B样条等曲面相比,三角形面片有诸多优势(李飞等,2013)。在三维建模软件GOCAD系统中,也是利用三角形来构造模型界面的(Mallet,1989)。三角形内部各点法向量是确定且唯一的,如果2个三角形面片不在1个平面上,则界面法向量在跨三角形的连接处会出现突变,因此,会造成反射、透射射线在跨连接处也会出现突变,这对于如扰动量修正射线轨迹的弯曲法射线追踪存在极大的困难。针对该问题,我们对界面上各点的法向量进行了光滑处理,重新定义界面上各点的法向量,使得法向量在整个界面内连续变化(徐涛等,2004;Xu et al,2006、2008、2010;李飞等,2013)。
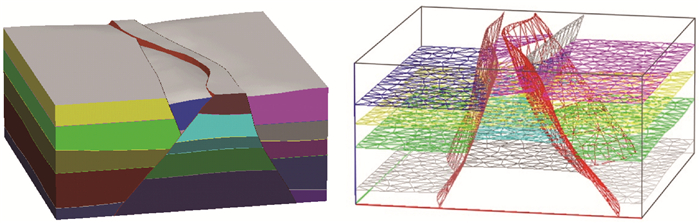
图 1为我们采用块状建模并结合三角形界面描述方式设计的一个典型三维模型,该模型比类伸展盆地中的堑垒构造,该构造广泛存在于中国东部如渤海湾盆地、苏北盆地以及松辽盆地等。模型由18个地质块构成,6676个三角形描述模型界面,三角形则由2700个离散点控制。
|
图 1 复杂堑垒构造地质体 不同颜色代表不同的地质块(左);模型界面由三角形面片构成(右) |
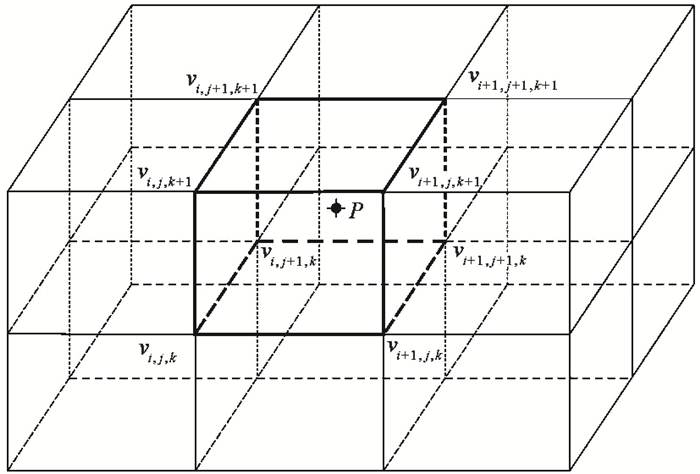
为了描述三维模型中非均匀的速度分布,我们对三维地质体每个块体内部速度场单独定义,分别建立1套独立的矩形网格节点,并在节点上定义速度值(图 2)。如图 2所示,对于某块体内部的任意点P(x,y,z),首先找到该点在矩形网格中的位置,再由周围8个节点位置处的速度三线性插值获得P点的速度v(x,y,z)。
|
图 2 由矩形网格定义的非均匀速度场 |
| $ \begin{array}{l} v\left( {x,y,z} \right) = \Sigma _{l = 0}^1\Sigma _{m = 0}^1\Sigma _{n = 0}^1v\left( {i + l,j + m,k + n} \right)\\ \left( {1 - \left| {\frac{{x - {x_{i + l}}}}{{{x_{i + 1}} - {x_i}}}} \right|} \right)\left( {1 - \left| {\frac{{y - {y_{j + m}}}}{{{y_{j + 1}} - {y_j}}}} \right|} \right)\left( {1 - \left| {\frac{{z - {z_{k + n}}}}{{{z_{k + 1}} - {z_k}}}} \right|} \right) \end{array} $ | (1) |
式中,v(i+l, j+m, k+n)分别为8个节点的速度值;xi,yj,zk分别为矩形速度网格在x,y,z方向的位置坐标。
综上所述,我们在三维块体内部定义一系列立方体速度网格,网格内部任意位置处速度由其所在速度网格顶点位置处的速度通过线性插值获得,通过网格顶点速度值控制整个模型的速度分布。由此,三维块体内部可以定义为常速度、常梯度速度、任意非均匀速度等分布。相邻块体之间的分界面由一系列的三角形面片拼接而成,三角形顶点位置可以随意改变,通过三角形顶点位置的抬升与下降来控制模型界面的起伏。
1.2 三维非均匀块状模型的射线追踪Um等(1987)提出了伪弯曲法射线追踪用于解决连续介质中的2点射线追踪问题,但却无法适应存在强速度间断面的情况。我们提出了逐段迭代射线追踪算法,用于追踪存在强速度间断面模型,该算法属于弯曲法的范畴,已经在二维、三维常速度分布(Xu et al,2006)和常梯度速度分布(Xu et al,2010)中均取得了很好的射线追踪效果。对于更普遍的非均匀介质模型,我们发展了相适应的逐段迭代射线追踪算法(李飞等,2013)。下面简述逐段迭代法修正界面路径点的基本原理。
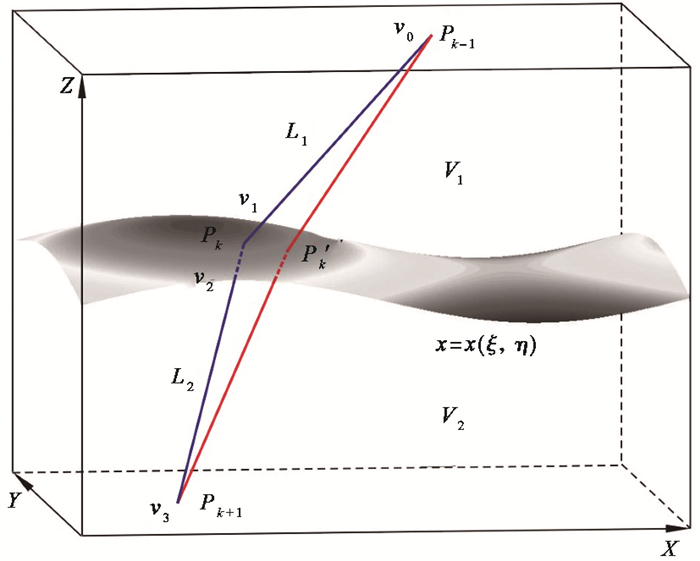
图 3为逐段迭代法修正中间点示意图。如图 3所示,对于任意分布的非均匀介质,假设Pk-1、Pk+1为跨过界面的射线路径的起始点和终止点;Pk为落在界面上的路径点,满足界面方程
| $ {\mathit{\boldsymbol{x}}_k} = {\mathit{\boldsymbol{x}}_k}\left( {\xi ,\eta } \right) $ | (2) |
|
图 3 逐段迭代法修正中间点示意图 |
如果Pk-1、Pk+1与Pk点间的距离很小,则射线轨迹可近似看作2个直线段Pk-1Pk和PkPk+1。固定起始点Pk-1和终止点Pk+1,则射线轨迹的走时T是中间点Pk坐标xk(ξ, η)的函数
| $ T = {t_1}({P_{k - 1}},{\mathit{\boldsymbol{x}}_k}) + {t_2}({\mathit{\boldsymbol{x}}_k},{P_{k + 1}}) $ | (3) |
式(3)可近似写为
| $ T = \left| {{\mathit{\boldsymbol{x}}_k} - {\rm{ }}{\mathit{\boldsymbol{x}}_{k - 1}}} \right|(1/{v_0} + 1/{v_1})/2 + \left| {{\mathit{\boldsymbol{x}}_{k + 1}} - {\rm{ }}{\mathit{\boldsymbol{x}}_k}} \right|(1/{v_2} + 1/{v_3})/2 $ | (4) |
其中,v0、v3为起始点Pk-1和终止点Pk+1处的速度;v1、v2为界面路径点Pk两侧的速度。
基于射线走时的费马原理,假设修正后的路径点位置为(ξ+Δξ, η+Δη),则有如下的偏导数方程成立
| $ {\left. {\frac{{\partial T}}{{\partial \xi }}} \right|_{(\xi = \xi + \Delta \xi ,\eta = \eta + \Delta \eta )}} = 0,\;\;\;\;{\left. {\frac{{\partial T}}{{\partial \eta }}} \right|_{(\xi = \xi + \Delta \xi ,\eta = \eta + \Delta \eta )}} = 0 $ | (5) |
对式(5)进行泰勒展开,并保留一阶小量,最终可计算得到中间点的一阶修正量(Δξ, Δη),详细公式推导过程可参见文献(李飞等,2013)。
针对存在速度间断面的非均匀介质,我们联合伪弯曲法和逐段迭代法,提出了1种扰动修正方案:对于落在界面上,即速度间断面上的路径点,进行逐段迭代法的扰动修正;而对于在模型连续介质内部的路径点,用伪弯曲法来修正,这样可适应三维复杂非均匀介质且存在速度间断面的情况(李飞等,2013)。与Zhao等(1992)的射线追踪过程相比,我们在逐段迭代过程中采用一阶显式修正的方式,而不是迭代的方法修正落在界面上的路径点,因此,追踪过程更高效省时。
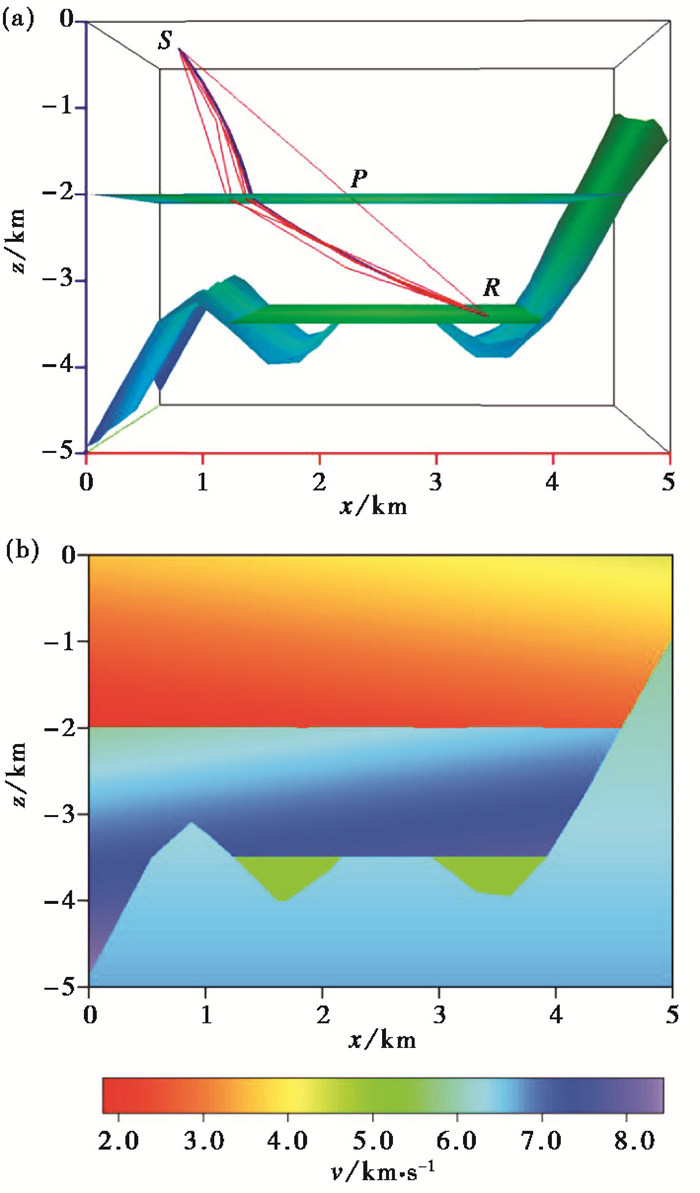
图 4为我们设计的一个地层互切模型的射线追踪结果,模型在x、y、z轴3个方向的尺度均为5km,定义z轴向上为正。地层互切模型(图 4(a))包含5个地质块、3635个三角形及1681个点。模型的x、y、z轴方向分别以红、绿、蓝3种颜色直线表示(图 4(a))。由图 4(a)可见,直线连接起始点S、终止点R以及与模型界面的交点P,作为初始射线路径,图中显示了追踪过程中的部分射线路径变化及最终的射线追踪结果。图 4(b)显示了三维非均匀速度场在y=2.5km处的速度切片。
|
图 4 地层互切模型的射线追踪结果 (a)射线路径的3点修正过程示意图,蓝线为最终路径;(b)y=2.5km处速度切片 |
综上所述,我们采用块状建模并结合三角形界面可以构建任意复杂的三维地质体,同时发展了适应于非均匀速度分布且存在速度间断面的逐段迭代法,并结合伪弯曲法,提出了复杂块状模型中射线追踪的3点修正方案,该方案具有很强的适应性,且相对于试射法追踪效率显著提高,这为地震体波走时反演研究打下了坚实的基础。
2 模拟退火非线性反演算法地球物理反演理论自诞生至今,已取得了长足的进展,形成了一系列较为成熟的线性、非线性反演算法,如最小二乘(Miller,2006)、共轭梯度法(Fletcher et al,1964)、模拟退火(Bertsimas et al,1993)、遗传算法等。本文采用模拟退火非线性反演算法,进行了三维速度模型的地震波走时反演研究。
模拟退火法(Bertsimas et al,1993)是一种用于求解大规模优化问题的随机搜索算法。它以优化问题求解过程与物理系统退火过程之间的相似性为基础;优化的目标函数相当于金属的内能;优化问题的自变量组合相当于金属的内能状态空间;问题的求解过程就是寻找一个组合状态,以使得目标函数值最小。该方法利用Metropolis准则并适当地控制温度的下降过程实现模拟退火,从而达到在多项式时间内求解全局优化问题的目标。
模拟退火算法来源于固体退火原理,将固体加温至温度充分高,再让其徐徐冷却,加温时,固体内部粒子随温度升高变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。用固体退火模拟组合优化问题,将内能E模拟为目标函数值f,温度T演化成控制参数t,即得到解组合优化问题的模拟退火算法。退火过程由冷却进度表控制,包括控制参数的初值T0及其衰减因子ΔT,每个T值时的迭代次数L和停止条件S。模拟退火算法的基本流程如下:
(1) 随机产生1个初始解x0,令xbest=x0,并计算目标函数值E(x0)。
(2) 设置初始温度T(0)=T0,迭代次数i=1。
(3) Do while T(i)>Tmin,其中,Tmin为设定的最低温度
1) for j=1~k;
2) 对当前最优解xbest按照某一邻域函数产生1个新的解xnew,并计算新的目标函数值E(xnew),目标函数值的增量ΔE=E(xnew)-E(xbest);
3) 如果ΔE < 0,则xbest=xnew;
4) 如果ΔE>0,则计算状态转移概率P=exp(-ΔE/T(i)),随机产生1个0~1之间的随机数c=random[0,1],如果c < P,则xbest=xnew,否则xbest=xbest;
5) End for。
(4) Ti+1=Ti-ΔT,i=i+1。
(5) End do。
(6) 输出当前最优点,计算过程结束。
状态转移概率是指从一个状态xold (一个可行解)向另一个状态xnew (另一个可行解)的转移概率,可以通俗地理解为接受一个新解为当前解的概率,它与当前的稳定参数T有关,并随温度下降而减小,一般采用Metropolis准则
| $ P = \left\{ {\begin{array}{*{20}{l}} 1&{{\rm{if}}\;\;E({x_{{\rm{new}}}}) < E\left( {{x_{{\rm{old}}}}} \right)}\\ {{\rm{exp}}\left[ { - \frac{{E\left( {{x_{{\rm{new}}}}} \right) - E\left( {{x_{{\rm{old}}}}} \right)}}{T}} \right]}&{{\rm{if}}\;\;E\left( {{x_{{\rm{new}}}}} \right) \ge E\left( {{x_{{\rm{old}}}}} \right)} \end{array}} \right. $ | (6) |
模拟退火过程中的冷却进度表是指从某一个高温状态T0向低温状态冷却时的降温管理表,时刻t的温度用T(t)表示。经典模拟退火算法的降温方式为
可以通过增加某些环节以实现对模拟退火算法的改进,主要的改进方式包括:在算法进程中的适当时机,增加升温和重升温过程,将温度适当提高,可激活各状态的接受概率,进而调整搜索进程中的当前状态,避免算法在局部极小解处停滞不前;为避免搜索过程中由于执行概率接受环节而遗失当前遇到的最优解,可通过增加存储环节,将当前遇到的最优解记忆下来;在退火过程结束后,以搜索到的最优解为初始解,再次执行模拟退火过程或者局部性搜索,即增加补充搜索过程;还可以结合其他搜索机制的算法,如遗传算法等。
3 模型实验运用模拟退火算法,我们进行了层状介质中均匀速度反演的模型实验,理论模型采用图 5所示的简单层状模型。理论模型中第1、2两层介质速度分别为4.8、5.4km/s,2层界面深度分别为-1.35、-2.4km,第2层介质底界面为地震波反射界面。建立如图 5所示的单炮记录观测系统,接收器均匀排列于地表。初始模型中固定界面深度值为理论值,且保持不变,介质速度初始值在真实值附近某一邻域范围内随机产生。
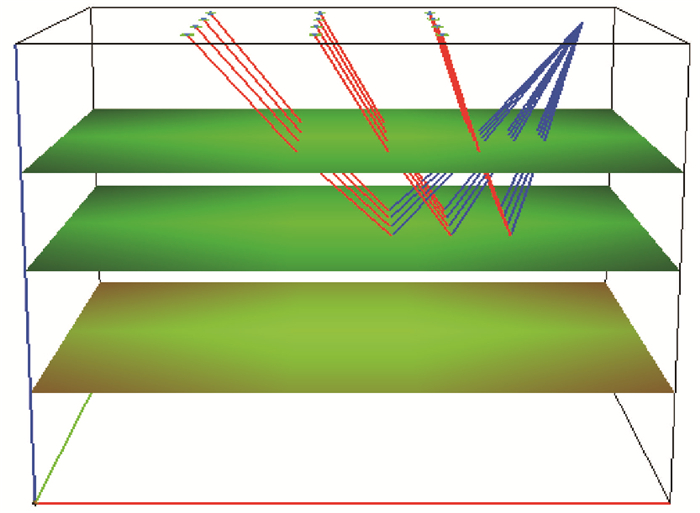
|
图 5 水平层状均匀介质理论模型及射线追踪结果示意图 |
模拟退火算法的目标函数设为
| $ \varphi = \sum\limits_{i = 1}^n {\frac{1}{n}\left| {{T_{{\rm{obs}}}} - {T_{{\rm{cal}}}}} \right|} $ | (7) |
优化的目标即为寻找1组速度值,以使得目标函数值最小。设定退火初始温度为T0=10000,初始温度越大,则获得高质量解的概率越大。
降温方式采用指数衰减形式
| $ T\left( k \right) = {T_0}{{\rm{e}}^{ - \beta k}} $ | (8) |
其中,β为给定的温度衰减常数,如β=0.2;k为外层循环次数。
降温过程中,在某一确定的温度状态T(k)下,对当前最优速度解按照某一邻域函数产生1组新的解进行,并重新计算目标函数。在迭代进程中根据需要可适当缩小邻域的步长。
实际反演过程中采用的模型速度更新方式为
| $ {v_1}\prime = {v_1} + \frac{{100\xi }}{{k + 1}} $ | (9) |
| $ {v_2}\prime = {v_2} + \frac{{100\xi }}{{k + 1}} $ | (10) |
其中,ξ为[-1,1]之间的随机数;k的定义同式(8)。
在迭代进程中,如果搜索到的最优值连续若干步保持不变,则认为迭代终止,此时获得的速度参数即为通过模拟退火非线性反演算法获得的最优解。采用模拟退火非线性反演算法进行的水平层状均匀模型介质速度反演结果如图 6所示,其中,2层介质速度真实值分别为v1=4.8km/s,v2=5.4km/s。
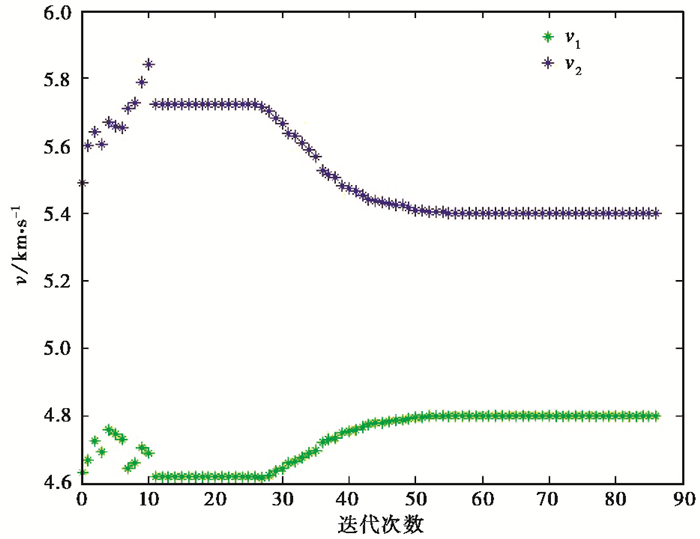
|
图 6 模拟退火速度反演结果随迭代次数的变化 |
块状结构结合三角形界面可描述复杂的三维模型,在很大程度上克服了层状结构描述复杂模型的困难。正演过程中采用的逐段迭代射线追踪方法可适应三维复杂非均匀介质的块状模型。模拟退火非线性反演算法实现了三维速度模型中的地震波走时反演。模型测试结果表明了反演工作的高效性,下一步将进一步考虑三维复杂模型中速度与界面的联合反演。
| 白志明, 吴庆举, 徐涛, 等. 2016, 中国大陆下扬子及邻区地壳结构基本特征:深地震测深研究综述. 中国地震, 32(2): 180–192. |
| 华标龙, 刘福田. 1995, 界面和速度反射联合成像——理论与方法. 地球物理学报, 38(6): 750–756. |
| 李飞, 徐涛, 武振波, 等. 2013, 三维非均匀地质模型中的逐段迭代射线追踪. 地球物理学报, 56(10): 3514–3522. DOI:10.6038/cjg20131026 |
| 刘福田. 1984, 震源位置和速度结构的联合反演(Ⅰ)——理论和方法. 地球物理学报, 27(2): 167–175. |
| 田有, 赵大鹏, 刘财, 等. 2009, 体波走时层析成像方法及其在中国壳幔结构研究中的应用评述. 地学前缘, 16(2): 347–360. |
| 徐果明, 卫山, 高尔根, 等. 2001, 二维复杂介质的块状建模及射线追踪. 石油地球物理勘探, 36(2): 213–219. |
| 徐涛, 徐果明, 高尔根, 等. 2004, 三维复杂介质的块状建模和试射射线追踪. 地球物理学报, 47(6): 1118–1126. |
| 周龙泉, 刘福田, 陈晓非. 2006, 三维介质中速度结构和界面的联合成像. 地球物理学报, 49(4): 1062–1067. |
| Aki K, Christoffersson A, Husebye E S. 1977, Determination of the three-dimensional seismic structure of the lithosphere. J Geophys Res, 82: 277–296. DOI:10.1029/JB082i002p00277. |
| Aki K, Lee W H K. 1976, Determination of three dimensional velocity anomalies under a seismic array using first P arrival times from local earthquakes. J Geophys Res, 81: 4381–4399. DOI:10.1029/JB081i023p04381. |
| Bertsimas D, Tsitsiklis J. 1993, Simulated Annealing. Statistical Science, 8(1): 10–15. DOI:10.1214/ss/1177011077. |
| Bishop T N, Bube K P, Cutler R T, et al. 1985, Tomography determination of the velocity and depth in laterally varying media. Geophysics, 50: 903–923. DOI:10.1190/1.1441970. |
| Cerveny V. 2001, Seismic ray theory. Oxford: Cambridge University Press |
| Fletcher R, Reeves C M. 1964, Function minimization by conjugate gradients. The Computer Journal, 7(2): 149–154. DOI:10.1093/comjnl/7.2.149. |
| Gjøystdal H, Reinhardsen J E, Åstebol K. 1985, Computer representation of complex 3-D geological structures using a new "solid modeling" technique. Geophys Prospect, 33: 195–211. |
| Julian B R, Gubbins D. 1977, Three-dimensional seismic ray tracing. J Geophys, 43: 95–113. |
| Langan R T, Lerche I, Culter R T. 1985, Tracing of rays through heterogenous media:An accurate and efficient procedure. Geophysics, 50: 1456–1465. DOI:10.1190/1.1442013. |
| Li F, Xu T, Zhang M, et al. 2014, Seismic traveltime inversion of 3D velocity model with triangulated interfaces. Earthquake Science, 27(2): 127–136. DOI:10.1007/s11589-013-0025-0. |
| Mallet J L. 1989, Discrete smooth interpolation. ACM Transactions on Graphics, 8: 121–144. DOI:10.1145/62054.62057. |
| Miller S J, 2006, The method of least squares, 1~7, Williamstown: Department of Mathematics and Statistics, Williams College. |
| Moser T J. 1991, Shortest path calculation of seismic rays. Geophysics, 56: 59–67. DOI:10.1190/1.1442958. |
| Pavlis L G, Booker J R. 1980, The mixed discrete-continuous inverse problem:application to the simultaneous determination of earthquake hypocenters and velocity structure. J Geophys Res, 85: 4801–4810. DOI:10.1029/JB085iB09p04801. |
| Pereyra. 1996, Modeling, ray tracing, and block nonlinear travel-time inversion in 3-D. Pure Appl Geophys, 148: 345–386. DOI:10.1007/BF00874572. |
| Rawlinson N G, Houseman A, Collins C D N. 2001, Inversion of seismic refraction and wide-angle reflection traveltimes for three-dimensional layered crustal structure. Geophys J Int, 145: 381–400. DOI:10.1046/j.1365-246x.2001.01383.x. |
| Rawlinson N, Pozgay S, Fishwick S. 2010, Seismic tomography:A window into deep Earth. Phys Earth Planet Inter, 178: 101–135. DOI:10.1016/j.pepi.2009.10.002. |
| Sambridge M, Braun J, McQueen H. 1995, Geophysical parameterization and interpolation of irregular data using natural neighbors. Geophys J Int, 122: 837–857. DOI:10.1111/gji.1995.122.issue-3. |
| Shapiro N M, Campillo M, Stehly L, et al. 2005, High-resolution surface-wave tomography from ambient seismic noise. Science, 307: 1615–1618. DOI:10.1126/science.1108339. |
| Sun Y. 1993, Ray tracing in 3-D media by parameterized shooting. Geophys J Int, 114: 145–155. DOI:10.1111/gji.1993.114.issue-1. |
| Thurber C, Ellsworth W. 1980, Rapid solution of ray tracing problems in heterogeneous media. Bull Seism Soc Am, 70: 1137–1148. |
| Um J, Thurber C. 1987, A fast algorithm for two-point seismic ray tracing. Bull Seism Soc Am, 77: 972–986. |
| Xu T, Li F, Wu Z, et al. 2014, A successive three-point perturbation method for fast ray tracing in complex 2D and 3D geological models. Tectonophysics, 627: 72–81. DOI:10.1016/j.tecto.2014.02.012. |
| Xu T, Xu G M, Gao E G, et al. 2006, Block modeling and segmentally iterative ray tracing in complex 3D media. Geophysics, 71: T41–T45. DOI:10.1190/1.2192948. |
| Xu T, Zhang Z J, Gao E G, et al. 2010, Segmentally iterative ray tracing in complex 2D and 3D heterogeneous block models. Bull Seism Soc Am, 100(2): 841–850. DOI:10.1785/0120090155. |
| Xu T, Zhang Z, Zhao A, et al. 2008, Sub-triangle shooting ray tracing in complex 3D VTI media. Journal of Seismic Exploration, 17: 131–144. |
| Zelt C A, Smith R B. 1992, Seimic traveltime inversion for 2-D crustal velocity structure. Geophys J Int, 108: 16–4. DOI:10.1111/gji.1992.108.issue-1. |
| Zhang Z J, Xu T, Zhao B, et al. 2013, Systematic variations in seismic velocity and reflection in the crust of Cathaysia:New constraints on intraplate orogeny in the South China continent. Gondwana Res, 24(3-4): 902–917. DOI:10.1016/j.gr.2012.05.018. |
| Zhang Z, Wang Y. 2007, Crustal structure and contact relationship revealed from deep seismic sounding data in South China. Phys Earth Planet Inter, 165: 114–26. DOI:10.1016/j.pepi.2007.08.005. |
| Zhao D. 2001, New advances of seismic tomography and its applications to subduction zones and earthquake fault zones:A review. the Island Arc, 10: 68–84. DOI:10.1046/j.1440-1738.2001.00291.x. |
| Zhao D. 2004, Global tomographic images of mantle plumes and subducting slabs:insight into deep Earth dynamics. Phys Earth Planet Inter, 146: 3–34. DOI:10.1016/j.pepi.2003.07.032. |
| Zhao D, Hasegawa A, Horiuchi S. 1992, Tomographic imaging of P and S wave velocity structure beneath northeastern Japan. J Geophys Res, 97: 19909–19928. DOI:10.1029/92JB00603. |
 2017, Vol. 33
2017, Vol. 33


