内蒙古自治区地震局, 呼和浩特市哲里木路80号 010051
收稿日期:2015-12-29; 修定日期:2016-02-01
项目类别:中国地震局地震科技星火项目(XH15008)和内蒙古自治区科技重大专项《重点地区地震预测预警技术研究开发与推广示范》》共同资助
作者简介:刘芳, 女, 1963年生, 高级工程师, 主要从事地震监测、地震预报和地震学的研究工作。E-mail:
lfnm88@163.com
On conversion relationship between near earthquake magnitude and the wave magnitude in Inner Mongolia
Earthquake Administration of Inner Mongolia Autonomous, Hohhot 050051, China
0 引言
地震监测是地震预测研究最重要的观测基础,其中,震级是地震预测及其它相关地震研究的一个重要参数(陈运泰等,2000、2004;刘瑞丰,2003)。无论是现行的地震预测方法,还是前兆方面的经验公式,都直接与震级相关。地震研究工作中常使用面波震级MS和近震震级ML两种标度(张宏志等,2007;汪素云等,2010)。自20世纪以来,国内普遍采用的是1971年郭履灿得到的适用于中国华北地区的经验关系式MS,经验=1.13ML-1.08(震中距Δ≤1000km时) ①。目前,区域地震台网大震速报、地震预测预报以及相关地球科学研究中使用的震级M均是由该经验公式转换得到的。由于不同震级的的测量方法不同,因此,在地震台网的震级测定中,不同的震级之间一律不进行换算(刘瑞丰等,2006)。然而,多年的实际工作表明,近震震级ML和面波震级MS的实测结果显示,这2种标度转换关系已不符合目前使用的经验公式,存在系统偏差,需要被校正。
① 郭履灿,1971,华北地区的地方性震级ML和面波震级MS经验关系,全国地震工作会议资料,1~10。
1范数线性回归和2范数正交回归方法是目前最常用的效果较好的获得近震震级ML与面波震级MS间转换关系的方法。从理论上讲,利用正交回归方法研究各种震级标度之间的关系应当更能接近实际测定的震级(Madansky,1959;Fuller,1987;Carroll et al,1996;刘瑞丰等,2007)。国内许多研究者针对不同地区的近震震级ML与面波震级MS间的转换关系采用线性回归和正交回归方法进行了研究,并得到了较好的结果。刘瑞丰等(2006、2007)开展了对中国地震台网与美国地震台网测定震级间的对比研究以及对中国地震台网震级的研究;任克新等(2008)对IASPEI新震级标度与传统震级标度进行了对比分析;谢卓娟等(2012)对中国大陆及邻区面波震级与近震震级之间的经验关系进行了研究;刘国华等(2006)、杨晶琼等(2013)对云南地区,张诚(1981)对甘肃地区近震震级与面波震级之间的转换关系进行了研究。
内蒙古自治区横跨东北、华北与西北地区,且位于南北地震带北段等重要构造区的最北端,地质构造复杂,地震活动较为强烈(曹刚,2001)。多年的近震震级实测工作显示,2种震级标度间的系统偏差给地震学研究者带来了极大的困惑。随着2017年版《地震震级的规定》(GB17740-2017)(刘瑞丰等,2017)的颁布,研究者还将面临近震震级ML与宽频带面波震级MB(BB)(ML≥4.5的速报震级)间的转换关系问题。本文在遵循震级测定“继承性”的原则的基础上,以达到新、旧震级标度的“无缝”衔接为目标,依据新震级标度,基于1范数线性回归和2范数正交回归方法,利用2008~2015年11月以来发生的116次ML≥3.8地震的数字波形资料,在测定近震震级ML、面波震级MS的基础上,增测宽频带面波震级MS(BB),以获得近震震级与面波震级、近震震级与宽频带面波震级间的转换关系,并与郭履灿获得的经验关系①进行对比分析,以期提高内蒙古地震台网震级测定精度,为内蒙古地区的地震预测预报及地震学相关研究提供数据基础。
1 资料的选取
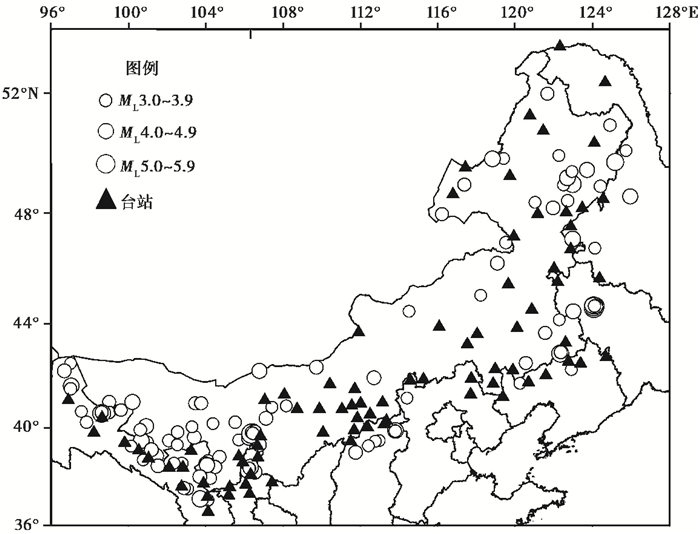
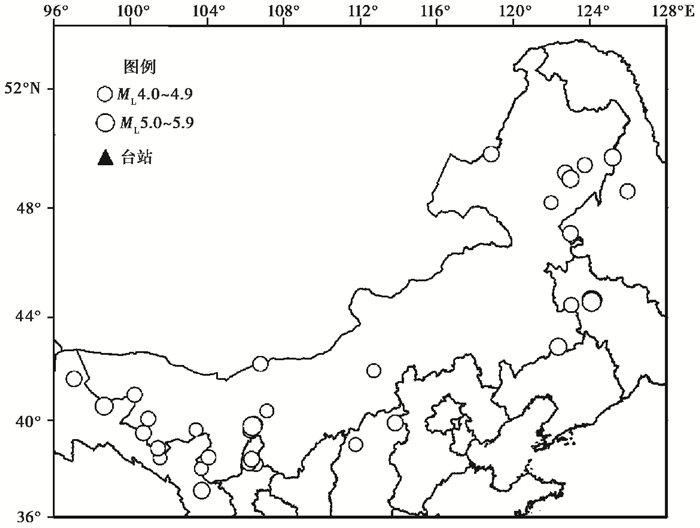
内蒙古“十五”数字化观测网络项目建成以来,由81个数字台站(区内39个、邻省42个)组成的数字化监测网络覆盖了内蒙古大部分地区,监测水平有了大幅度提高,这为校正内蒙古近震震级与面波震级、新建近震震级与宽频带面波震级间的转换关系提供了必要的数据基础。本文选取116次ML≥3.8地震数字波形数据用于建立近震震级与面波震级间的转换关系(图 1),使用46次ML≥4.5地震波形数据建立近震震级与宽频带面波震级间的转换关系(图 2)。
2 震级的测定
近震震级ML、面波震级MS以及宽频带面波震级MS(BB)均按照2017年版《地震震级的规定》(GB17740-2017)(刘瑞丰等,2017)进行测定。
2.1 近震震级ML
近震震级ML是使用仿真DD-1短周期地震仪记录的S波或Lg波的最大振幅,通过下式(刘瑞丰等,2015)计算得到
|
$
{M_{\rm{L}}} = {\rm{lg}}A + R\left( \mathit{\Delta } \right)
$
|
(1) |
其中,A为水平向最大地动位移,A=(AN+AE)/2,单位m;AN、AE分别为SN、EW向S波或Lg波的最大振幅,单位m;R(Δ)为近震震级的量规函数。
2.2 面波震级MS
针对浅源地震(h≤60km)的面波震级MS,应将原始宽频带记录仿真成基式(SK)中长周期地震仪记录,使用面波地动位移的最大振幅和相应的周期,采用如下公式(刘瑞丰等,2015)计算得到
|
$
{M_{\rm{S}}} = {\rm{lg}}\left( {\frac{A}{T}} \right) + 1.66{\rm{lg}}\left( \mathit{\Delta } \right) + 3.5
$
|
(2) |
其中,A为地震面波地动位移的最大振幅,取两水平分向地动位移的矢量和,单位m;Δ为震中距,适用范围为2°<Δ<130°;T为A对应的周期,单位s,依下式求得(刘瑞丰等,2015)
|
$
T = \frac{{{T_N}{A_N} + {T_E}{A_E}}}{{{A_N} + {A_E}}}
$
|
(3) |
2.3 宽频带面波震级MS(BB)
对于浅源地震(h≤60km)的面波震级MS(BB),直接在垂直向速度型宽频带记录上量取面波质点运动速度的最大振幅,采用下式(刘瑞丰等,2015)得到
|
$
{M_{{\rm{S}}({\rm{BB}})}} = {\rm{lg}}\left( {\frac{{{V_{{\rm{max}}}}}}{{2\pi }}} \right) + 1.66{\rm{lg}}\left( \mathit{\Delta } \right) + 3.3
$
|
(4) |
式中,Vmax为垂直向面波质点运动速度的最大值,单位μm;Δ为震中距,适用范围为2°<Δ<160°;T为Vmax对应的面波周期,3s<T<60s。
本文依据式(1)、(2)、(4),重新测定了330个近震震级ML和面波震级MS对以及98个宽频带面波震级MS(BB),共计758个震级数据,用于矫正近震震级与面波震级间的转换关系、新建近震震级与宽频带面波震级间的转换关系。
3 回归方法
基于1范数线性回归和2范数正交回归方法(Carroll et al,1996),对内蒙古测震台网测定的ML与MS、ML与MS(BB)之间的转换关系进行分析。
3.1 线性回归方法
对于2个或多个存在统计相关的随机变量,可根据大量的观测数据来确定它们之间定量的统计关系,即求出一定的数学公式来表达这些关系,这种公式被称作回归方程(刘瑞丰,2007)。考虑将N个数据点(xi,yi)(i=1,2,3,…,N)拟合成如下式所示的直线模型
众所周知,对于相同的样本点,选择不同的自变量和因变量,会得到不同的回归方程,即选择X方向还是Y方向拟合,所得的回归直线是不同的(孙彦清,2002;刘瑞丰等,2007)。如果要确定直线型经验公式Y=AX+B中的A和B,就要先根据测量的误差来判断误差方向,然后,再利用误差方向来确定拟合方向(黄杰等,2000;孙彦清,2002)。
通常利用线性最小二乘回归(SR)方法就可以确定系数A、B。Gutenberg等(1956a、1956b)采用SR方法给出了MS与ML之间的关系式。SR回归方法适用于一个变量产生的偏差比另一个变量产生的偏差大的情况。确定系数A、B拟合式(5)时有以下2种可能(Draper et al,1998)
|
$
{\rm{S}}{{\rm{R}}_1}\;\;\;\;Y \leftarrow {A_1}X + {B_l}
$
|
(6) |
适用条件为σxx2→0和σyy2>0,其中,σxx2、σyy2分别为x、y的方差;
为x、y的这种情况又称为反标准回归,适用条件为σxx2>0和σyy2→0。
3.2 正交回归方法
当2个变量均有可能发生较大变化,即当X、Y方向上的测量误差均不可忽略时,拟合不能在单一方向上进行。在这种情况下,拟合的直线应满足各测量点到拟合直线的垂直距离的平方和为最小,即正交拟合(吴俊林等,1992;李雄军,2005a、2005b;姜慧等,2006)。正交回归方法能够克服固定单方向最优所带来的拟合稳定性差的弊端。以OR表示正交回归方法,则有
|
$
{\rm{OR}}\;\;\;\;Y = {A_3}X + {B_3}
$
|
(8) |
通常采用Hesse表示方法来表示正交回归,即将2个变量都放在等号的右边,表示右边的2个变量都在变化,即
|
$
P = {n_x}X + {n_y}Y
$
|
(9) |
式中,P=B3/q,nx=-A3/q,ny=1/q,q=(1+A32)1/2,-nx/ny=A3。X、Y的系数A3和B3同时除以q,使其符合Hesse表示方法。
如果将式(6)、(7)应用于震级标度Mx和My,则SR1方法适用于在Mx测量偏差较大的情况下对My产生的影响,而SR2方法则适用于在My测量偏差较大的情况下对Mx产生的影响。然而,由于所有的震级在测量时都有可能存在一定的误差,无论是SR1还是SR2,其所得结果都与实际震级有一定的差别,因此,从理论上讲,利用正交回归方法研究各种震级标度之间的关系应当更能接近实际震级(Madansky,1959;Fuller,1987;刘瑞丰等,2007)。为便于比较,本文分别给出了利用1范数SR1、SR2和2范数OR方法得到的不同震级标度之间的关系式,但在对结果的分析和结论中则主要依据利用OR方法得出的拟合关系式。
4 近震震级与面波震级间的转换关系
基于线性回归和正交回归方法,获得近震震级ML与面波震级MS间的转换关系;同时采用高斯扰动方法,对每个点进行高斯随机扰动,对扰动后的数据进行回归分析;将最终结果与郭履灿获得的经验关系①进行对比分析。
4.1 ML与MS间的转换关系
4.1.1 线性回归和正交回归
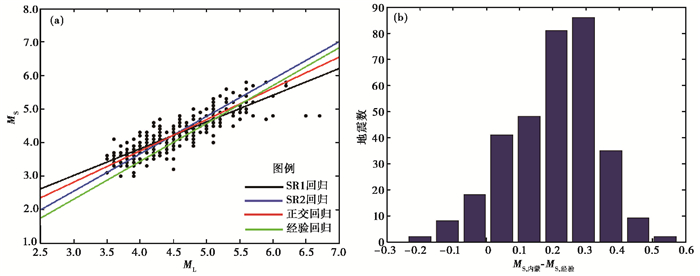
基于一般线性回归方法(SR1和SR2)和正交回归方法(OR),对2008年1月~2015年10月的116次地震的重测震级ML和MS(共329个震级对)进行了线性回归,震级范围为3.8≤MS≤6.7。表 1给出了经线性回归和正交回归得到的ML与MS间的关系式,图 3(a)为由线性回归(SR1和SR2)、正交回归(OR)以及郭履灿经验关系式①MS,经验=1.13ML-1.08得到的4条ML与MS关系曲线。由图 3(a)可见,由正交回归方法(OR)得到的曲线位于数据点的中间,且均方根误差最小,为最佳拟合曲线。由此得到内蒙古地区重新矫正后的近震震级ML与面波震级MS间的转换关系为
|
$
{M_{{\rm{S,内蒙}}}} = 0.96{M_{\rm{L}}} - 0.10
$
|
(10) |
表 1

表 1 ML震级与MS震级间的关系
| 震级 |
地震数量 |
震级范围 |
回归方法 |
关系式 |
RMS(均方根误差) |
| ML-MS |
116 |
3.8≤MS≤6.7 |
SR1 |
MS ←0.80ML+0.60 |
±0.32 |
| SR2 |
MS →1.16 ML-1.02 |
±0.34 |
| OR |
MS=0.96ML-0.10 |
±0.24 |
|
表 1 ML震级与MS震级间的关系
|
图 3(b)给出了MS,内蒙与MS,经验差值数量分布情况。由图 3(b)可见,差值绝大多数分布在0. 0~0. 4之间,其中,以MS,内蒙-MS,经验=0.3的数量最多。可见,内蒙古地震实测MS,内蒙与MS,经验值相差较大。
4.1.2 高斯随机扰动
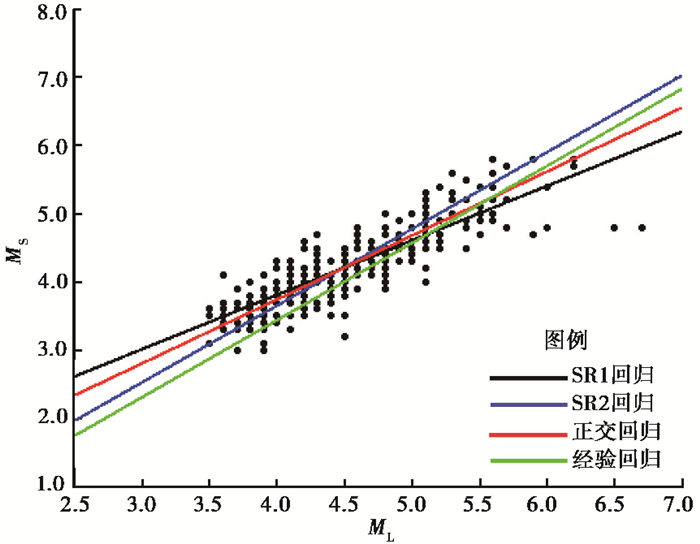
利用上述329个ML、MS震级对数据,采用Matlab平台自带函数noral,对329对数据进行高斯扰动。扰动过程中震级MS添加均值为0,方差为0.2。扰动后,对高斯扰动后的数据进行线性回归(SR1和SR2)和正交回归(OR),表 2给出了经高斯扰动后线性回归和正交回归得到的ML与MS间的关系式,图 4为经过高斯扰动后的线性回归(SR1和SR2)、正交回归(OR)以及由郭履灿经验关系回归得到的4条曲线。
表 2

表 2 经高斯扰动后ML震级与MS震级间的关系
| 震级 |
地震数量 |
震级范围 |
回归方法 |
关系式 |
RMS(均方根误差) |
| ML-MS |
116 |
3.8≤MS≤6.7 |
SR1 |
MS ←0.79ML+0.66 |
±0.37 |
| SR2 |
MS →1.23 ML-1.31 |
±0.37 |
| OR |
MS=0.98ML-0.16 |
±0.27 |
|
表 2 经高斯扰动后ML震级与MS震级间的关系
|
由表 2、图 4可见,高斯扰动前、后近震震级ML与面波震级MS间的转换关系变化不大,系数A由0.96变为0.98,增加了0.02;系数B由0.10变为0.16,增加了0.06。
4.2 2种震级转换关系的对比分析
分析式(10)与郭履灿经验公式①MS,经验=1.13ML-1.08的两种震级转换关系、两种转化关系的实测值MS,经验、MS,内蒙以及MS,经验与MS,内蒙的差值分布情况可知:
(1) 从2种震级转换关系式整体来看,差别较大。系数A由1.13降为0.96,降低了0.07,变化不大;系数B变化较大,两者明显存在系统偏差。这种差别可能是由区域构造特征的差异性所致。
(2) 由本文实测的ML经式(10)转换得到的MS,内蒙值,明显高于由MS,经验=1.13ML-1.08转换得到的MS,经验值,平均差值为0.23,故建议使用式(10)。
(3) 分析MS,经验与MS,内蒙差值数量分布情况(图 3(b))可知,绝大多数地震震级差值为0~0.4,在0.2~0.3间的地震数量最多。
(4) 表 3给出了3.0≤ML≤7.0震级范围内关系式MS,经验与MS,内蒙的对照,可以看到,二者相差的震级范围为0~0.5。
表 3

表 3 3.0≤ML≤7.0震级范围内关系式MS,内蒙与MS,经验的对照
| ML |
内蒙古地区关系式MS,内蒙 |
经验关系式MS,经验 |
MS,内蒙-MS,经验 |
| 3.0 |
2.8 |
2.3 |
0.5 |
| 3.5 |
3.3 |
2.9 |
0.4 |
| 4.0 |
3.7 |
3.4 |
0.3 |
| 4.5 |
4.2 |
4.0 |
0.2 |
| 5.0 |
4.7 |
4.6 |
0.1 |
| 5.5 |
5.1 |
5.1 |
0.0 |
| 6.0 |
5.6 |
5.7 |
0.1 |
| 6.5 |
6.1 |
6.3 |
0.2 |
| 7.0 |
6.5 |
6.8 |
0.3 |
|
表 3 3.0≤ML≤7.0震级范围内关系式MS,内蒙与MS,经验的对照
|
5 结论
本文基于1范数线性回归(SR1和SR2)和2范数正交回归(OR)等3种方法,通过对内蒙古地区2008年1月~2015年11月116次ML≥3.8地震的近震震级ML和面波震级MS的重新实测,校正了郭履灿的经验震级转换关系①,获得了内蒙古地区近震震级ML与面波震级MS间的转换关系,并得到以下结果:
(1) 由线性回归(SR1和SR2)与正交回归(OR)方法所得的ML与MS关系曲线可知,正交回归方法(OR)得到的曲线位于数据点的中间,且均方根误差最小,为最佳拟合曲线,故内蒙古地区近震震级ML与面波震级MS间的转换关系应为MS,内蒙=0.96ML-0.10。
(2) 基于Matlab平台中的高斯扰动函数,对每个点采用高斯随机扰动,高斯扰动前、后近震震级和面波震级间的转换关系变化不大。
(3) 分析MS,经验=1.13ML-1.08和MS,内蒙=0.96ML-0.10可知,两者间明显存在系统偏差,这种差别可能是由区域构造特征的差异性所致。
(4) MS,内蒙值明显高于MS,经验值,平均差值为0.2。结果表明,近震震级经验转换关系已不适合内蒙古地区的区域特征,建议使用矫正后的近震震级ML与面波震级MS间的转换关系式。
(5) 关系式MS,经验与MS,内蒙的差值数量分布情况显示,绝大多数地震震级差值为0~0.4,0.2~0.3间的地震数量最多。可见,MS,内蒙与MS,经验值相差较大。
(6) 由3.0≤ML≤7.0震级范围内关系式MS经验与MS,内蒙的对照表可见,二者相差的震级为0~0.5。
(7) 由于本研究所选时段ML≥3.8地震数量不多,且地震分布不均匀,因此,本文所得结果还有待在今后的实际使用过程中不断完善,以使其更加符合内蒙古地区的区域特征。
致谢:
感谢刘瑞丰研究员为本研究提供计算程序及帮助。
 2017, Vol. 33
2017, Vol. 33