2. 新疆维吾尔自治区地震局喀什基准地震台, 新疆喀什 844000
2. Kashgar Seismic Station of Earthquake Administration of Xinjiang Uygur Autonomous Region, Kashgar 844000, Xinjiang, China
地震波在地球介质中转播时会很快衰减殆尽,造成这种现象的原因主要是地球介质的非完全弹性以及介质弹性的非均匀性。Q值是描述地球介质特性的主要参数,地壳中裂隙状态、流体迁移、热物质上涌等岩性变化都可能引起应力变化,从而造成品质因子Q值的变化(周慧兰,1990)。Aki(1969)首次提出了尾波散射理论,提出可以利用尾波来研究震源区上部岩石圈的横向不均匀性、区域地震活动性以及震源机制解等。Aki等(Aki,1969;Aki et al,1975)在单次散射模型基础上提出了台、源重合情况下的尾波衰减系数计算方法。考虑到台、源分离情况下震源至接收点距离的影响,Sato(1977)和Pulli(1984)对Aki等(1975)的尾波计算方法进行了必要的修正(即Sato模型)。
尾波Q值主要反映了以震源和记录台站为焦点的椭球范围内的介质品质因子的特性,该品质因子作为衡量地区构造活动的重要指标,在震源物理、工程地震学和地震预测研究中都有重要的应用。与其他研究方法相比,利用尾波散射理论能较好地描述介质的某些特征,其优点在于它不是对介质进行确定的测量,而是给出介质在统计平均意义上的特征描述(李琼等,2007)。诸多研究表明,Q值在地震活动频繁的地区较低,在地震活动相对平静的地区较高;在古老的地质单元或构造运动稳定地区较高,而在近代地质单元或构造活跃地区较低(马云生等,1995;李白基等,2004;朱新运,2006:朱新运等,2006a、2006b;马力等,2010;师海阔等,2011;贺永忠等,2012)。
本文利用南天山西段2009~2014年10个台站各自附近60km范围内的数字化地震波形资料,采用Aki尾波单次散射模型,对南天山西段的地震尾波Q值进行了研究。
1 研究区域及观测资料研究区域位于新疆南天山西段(37.0°~43.0°N,73°~82°E)。该区域中小地震丰富,地质构造比较复杂。喀什-乌恰交汇区是新疆地震活动最为强烈的地区之一,位于帕米尔弧的北段,是南天山与西昆仑2条地震带的交汇区,区域内构造运动强烈,地壳缩短速率可达20mm/a,活动断裂分布密集,主要断裂有托特拱拜孜断裂、卡兹特-阿尔特断裂、乌鲁克恰特断裂以及塔拉斯-费尔干纳断裂等(冯先岳,1995;曲延军等,2010)。
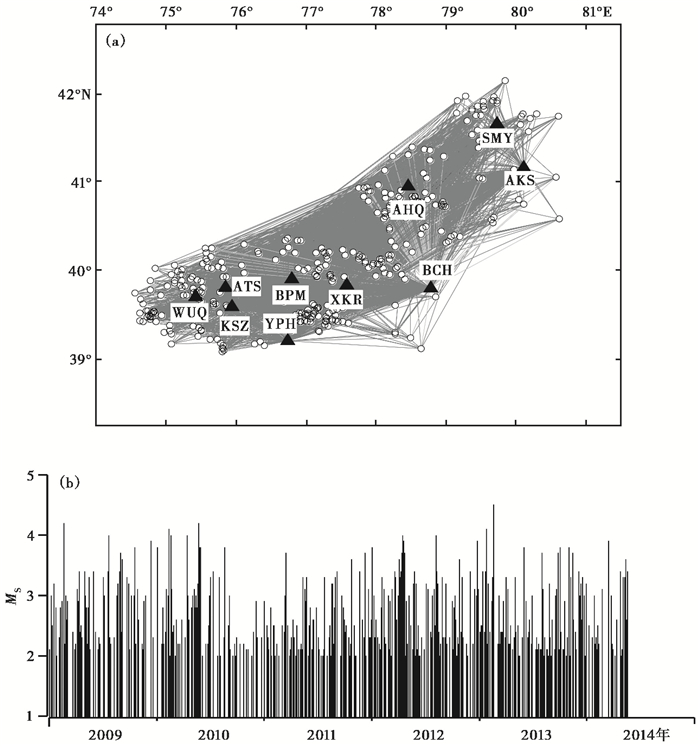
本研究使用南天山西段10个台站的记录,各台站的基本情况见图 1(a)及表 1。所选地震台站的地震仪是以CMG和CTS型为主的甚宽频带地震仪,其采样率均为100Hz,频率在0.1~30Hz之间,均具有平坦的速度响应。选取分析样本为新疆台网地震目录的起止时间为2009年1月~2014年4月,震中在南天山西段(37.0°~43.0°N,73°~82°E),震级为MS2.0~4.5的地震。其中MS2.0~2.9地震243次,MS3.0~3.9地震141次,MS4.0~4.5地震13次,最大地震为2013年2月18日阿图什4.5级地震。所用地震波形记录清晰,噪声水平满足计算条件(图 1(b))。
|
图 1 (a) 研究区台站、地震分布及射线路径,(b)MS≥2.0地震M-T图 ▲代表台站,○表示震中 |
| 表 1 研究区域地震台站信息情况 |
本文采用尾波方法求解Q值,用单次散射模型描述尾波衰减(Aki et al,1975),根据该单次散射模型,以某一中心频率的一定带宽滤波器滤波后的尾波振幅可表述为
| $ A\left( {f,t} \right) = S\left( f \right) \cdot {t^{ - u}} \cdot {{\rm{e}}^{ - \pi ft/{Q_{\rm{C}}}(f)}} $ | (1) |
式中,S(f)为震源因子;t为发震时刻算起的地震波流逝时间;u为常数,且体波的u=1、面波的u=0.5,因本文主要进行近震数据的分析,故u取值为1;QC(f)为对应于中心频率点f的尾波Q值,A(f,t)是对应t时刻一个采样周期的幅度最大值。
对式(1)两边取自然对数,进而整理变换为
| $ {\rm{ln}}(A\left( {f,t} \right) \cdot {t^u}) = {\rm{ln}}S\left( f \right) - a \cdot t $ | (2) |
式中,
| $ {Q_{\rm{C}}}\left( f \right) = - \pi f/a $ | (3) |
计算中首先对地震尾波以f为中心频率,
| $ Q\left( f \right) = {Q_0}{f^\mu } $ | (4) |
式(4)给出了QC(f)值与f的关系,对此式两边取对数可得
| $ {\rm{ln}}{Q_{\rm{C}}}\left( f \right) = {\rm{ln}}{Q_0} + \eta {\rm{ln}}f $ | (5) |
从式(5)可以看出,由于lnQC(f)与lnf成线性关系,采用最小二乘法可以得出Q0和η值。
3 数据处理及结果分析 3.1 数据处理本研究分析频率段为4~18Hz,间隔1Hz,对应中心频率f,宽带取
|
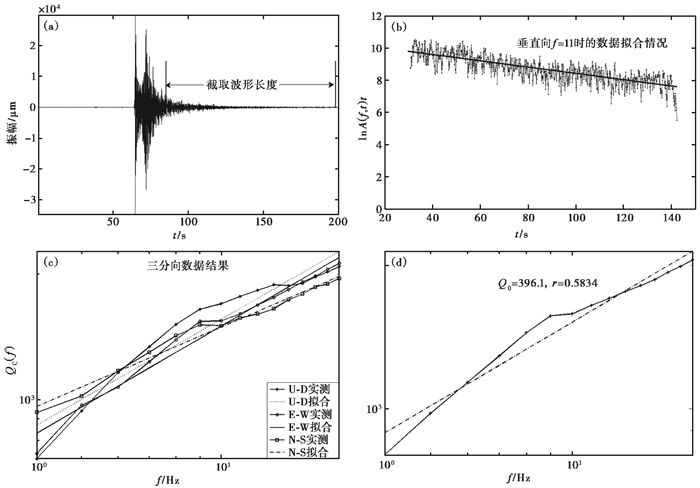
图 2 2010年5月14日23时31分MS2.1地震的阿合奇(AHQ)台计算实例 (a)尾波截断;(b)垂直向f=11Hz时的数据拟合结果;(c)三分量数据结果;(d)平均数据结果 |
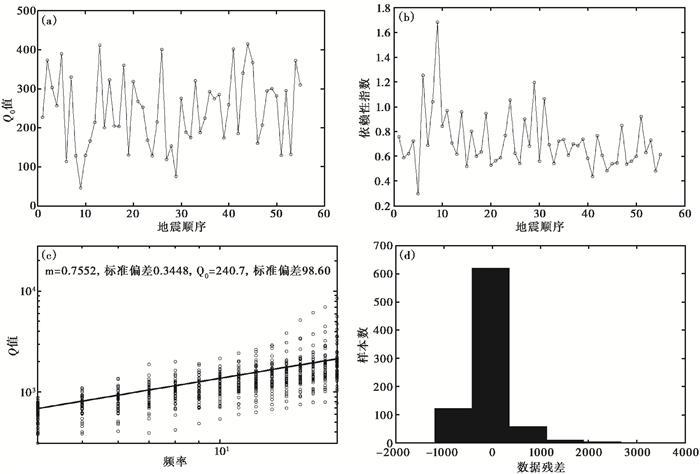
图 3和表 2给出了以阿合奇台为中心60km范围内58次地震计算出来的Q0值和η值。由表 2可见,阿合奇台附近尾波Q0值在53~442之间,Q0值平均值为249,η值均值为0.73。
|
图 3 阿合奇台Q0值与频率关系 (a)Q0值变化;(b)指数变化;(c)Q0值与频率的关系;(d)拟合残差 |
| 表 2 阿合奇县地震尾波Q0值结果 |
近年来,许多研究者利用地震尾波衰减探索了QC值大震前后的变化,以期借此发现大震的前兆信息。多数研究结果表明,主震前QC值变小,主要表现在12Hz以下的频率范围,但也有QC值在震前变大的结果(Sato et al,1988)。马宏生等(2005)认为,大震前由于受较强应力作用,地壳介质特别是韧性层破裂的增加可使尾波QC值减小(QC-1值变大),但临近破裂时,由于应力增强,导致裂隙闭合,QC值反而增大;大震后,由于作用在地壳韧性层的应力得到释放,从而介质松弛,以至反映其介质衰减特征的QC值减小,1976年的唐山地震就具有这个特点。
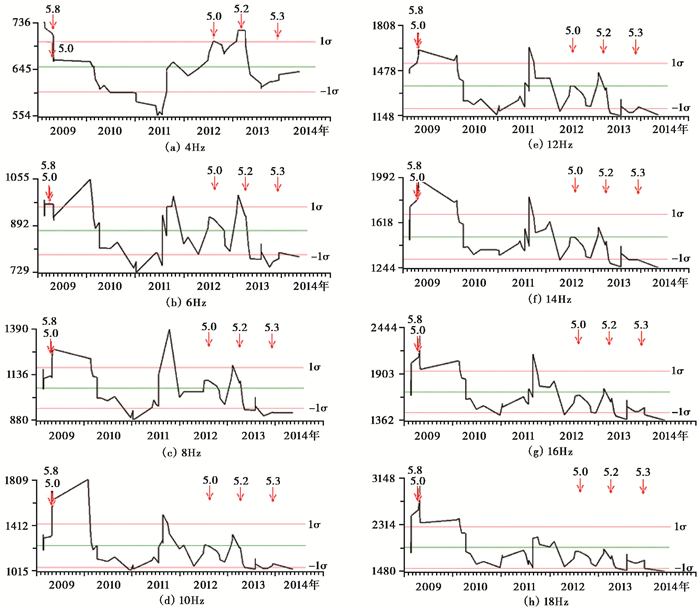
图 4给出了2009年1月~2014年4月阿合奇台附近60km范围内MS≥2.0以上地震在4.0、6.0、8.0、10.0、12.0、14.0、16.0、18.0Hz中心频段QC随时间的变化过程,图中还同时标出了台站周围100km范围内5级以上地震分布。由图 4可见,图中8个频段QC值变化形态基本一致,其中4.0Hz时的QC值时间进程图较为平滑,2012年8月11日5.0级地震以及2013年3月11日5.1级地震前几个频段均出现QC值高值;震后呈现下降趋势。
|
图 4 2009~2014年阿合奇台周围60km MS≥2.0地震分频QC值时序进程图 图(a)~(h)分别对应4~18Hz时QC值,红色横线为1倍准方差,绿色横线为均值 |
通过上述数据处理过程,对研究区域内的10个台站60km范围内MS≥2.0以上地震在4.0、6.0、8.0、10.0、12.0、14.0、16.0、18.0Hz中心频段QC值随时间的变化过程进行分析。
南天山西段台站分布不是十分均匀,该区域所发生地震的位置常呈随机的聚散状,各台能记到其周围可供进行尾波QC值计算的地震并不相同。由于符合单次散射模型尾波功率谱分析的地震波形样本所限,有的台记录波形样本数较多,有的较少。10个台站不同频段QC值时序进程分析结果表明,不同台站的分频QC值时序进程曲线趋势各异,但每个台站在不同频率的时间进程曲线趋势大致一致。
3.4 尾波衰减特征QC值研究基于近震尾波的单次散射理论,我们利用南天山西段10个台记录的397个信噪比较高的地震数字化波形资料,计算了该地区地球介质对不同频率地震波衰减的品质因子QC。表 3和图 5给出了研究区域内10个台站为中心60km范围内地震事件计算得到的Q0和η值的平均值结果。
| 表 3 南天山西段10个台站周围地震事件计算的Q0与η值平均值 |
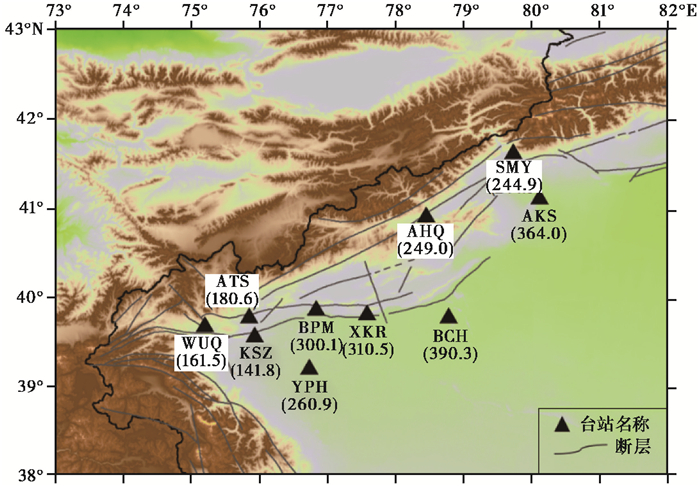
|
图 5 南天山西段各台站附近尾波Q0值与主要活动构造分布 |
由表 3可看出,南天山西段Q0值的平均值在140~390之间,频率相关系数η的平均值在0.62~1.00之间,拟合平均QC值与对应频率之间的关系结果为QC=261.2±110.8f0.80±0.28,本文计算结果与李志海等(2011)对伽师地区Q0的计算结果基本一致;与赵翠萍等人(2011)得到的天山中段地区Q值(Q=Q0fη=344.1f0.553)相比较则显现为南天山西段的Q0值小于天山中段地区的Q0值。傅承义等(1983)研究认为,Q值与介质均匀程度相关,或者说与介质强度有关。稳定地区介质均匀程度较高,其Q值较大;构造活动强烈地区介质均匀程度较低,其Q值较小。据此认为,南天山西段构造活动要强于天山中东段,这与两个地区地震活动特征是一致的:南天山西段是我国地震活动最强烈的地区之一,以6级以上地震活动为主;而天山中段地震活动相对南天山西段要弱,以5级地震为主。巴楚台附近的Q0值最高,达到390.3。研究区域10个台站Q0值从大到小依次为:巴楚、阿克苏、西克尔台、八盘水磨、阿合奇、神木园、岳普湖、阿图什、乌恰及喀什。从分布来看,塔里木盆地边缘的阿克苏、巴楚和西克尔台较高的Q0值反映盆地边缘介质的整合性相对较好,不像其他区域那样破碎,与其他几个台站附近的尾波Q0值相比较而言,对地震波的散射较强。喀什和乌恰台附近Q0值最小,反映该地区地壳破碎程度较高,与其较高的地质构造活动和较强地震活动水平相符合。
本文η值的部分计算结果出现了大于1的情况,表明频率越高,衰减率越小,这与介质对地震波的吸收是随频率升高而增强的一般认识相悖。而马云生等(1995)和马力等(2010)在计算云南滇西实验场地区的尾波QC值、北京及其周围地区以及昆明台附近尾波QC值分布特征的研究中,也出现过类似的现象。本文中讨论的QC值是实际观测资料按散射理论模式直接拟合得到的,有些η值大于1的原因,尚待进一步研究解释。
4 结语Q值大小反映了地震波衰减程度,Q值对频率的依赖性与介质均匀程度有关,依赖程度越大,地壳介质均匀程度越低,相关区域构造活动越强烈,地震活动水平越高(朱新运等,2006a、2006b)。本文依据Aki尾波单次散射模型,利用南天山西段10个台站附近地震事件频带资料计算了相应的尾波QC值,计算得到介质品质因子Q0值的平均值在140~390之间,频率相关系数η的平均值在0.62~1.00之间。从Q0值大小分布来看,喀什、乌恰、阿图什等台站Q0值最小;与不同区域Q值及频率相关系数相比较,本文研究区的Q0值较低,这与本地区的地震活动性相一致,表明该地区是以低Q0高η值为特征的构造活跃区。
| 冯先岳. 1995, 天山全新世活动断裂及古地震研究. 内陆地震, 9(3): 217–226. |
| 傅承义, 陈运泰, 祁贵中. 1983, 地球物理学基础. 北京: 科学出版社. |
| 贺永忠, 师海阔, 朱新运, 等. 2012, 利用两种模型对宁夏及邻区尾波Q值进行对比研究. 大地测量与地球动力学, 32(增刊): 10–17. |
| 马宏生, 刘杰, 张国民, 等. 2005, 尾波QC值随时间变化在地震预测中应用的研究. 地震, 25(4): 39–48. |
| 马力, 雷湘鄂, 孙和平. 2010, 昆明台附近区域地震尾波Q值分析. 地震学报, 32(6): 670–679. |
| 马云生, 张天中, 张焕生. 1995, 北京及其周围地区尾波Q值分布特征的研究. 地震学报, 17(1): 448–458. |
| 李白基, 秦嘉政, 钱晓东. 2004, 云南姚安地区的尾波衰减. 地震学报, 26(1): 47–52. |
| 李白基, 秦嘉政, 钱晓东. 2007, 年宁洱6.4级地震余震序列尾波Q值研究. 地震研究, 30(4): 337–343. |
| 李志海, 朱成英, 夏爱国, 等. 2010, 新疆伽师地区非弹性衰减、场地响应与震源参数研究. 中国地震, 26(3): 340–348. |
| 曲延军, 王琼, 聂晓红. 2010, 新疆南部构造区带与地震活动状态研究. 内陆地震, 24(4): 298–306. |
| 师海阔, 朱新运, 贺永忠, 等. 2011, 利用Aki模型对宁夏及邻区尾波Q值的研究. 西北地震学报, 33(4): 370–375. |
| 赵翠萍, 陈章立, 华卫, 等. 2011, 中国大陆主要地震活动区中小地震震源参数研究. 地球物理学报, 54(6): 1478–1489. |
| 周慧兰, 1990, 地球内部物理, 218~227, 北京: 地震出版社. |
| 朱新运. 2006, 影响尾波Q值数据结果的算法因素分析. 东北地震研究, 22(4): 8–13. |
| 朱新运, 张帆. 2006a, 浙江及邻区尾波Q值研究. 西北地震学报, 28(2): 108–113. |
| 朱新运, 刘杰, 张帆. 2006b, 基于Aki模型的近震S波尾波Q值求解及分析软件研制. 地震研究, 29(1): 76–80. |
| Aki K. 1969, Analysis of seismic coda of local earthquakes as scattered wave. J Geophys Res, 74: 615–631. DOI:10.1029/JB074i002p00615. |
| Aki K, Chouet B. 1975, Origin of the coda wave:Source, attenuation and scattering effects. J Geophys Res, 80(B23): 3322–3342. |
| Pulli J. 1984, Attenuation of coda wave in New England. Bull Seism Soc Amer, 74(4): 1149–1166. |
| Sato H. 1977, Energy propagation including scattering effects:Single isotropic scattering approximation. J Phys Earth, 25: 27–41. DOI:10.4294/jpe1952.25.27. |
| Sato H. 1988, Temporal changes in scattering and attenuation associated with the earthquake occurrence-A review of recent studies on coda waves. Pure App Geophys, 126: 465–497. DOI:10.1007/BF00879007. |
 2017, Vol. 33
2017, Vol. 33


