基于水库气枪震源数据的频域水准比例因子反褶积方法分析
游秀珍, 李军, 林彬华, 黄艳丹, 巫立华, 郭阳
中国地震  2018, Vol. 34 2018, Vol. 34 Issue (1): 14-24 Issue (1): 14-24
|
自20世纪60年代以来,气枪震源在海洋石油勘探中得到广泛应用,积累了大量宝贵经验。随着气枪震源技术的日益成熟,为使人工气枪震源能在地球物理探测领域也发挥作用,研究人员发展了更低频率的震源——大容量气枪震源。大容量气枪震源以激发能量大、低频成分丰富、可操控、可重复、成本低、破坏性小、绿色无污染等特点受到越来越多的关注。近些年来,国内地震科学研究人员利用大容量气枪震源开展了一系列深部结构探测科学实验,如福建陆域及中国台湾海峡西部地区陆海联合探测实验和地学长江计划实验等,并在云南宾川、新疆呼图壁和甘肃张掖建设了地震信号发射台用以监测地下介质性质的变化(陈颙等,2016;王宝善等,2016)。
水库气枪实验中,由于水库容积小,高压气泡在水库中产生剧烈振动,同时出现长时间的振荡子波,因而导致激发的气枪震源信号不完全重复,进而影响地下介质变化的监测精度。因格林函数可反映研究区域地下介质的信息,地震学家们提出利用反褶积方法获取气枪震源至接收台站之间的近似格林函数以消除震源的影响(王宝善等,2012;栾奕等,2016)。刘自凤等(2015)、魏芸芸等(2016)在利用气枪震源识别地壳介质波速变化之前都先进行反褶积处理以排除震源变化的干扰。王宝善等(2012)通过比较交叉干涉与互相关方法认为,反褶积的结果虽然信噪比较低,但是能较好地去除激发环境的影响。翟秋实等(2016)对比了频率域和时间域反褶积的效果,指出频率域反褶积计算效率有优势,但信噪比不如时间域反褶积。
前人的相关工作侧重利用反褶积直接处理数据,或是与其它方法的效果进行比较,而对频率域水准反褶积方法计算存在的问题鲜有研究。本文采用频率域水准比例因子反褶积方法和互相关时延检测技术,研究反褶积方法引入的水准比例因子取不同值时对反褶积计算结果的影响,以及台站的背景噪声水平对计算结果的影响,并分析反褶积法消除震源影响的效果。
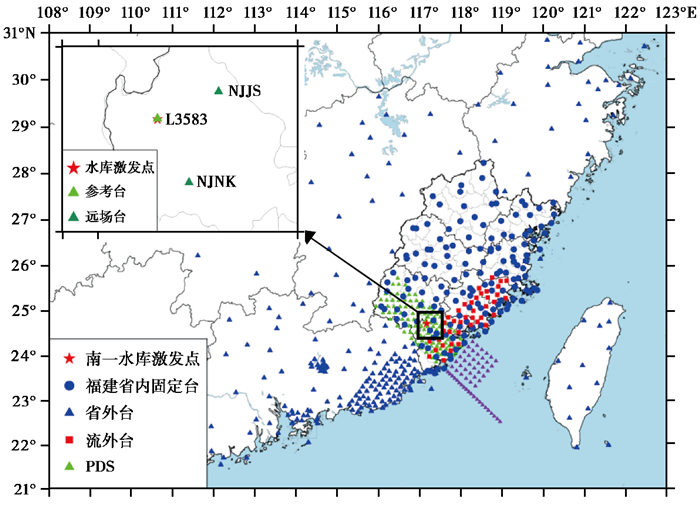
1 水库气枪实验概况2016年12月,福建省地震局在漳州南靖南一水库开展主动源探测实验。实验使用福建省地震局自主设计组装的大容量气枪震源系统,选用4支Bolt-1500LL型气枪组合阵列,其单支气枪容量为2000 in3,枪阵总容量达8000 in3。枪阵尺寸为7m×7m,沉放深度为12m,每一工况实验定点激发9次。实验观测系统由陆海台阵构成:陆域台阵包括88个福建测震台、福建周边(广东、江西、浙江、湖南和中国台湾)部分测震台站、40个实时传输的流动台和100个PDS(非实时传输的野外流动台);海域台阵由57套OBS形成的网格状台阵组成。本文选取资料时考虑到气枪记录信号的清晰度,选择震中距为200m的岸边测震台L3583为近场参考台,震中距为18.53km的测震台NJJS和震中距为19.05km的测震台NJNK为远场台站(图 1)。
|
图 1 南一水库气枪激发位置及实验观测台站分布 |
地震波数据包含震源函数、震源与地震仪器之间的格林函数、仪器响应和地面运动噪声,可将其表示为
| $ u\left(t \right) = s\left(t \right) * g\left(t \right) * i\left(t \right) + n\left(t \right) $ | (1) |
式中,u(t)为地震仪器记录的数据;s(t)为震源时间函数;g(t)为格林函数;i(t)为仪器响应;n(t)为噪声。
我们把靠近气枪震源的近场台站信号当作近似的震源时间函数,由于实验期间观测设备没有发生变化,因此,不考虑仪器响应的影响,同时忽略噪声影响。将远场台站和近场台站记录分别进行傅里叶变换,再相除即为频率域反褶积
| $ G\left(\omega \right) = \frac{{U\left(\omega \right)}}{{S\left(\omega \right)}} $ | (2) |
式中,G(ω)为近似格林函数的频谱;U(ω)为远场台站气枪记录的频谱;S(ω)为近场台站气枪记录的频谱。由于式(2)中分母可能出现为零或者趋于零的情况,以致频率域的除法不稳定。采用Helmberger等(1971)提出的频率域因子反褶积方法,将式(2)改进为
| $ G\left(\omega \right) = \frac{{U\left(\omega \right) \cdot {S^ * }\left(\omega \right)}}{{\max \left\{ {S\left(\omega \right){S^ * }\left(\omega \right), \max \left\{ {S\left(\omega \right){S^ * }\left(\omega \right), } \right\}c} \right\}}} $ | (3) |
式中,S*(ω)为S(ω)的复共轭;max为求最大值运算符;c为水准比例因子。
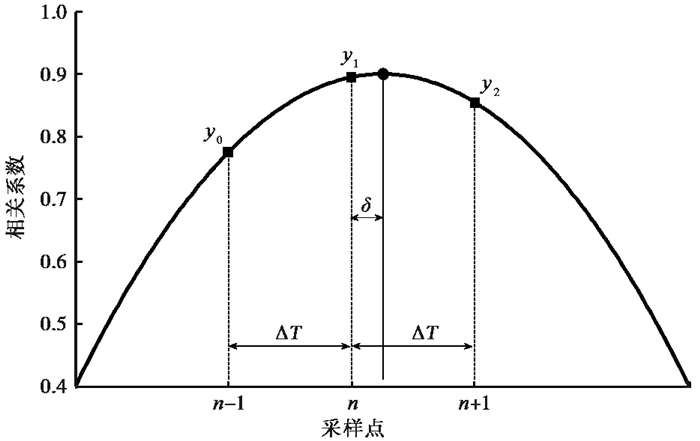
2.2 互相关时延检测方法互相关时延检测方法是一项被广泛应用的成熟技术,其原理是以不同时延计算两列相似波形的互相关系数,互相关系数最大时所对应的时间延迟,即是两列波形的延时。互相关时延测量是以一个采样间隔作为步进的,然而相关函数的最大峰值通常并不落在采样点上而是偏离采样点,这可以通过拟合的方式解决以获得更高的时间测量精度(Céspedes et al,1995)。为此,本文采用抛物线拟合方法重建相关函数,得到新相关函数的峰值和其对应的位置(图 2)。拟合前后相关函数峰值对应位置的时间延迟计算公式为
| $ \delta = \frac{{\left({{y_0} - {y_2}} \right)\Delta T}}{{2\left({{y_0} + {y_2} - 2{y_1}} \right)}} $ | (4) |
|
图 2 抛物线拟合曲线 圆点为拟合后最大相关系数的位置;方点为拟合前相关函数峰值相邻采样点对应的位置 |
式中,y1为拟合前的最大相关系数;y0和y2分别为拟合前相关函数峰值相邻采样点对应的相关系数;ΔT为采样时间间隔。
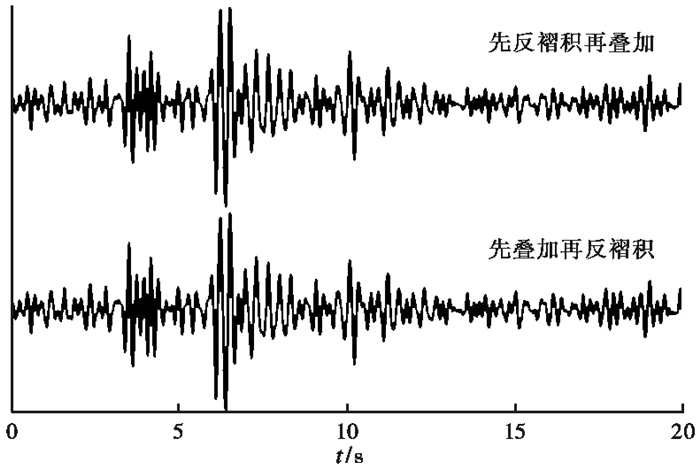
3 计算结果以2016年12月南一水库A09工况为例,先根据气枪的激发时间将原始波形进行分段截取,再将垂向分量记录进行去均值、2~8Hz滤波、归一化等预处理,图 3是参考台L3583和远场台NJNK预处理后的波形。由于工况实验持续时间不足半小时,其间未发生有影响的地震,且水库水位基本稳定,故可认为地下介质是不变的。在实验过程中装载气枪的浮台会随气枪激发发生偏移,因此,福建省地震局的工作人员采用悬挂重物、绳索固定等方式对浮台进行固定,根据浮台上安装的GPS监测结果可知,激发位置的变化较小,基本控制在1m以内。我们首先分析反褶积与叠加的先后顺序对结果的影响。图 4为NJNK台的计算结果,将不同顺序计算的近似格林函数做互相关,得到互相关系数峰值为0.999,可见反褶积与叠加的先后顺序对最终结果的影响较小,因此,进行数据处理时先叠加再反褶积计算。

|
图 3 L3583、NJNK台预处理后的波形 |
|
图 4 不同顺序计算的近似格林函数对比 |
频率域水准反褶积方法引入水准比例因子以获得合理的水准阈值,计算时使分母中频谱振幅小于阈值的提升至阈值,从而提高反褶积计算结果的稳定性。为探究水准因子对反褶积结果的影响,在相同情况下,设定水准比例因子为0.1、0.01、0.001、0.0001、0.00001和0.000001共6个不同值,对反褶积后格林函数的振幅信噪比、格林函数相对于反褶积前波形的走时差及两者的互相关系数峰值进行比较。振幅信噪比采用有效信号幅值绝对值的最大值与噪声振幅的均方根之比。
表 1为A09工况NJNK台不同水准比例因子得到的格林函数振幅信噪比、走时差和互相关系数峰值,表 2为A13工况NJJS、NJNK台的计算结果。由表 1、2可见,随着水准因子值减小,格林函数的振幅信噪比呈减小趋势;格林函数相对于反褶积处理前波形的走时差有差别,不同的水准比例因子可能引起数毫秒的走时变化;不同工况、不同台站计算的互相关系数峰值变化情况也不同。图 5为A09工况NJNK台不同水准比例因子反褶积后的结果。由图 5可见,水准比例因子越小,背景噪声越大,小到一定值时有效信号则湮没在背景噪声中。因此,在使用频率域水准反褶积方法时,需要根据实际情况选取合适的水准比例因子。由图 5还可见,反褶积后的波形相对反褶积前有一个较为明显的走时变化,约为0.3s,其原因可能是,气枪激发信号主要由气枪气体释放所产生的压力脉冲和由于气泡在水中的振荡所产生的气泡脉冲构成,压力脉冲属于高频信号,主要频率约为数十到数百赫兹,衰减较快,远场测震台站几乎无法记录到压力脉冲;而气泡脉冲则属于低频信号,主要频率为3~8Hz,远场测震台站记录到的主要是气泡脉冲传播引起的地面振动,根据水库气枪浮台下方库底OBS的记录以及气枪上方2m处水听器的记录,气泡脉冲约在压力脉冲后0.2s左右产生,同时,由于进行本次气枪实验时,浮台距岸边的测震仪相对较远,约200m,因此,测震仪的记录并不能完全等效于震源时间函数。根据浮台与岸边测震仪的记录,及波在水中的传播速度(1.5km/s,由于气枪与岸边测震台站间距离仅200m,因此,我们认为波在水中或地表较浅的上层传播)可知,气枪激发产生的压力脉冲传播至岸边测震台约需0.1s,气泡脉冲则需0.3s左右,即本文中利用震中距为200m的岸边测震记录作为近似震源时间函数时,本身就引入了0.3s左右的时间误差,这可能是本研究反褶积计算后波形走时出现0.3s变化的主要原因。这也说明,将距气枪震源200m的台站记录作为震源时间函数可能并不完全适用。但由于本研究均使用同一台站的观测数据,因此,并不影响本文后续分析结论。
| 表 1 A09工况NJNK台不同水准比例因子格林函数振幅信噪比、走时差和互相关系数峰值比较 |
| 表 2 A13工况NJJS与NJNK台不同水准比例因子格林函数振幅信噪比、走时差和互相关系数峰值比较 |

|
图 5 A09工况NJNK台不同水准比例因子反褶积后的结果 |
在使用频率域水准反褶积方法监测地壳介质变化前,有必要了解反褶积计算结果的影响因素。本文采用仿真数值模拟方法,通过改变远场台或参考台的背景噪声水平以及不同水准比例因子,探讨背景噪声对反褶积计算的影响。
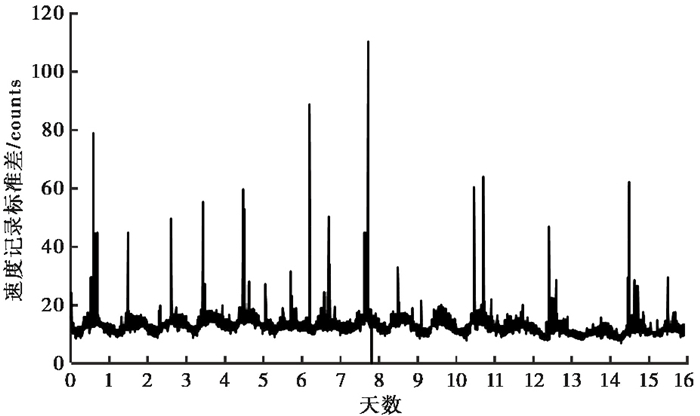
以往研究中,多采用随机白噪声数值来模拟噪声的变化,而实际上,地震仪记录的天然噪声并不是绝对的随机白噪声,而是随时间、空间具有一定变化规律的噪声,因此,本文选取气枪未激发时段连续半个月测震台站记录的噪声数据,以仿真噪声变化对分析结果的影响。对所选噪声数据每隔10min抽取一段,并作基线校正、2~8Hz滤波和两头尖灭处理,再计算每段噪声的标准偏差,结果如图 6所示,由图 6可见,噪声呈规律性日变化。
|
图 6 噪声日变化 |
计算步骤如下:①把远场台记录数据预处理后的噪声部分置换为零,再将抽取的噪声加到该台的气枪记录上,将生成的新信号当作远场台记录;②把新的远场台记录与参考台记录做反褶积得到近似格林函数(根据前文所述,水准比例因子取0.001);③由于反褶积会引入高频噪声,因此需要再次滤波,频带范围为2.5~6Hz;④采用互相关时延方法,计算根据不同水准比例因子得到的近似格林函数P波段(0.5s窗长)走时误差随噪声的日变化;⑤改变远场台记录的信噪比,即改变抽取噪声的幅值,计算格林函数走时误差随噪声的日变化;⑥对参考台按照同样的流程进行处理。
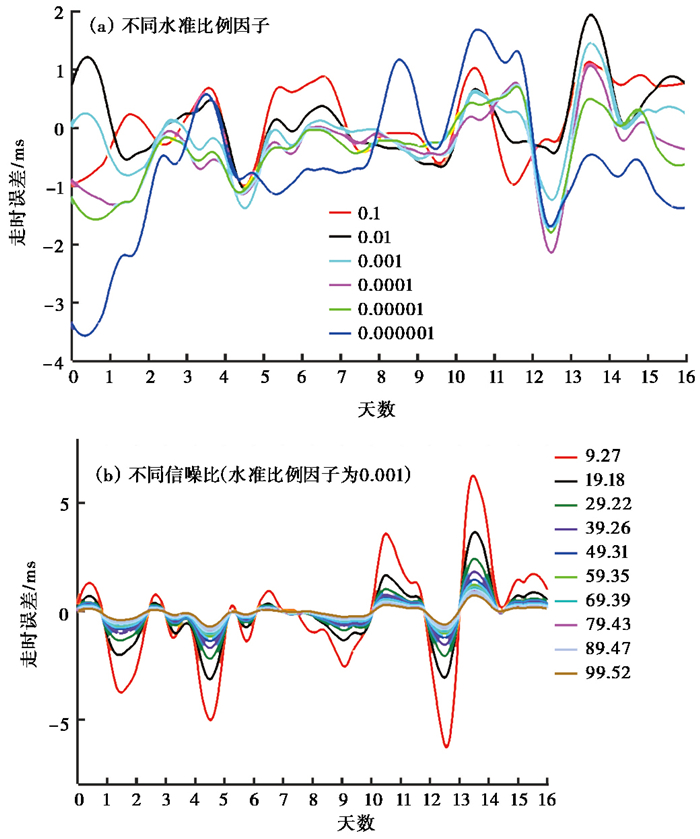
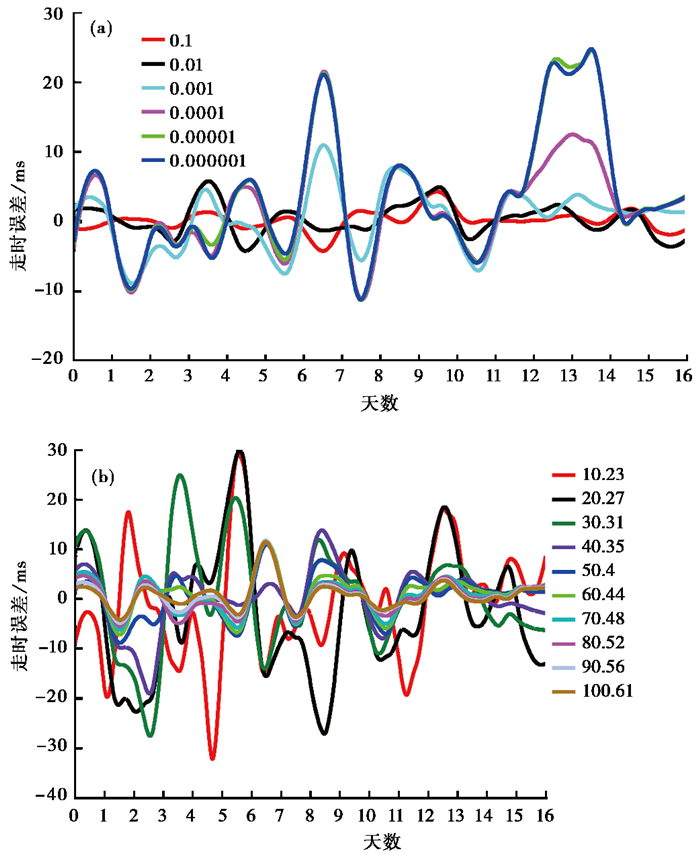
图 7、8分别为A09工况远场台NJNK和参考台L3583加噪声反褶积后格林函数P波段走时识别误差随噪声的日变化。图 7(a)为远场台气枪记录的信噪比约为49时不同水准比例因子的计算结果,图 8(a)为参考台记录的信噪比约为50时不同水准比例因子的结果,由图 7(a)、8(a)可见,当因子相同,且远场台、参考台记录的信噪比相差不多时,前者计算的走时误差只有数毫秒,而后者识别的走时误差明显大于前者,可见参考台记录的信噪比对结果的影响远大于远场台;另外,水准比例因子的不同对反褶积计算后波形的走时有影响,当水准比例因子取值过小时,走时误差较大。本研究只是改变台站的背景噪声水平,并未更改气枪信号,因此,不同信噪比的气枪记录反褶积计算后波形的走时变化理论上应该相同,但结果显示,由不同的信噪比计算得到的走时变化并不相同(图 7(b)、8(b)),这说明台站的背景噪声水平对结果有较大影响,气枪记录的信噪比越大,所得结果精度越高。远场台不同信噪比的气枪记录所得走时误差变化趋势一致,说明识别误差均由噪声引起,这就要求在正式的应用中需要花费较大精力去排除噪声影响。当远场台记录的信噪比大于10时,走时误差一般小于6ms。对参考台具有不同信噪比的记录,由于信噪比不同会影响反褶积中的近似震源函数,因此得到的走时误差变化趋势一致性较差。此外,参考台记录的信噪比对走时识别结果影响更大,信噪比为30左右的参考台记录,走时误差可能达到20ms左右,即使对于信噪比100左右的参考台记录,走时误差也可能达到几毫秒。此外,不同水准比例因子及台站记录的信噪比计算的走时误差日变化与背景噪声日变化间没有明显关联。
|
图 7 远场台加噪声反褶积后P波段走时误差随噪声的日变化 |
|
图 8 参考台加噪声反褶积后P波段走时误差随噪声的日变化 (a)不同水准比例因子;(b)不同信噪比(水准比例因子为0.001) |
为了检验利用频率域水准比例因子反褶积方法消除气枪震源影响的效果,我们对工作压力为1000、1200、1500、1800、2000psi时NJNK测震台记录进行反褶积计算(水准比例因子取0.001),以枪压为1000psi的A09工况作为参考,比较不同枪压激发的观测记录反褶积前后波形的时间延迟。
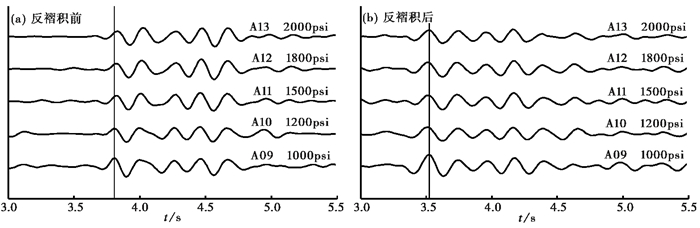
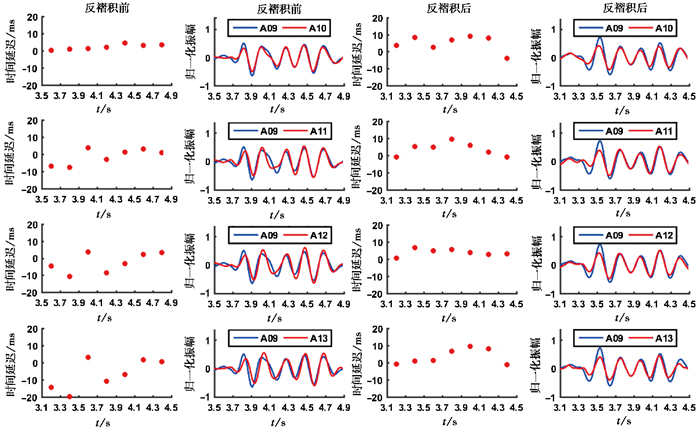
图 9(a)、9(b)分别为不同工作压力的气枪激发信号反褶积前后的波形。由于气枪震源信号重复性较高,因此以竖线为参照,比较各波形初始震相波段内峰值的到时位置。由图 9可见,随着枪压的增加,反褶积前波形峰值位置的到时存在一定差异,且枪压为2000psi时较明显,而经反褶积计算后,波形峰值位置的到时差异变小。设时间窗长为0.3s,步长为0.2s,计算不同枪压的激发信号在反褶积前后分别与A09工况不同波段间的互相关时间延迟(图 10)。A9、A10工况的枪压差为200psi,反褶积前两列波形不同波段的时间延迟较小,反褶积后时间延迟稍大,但都小于0.01s(即1个采样点);反褶积前后初始震相波段计算的应为第2个时间窗,该波段算得的时间延迟为时间延迟图中第2个圆点,反褶积后的时间延迟基本比反褶积前小,特别是较A09工况而言,A13工况反褶积前时间延迟达2个采样点,经反褶积后时间延迟显著缩短。由此可见,利用频率域水准反褶积方法,可以有效消除震源差别较大的影响。
|
图 9 不同工作压力的气枪信号反褶积前后波形对比 |
|
图 10 NJNK台不同枪压气枪信号相对A09反褶积前后波形的时间延迟 |
本文以2016年福建南一水库气枪实验资料为研究对象,通过分析水准比例因子及台站背景噪声对反褶积结果的影响,研究利用反褶积法消除震源影响的效果,得出以下结论与认识。
(1) 水准比例因子影响反褶积后波形的信噪比及走时,水准比例因子越小,反褶积后波形的信噪比越小,当水准比例因子取值过小时,走时识别误差较大。实际应用时,需进行分析后选取合适的水准比例因子。
(2) 台站的背景噪声对反褶积计算结果有影响。气枪记录的信噪比越大,走时识别精度越高,参考台记录的信噪比对结果的影响远大于远场台;当远场台记录的信噪比大于10时,走时误差一般小于6ms;当参考台记录的信噪比为30左右时,走时误差可能达到20ms左右,即使对于信噪比100左右的参考台数据,走时误差也可能达几毫秒。
(3) 利用频域水准比例因子反褶积方法,可以消除不同工作压力引起的震源影响,验证了该方法去除震源效应的有效性。该方法在震源差异较大时去除震源效应的效果较好,在震源差异较小时,反而可能引入方法误差。
本文对频域水准反褶积计算结果的影响因素及反褶积法消除震源影响的效果进行了初步分析,研究结果可为反褶积方法应用于气枪监测地壳介质变化中的应用提供参考。
| 陈颙, 王宝善. 2016, 前言. 中国地震, 32(2): 165–167. |
| 刘自凤, 苏有锦, 王宝善, 等. 2015, 宾川主动源地震波走时变化分析方法研究. 地震研究, 38(4): 591–597. |
| 栾奕, 杨宏峰, 王宝善. 2016, 大容量气枪主动源波形资料处理(一):云南宾川. 中国地震, 32(2): 305–318. |
| 王宝善, 葛洪魁, 王彬, 等. 2016, 利用人工重复震源进行地下介质结构及其变化研究的探索和进展. 中国地震, 32(2): 168–179. |
| 王宝善, 杨微, 王伟涛, 等. 2012, 利用反褶积消除激发环境对水库大容量气枪信号的影响.见:中国地球物理学会, 中国地球物理第二十八届年会摘要文集. 北京: 中国学术期刊(光盘版)电子杂志社. |
| 魏芸芸, 王海涛, 苏金波, 等. 2016, 新疆2次中强地震前气枪震源反射波震相走时异常变化初步研究. 中国地震, 32(2): 270–281. |
| 翟秋实, 姚华建, 王宝善. 2016, 气枪震源资料反褶积方法及处理流程研究. 中国地震, 32(2): 295–304. |
| Céspedes I, Huang Y, Ophir J, et al. 1995, Methods for estimation of subsample time delays of digitized echo signals. Ultrason Imaging, 17(2): 142–171. DOI:10.1177/016173469501700204. |
| Helmberger D, Wiggins R A. 1971, Upper mantle structure of midwestern United States. J Geophys Res, 76(14): 3229–3245. DOI:10.1029/JB076i014p03229. |