气枪震源水中能量辐射特性研究
董明荣, 符力耘, 邢超, 杨军, 李孝宾
中国地震  2018, Vol. 34 2018, Vol. 34 Issue (1): 25-34 Issue (1): 25-34
|
在主动源探测(陈颙等,2005;王彬等,2015;王宝善等,2016)过程中,需要气枪震源长期多次重复激发产生地震波。气枪激发后先是高压气体把能量传递到水里,然后水与水底进行能量传递,产生地震波。这2个传递过程都存在能量消耗,不能100%传递。在水中爆炸能量辐射的评估及其与地震关系方面,已有一些关于炸药震源当量与地震震级间关系的研究(Savage et al,2001;宋浦等,2008;杨振等,2015),但关于气枪震源在水体里能量辐射特性的研究还较少。Ronen(2002)假设冲击波和气泡脉动都是球面波,对Caldwelle等(2000)文中的水中子波信号进行了冲击波和气泡脉动能量的计算。
气枪是脉冲震源,在水中激发的机理与炸药在水中爆炸的机理相似。炸药的水中爆炸在军事等领域有重要应用,已开展了一些理论和实验研究工作(汪斌等,2008;张阿漫等,2008)。Cole(1948)提出了TNT炸药水中爆炸气泡脉动周期和最大半径的经验公式,郅斌伟等(2009)对于TNT当量1217.6kg的炸药水中爆炸采用类似Cole(1948)的经验公式、PAMFLOW软件和基于JWL状态方程的气泡计算程序进行了气泡周期和半径的计算,马坤等(2015)开展了不同水深的0.125、0.5、1g TNT当量药球爆炸实验,对Cole(1948)的经验公式系数进行了修正。这些研究表明,Cole(1948)的经验公式对从克量级到千克量级的TNT当量炸药水中爆炸都适用。另外,也有一些使用AUTODYN、DYTRAN、ABAQUS等商业软件或者采用自编程序进行炸药水中爆炸的模拟研究(张志江等,2007;贾宪振等,2015)。相对于运算量大、计算耗时多的数值模拟,上述实验总结出的经验公式有运算量小、节约计算时间、便于分析规律性等优点。本文综合了水中爆炸相关理论和经验公式,研究气枪震源水中能量辐射的规律,以期为主动源探测气枪震源的理论研究和优化使用等提供参考。
1 气枪震源水中能量辐射特性计算原理已开展的气枪震源激发实验过程中,获取的与能量计算相关的数据有供气压力、冲击波幅度、第1个气泡幅度、第1个气泡的周期等。气枪和炸药在水中激发都是瞬间膨胀源,故可以参考水中炸药爆炸的计算方法来计算气枪震源的激发特性。大多数关于水中炸药爆炸的计算公式都是经验公式,因此,本文侧重于分析数据变化的规律。
气枪震源的动力来源于高压气体,气枪辐射的初始能量可以根据高压气体的容量和压力计算(Ronen,2002),即
| $ {E_0} = P \cdot V\ln \left({P/{P_{{\rm{atm}}}}} \right) $ | (1) |
式中,E0为释放的能量(J);V为高压气体的容量(inch3);P为气枪的工作压力(psi);Patm为水面上的环境气压(psi)。另,容量和压力单位inch3、psi可以转化为m3、Pa。
E0是气枪震源向水中辐射的总能量,包含了冲击波能、气泡能,以及辐射过程中的热能等能量损耗。E0的单位为J,TNT炸药的爆热为4.2×106J/kg,则气枪辐射能量可以换算为TNT当量(kg),即
| $ {W_0} = {E_0}/4.2 \times {10^6} $ | (2) |
设气枪震源辐射到水中的能量为E,则气枪震源水中能量辐射效率η为
| $ \eta = \frac{E}{{{E_0}}} \times 100\% $ | (3) |
根据声能相关理论(杜功焕等,2001),忽略气枪震源在水中激发的冲击波和气泡脉动波的指向性,假设这2种波都为球面波,那么根据水中距气枪震源为R的水听器接收的压力p以及波动周期T可以计算出气枪震源辐射到水中的能量Ep,即
| $ {E_p} = 4{\rm{ \mathsf{ π} }}{R^2} \cdot \frac{{{p^2}}}{{\rho C}} \cdot T $ | (4) |
式中,C为水中声速(m/s),在常温下取1460m/s;ρ为水的密度(kg/m3),取1000kg/m3。
把气枪震源辐射冲击波压力ps和周期Ts代入式(4)计算出冲击波能Eps,代入式(3)可计算出冲击波能的能量辐射效率ηs。把气枪震源辐射气泡幅度pb和周期Tb代入式(4)计算出气泡能Epb,代入式(3)可计算出气泡能的能量辐射效率ηb。这2个辐射效率之和ηsb为气枪震源水中能量辐射效率。气枪震源实际的水中能量辐射是有指向性的,因此,该能量辐射效率计算值偏大。
水中爆炸冲击波能Esi的积分计算公式(ANSYS Corporation,2005)为
| $ {E_{{\rm{si}}}} = \frac{{4{\rm{ \mathsf{ π} }}{R^2}}}{{\rho C}}\int_0^{6.7\theta } {{p^2}} \left(t \right){\rm{d}}t $ | (5) |
式中,R为测点到爆心的距离(m);p(t)为距爆心R处t时刻的冲击波压力(Pa);C为水中声速(m/s);θ为时间衰减常数(s),即压力峰值从冲击波压力峰值pm衰减到pm/e所需的时间。
TNT炸药在无限水域中的水中爆炸,气泡脉动周期Tb和最大半径Rmax的经验公式(Cole,1948)为
| $ {T_{\rm{b}}} = 2.064\frac{{E_1^{1/3}}}{{{{\left({h + 10} \right)}^{5/6}}}} $ | (6) |
| $ {T_{{\rm{max}}}} = 3.3825{\left({\frac{{{W_1}}}{{h + 10}}} \right)^{1/3}} $ | (7) |
式中,W1为等效装药量,即TNT当量(kg);h为水中爆炸的深度(m),本文h为气枪的沉放深度。根据气枪震源的第1个气泡的脉动周期Tb,从式(6)可以得到气枪震源的TNT当量W1为
| $ {W_1} = {\left[ {\frac{{{T_{\rm{b}}}{{\left({h + 10} \right)}^{5/6}}}}{{2.064}}} \right]^3} $ | (8) |
W1、W0都是气枪震源的初始TNT当量,理论上应该相等,但由于材料性质不同等原因,使得气枪震源与TNT炸药产生相同的水中爆炸脉动频率所需的初始能量不同,这反映了气枪震源相对于TNT炸药的能量辐射效率的高低。设u为气枪震源的高压气体在水中的气泡频率系数,其数值是由气枪震源的水中子波计算的W1与高压气体初始能量W0的比值,反映了随气泡周期和频率变化而变化的气枪震源的高压气体能量释放到水中的能量辐射效率。u越大,气枪震源水中的能量辐射效率越高。
定义u的计算公式为
| $ u = {W_1}/{W_0} $ | (9) |
水中脉动气泡尺寸越大表明能量越大,在气枪震源实际工程应用中对于该气泡半径的测量较困难。由于材料性质不同等原因,粗略估计,相同TNT当量的气枪震源比TNT炸药产生水中爆炸脉动气泡的半径要小。取气枪震源的初始TNT当量为W1,增加气泡半径系数α(0<α<1),则气枪震源气泡脉动最大半径Rmax1为
| $ {R_{\max 1}} = 3.3825{\left({\frac{{\alpha {W_1}}}{{h + 10}}} \right)^{1/3}} $ | (10) |
取气枪震源的初始TNT当量为W0,则气枪震源气泡脉动最大半径Rmax0为
| $ {R_{\max 0}} = 3.3825{\left( {\frac{{\alpha {W_0}}}{{h + 10}}} \right)^{1/3}} $ | (11) |
在云南省大理白族自治州宾川县大银甸水库的气枪震源基地(图 1)开展了水听器观测气枪震源激发子波的实验。由图 1可见,一个"口"字形浮台每边中央下10m水深处各悬挂了1支气枪,共4支,岸上的塔吊用于吊运气枪等实验设备和器材。使用的气枪是美国Bolt公司的Bolt1500LL气枪(图 2),该气枪的气室容量约0.0328m3,气室压力调整范围6~15MPa。使用丹麦B & K公司的B & K8105水听器进行水中子波观测,使用美国NI公司的NI USB6251采集卡进行AD转换。

|
图 1 宾川县大银甸水库的气枪震源基地 |

|
图 2 Bolt1500LL气枪 |
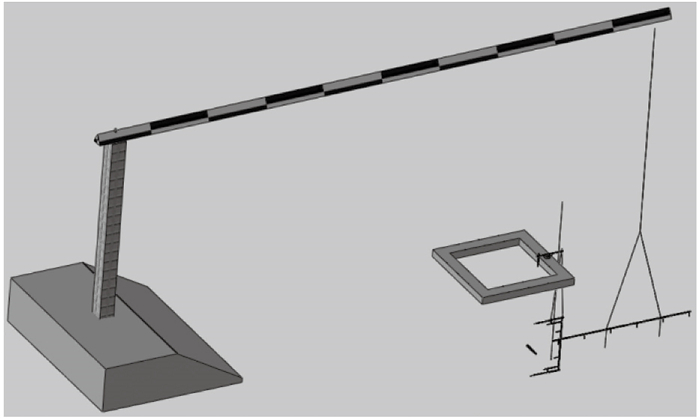
气枪激发后几米范围内水体涌动幅度较大,因此,设计、加工了约18m长的直线形测试架和直径6m的半圆形测试架沉放到与气枪等深度处(图 3),在测试架上安装水听器进行实验,这2个测试架不同时使用。测试架的约束能提高水听器相对于气枪的布设精度,还能减小水体涌动时水听器的运动。计算能量辐射效率的水听器数据是气枪激发产生的短时信号,该信号接收时水体涌动较小,可视为水听器保持静止。
|
图 3 实验布局示意图 |
开展了不同供气压力、枪数的实验,数据采样率为100kHz,选取了3个测点的数据进行能量辐射特性的计算。气枪枪体中轴线在水平面上,测点1在气枪正下方的3m处,水听器安装在半圆形测试架上。测点2在气枪中轴线的水平面上垂线的3m处,水听器安装在半圆形测试架上。测点1、2在同一个垂面内。测点3在气枪中轴线的延长线的3m处,水听器安装在直线形测试架上。
3 气枪震源水中能量辐射特性计算图 4为1支气枪激发时,气枪正下方3m处测点1的B & K8105水听器观测到的供气压力为15、6MPa的震源子波。1支气枪的气室容量为0.0328m3,气泡半径系数α取0.25,能量辐射特性计算结果见表 1。计算过程中脉冲持续时间、气泡周期和幅度等都由程序自动提取和计算,以避免人工读取波形数据带来的误差。由表 1可见,供气压力为15MPa时,气枪震源激发能量为2537434J,相当于0.25级的地震;供气压力为6MPa时,气枪震源激发能量为834790J,相当于0.05级的地震。供气压力为15MPa和6MPa时,球面波假设计算的Eps是积分计算的Esi的3.6和17.0倍,表明根据Eps和Epb计算的能量辐射效率是气枪震源水中能量辐射效率的上限(Ronen,2002)。气泡半径Rmax1比Rmax0略大,Rmax1是根据水中观测数据计算的,更能反映水中的特性,因此,主要对Rmax1进行分析,并取Rmax=Rmax1。

|
图 4 测点1供气压力为15MPa(a)、6MPa(b)时的气枪震源子波 |
| 表 1 测点1供气压力为15、6MPa时气枪震源子波能量辐射特性计算结果 |
图 5为1支气枪激发时测点1、2不同供气压力的能量辐射效率计算结果。由图 5可见:①气泡能辐射效率随着供气压力的增加而增大;②冲击波能辐射效率随着供气压力的增加先增大后减小;③气枪震源垂直向下的能量辐射效率高于水平方向的能量辐射效率;④随着供气压力的增大,气泡能辐射效率会超过冲击波能辐射效率;⑤供气压力为15MPa时,气枪震源垂直向下的能量辐射效率为9.4%。

|
图 5 测点1(a)、测点2(b)不同供气压力的能量辐射效率 |
气枪激发的气泡脉动是具有多个周期的阻尼振荡,持续时间较长,辐射效率随供气压力的增加而增大,垂直向下的能量辐射效率高于水平方向的能量辐射效率,因此,气枪激发后引起地震的主要能量是垂直向下的气泡能。
气枪震源也是射流声源的一种,但可参考的声效率计算结果鲜见报道,目前仅有Ronen(2002)粗略计算的水中气枪阵列震源约25%的声效率数据。周帆等(2012)通过实验数据计算了火箭发动机在空气中的射流噪声的声效率为0.51%。水中声效率通常大于空气中的声效率,而且气枪激发的水中气泡脉动是效率较高的能量辐射过程,因此,本文计算的气枪震源水中声效率最大值9.4%虽然偏大,但基本是合理的。
图 6为测点3不同供气压力、枪数的能量辐射效率计算结果。由图 6可见:① 1支枪的气泡能和冲击波能辐射效率随着供气压力的增加先增大后减小;②冲击波能辐射效率大于气泡能辐射效率;③ 1支枪的气枪震源能量辐射效率约1.9%。

|
图 6 测点3不同供气压力、枪数的能量辐射效率 |
由于这4支气枪在边长7m的正方形的4条边上,水听器测点在其中一条边上,接收到的其余各支气枪的震源子波的传播距离不是3m,而且这4支枪在该测点处的叠加情况复杂,因此,本文的能量辐射特性主要分析1支枪的情况。
图 7为测点3不同供气压力、枪数的首次膨胀气泡的最大半径计算结果,其中,2支枪和4支枪的是等效气泡半径,即把多个气泡的联合作用效果当作1个气泡的计算结果,气泡半径越大,则能量越大。由图 7可见:①气泡半径随着供气压力的增加而增大。②供气压力小于12MPa时,1支枪和2支枪的气泡半径类似,4支枪的明显比1支枪、2支枪的大,表明水平传播8m的气枪震源压力波已经近似各自独立,互相的影响较小,叠加增强效果较弱;供气压力大于12MPa后,2支枪比1支枪的气泡半径大,而且差值随压力的增加而增大。4支枪时水听器与最近的2支枪间距为3~5m,因此,水平传播5m的气枪震源压力波可以叠加增强。③气枪供气压力越大,气枪震源压力波叠加增强的距离越远,在相同距离处的叠加效果越明显。

|
图 7 由测点3水听器信号计算的气泡半径 |
图 8的"垂面"和"水平面"曲线分别为测点1、2处B & K8105水听器信号的首次膨胀气泡的最大半径计算结果。由图 8可见,这2条曲线基本重合。首次膨胀气泡的最大半径由气枪沉放深度h和W1决定,W1代表了气枪向水中辐射的能量。实验过程中气枪沉放深度不变,因此,这2条曲线基本重合表明不同供气压力的气枪水平方向和垂直下方的能量辐射基本相同。

|
图 8 由测点1、2水听器信号计算的气泡半径 |
图 9为气枪震源水下激发时的照片。气枪深度为10m,连接气枪的铁链约2m,铁链悬挂在1个边长约7m的水平架子下方,摄像机沉放深度7m,因此,摄像机距架子约1m,距气枪约3m。悬挂气枪的架子正对摄像机的钢材宽度约0.1m。图 9水下激发时刻大约为首次膨胀气泡半径最大的时候,该气泡最大半径约对应3个架子的宽度,因此,按照三角形的比例关系可知,气泡的半径为9倍的架子宽度,即9×0.1=0.9m,与前面的计算结果0.89m较接近。这也是本文气泡半径系数α取0.25的原因。

|
图 9 气枪震源激发照片 |
图 10(a)为测点3不同供气压力、枪数的气泡频率系数计算结果。由图 10(a)可见,1支枪的气泡频率系数明显大于2枪和4枪的,本文的气泡频率系数主要分析1支枪。图 10(b)是为1支枪时不同供气压力的3个测点气泡频率系数计算结果。由图 10(b)可见,3条曲线的数值接近,测点1、2、3的均值依次是2.31、2.42、2.37,3条曲线的均值为2.36。因此,可以取气枪震源的高压气体水中的气泡频率系数为2.36,即1 kgTNT当量的气枪震源与2.36kg的TNT炸药产生的水中爆炸的气泡脉动频率相同。

|
图 10 测点3(a)和3个测点(b)的气泡频率系数 |
目前,气枪震源子波计算大多是以自由气泡振荡理论为基础开展的理论模拟,由其可以得到气枪激发的气泡脉动周期,但探讨气枪激发气泡半径计算的研究很少,而且通过实验数据总结的计算气枪激发气泡脉动周期和最大半径的经验公式不多,如陈浩林等(2003)探讨了以自由气泡振荡理论为基础的国际上主要的几种气枪单枪理论模型并给出了气枪子波的模拟方法,李绪宣等(2012)利用PGS公司研发的基于气泡自由振荡理论的Nucleus软件进行了气枪震源子波的数值模拟。
本文以实验数据为基础,通过对水中炸药爆炸经验公式的修正得到了计算气枪震源水中激发气泡脉动周期和最大半径的经验公式,即在水中炸药爆炸的经验公式中增加气泡频率系数2.36和气泡半径系数0.25,以气枪震源的高压气体TNT当量为输入参数,对于气泡半径Rmax,系数为0.25×2.36=0.59,由此得到1支气枪震源水中激发的气泡脉动周期Tb和最大半径Rmax的经验公式为
| $ {T_{\rm{b}}} = 2.064\frac{{{{\left({2.36{W_0}} \right)}^{1/3}}}}{{{{\left({h + 10} \right)}^{5/6}}}} $ | (12) |
| $ {R_{{\rm{max}}}} = 3.3825{\left({\frac{{0.59{W_0}}}{{h + 10}}} \right)^{1/3}} $ | (13) |
以供气压力为15MPa的1支气枪在水深10m处激发为例,由水听器子波数据计算的该气泡的周期为0.1926s,由水下摄像数据计算的该气泡的半径约为0.9m。该气枪的高压气体TNT当量W0为0.6kg,那么,由式(12)、(13)可以计算出气泡周期为0.1909s,气泡半径为0.88m。
4 结论根据气枪震源水中子波数据计算了气枪震源向水中释放高压气体的能量辐射效率和气泡半径,通过在水中炸药爆炸的经验公式中增加气泡频率系数和气泡半径系数,得到了用于计算气枪震源水中激发气泡脉动的周期和最大半径的经验公式。结果表明:①垂直向下的能量辐射效率高于水平方向的能量辐射效率;②气枪激发后引起地震的主要能量是垂直向下的气泡能;③冲击波能辐射效率随着供气压力的增加先增大后减小;④垂直向下的气泡能辐射效率随着供气压力的增加而增大,随着供气压力的增加,垂直向下的气泡能辐射效率会超过冲击波能辐射效率;⑤供气压力为15MPa时,气枪震源垂直向下的能量辐射效率为9.4%;⑥各方向的能量辐射效率不同,表明气枪震源辐射的冲击波和气泡脉动波不是球面波;⑦气枪供气压力越大,气枪震源压力波叠加增强的距离越远,在相同距离处的叠加效果越明显,不同供气压力的气枪的水平方向和垂直下方的能量辐射基本相同。本文的研究结果可以为主动源探测的气枪震源理论研究、优化使用、节能减排以及水中结构的抗震防护等提供参考。
致谢: 在本文研究过程中,得到了中国地震局地球物理研究所、云南省地震局、中国地震局滇西地震预报实验场等多家单位的大力支持与帮助,还得到了王永涛、叶泵、宋志峰、卢晓林、毛德培、卜维生、董娟等同事的帮助,在此表示衷心感谢。| 陈浩林, 宁书年, 熊金良, 等. 2003, 气枪阵列子波数值模拟. 石油地球物理勘探, 38(4): 363–368. |
| 陈颙, 朱日祥. 2005, 设立"地下明灯研究计划"的建议. 地球科学进展, 20(5): 485–489. |
| 杜功焕, 朱哲民, 龚秀芬. 2001, 声学基础(第2版). 南京: 南京大学出版社. |
| 贾宪振, 南海, 王晓峰, 等. 2015, 有氧化剂(AP)含铝炸药水中爆炸数值模拟. 科学技术与工程, 15(6): 1–4. |
| 李绪宣, 王建花, 杨凯, 等. 2012, 海上深水区气枪震源阵列优化组合研究与应用. 中国海上油气, 24(3): 1–6. |
| 马坤, 初哲, 王可慧, 等. 2015, 小当量炸药深水爆炸气泡脉动模拟实验. 爆炸与冲击, 35(3): 320–325. DOI:10.11883/1001-1455-(2015)03-0320-06 |
| 宋浦, 肖川, 梁安定, 等. 2008, 炸药空中与水中爆炸冲击波超压的换算关系. 火炸药学报, 31(4): 10–13. |
| 王宝善, 葛洪魁, 王彬, 等. 2016, 利用人工重复震源进行地下介质结构及其变化研究的探索和进展. 中国地震, 32(2): 168–179. |
| 王彬, 吴国华, 苏有锦, 等. 2015, 宾川地震信号发射台的选址、建设及初步观测结果. 地震研究, 38(1): 1–6. |
| 汪斌, 张远平, 王彦平. 2008, 水中爆炸气泡脉动现象的实验研究. 爆炸与冲击, 28(6): 572–576. DOI:10.11883/1001-1455(2008)06-0572-05 |
| 杨振, 沈晓乐. 2015, 爆破战斗部水中兵器爆炸威力评定方法研究. 爆破, 32(2): 51–53. |
| 张阿漫, 姚熊亮. 2008, 近边界三维水下爆炸气泡动态特性研究. 爆炸与冲击, 28(2): 124–130. DOI:10.11883/1001-1455(2008)02-0124-07 |
| 张志江, 徐更光, 王廷增. 2007, 炸药水中爆炸气泡脉动分析计算. 爆破, 24(1): 17–20. |
| 郅斌伟, 马硕, 张志江. 2009, 水底爆炸气泡脉动特性. 爆破, 26(3): 22–24. |
| 周帆, 姜毅, 张学文, 等. 2012, 火箭发动机射流复杂噪声测量数据时频分析. 弹箭与制导学报, 32(3): 145–147. |
| ANSYS Corporation. 2005, Autodyn theory manual. 6.1. United States: Century Dynamics |
| Caldwell J, Dragoset W. 2000, A brief overview of seismic airgun arrays. Leading Edge, 19(8): 898–902. DOI:10.1190/1.1438744. |
| Cole R H. 1948, Underwater explosion. Princeton: Princeton University Press |
| Ronen S. 2002, Psi.pascal, bars, and decibels. Leading Edge, 21(1): 60–61. |
| Savage B, Helmberger D V. 2001, Kursk explosion. Bull Seismol Soc Am, 91(4): 753–759. DOI:10.1785/0120000295. |