地震目录是地震活动性研究和地震危险性分析的重要资料。现代仪器记录地震目录的历史只有几十年,虽然基于历史文献记载和古地震研究可以将地震目录时间延伸,但仍不足以研究复发周期长、概率小的大地震事件,无论是基于统计学方法来重现周期长达百年的地震预测或地震区划研究,还是对基于一定物理模型假设的地震前兆或预测模型进行检验和修正,都是不够的(周仕勇,2008)。因此,开展地震目录模拟研究具有重要意义。
人工地震目录模拟已有数十年的发展历史,可采用基于力学实验或数值模拟、统计学,以及力学与统计模型相结合等方法进行。Mogi(1962)通过岩石破裂力学实验,记录实验过程中微观破裂事件产生的声发射,依据微破裂事件序列方法模拟地震目录,并根据破裂事件(可包含多个“前震”或“余震”)序列,研究了主震型、前震-主震-余震型和群震型地震的破裂过程(唐春安,1997;唐春安等,1997)。这些模拟结果对于研究地震孕育、发生的成因机理具有重要启示,但无法模拟由一系列独立地震事件组成的长地震序列目录。
基于力学与统计模型相结合的地震目录模拟,建立在地震孕育发生机制理论模型(Sólnes et al,1997;石耀霖等,1998;Console et al,2016;Zhou et al,2016)假设的基础上,如基本的弹簧-滑块模型(Burridge et al,1967)或改进的弹簧-滑块-阻尼器模型(朱元清等,1991),以及在此基础上建立的断层(相互作用)系统地震活动模型(金欣等,2017;周仕勇,2008)。以这些力学模型所反映的应力-应变过程为基础,结合细胞自动机模型(刘桂萍等,1995、2000)、耦合应力释放统计模型(AIC)(李红等,2015)、布朗时间过程模型(BPT模型)、时间可预报模型或基于经验的模型(Working Group on California Earthquake Probabilities,2003;Hainzl et al,2007)、EEPAS模型(Rhoades et al,2011;毕金孟等,2017)等,可实现对地震目录的模拟。弹簧-滑块模型或断层系统模型具有比较明确的物理含义和较为严格的理论基础,但因影响地震发生的因素较多,模型参数的设置与实际断裂构造间存在一定差异,模型越复杂,假设条件就越多,这造成模拟的地震目录不确定性较大,模拟结果的检验存在一定的困难(李红等,2015)。
基于统计学的地震目录模拟方法主要依据地震活动的概率分布特点,采用随机实验方法模拟地震目录,如泊松模型(赵宏等,2015)、对数正态模型(Nishenko et al,1987)、韦布尔分布模型(Hagiwara,1974)、伯努利模型(傅征祥等,1995)、ETAS模型(蒋长胜等,2013;徐伟进等,2017)等。这些方法没有直接与地震的成因过程相结合,而是通过结合地震活动期、幕等时间活动特征或成组活动规律、空间丛集以及活动构造块体及其边缘活动等特征,在一定程度上贴近实际地震时空活动规律。
蒙特卡洛方法使用随机抽样技术来实现对物理问题的解决(Huh et al,2016),该方法较逼真地描述了具有随机性质事物的特点及物理实验过程。本文将采用泊松模型,基于蒙特卡洛随机独立重复实验,结合地震震级分布和时间分布规律,模拟区域地震目录,并对生成的目录进行符合性检验,进而以此目录为基础,对研究区未来地震活动危险性进行估计。
1 基于蒙特卡洛随机独立重复实验的地震目录模拟方法蒙特卡洛方法(Monte Carlo method),也称统计模拟方法或随机抽样技术,是以概率和统计理论为基础的数值计算方法。该方法具有对小概率事件处理较好,受几何条件限制小、收敛速度与问题的维数无关等特性,可用于地震、地震灾害分析预测等领域(刘善琪等,2013;廖景高等,2014;Iervolino et al,2016)。近年来,在地震活动性(Ebel et al,1999;Musson,2000;Shaw et al,2007;Yazdani et al,2012;Assatourians et al,2013;Mohammed et al,2014;郭星,2015;郭星等,2016)、地震危险性(Wang et al,2014;Pavel et al,2017;Setiawan,2017)和地震风险评估(Weatherill,2009;Yazdani et al,2012;Bourne et al,2015;刘甲美等,2016)等方面得到应用。
1.1 蒙特卡洛随机独立重复实验方法对于一个给定的物理(或数学)系统,如果系统中某一核心变量s与其概率分布函数F(s)的关系已知,即
| $ F\left(s \right) = r $ | (1) |
函数F(s)为值域[0,1]的单调增函数。通过随机独立抽样确定[0,1]区间均匀随机数r,对式(1)进行反变换,得
| $ s = {F^{ - 1}}\left(r \right) $ | (2) |
即可得到核心变量s的取值。通过多次独立重复抽样,可以确定一系列核心变量值,完成该系统参数的随机模拟实验。上述方法称为反抽样法,是蒙特卡洛随机实验的基本方法之一(Huh et al,2016)。
1.2 指定年限内震级分布确定假定地震的震级分布满足截断的G-R关系(Cornell,1968),则地震震级分布函数F(m)(Youngs et al,1985)为
| $ F\left(m \right) = \left\{ \begin{array}{l} \frac{{1 - {{\rm{e}}^{ - \beta \left({m - {m_0}} \right)}}}}{{1 - {{\rm{e}}^{ - \beta \left({{m_{{\rm{uz}}}} - {m_0}} \right)}}}}, \;\;\;\;{m_0} \le m \le {m_{{\rm{uz}}}}\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他情况 \end{array} \right. $ | (3) |
其中,β=2.3b,b为研究区G-R关系的系数;m0为震级下限,muz为震级上限。F(m)为[0,1]区间的单调增函数,令F(m)=r,对式(3)进行变换,得
| $ m = {m_0} - \ln \left\{ {1 - r * \left[ {1 - {{\rm{e}}^{ - \beta \left({{m_{{\rm{uz}}}} - {m_0}} \right)}}} \right]} \right\}/\beta $ | (4) |
通过产生[0,1]区间的随机数r,确定F(m)的值,再根据式(4)求得地震震级m。
1.3 指定年限内地震数量和相邻两次地震时间间隔确定假定地震活动遵从泊松分布,则对于年平均发生率v0的区域,在[0,t]时间段内发生k次m0级以上地震的概率(潘华等,2013)为
| $ P\left({n = k} \right) = \frac{{{{\left({{v_0} \cdot t} \right)}^k}}}{{k!}} \cdot {{\rm{e}}^{ - {v_0}t}}, k = 1, 2, 3 \cdots $ | (5) |
对式(5)进行求和,得到地震发生次数的概率分布函数为
| $ P\left({n \le k} \right) = \sum\nolimits_{n = 0}^k {P\left({n = k} \right)} = \sum\nolimits_{n = 0}^k {\frac{{{{\left({{v_0} \cdot t} \right)}^k}}}{{k!}}} \cdot {{\rm{e}}^{ - {v_0}t}}, k = 1, 2, 3, \cdots $ | (6) |
通过随机抽样,确定一个[0,1]的随机数作为概率分布函数P(n≤k)的值,根据给定的年发生率v0和时间t,由式(6)运用反抽法就可以确定该时段地震发生的次数k。
由于地震活动服从泊松分布,任意2次地震的时间间隔τj=tj-tj-1则遵循指数分布(胡聿贤,2006),其分布函数为
| $ F\left({{t_j}} \right) = \left\{ \begin{array}{l} 0, \;\;\;\;\;\;\;\;\;\;\;\;\;{t_j} < 0\\ 1 - {{\rm{e}}^{ - {v_0}{t_j}}}, \;\;\;\;{t_j} \ge 0 \end{array} \right. $ | (7) |
仿照反抽法,可以得到地震事件的时间间隔序列,以第1个地震为起点,根据时间间隔tj,即可得到第j次地震事件的发震时间τj。
因此,通过蒙特卡洛随机独立重复实验,依据年发生率v0和b值,可确定区域地震震级分布以及地震事件数量k。在此基础上,针对每次地震事件,确定震级m和发震时间t,得到满足泊松分布假设的模拟地震目录(图 1)。
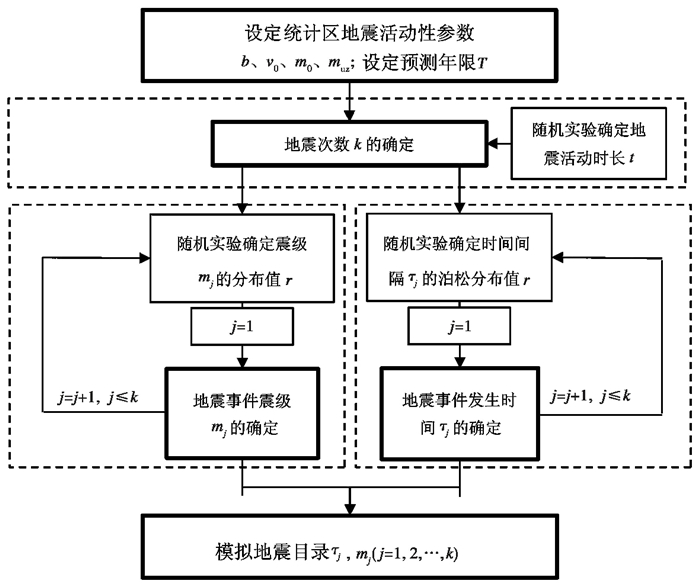
|
图 1 地震目录生成的技术流程 |
汾渭地震带(统计区)位于鄂尔多斯块体东、南缘,南起渭河盆地,北止于怀来-延庆盆地(王继等,2002)。截至2014年,共发生5级以上地震130次,其中,6.0~6.9级地震23次,7.0~7.9级地震7次,8级地震2次(1556年2月2日华县8¼级地震和1303年9月25日洪洞8级地震)。强震主要发生于山西断陷带的忻定盆地、临汾盆地以及渭河断陷带的东部地区(图 2)。第5代地震动参数区划图在收集汾渭地震带地震资料、分析地震活动性特征的基础上,充分考虑了地震资料的不完备性和认识的不确定性,并结合历史地震活动水平与特征(高孟潭,2015;汪素云,1999; 陕西省地震局,2005),确定了汾渭地震带地震活动性参数为b=0.78,v0=2.5,m0=4,muz=8.5(表 1、图 3)。
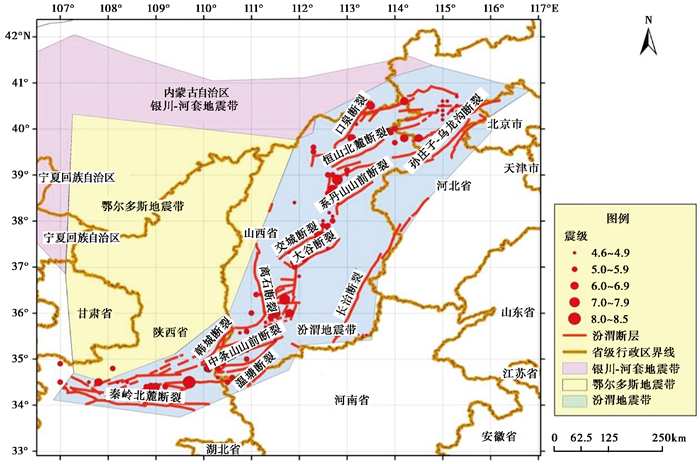
|
图 2 汾渭地震带历史破坏性地震震中分布(公元780~2014年,m≥4.6) |
| 表 1 汾渭地震统计区不同时段的地震年平均发生率 |
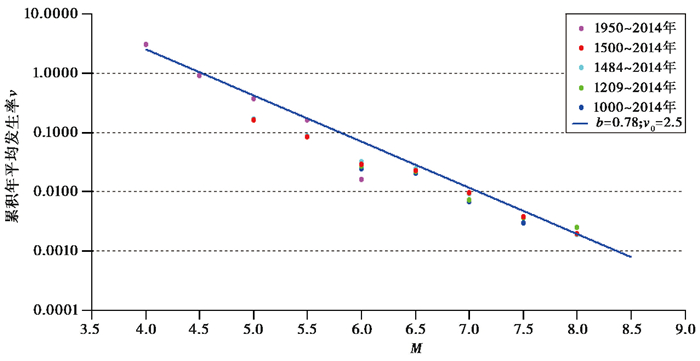
|
图 3 汾渭地震统计区b值及年发生率v0 |
按照前述地震目录模拟方法,模拟汾渭地震带未来30、50、70、100年等不同时间尺度的地震目录。每一时间尺度分别模拟2万组。图 4给出了随机抽取其中6组时间尺度为50年的模拟地震目录的m-t关系。
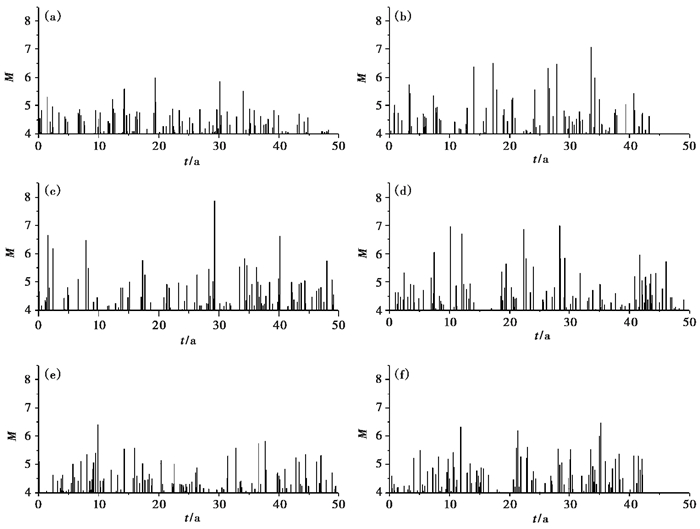
|
图 4 汾渭地震带6组50年模拟地震目录震级-时间关系图 |
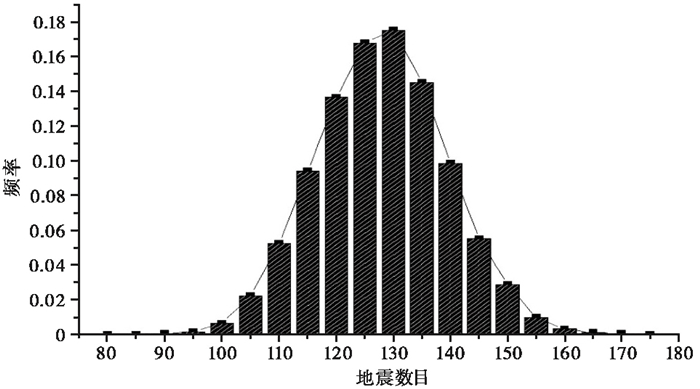
统计2万组50年模拟地震目录的4级以上地震数目,其均值约为125,与理论值125(v0×T))非常接近。以10为间隔,统计其频率分布,结果如图 5所示。由图 5可见,峰值对应的地震数目区间在120~130,最大频率为0.17。
|
图 5 汾渭地震带50年2万组模拟地震目录地震数目频率分布 |
数学期望、方差、标准差是随机变量的重要特性,反映了随机变量取值的平均水平、稳定程度、集中与离散的程度。对序列xi,则有
期望
| $ X = \frac{1}{N}\sum\nolimits_{i = 1}^N {{x_i}}, i = 1, 2, 3 \cdots, N $ | (8) |
方差
| $ {S^2} = \frac{1}{N}\sum\nolimits_{i = 1}^N {{{\left({{x_i} - X} \right)}^2}}, i = 1, 2, 3 \cdots, N $ | (9) |
对真值为
标准误差
| $ {\rm{MS}} = \sqrt {{S^2} + {{\left({X - \hat X} \right)}^2}} $ | (10) |
残差平方和
| $ {\rm{RRS}} = \sum\nolimits_i^k {{{\left({{y_k} - \hat y} \right)}^2}} $ | (11) |
其中,yk为实测值,
决定系数
| $ R = 1 - \frac{{{\rm{RRS}}}}{{{\rm{SST}}}} $ | (12) |
其中,SST为总平方和,
为检验生成的地震目录是否符合设定的地震活动性参数,以及是否满足地震活动泊松分布假设,分别统计每组目录每年4级以上地震发生次数,得到50个样本(T=50年),其中,发生地震i次(取值0,1,2,…)时,则地震年发生次数的概率密度ρ(i)为
| $ \rho \left(i \right) = \frac{i}{{50}} $ | (13) |
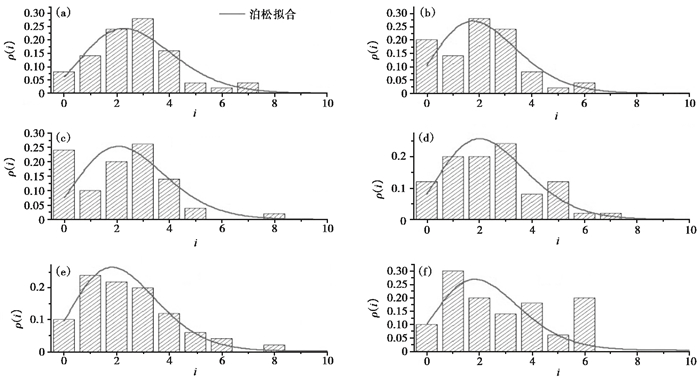
图 6给出了由6组随机选择的50年模拟地震目录用非线性拟合方法得到的4级以上年地震发生次数泊松分布拟合,表 2为每组拟合得到的地震年发生率v0及其误差参数。模拟地震年发生概率密度与拟合泊松概率密度值的拟合优度(决定性系数)均在大于0 8,残差平方和均在10-2数量级,由此可见,随机实验所生成的目录能较好符合泊松分布。
|
图 6 汾渭地震带6组50年模拟地震目录地震年发生次数泊松分布拟合 |
| 表 2 汾渭地震带6组50年模拟地震目录泊松分布检验与平均年发生率估计 |
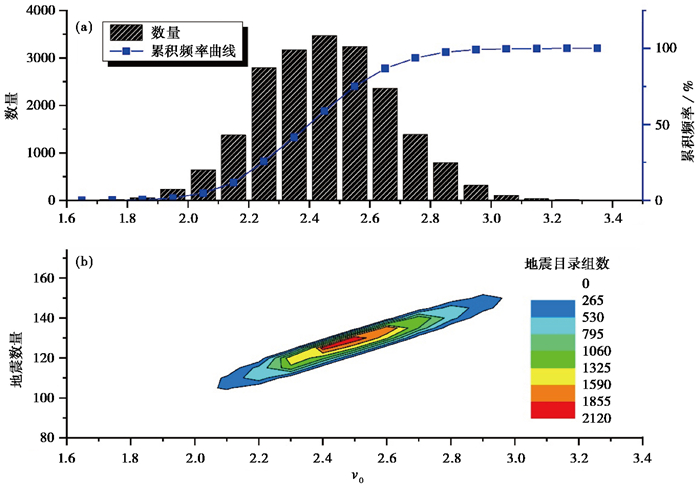
按上述方法计算2万组地震目录中每组目录的v0,其均值为2.46,标准差为0.22,以0.2为间隔,统计其分布(图 7)。由图 7(a)可见,峰值对应的v0为2.4~2.6,与设定值(2.5)基本接近。图 7(b)给出了2万组模拟地震目录,不同v0和不同地震数目对应的地震目录数量分布,当地震数目为120~130、v0为2.4~2.6时,地震目录组数最多,共2120组。
|
图 7 汾渭地震统计区样本地震数目与v0分布关系(T=50年) (a)v0峰值与数量间的关系;(b)不同地震数目与对应的地震目录数量分布 |
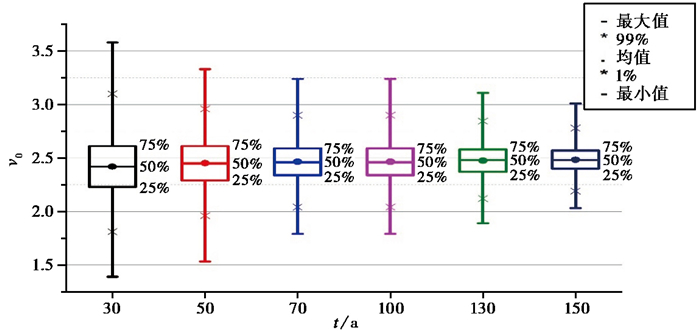
为了分析不同目录时长对于结果的影响,对30~150年不同时长各2万组的地震目录计算v0,并计算不同时长的均值、中位值、4分位区间、极值以及标准误差(图 8、表 3)。由图 8、表 3可见,目录时间越长,结果越收敛,均值越接近理论值,标准误差越小。
|
图 8 不同时长地震目录v0统计 方框内横线为中位值;方框表示4分位 |
| 表 3 模拟目录不同时长v0检验参数 |
表 4给出了模拟生成的2万组50年地震目录中,随机选择4组地震目录采用最小二乘法拟合计算得到的b值及参数。由表 4可见,拟合优度均大于0.9,残差平方和均小于0.4。
| 表 4 汾渭地震带4组50年模拟地震目录b值拟合检验参数 |
按相同方法计算2万组地震目录的b值,其均值为0.76,标准误差为0.13,以0.2为间隔,统计其分布(图 9)。由图 9(a)可见,峰值对应的b值为0.6,与设定值(0.78)接近。图 9(b)给出了2万组模拟地震目录在不同b值、地震数目时对应的地震目录数量分布。由图 9 (b)可见,当地震数目为120~130、b值为0.8左右时,地震目录组数最多,约540组。
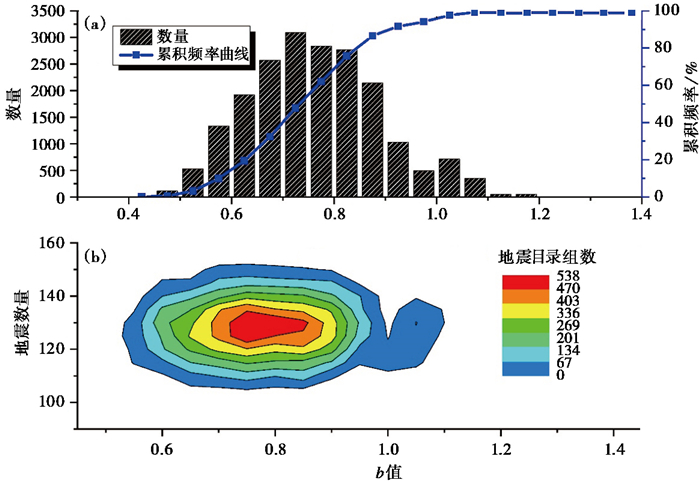
|
图 9 汾渭地震统计区年样本地震数目与b值分布间的关系(T=50年) (a)b峰值与数量;(b)不同地震数目与对应的地震目录数量分布 |
对30~150年不同时长各2万组的地震目录计算b值,求不同年限的均值、中位值、4分位区间、极值以及标准误差(图 10、表 5)。由图 10、表 5可见,目录时间越长,b值越收敛,标准误差和方差越小,越接近理论值。
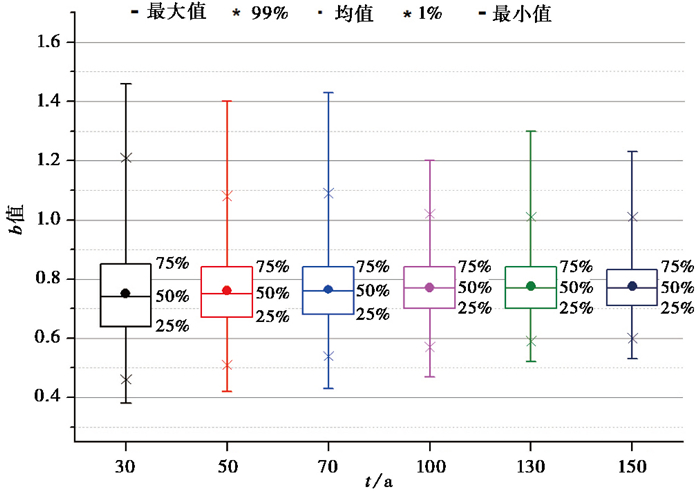
|
图 10 模拟目录不同时长b值统计 |
| 表 5 模拟目录不同时长b值检验参数表 |
模拟结果表明,无论是v0还是b值,模拟的地震目录时间越长,标准误差越小,均值越接近设定值,越能代表泊松模型描述的地震活动规律。
地震中长期预测是对某一地区今后数年到数十年地震形势和危险性的估计与预测(王晓青等,1996、2006),其结果既可直接服务于社会,又是短临预测的基础依据。本文采用上述模拟生成的2万组100年地震目录,统计指定震级的目录数占总目录的比例,得到汾渭地震带未来100年7级以上、8级以上地震的发震概率分别为0.66、0.19,与泊松模型理论计算的结果0.67、0.18基本一致。
汾渭地震带自1815年平陆6¾级地震以来,202年未发生6.5级以上地震,1998年张北6.2级地震以来,19年未发生6级以上地震。本文运用蒙特卡洛方法,模拟生成212年地震目录2万组,统计前202年没有发生6.5级地震的序列,并取最后10年,统计6.5级以上地震目录所占比例,得到汾渭地震带未来10年发生6.5级以上地震的条件概率为0.22;同理,得到汾渭地震带19年没有发生6.2级以上地震,未来10年发生6.2级以上地震的条件概率为0.31。
4 结论与讨论蒙特卡洛模拟通过对研究对象进行随机独立抽样,使其分布满足已知或设定概率分布来实现模拟。该方法通过大量重复实验,能够真实地接近实际物理过程,受几何条件限制小,对于小概率事件处理较好(Huh et al,2016)。通过改变地震事件的震级-频度关系形式、时间分布模型,采用蒙特卡洛模拟可得到各种复杂模型条件下的模拟地震目录。模拟目录在一定程度上填补了由于监测手段不足或历史记录不完整(无时间)、年代记载空缺所造成的地震目录缺失,使得那些长期无地震活动地区的地震序列更加完整。
基于地震活动的泊松分布模型、古登堡-里克特震级-频度(G-R)关系假设,运用反抽样法和直接抽样法生成随机数模拟地震目录,依据汾渭地震带的地震活动性参数,模拟了该地震带30、50、100年等不同时间长度的地震目录,检验结果表明,用该方法得到的地震目录体现了地震活动统计特征。在此基础上,应用模拟地震目录计算得到了汾谓地震带未来100年发生7级以上、8级以上地震的概率分别为0.66、0.19。以1815年平陆6¾级地震以来202年无6.5级以上地震和1998年张北6.2级地震以来19年无6级以上地震为条件,未来10年发生6.5级以上、6.2级以上地震的条件概率分别为0.22、0.31。
由于文中使用的时间上的泊松模型与真实地震活动常表现的丛集模型不一定吻合,考虑到地震之间的相互激发问题(泊松+丛集),今后可改变抽样函数,引入ETAS模型(Marzocchi et al,2009),以期在古地震记录较少地区以及地质结构复杂条件下能提供更精确的结果(Parsons,2008)。
致谢: 感谢中国地震局地球物理研究所提供的第5代地震动参数区划图资料。感谢陕西省地震局对地震目录资料收集给予的支持和帮助,感谢审稿专家的意见和建议。| 毕金孟, 蒋长胜. 2017, 可操作的地震预测(OEF)国际研究动态综述. 中国地震, 33(1): 1–13. |
| ConsoleR, CarluccioR, PapadimitriouE, 等. 2016, 用合成地震目录模拟希腊科林斯湾断层系的地震活动. 李红译, 世界地震译丛, 47(4): 309–328. |
| 傅征祥, 姜立新, 王晓青. 1995, 地震损失概率预测研究中的地震危险性分析方法探讨. 中国地震, 11(1): 49–53. |
| 高孟潭. 2015, GB 18306-2015《中国地震动参数区划图》宣贯教材. 北京: 中国质检出版社. |
| 郭星. 2015, 强震复发的随机特征滑动模型及其应用方法研究. 国际地震动态(2): 45–47. |
| 郭星, 潘华. 2016, 一种基于蒙特卡罗模拟的发震概率计算方法. 地震学报, 38(5): 785–793. DOI:10.11939/jass.2016.05.012 |
| 胡聿贤. 2006, 地震工程学(第2版). 北京: 地震出版社. |
| 蒋长胜, 吴忠良, 庄建仓. 2013, 地震的"序列归属"问题与ETAS模型——以唐山序列为例. 地球物理学报, 56(9): 2971–2981. DOI:10.6038/cjg20130911 |
| 金欣, 周仕勇, 杨婷. 2017, 地震活动性模拟方法及太原地区地震活动性模拟. 地球物理学报, 60(4): 1433–1445. DOI:10.6038/cjg20170417 |
| 李红, 邓志辉, 邢成起, 等. 2015, 人工地震目录研究进展. 地球物理学进展, 30(5): 1996–2006. |
| 廖景高, 赵其华, 刘宇, 等. 2014, 基于Monte-Carlo的滑坡失稳概率计算研究. 长江科学院院报, 31(7): 29–33. |
| 刘桂萍, 傅征祥, 刘杰. 2000, 摩擦时间依从的地震活动性细胞自动机模型. 地球物理学报, 43(2): 203–212. |
| 刘桂萍, 石耀霖, 马丽. 1995, 地震活动性的细胞自动机模型. 西北地震学报, 17(2): 20–25. |
| 刘甲美, 高孟潭, 吴树仁. 2016, 概率性地震滑坡危险性区划方法及其应用. 岩石力学与工程学报, 35(增刊Ⅰ): 3100–3110. |
| 刘善琪, 李永兵, 田会全, 等. 2013, 影响b值计算误差的Monte Carlo实验研究. 地震, 33(4): 135–144. |
| 潘华, 高孟潭, 谢富仁. 2013, 新版地震区划图地震活动性模型与参数确定. 震灾防御技术, 8(1): 11–23. DOI:10.11899/zzfy20130102 |
| 石耀霖, 刘杰, Vere-JonesD, 等. 1998, 力学和统计模型结合研究人工合成地震活动性及其对预报真实地震的启示. 地震学报, 20(4): 363–372. |
| 陕西省地震局. 2005, 陕西省地震目录. 公元前1189年至公元2001年, 北京: 地震出版社. |
| Sólnes J、Halldórsson B, 1997, 合成地震目录的生成: 应用于地震灾害及危险性的评估, 孙清杰译, 世界地震译丛, (4), 55~60. |
| 唐春安. 1997, 岩石声发射规律数值模拟初探. 岩石力学与工程学报, 16(4): 268–274. |
| 唐春安, 傅宇方, 赵文. 1997, 震源孕育模式的数值模拟研究. 地震学报, 19(4): 337–346. |
| 王继, 徐扬, 张丽, 等. 2002, 汾渭地震带的b值和年平均发生率的研究. 山西地震(3): 22–24. |
| 汪素云. 1999, 中国近代地震目录:公元1912年-1990年MS ≥ 4.7. 北京: 中国科学技术出版社. |
| 王晓青, 傅正祥. 1996, 2005年前中国大陆地震震级概率预测. 地震学报, 18(4): 420–426. |
| 王晓青, 张国民, 傅征祥, 等. 2006, "2006-2020年中国地震危险区与地震灾害损失预测研究"项目成果介绍. 国际地震动态(9): 88–93. |
| 徐伟进, 吴健. 2017, 余震时空丛集对概率地震危险性分析的影响. 地球物理学报, 60(8): 3110–3118. DOI:10.6038/cjg20170818 |
| 赵宏, 屈娥. 2015, 地震活动统计与理论地震目录的设计实验. 管理工程师, 20(3): 73–76. |
| 周仕勇. 2008, 川西及邻近地区地震活动性模拟和断层间相互作用研究. 地球物理学报, 51(1): 165–174. |
| 朱元清, 石耀霖. 1991, 地震活动性研究中的非线性动力学模型. 地球物理学报, 34(1): 20–31. |
| Assatourians K, Atkinson G M. 2013, EqHaz:An open-source probabilistic seismic-hazard code based on the Monte Carlo simulation approach. Seismol Res Lett, 84(3): 516–524. DOI:10.1785/0220120102. |
| Bourne S J, Oates S J, Bommer J J, et al. 2015, A Monte Carlo method for probabilistic hazard assessment of induced seismicity due to conventional natural gas production. Bull Seismol Soc Am, 105(3): 1721–1738. DOI:10.1785/0120140302. |
| Burridge R, Knopoff L. 1967, Model and theoretical seismicity. Bull Seismol Soc Am, 57(3): 341–371. |
| Cornell C A. 1968, Engineering seismic risk analysis. Bull Seismol Soc Am, 58(5): 1583–1606. |
| Ebel J E, Kafka A L. 1999, A Monte Carlo approach to seismic hazard analysis. Bull Seismol Soc Am, 89(4): 854–866. |
| Hagiwara Y. 1974, Probability of earthquake occurrence as obtained from a Weibull distribution analysis of crustal strain. Tectonophysics, 23(3): 313–318. DOI:10.1016/0040-1951(74)90030-4. |
| Hainzl S, Marsan D. 2007, Dependence of the Omori-Utsu law parameters on mainshock magnitude:observations and modeling. In:AGU Fall Meeting Abstracts, San Francisco, CA, USA:AGU. |
| Huh U, Cho W, Joy D C. 2016, Monte Carlo modeling of ion beam induced secondary electrons. Ultramicroscopy, 168: 28–33. DOI:10.1016/j.ultramic.2016.05.010. |
| Iervolino I, Chioccarelli E, Cito P, 2016, REASSESS V1. 0: A computationally-efficient software for probabilistic seismic hazard analysis, In: ECCOMAS Congress 2016, Ⅶ European Congress on Computational Methods in Applied Sciences and Engineering, Crete Island, Greece: ECCOMAS. |
| Marzocchi W, Lombardi A M. 2009, Real-time forecasting following a damaging earthquake. Geophys Res Lett, 36(21): L21302. DOI:10.1029/2009GL040233. |
| Mogi K. 1962, Study of elastic shocks caused by the fracture of heterogeneous materials and its relations to earthquake phenomena. Bull Earth Res Inst, 40: 125–173. |
| Mohammed T, Atkinson G M, Assatourians K. 2014, Uncertainty in recurrence rates of large magnitude events due to short historic catalogs. J Seismol, 18(3): 565–573. DOI:10.1007/s10950-014-9428-1. |
| Musson R M W. 2000, The use of Monte Carlo simulations for seismic hazard assessment in the UK. Ann Geophys, 43(1): 1–9. |
| Nishenko S, Buland R. 1987, A generic recurrence interval distribution for earthquake forecasting. Bull Seismol Soc Am, 77(4): 1382–1399. |
| Parsons T. 2008, Monte Carlo method for determining earthquake recurrence parameters from short paleoseismic catalogs:Example calculations for California. J Geophys Res, 113(B3): B03302. |
| Pavel F, Vacareanu R. 2017, Evaluation of the seismic hazard for 20 cities in Romania using Monte Carlo based simulations. Earthq Eng Eng Vib, 16(3): 513–523. DOI:10.1007/s11803-017-0400-2. |
| Rhoades D A, Robinson R, Gerstenberger M C. 2011, Long-range predictability in physics-based synthetic earthquake catalogues. Geophys J Int, 185(2): 1037–1048. DOI:10.1111/gji.2011.185.issue-2. |
| Setiawan B. 2017, Probabilistic Seismic hazard analysis incorporating Monte Carlo method in the case of Adelaide region. Indones J Geosci, 4(2): 81–96. |
| Shaw D, Yeh C H, Jean W Y, et al. 2007, A probabilistic seismic risk analysis of building losses in Taipei:An application of Haz-Taiwan with its pre-processor and post-processor. J Chin Inst Eng, 30(2): 289–297. DOI:10.1080/02533839.2007.9671255. |
| Wang J P, Wu Y W. 2014, A new seismic hazard analysis using FOSM algorithms. Soil Dyn Earthq Eng, 67: 251–256. DOI:10.1016/j.soildyn.2014.10.006. |
| Weatherill G. 2009, A Monte Carlo approach to probabilistic seismic hazard analysis in the Aegean region.Ph.D thesis. Norwich: University of East Anglia |
| Working Group on California Earthquake Probabilities. 2003, Earthquake probabilities in the San Francisco Bay Region.2002-2031. Open-File Report. |
| Yazdani A, Shahpari A, Salimi M R. 2012, The Use of Monte-Carlo simulations in seismic hazard analysis in Tehran and surrounding areas. Int J Eng, 25(2): 159–165. |
| Youngs R R, Coppersmith K J. 1985, Implications of fault slip rates and earthquake recurrence models to probabilistic seismic hazard estimates. Bull Seismol Soc Am, 75(4): 939–964. |
| Zhou S Y, Johnston S, Robinson R, et al. 2016, Tests of the precursory accelerating moment release model using a synthetic seismicity model for Wellington. New Zealand, J Geophys Res, 111(B5): B05308. DOI:10.1029/2005JB003720. |
 2018, Vol. 34
2018, Vol. 34



