2个地震台站记录的背景噪声的互相关函数(Noise Cross-Correlation Function,NCF),可以近似地表征这2个台站之间的格林函数(Wapenaar,2004)。自Shapiro等(2005)利用美国加州地区地震台站间NCF中的面波信号对该地区进行高精度的成像研究以来,基于背景噪声互相关技术的地震学研究飞速发展,已被广泛地应用于对地下介质的结构探测和状态变化的监测中(Brenguier et al,2008;Yao et al,2008;刘志坤等,2010;Zheng et al,2011)。有关噪声地震学的发展历史和进展可参见Campillo等(2015)以及徐义贤等(2015)的综述文章。地震观测一直是推动地震学发展的重要因素,目前,越来越多的大型地震观测台阵被广泛布设,其中,具有代表性的如美国的USArray以及中国的中国地震科学台阵探测计划(China Array)。这些观测台阵往往由几百到上千个观测台站组成,观测时长从几个月到几年。密集的地震观测台阵结合噪声互相关计算,可以使得我们更好地对地下介质进行采样,获取更高精度的地下结构的图像(Lin et al,2011;Bao et al,2015)。与之对应的则是,获取密集台站间NCF所需的计算量以正比于台站数目平方的方式增长,这使得计算时间大大增加。
噪声互相关方法的主要特点是,通过互相关计算可以获取在2个地震台之间传播的地震波。理论上,对于N个台站,我们可以获得N*(N-1)/2个台站对间的NCF,这可以大大提高探测地下介质所需路径的覆盖密度。同时,为了获取高信噪比、稳定的NCF信号,一般需要对长时间的连续记录的互相关函数进行叠加(Bensen et al,2007)。换言之,如果连续记录的时长为T,记录台站数为N,则获取NCF所需要的总的计算量将正比于N2和T。因此,对密集台站间的NCF所需的计算量以正比于台站数目平方的方式增长,这使得计算时间大大增加。早期的背景噪声互相关主要利用地震记录中垂直分量数据计算垂向分量间的互相关。近期,利用地震台站的三分量连续记录获取九分量NCF的方法得到了广泛应用,并显示了一定的优势。首先,通过改进NCF的计算方法,可以保留九分量NCF中瑞利面波在径向(R)和垂向(Z)的瑞利面波的振幅比,研究人员称之为HV比(Lin et al,2014)或ZH比(Chong et al,2015;Li et al,2016)。该振幅比反映的是瑞利面波的偏振椭圆率的特征,可用来反演地下介质的横波速度结构(Yano et al,2009)。ZH比可以反映更浅部的信息,有助于对浅部地壳横波速度的精细成像研究(Lin et al,2014;Li et al,2016)。其次,利用九分量的NCF,我们可以获取在台站间传播的勒夫面波,从而对介质波速进行独立的测量(Tomar et al,2017)。最后,利用九分量NCF中瑞利面波的波形和偏振特征,我们可以利用NCF对地震计的水平方位角度进行准确性评估和校正(Zha et al,2013),而这对于获取可靠的各向异性结果十分重要。综合来看,相比垂直分量间NCF,九分量NCF可以提供更多的信息,值得深入探索。然而,仅就分量数目而言,同样的台站数目下获取九分量NCF的计算量为仅计算垂直分量间NCF的9倍,计算量有近乎1个数量级的增长。由后文可知,在传统的高性能计算服务器上,获取海量台站之间九分量NCF所需时间需要几个月乃至1年。这使得我们需要寻求新的计算技术,以期在合理的时间内完成NCF的计算。
随着地震观测技术的发展,地震学研究也进入了大数据时代。地震学家已经开始探索将信息学科里的数据挖掘、机器学习及云计算等方法应用于地震学研究中(Yoon et al,2015;Riahi et al,2016;Magana-Zook et al,2016)。云计算是在网格计算和分布式计算技术上发展起来的现代计算技术,可以通过互联网为用户提供计算能力和存储服务。云计算将计算任务分布在大量计算机构成的资源池上,以使得各种应用可根据需要获取计算能力和存储空间等服务(Wang et al,2010)。为解决大数据时代数据量的增加给计算能力带来的压力,研究人员已经成功地将云计算应用于处理地震和InSAR数据等数据密集型任务(Heilmann et al,2013;Zinno et al,2015)。密集台站记录的海量数据间NCF的计算,是一种典型的数据密集型计算,故可以使用云计算方法实现加速。
2013年8月~2016年5月,中国地震局地球物理研究所等单位在青藏高原东北缘南北地震带北段开展了China Array二期的地震学台阵观测研究。观测期间共布设了674套宽频带流动地震仪,观测时长超过2年。为利用九分量NCF对该地区的波速结构进行研究,本文提出了一种基于云计算的计算方法,该方法可快速地完成密集台站间九分量NCF的计算。我们将其应用于China Array的数据,计算获得了稳定可靠的九分量NCF波形。同时,我们通过对所得NCF数据及天然地震中瑞利面波ZH比的分析,验证了计算方法和云计算系统的可靠性。
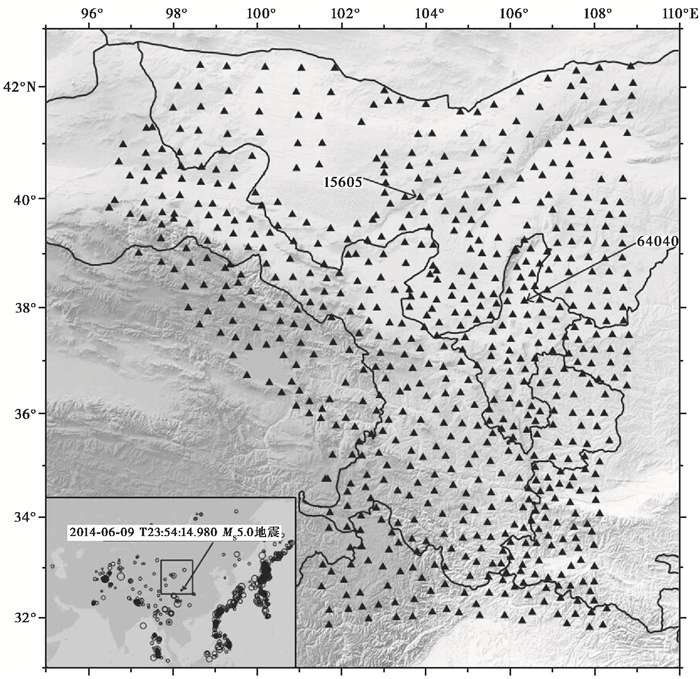
1 数据及九分量NCF的计算方法、计算规模图 1为在青藏高原东北缘布设的674个宽频带地震台站的分布。这些台站均为宽频带,较为均匀地分布在1000km×1000km的观测区域内,平均台间距约为50km。台站的观测仪器有REFTEK-130B+Guralp 3ESPC-60和REFTEK130S+Guralp 3T-120S两种组合,原始采样率均为100Hz。大部分台站的观测时间均超过2年,原始数据总量超过15TB。利用这些密集台站的观测数据,可以计算台站间的NCF,旨在为青藏高原东北缘的成像研究提供密集的NCF路径覆盖。同时,长时间的连续观测数据,也为获取高信噪比的NCF波形提供了保障。
|
图 1 南北地震带北段China Array二期密集台站及周边地震震中分布 黑色三角为宽频带地震台站,其中以箭头标出的X2.15605和X2.64040台被后文用于测量NCF及地震事件中瑞利面波的ZH比;左下角图中方框表示了密集台站的粗略位置,圆圈为2014~2015年距台阵中心3000km内发生的5~6级地震,用箭头标出的地震被用以分析地震产生的瑞利面波在上述2个台站的偏振特征 |
九分量NCF的计算流程与Bensen等(2007)描述的计算垂直分量间NCF的流程类似,只是在进行数据的时域、频域归一化时略有不同,简述如下。主要计算流程如图 2所示。

|
图 2 九分量NCF计算流程 步骤①、②分别显示了原始数据的预处理及频谱转换流程;步骤③显示了九分量NCF计算、叠加和旋转 |
首先,将原始数据抽样至1Hz,之后去除仪器响应,去均值,去线性分量,对于每一个地震台的每一个分量,以天为单位保存文件,最后,对每一个地震台每天的三分量记录,对其进行时域平均和频谱白化处理。在进行时域平均时,使用Bensen等(2007)提出的滑动窗平均方法,窗长为120s。为了保持九分量NCF中信号的相对振幅比与Lin等(2014)的类似,首先计算三分量数据绝对值的平均值,将三分量数据均除以该平均值来实现时域的均一化处理。同样,在后续频谱白化中,也先求取三分量数据的频谱平均值,用该平均值对三分量的频谱数据进行反向加权以实现频域白化处理。虽然这些非线性处理会改变最终NCF波形的绝对数值,但利用三分量平均值来进行时域和频域的预处理可以保持不同分量间波形的相对振幅比(Lin et al,2014;Li et al,2016)。然后,将每一个台站每个分量经过频域白化后的频谱数据存储为1个文件,用以表征其三分量的频谱数据。在完成上述步骤后,对于任意2个台站三分量的单天数据,利用其频谱进行互相关计算,以得到单天的NCF。为了获取九分量的NCF,对于2个台站构成的台站路径,分别有ZE、ZN、ZZ等共计9个分量的组合。考虑存储空间和研究需要的平衡,对于每个分量的NCF,保留了延时在-3600~3600s的数据。在获取了1个路径上多天的九分量NCF之后,对于每个分量组合,将这些天的NCF分别进行叠加,获取叠加之后的ENZ性质的叠加NCF。为了获得最终径向(R)、切向(T)和垂向(Z)形式的NCF,需要将ENZ形式的NCF进行旋转,以获得RTZ形式的NCF。对于2个台站A和B所形成的路径AB,将A视为地震,B视为记录台站,计算矢量

|
图 3 计算流程 |
由图 3可知,台站间九分量NCF的总体计算量主要由台站间形成路径的数目以及参与计算的天数来共同决定。当台站数目较大、记录时间较长时,完成其NCF计算所需要的存储空间和对计算能力的要求都较高。以计算674个台站2014~2015年2年间1Hz采样率的九分量NCF为例,两两台站间可以形成226801条台站路径,作为输入文件的单天三分量数据达到1476060条,所需存储空间为1.2TB。如以计算时长为730天,单个分量的NCF时长7200s来计算,则完成所有九分量NCF的计算,需要计算单天单分量组合的NCF达14.9亿条,占用空间约44TB。我们在1台高性能的服务器上(XEON E5-2620*2,64GB内存,80TB RAID5磁盘阵列)上测试了完成10万条路径30天单分量NCF的计算和叠加的计算时长,发现其耗时接近8h。由于总体计算量正比于需要计算的单天NCF数据,由此推算,完成整个数据集合的NCF计算时间需要3840h,接近6个月。
由此可见,海量数据集合间NCF的计算对存储空间和计算能力都有很高的需求,无法在传统的高性能计算机上快速完成。因此,我们设计了一套基于云计算的计算系统,以完成海量NCF数据的加速计算。
2 密集台站间九分量NCF计算的云平台实现密集台站间NCF的计算是一种数据密集型的计算,其总体计算量的庞大主要源于参与计算的数据量的庞大。其对于传统计算模式的挑战主要有2点,首先,参与计算的输入、输出数据的存储空间十分巨大,再者,总体计算量的庞大导致计算不能在短期内完成。针对这2个问题,我们使用了阿里云公司提供的云计算服务来解决其存储和计算瓶颈。具体而言,我们使用了阿里云提供的对象存储服务(Objective Storage Service,OSS)和批量计算服务(Batch Computing Service,BCS)云服务。OSS存储服务可以提供文件的持久化存储,实现文件的快速读取和写入,并且具有近乎无限的存储拓展空间,因此,可用来存储NCF计算中的输入、输出文件。而BCS批量计算服务则可提供可控的、弹性的计算能力,根据用户的需求,BCS可以提供几百乃至上千个虚拟的计算服务器用于完成用户指定的计算。
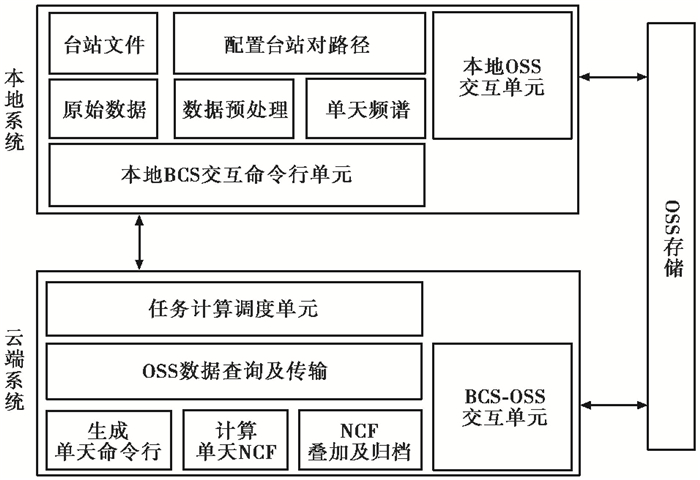
阿里云的OSS、BCS提供了基于云平台的通用的存储和计算服务,基于这些服务,我们设计了一套NCF计算系统以实现密集台站间NCF的快速计算。整个计算系统由本地系统和云端系统2部分组成,分别完成不同的数据处理任务,其总体架构如图 4所示。
|
图 4 基于阿里云计算服务的密集台站NCF计算系统架构 计算系统由本地系统和云端系统组成,二者以OSS为媒介进行数据交换 |
本地系统主要负责数据的预处理以及系统的配置任务,我们按照图 2中的前2个步骤完成数据的预处理,生成所需的单天频谱文件。之后,将对应的频谱文件上传至OSS作为云端系统的输入文件之一。同时,根据给定的台站信息,本地系统将生成需要参与NCF计算的台站对路径信息,并对需要参与计算的天数予以控制。
云端系统主要负责计算密集型任务,即图 2中步骤③的计算任务。在频谱文件传入OSS之后,基于BCS的云端系统可以读取这些频谱文件作为计算NCF的输入文件。海量NCF计算的加速效果主要是利用BCS提供的弹性的计算能力来实现。由于BCS可以根据用户指定启动多个虚拟服务器同时运行,每一个服务器只完成整体计算量中的一部分,因此,通过同时启动多个虚拟服务器,可大大减少完成整体计算所需的时间。
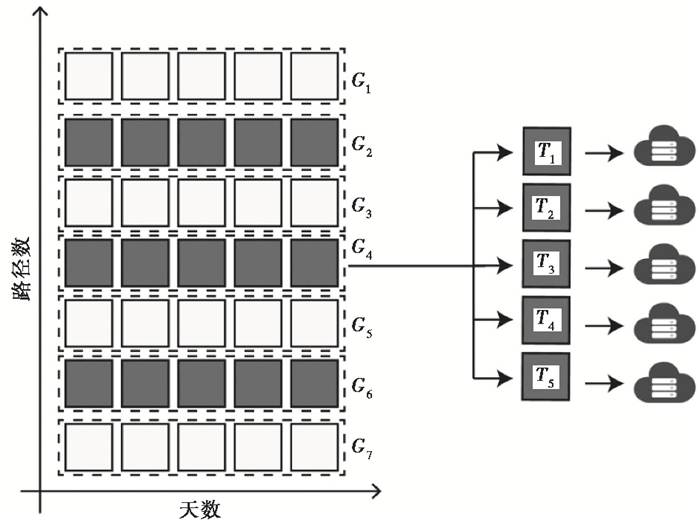
实现NCF计算在云端系统的加速,关键问题在于如何实现对整体计算量进行合理的、自动的分配,以实现化整为零,同时运行。我们在云端系统实现了NCF的计算和叠加,并设计了计算模块来完成计算任务的划分与调配,任务划分思路如图 5所示。由上述讨论可知,NCF的总体计算量主要由参与计算的路径的数目N和参与计算的天数T所决定,因此,我们采取了两步划分的策略。首先,将N条路径分成n份,每一份当中含有的路径数目为N/n条,形成n个路径群组,即G1至Gn。同时,将总的计算天数T分割为m份,每一份当中需要计算的天数为T/m,从而形成m个时间切片,即T1至Tm。对于每一个路径群组Gn,我们均向云端系统发送请求,请求启动m个虚拟服务器来完成该路径群组在所有参与计算的天数T上的NCF计算。每一个启动的虚拟服务器都有1个唯一的编号K,对于第K个虚拟服务器,它只负责计算路径群组Gn在时间切片TK时间段内NCF的计算和叠加。当任意一个虚拟服务器启动运行后,都会查询与其负责的计算任务相关的输入数据,将其由OSS传输至该虚拟服务器的磁盘,之后进行在时间切片TK内单天NCF的计算及在TK时段内的叠加。在完成相应计算任务后,虚拟服务器将输出数据压缩归档,回传至OSS供用户下载进行后续分析,完成之后释放所有计算资源。利用上述的任务分割和调度策略,可将整体计算量平均分配到mXn个虚拟服务器中同时运行,从而实现了整体计算任务的颗粒化划分,最终完成加速任务。
|
图 5 利用云计算方法实现总量计算的分解策略示意图 |
我们利用上述方法计算了南北地震带北段674个地震台2014~2015两年内所有台站间的九分量NCF。首先,将674个台站间形成的226801个台站路径拆分为20个路径群组,并将2年的时长拆分为24个时间切片,每个切片约30天。然后,对于每一个路径群组,在云端系统上请求24个虚拟服务器来进行该群组对应NCF的计算。为了完成整个数据集的NCF计算,我们在云端系统上共启动了480个虚拟服务器,每一个服务器负责约11000条路径30天的九分量NCF计算和叠加。在计算中,没有保存单天的NCF波形,而仅将月尺度叠加后的九分量NCF传输到OSS进行存储,这对于研究该地区的地下结构信息影响不大,但却可以大幅减少不必要的数据传输。同时,由于研究的需要,也没有对叠加后的NCF进行旋转,而是保留了其原始的ENZ形式。
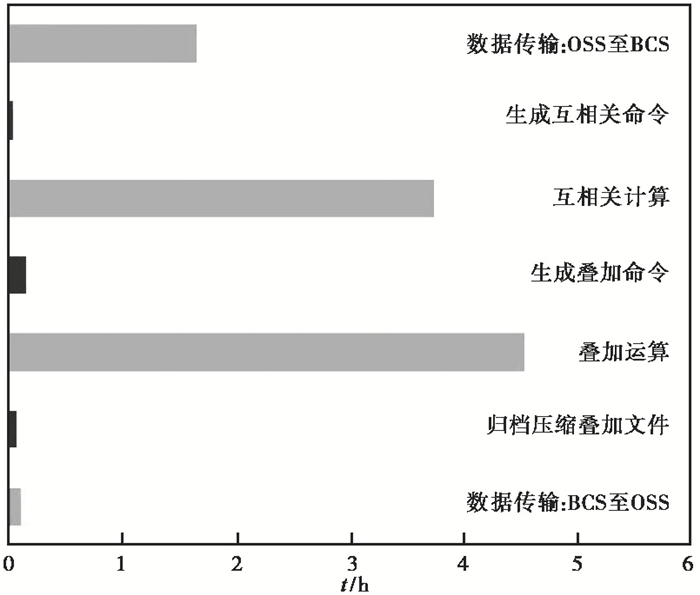
由于BCS上启动的多个虚拟服务器可同时运行,因此,完成总体计算的时间主要取决于在单台虚拟服务器上完成其负责的计算任务所需的时间。我们对在云端系统计算NCF所需的主要计算步骤的耗时进行了记录,并计算了这些计算步骤在480个虚拟服务器上运行耗时的平均值(图 6)。由图 6可见,数据在单天NCF的计算和叠加以及数据在OSS与BCS间的数据传输是主要的耗时部分。但综合来看,每个虚拟服务器完成计算的时间平均约为10.2h,相比在传统高性能服务器上6个月的耗时有近400倍的加速效能。
|
图 6 云端系统各个主要计算步骤的耗时平均 |
利用BCS完成总计算的加速,核心在于BCS系统可提供多台虚拟服务器同时运行。如果不考虑BCS与OSS数据传输的时间消耗,理论上完成总体计算的时间与同时调用的虚拟服务器的数量成反比。由于部分研究需要以月尺度叠加的NCF数据作为输出,因此,本文中将整体2年的时长划分为24个时间切片。理论上,我们可以通过增加路径群组数m和时间切片数n实现更多虚拟服务器的同时调用,以进一步减少计算时间。
3 九分量NCF中瑞利面波ZH比的测量及验证相比垂直分量间的NCF,九分量NCF的一个重要优势是可通过测量瑞利面波垂向振幅与径向振幅的ZH比来对地壳浅部横波速度进行研究(Lin et al,2014;Li et al,2016)。同时,分析九分量中瑞利面波ZH比的分布特征,也是对上述九分量NCF计算可靠性的一种检验方式。因此,我们对利用云计算模式得到的九分量NCF中瑞利面波的ZH比进行了测量,并与从天然地震面波中得到的同周期ZH比进行了交叉比对。
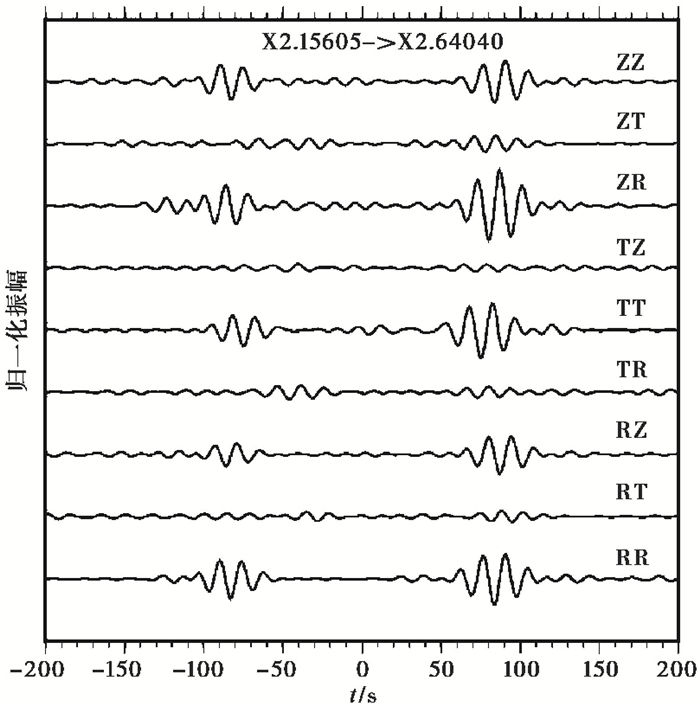
首先,将OSS上存储的按月叠加的ENZ形式九分量NCF下载至本地,并对其进行进一步的叠加处理,获得了2014~2015年2年叠加的ENZ形式的九分量NCF,再将其按照旋转矩阵公式进行旋转,转化为RTZ形式。图 7显示了台站对路径X2.15605至X2.64040对应的RTZ形式的九分量NCF波形。对于每一个NCF,其时间轴正值表示从台站X2.15605传播至X2.64040的信号,负值则表示由X2.64040传播至X2.15605的信号。由图 7可见,在ZZ、ZR、RZ、RR分量上均可以看到明显的瑞利面波信号,在TT分量上则可以观察到勒夫面波信号。在相互正交的ZT、TZ、RT、TZ分量上,在相应时间窗口内几乎没有强信号出现。在正交分量面波时间窗口内存在的微弱信号,很可能是局部散射效应导致的偏离大圆路径的散射波干涉而成。图 7中各个分量之前波形的到时和相对振幅特征,显示了我们计算得到的九分量NCF的可靠性。为进一步对其进行验证,我们对NCF中瑞利面波的偏振特征和ZH比进行了测量分析。
|
图 7 台站对X2.15605至X2.64040路径上2014~2015两年叠加的九分量波形 NCF波形经过了12~20s周期的带通滤波;振幅按照九分量中振幅最大值进行了归一化处理 |
在九分量NCF中,瑞利面波主要分布在Z、R分量的组合上。对于2个台站A和B形成的路径AB,我们认为A是激发点,B为接收点,并使得NCF中时间轴正值的信号表征从A传往B的信号。在此假定下,九分量NCF中正半轴的ZZ、ZR分量表征的是接收点的Z、R分量上对激发点Z分向作用力的响应,而RZ、RR分量则表征接收点的Z、R分量上对激发点R分向作用力的响应(Li et al,2016)。由于瑞利面波的偏振特征和ZH比主要反映接收台站下方的波速结构特征,因此,我们往往使用AB路径上正半轴的波形来进行测量,以表征B台站下方波速的特征。而对于A台站,则可以根据互异性将AB路径进行时间翻转来测量。
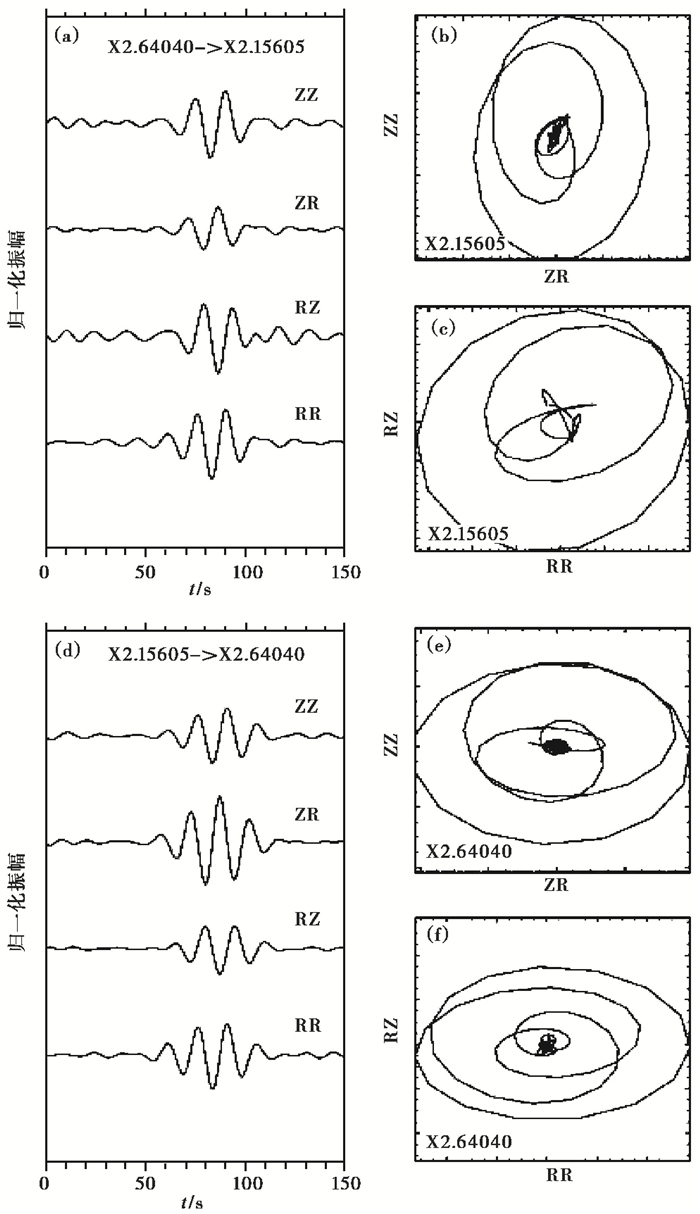
图 8(a)为由X2.64040传播至X2.15065的Z、R分量4种组合的瑞利面波波形。所有波形都进行了中心周期为16s的窄带滤波,并对振幅进行了统一的归一化处理以显示其相对大小。图 8(b)、8(c)分别为ZZ与ZR的分量组合以及RZ与RR分量组合上瑞利面波的偏振信息。由于只使用了正半轴的信号,因此,其反应的是台站X2.15605下方的速度特征。同时,我们也计算了由X2.15605传播至X2.64040的对应分量组合的NCF波形,并进行了相同的处理(图 8(d)、8(e)、8(f))。由图 8可见,无论是在ZZ与ZR的组合上,还是在RZ与RR的组合上,面波信号的偏振方向都表现出了逆进椭圆的特征,符合瑞利面波的偏振属性。这表明,九分量NCF波形保持了水平分量的相对振幅比例,进而保持了其偏振特征。由图 8还可见,在X2.64040、X2.15605台站中瑞利面波垂向与径向的振幅ZH比有明显差异。就16s周期的面波而言,X2.15605的ZH比大于1,而X2.64040的ZH比小于1。
|
图 8 X2.15605、X2.64040路径上不同Z与R分量组合的16s瑞利面波波形及偏振图像 (a)由X2.64040传播至X2.15065的Z、R分量4种组合的瑞利面波波形;(b)、(c)X2.15605台ZZ与ZR的分量组合以及RZ与RR分量组合上瑞利面波的偏振信息;(d)由X2.15605传播至X2.64040的Z、R分量4种组合的瑞利面波波形;(e)、(f)X2.64040台ZZ与ZR的分量组合以及RZ与RR分量组合上瑞利面波的偏振信息 |
在NCF的计算中,噪声源的特征以及记录信号本身的质量会对提取到的信号有一定的影响。如图 8(b)、8(c)中的偏振图像虽然都符合瑞利面波的偏振,但其具体形态仍有一些差异。为了获取稳定的测量值,我们往往需要对多条路径上瑞利面波的ZH比进行统计平均,以更好地表征某一台站在特定周期的可靠ZH比测量值。研究区域内密集分布的台站为我们提供了优良的路径分布,因此,分别以X2.15605、X2.64040为中心,选取周边台站传播至中心台站的瑞利面波信号,对其16s周期的瑞利面波ZH比进行测量。为了实现九分量NCF中瑞利面波ZH比的快速测量,依据如下标准对这些台站路径进行了筛选处理:
(1) 对于中心台站,只选取台站间距大于3倍的对应周期的面波波长来进行测量。这样可以满足在噪声互相关中的远场假设,以减小系统性偏差。
(2) 在传播至中心台站的4个分量ZZ、ZR、RZ、RR上,对应瑞利面波的信噪比要大于8。
(3) 对ZR或RR方向上的波形进行希尔伯特变换后,对应周期的瑞利面波与ZZ或RZ波形的相关系数需大于0.8。
对于符合上述准则的任意一个路径上的NCF,我们将ZR进行希尔伯特变换后,求取其包络在对应周期面波到时的最大值。之后,求取ZZ分量包络的最大值,并以ZZ、ZR两个包络的最大值之比作为该台站对应周期瑞利面波的1个ZH比测量值。同时,对RR、RZ分量进行相同的处理,以获取另外1个ZH比的测量值。如果4个分量的2组组合均满足上述筛选标准,则对于每一个路径,都可以获得2个有效的ZH比值。
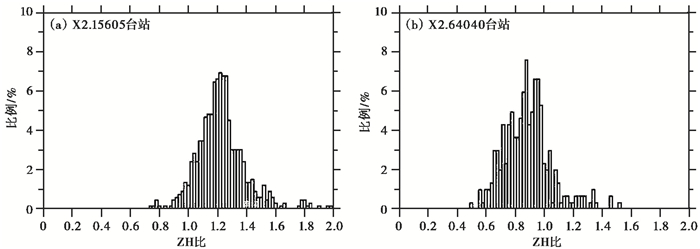
我们分别以X2.15605、X2.64040台站为中心,对周期16s的瑞利面波ZH比进行了上述测量,其ZH比的分布如图 9所示。其中,X2.15605台站共有676次有效测量,其ZH比的平均值为1.213。X2.64040台站共有304次有效测量,其ZH比的平均值为0.875。其有效测量数目的不同与每个中心台站周边的台站分布相关,也与不同方向、距离上NCF中信号的差异有关。由图 9可见,2个台站的ZH比分布均呈现高斯钟型,其标准方差分别为0.161、0.152。
|
图 9 九分量NCF中16s瑞利面波的ZH比分布 |
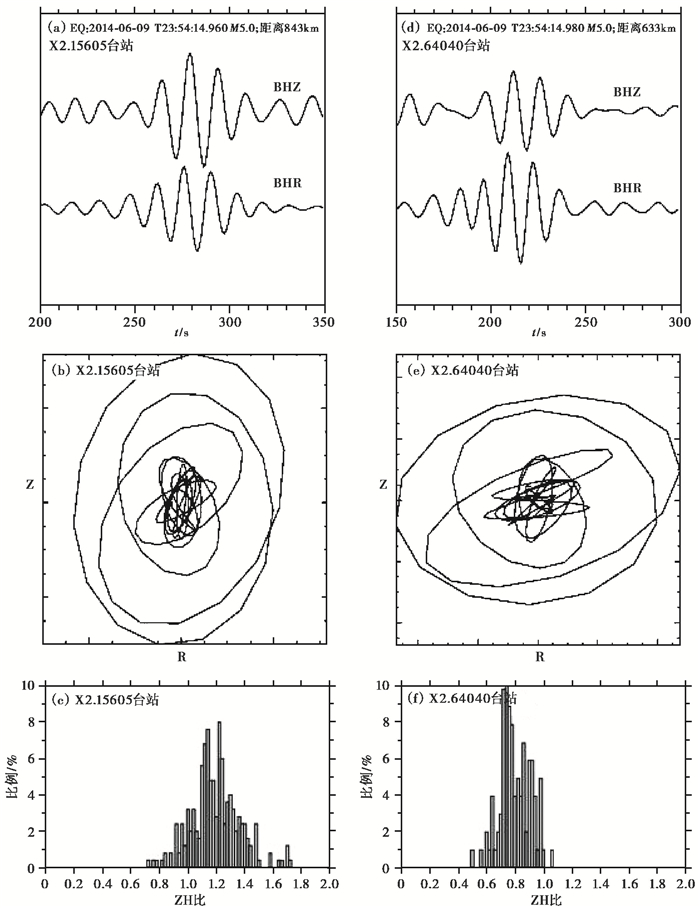
为了进一步对测量得到的ZH比进行确认,我们也利用这2个台站记录到的天然地震中的瑞利面波对其ZH比进行了测量。选取2014年6月9日发生的1次5级地震,对该地震产生的16s周期的瑞利面波在2个台站上的偏振特征进行了分析(图 9),地震的位置、发震时间如图 1中内图所示。对于2个台站,首先将记录的三分量波形旋转到R、Z方向,进而进行16s的窄带滤波。由图 9可见,该地震在2个台站上瑞利面波的ZH比特征与九分量NCF中显示的同周期面波ZH比的特征类似,即在X2.15605台站上较大,X2.64040台站上较小。我们进而对2个台站共同记录到的2014~2015年发生的5~6级地震的瑞利面波进行了ZH比的测量和统计平均。共选取632个距台阵中心小于3000km的天然地震,其分布如图 1中内图所示。在测量天然地震16s的瑞利面波的ZH比时,我们采用了前述的信噪比和互相关系数准则。测量结果如图 10(c)、10(f)所示。其中,图 10(c)显示了X2.15605台站获取的251次有效测量,其ZH比平均值为1.198,标准方差为0.179;图 10(f)显示了X2.64040台站获取的102次有效测量,其ZH比平均值为0.816,标准方差为0.107。
|
图 10 天然地震激发的16s的瑞利面波在2个台站上的ZH比 (a)X2.15605台站记录到的天然地震激发的16s瑞利面波在径向R和垂向Z方向上的归一化波形,图上部列出了该地震发生时刻、震级及震中与X2.15065间的距离;(b)X2.15605台站记录到的瑞利面波的偏振图像;(c)利用周边发生的632个地震测量得到的16s瑞利面波在台站X2.15065的ZH比分布;图(d)、(e)、(f)同图(a)、(b)、(c),记录台站为X2.64040 |
对比图 8、9、10可知,就16s周期的瑞利面波而言,我们从九分量NCF以及天然地震中中获取的ZH比具有很强的一致性,这表明了利用云计算方法获得的九分量NCF中波形相对振幅的可靠性。同时,2个台站同周期瑞利面波的ZH比具有明显差异。对比图 1可以看出,X2.15065台站位于丘陵山地,而X2.64040台站位于宁夏沉积盆地区域,二者ZH比的差异反映了台站下方不同的横波特征。由于本文重点为海量NCF的云计算实现及其验证,利用获取的ZH比反演浅部横波结构将另文阐述。
4 结论地震学是以观测为基础的学科,地震学研究的很多突破都与观测资料的增加和观测质量的提高有很大关系。最近10年来,地震观测资料的数量呈现了爆发性的增长,在给我们带来海量数据的同时,也对地震学中的传统计算模式提出了挑战。
背景噪声的互相关计算是一种典型的数据密集型计算,其计算总量随着观测台站数目的增多和观测持续时间的增加而呈非线性的增长。然而,密集台站间的噪声互相关函数又是对观测区域进行高精度成像的重要数据。为了解决传统计算模式遇到的瓶颈,本文提出了一种基于云计算的九分量噪声互相关函数计算方法。该方法利用现代云计算技术所提供的弹性的、可扩充的存储、计算能力,实现了海量数据集合下九分量噪声互相关的计算。
我们将该技术应用于“中国地震科学台阵探测——南北地震带北段”674个宽频带台站2014~2015年的三分量连续记录,获取了所有台站间的九分量噪声互相关函数。计算结果表明,获取22万条路径上2年的噪声互相关函数平均耗时约为10.2h,相比传统计算方法具有接近400倍的加速效能。通过对计算得到的九分量NCF中瑞利面波振幅ZH比的测量以及地震记录中相应面波ZH的对比分析,验证了九分量NCF计算结果的可靠性。
地震学研究已经开始进入大数据时代,本文是对现代云计算技术在传统地震学研究中应用的初步探索,其研究结果可为后续相关研究提供参考。通过云计算技术获得的海量NCF数据,也可作为后续地震学研究的重要数据支撑。
致谢: 感谢中国地震科学探测台阵数据中心提供的波形数据。| 刘志坤, 黄金莉. 2010, 利用背景噪声互相关研究汶川地震震源区地震波速度变化. 地球物理学报, 53(4): 853–863. |
| 徐义贤, 罗银河. 2015, 噪声地震学方法及其应用. 地球物理学报, 58(8): 2618–2636. DOI:10.6038/cjg20150803 |
| Bao X, Sun X, Xu M, et al. 2015, Two crustal low-velocity channels beneath SE Tibet revealed by joint inversion of Rayleigh wave dispersion and receiver functions. Earth Planet Sci Lett, 415: 16–24. DOI:10.1016/j.epsl.2015.01.020. |
| Bensen G D, Ritzwoller M H, Barmin M P, et al. 2007, Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements. Geophys J Int, 169: 1239–1260. DOI:10.1111/gji.2007.169.issue-3. |
| Brenguier F, Campillo M, Hadziioannou C, et al. 2008, Postseismic relaxation along the San Andreas Fault at Parkfield from continuous seismological observations. Science, 321(5895): 1478. DOI:10.1126/science.1160943. |
| Campillo M, Roux P. 2015, Crust and lithospheric structure-seismic imaging and monitoring with ambient noise correlations. Treatise on Geophysics: 391–417. |
| Chong J, Ni S, Zhao L. 2015, Joint inversion of crustal structure with the Rayleigh wave phase velocity dispersion and the ZH ratio. Pure Appl Geophys, 172(10): 1–16. |
| Heilmann Z, Deidda G P, Satta G, et al. 2013, Real-time imaging and data analysis for shallow seismic data using a cloud-computing portal. Near Surface Geophysics, 11(4): 407–421. |
| Li G, Chen H, Niu F, et al. 2016, Measurement of rayleigh wave ellipticity and its application to the joint inversion of high-resolution S wave velocity structure beneath northeast China. J Geophys Res, 121: 864–880. DOI:10.1002/2015JB012459. |
| Lin F C, Ritzwoller M H, Yang Y, et al. 2011, Complex and variable crustal and uppermost mantle seismic anisotropy in the western United States. Nat Geosci, 4(1): 55–61. DOI:10.1038/ngeo1036. |
| Lin F C, Tsai V C, Schmandt B. 2014, 3-D crustal structure of the western United States:application of Rayleigh-wave ellipticity extracted from noise cross-correlations. Geophys J Int, 198(2): 656–670. DOI:10.1093/gji/ggu160. |
| Magana-Zook S, Gaylord J M, Knapp D R, et al. 2016, Large-scale seismic waveform quality metric calculation using Hadoop. Comput Geosci, 94: 18–30. DOI:10.1016/j.cageo.2016.05.012. |
| Riahi N, Gerstoft P. 2016, Using graph clustering to locate sources within a dense sensor array. Signal Processing, 132: 110–120. |
| Shapiro N M, Campillo M, Stehly L, et al. 2005, High resolution surface wave tomography from ambient seismic noise. Science, 307: 1615–1618. DOI:10.1126/science.1108339. |
| Tomar G, Shapiro N M, Mordret A, et al. 2017, Radial anisotropy in Valhall:ambient noise based studies of Scholte and Love waves. Geophys J Int, 208(3): 1524–1539. DOI:10.1093/gji/ggw480. |
| Wang L Z, Laszewski G, Younge A, et al. 2010, Cloud computing:A perspective study. New Gener Comput, 28(2): 137–146. DOI:10.1007/s00354-008-0081-5. |
| Wapenaar K. 2004, Retrieving the elastodynamic Green's function of an arbitrary inhomogeneous medium by cross correlation. Phys Rev Lett, 93(25): 254301. DOI:10.1103/PhysRevLett.93.254301. |
| Yano T, Tanimoto T, Rivera L. 2009, The ZH ratio method for long-period seismic data:inversion for S-wave velocity structure. Geophys J Int, 179(1): 413–424. DOI:10.1111/gji.2009.179.issue-1. |
| Yao H, Beghein C, Hilst R D V D. 2008, Surface wave array tomography in SE Tibet from ambient seismic noise and two-station analysis-Ⅱ. Crustal and upper-mantle structure, Geophys J Int, 173(1): 205–219. |
| Yoon C E, Ossian O, Bergen K J, et al. 2015, Earthquake detection through computationally efficient similarity search. Sci adv, 1(11): e1501057. DOI:10.1126/sciadv.1501057. |
| Zha Y, Webb S C, Menke W. 2013, Determining the orientations of ocean bottom seismometers using ambient noise correlation. Geophys Res Lett, 40(14): 3585–3590. DOI:10.1002/grl.50698. |
| Zheng Y, Shen W, Zhou L, et al. 2011, Crust and uppermost mantle beneath the North China Craton. northeastern China, and the Sea of Japan from ambient noise tomography, J Geophys Res, 116: B12312. DOI:10.1029/2011JB008637. |
| Zinno I, Elefante S, Luca C D, et al, 2015, New advances in intensive DInSAR processing through cloud computing environments//Geoscience and Remote Sensing Symposium, IEEE, 5264~5267. |
 2018, Vol. 34
2018, Vol. 34



