2. 天津大学水利工程仿真与安全国家重点实验室, 天津市南开区卫津路92号 300072;
3. 国家海洋局南海维权技术与应用重点实验室, 广州市新港中路353号 510310;
4. 水沙科学与水灾害防治湖南省重点实验室, 长沙市天心区万家丽南路2 段960号 410114
2. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China;
3. Key Laboratory of Technology for Safeguarding of Maritime Rights and Interests and Application, SOA, Guangzhou 510310, China;
4. Key Laboratory of Water-sediment Sciences and Water Disaster Prevention of Hunan Province, Changsha 410004, China
海啸是由水下地震、火山爆发、水下塌陷及滑坡等大地活动或气象变化产生的破坏性海浪,其中,由水下地震产生的地震海啸较为普遍,表现为海底地形急剧升降变动引起的海水强烈扰动。根据海啸传播至岸边时间的长短,它可分为近海地震海啸和远洋地震海啸。海啸的发生频率虽然较低,可一旦发生,破坏力是巨大的。2004年12月26日印度尼西亚苏门答腊岛西北附近海域发生了MW9.1强烈地震,地震在印度洋沿岸引发罕见的地震海啸并传播到全球各大洋(Yeh et al,2007)。2011年3月11日日本东北部海域发生了MW9.0强烈地震,这是日本近海发生的最强烈的一次大地震,并引发了太平洋范围的海啸(王培涛等,2012)。据统计,每2年全球发生1次局地破坏性海啸,每10年发生1次越洋大海啸(于福江等,2011)。Jing等(2013)研究发现,地震引发海啸的概率很高,而在过去约100年里,震级≥8.8的地震都触发了海啸。
我国处于太平洋西部,海区辽阔,海岸线长达18000km,近海海域大多位于环太平洋地震带上,历史上地震海啸时有发生,是世界上最早记录到地震海啸的国家。据不完全统计,公元47~2004年,中国沿海共发生29次地震海啸,其中,8~9次为破坏性海啸。虽然自1949年新中国成立以来我国并未发生破坏性海啸,但近期南海地震频发,一旦诱发海啸将给我国南部、东南部发达城市造成巨大损失(包澄澜等,2005;杨马陵等,2005;Liu et al,2007)。我国历史上曾经发生过多次海啸,其中,台湾地区周围是海啸的高发区域,其次是大陆架区域,低发区是渤海区域。在各省份中,按照有历史记录的海啸分析,浙江的发生次数最多,高达45次,其次是江苏、山东、上海、福建、台湾、广东。按照已确定的海啸记录分析,台湾发生的次数最多,有8次,其次是山东、广东和浙江。不论哪个数据都表明,我国是一个海啸发生的危险区,而南海区域是中国受海啸威胁最大的地方,这是因为吕宋岛西侧和马尼拉海沟一带是地震活跃带(潘文亮等,2009)。Li等(2016)认为,常用的均匀滑动模型明显低估了海啸灾害。因此,研究建立广东沿海海啸预警机制,在海啸发生后迅速预报海啸到达时间、海啸最大波高,可为海啸防灾减灾提供有力支持,以期最大化地减少海啸造成的损失。
现有的海啸计算模式中,一般不含有潮汐模块。这是由于通常不考虑潮汐与海啸的非线性作用,将计算出的海啸波高与潮位值进行线性叠加来得到关心站点的水位。但是,对于近岸浅水域,潮汐与海啸的非线性作用会明显增大,故影响海啸波的波幅及到达时间。本文利用COMCOT模型和全球潮汐模式TPXO7.2,建立广东沿海天文潮与海啸的耦合数学模型,针对马尼拉地震带海啸,通过设计海啸震源计算,分析广东省沿海海啸风险。
1 数值模型COMCOT模型(Cornell Multi-grid Coupled Tsunami model)是由Cornell大学土木与环境工程系Philip Liu研究组开发基于浅水长波方程的海啸数值计算模式,该模式已被多次用来模拟历史海啸事件,如1992年印度尼西亚Flores Islands海啸(Liu et al,1995)、2003年Algeria海啸(Wand et al,2005)、2004年印度洋大海啸(Wand et al,2006)以及2011年日本海啸(应超等,2015;Jing et al,2012),均有效模拟了海啸生成、传播、爬高和淹没的整个过程。模式可根据研究范围,灵活选择球面与直角坐标系下的线性与非线性浅水方程,所有方程均采用显式蛙跳有限差分法进行离散。
1.1 基本方程球坐标下,考虑科氏力忽略海底摩擦,线性浅水方程为
| $ \frac{\partial \mathit{\eta }}{\partial \mathit{t}}\text{+}\frac{\text{1}}{\mathit{R}\text{cos}\phi }\left[ \frac{\partial \mathit{P}}{\partial \mathit{\psi }}+\frac{\partial }{\partial \phi }\text{(cos}\mathit{\varphi Q}\text{)} \right]\text{=0} $ | (1) |
| $ \frac{\partial \mathit{P}}{\partial \mathit{t}}\text{+}\frac{\text{g}\mathit{H}}{\mathit{R}\text{cos}\phi }\cdot \frac{\partial \mathit{\eta }}{\partial \mathit{\psi }}\text{-}\mathit{fQ}\text{=0} $ | (2) |
式中,η为相对于平均海平面的自由表面位移;R为地球半径;H=η+h为总的水深,h为静水深;P为沿纬度单位宽度的通量;Q为沿经度单位宽度的通量;ϕ、ψ分别为经度和纬度;f为科氏力系数;g为重力加速度。海啸传播至近岸,采用笛卡尔坐标下非线性浅水波方程,并考虑底摩擦效应,其连续方程和动量方程为
| $ \frac{\partial \mathit{\eta }}{\partial \mathit{t}}+\frac{\partial \mathit{P}}{\partial \mathit{x}}+\frac{\partial \mathit{Q}}{\partial \mathit{y}}=0 $ | (3) |
| $ \frac{\partial \mathit{P}}{\partial \mathit{t}}\text{+}\frac{\partial }{\partial \mathit{x}}\left(\frac{{{\mathit{P}}^{\text{2}}}}{\mathit{H}} \right)\text{+}\frac{\partial }{\partial \mathit{y}}\left(\frac{\mathit{PQ}}{\mathit{H}} \right)\text{+}\mathit{gH}\frac{\partial \mathit{\eta }}{\partial \mathit{x}}\text{+}\frac{\mathit{g}{{\mathit{n}}^{\text{2}}}}{{{\mathit{H}}^{\text{7/3}}}}\mathit{P}{{\text{(}{{\mathit{P}}^{\text{2}}}\text{+}{{\mathit{Q}}^{\text{2}}}\text{)}}^{\text{1/2}}}\text{=0} $ | (4) |
| $ \frac{\partial \mathit{Q}}{\partial \mathit{t}}\text{+}\frac{\partial }{\partial \mathit{y}}\left(\frac{{{\mathit{Q}}^{\text{2}}}}{\mathit{H}} \right)\text{+}\frac{\partial }{\partial \mathit{x}}\left(\frac{\mathit{PQ}}{\mathit{H}} \right)\text{+}\mathit{gH}\frac{\partial \mathit{\eta }}{\partial \mathit{x}}\text{+}\frac{\mathit{g}{{\mathit{n}}^{\text{2}}}}{{{\mathit{H}}^{\text{7/3}}}}\mathit{Q}{{\text{(}{{\mathit{P}}^{\text{2}}}\text{+}{{\mathit{Q}}^{\text{2}}}\text{)}}^{\text{1/2}}}\text{=0} $ | (5) |
式中,P、Q分别为x和y方向上的体积通量;n为曼宁粗糙系数。
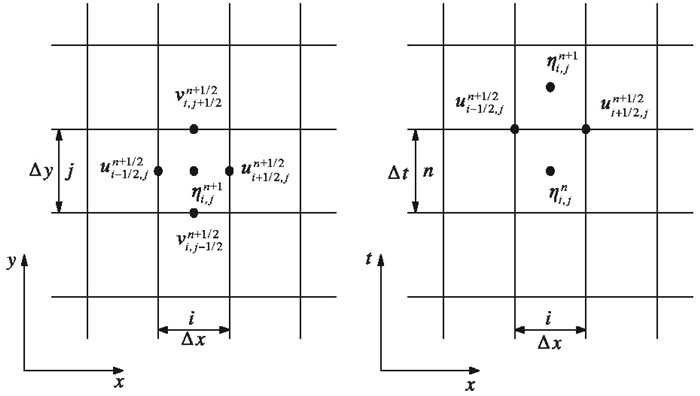
1.2 数值格式对式(1)~(5)采用了蛙跳有限差分格式进行离散,非线性对流项采用迎风向上格式离散。图 1为交错格式示意图。由图 1可见,波高和体积通量在空间和时间上都是交错的,波高及水深位于网格中心,体积通量位于网格线上。数值格式的截断误差为o(Δx2,Δy2,Δt2),在时空上均有二阶精度。COMCOT是比较成熟的海啸数值模型,具体算法详见文献(Wang,2009)。
|
图 1 交错格式示意图 左为空间上;右为时间上 |
海啸初始条件的确定是通过输入地震断层参数,由弹性断层模型计算得到。模式中可选择Mansinha和Smylie的弹性半空间错移模型和Okada的理论模型,这也是现阶段常用的2种弹性断层模型。弹性断层模型基于弹性错移理论建立,主要利用断层错动资料计算特定点处的位移量。例如,断层在j方向上错动Δui,对整个矩形断层范围积分,即得到
| $ {{\mathit{u}}_{\mathit{i}}}\text{=}\int\limits_{\sum }{\text{ }\!\!\Delta\!\!\text{ }{{\mathit{u}}_{\mathit{j}}}}\left[ \mathit{\lambda }{{\mathit{\delta }}_{\mathit{jk}}}\frac{\partial \mathit{u}_{\mathit{i}}^{\mathit{l}}}{\partial {{\mathit{\zeta }}_{\mathit{l}}}}\text{+}\mathit{\mu }\left(\frac{\partial \mathit{u}_{\mathit{i}}^{\mathit{j}}}{\partial {{\mathit{\zeta }}_{\mathit{k}}}}\text{+}\frac{\partial \mathit{u}_{\mathit{i}}^{\mathit{k}}}{\partial {{\mathit{\zeta }}_{\mathit{j}}}} \right) \right]{{\mathit{v}}_{\mathit{k}}}\text{d}\sum $ | (6) |
式中,δjk为克罗内克函数变量;vk为Σ面向外的垂直向量;μ、λ为拉梅常数;uij为受到破裂面在j方向的单位应力作用而在地表i方向产生的位移。
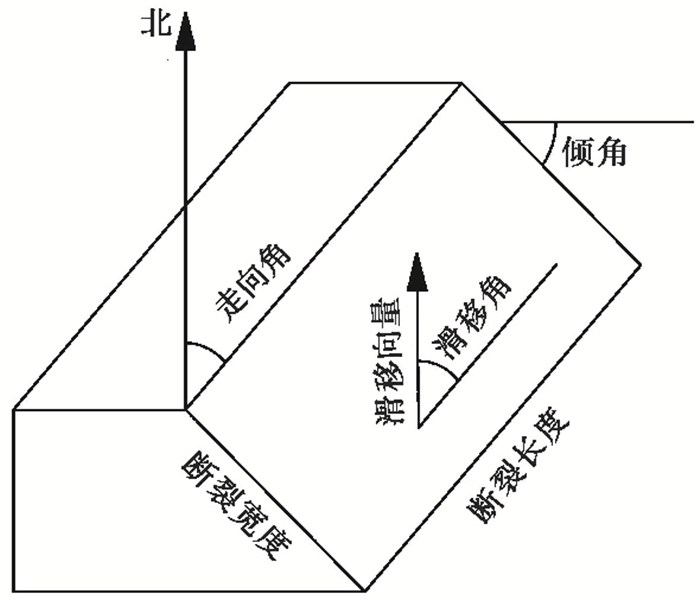
COMCOT模型中的断层模型共输入9个参数,分别为震中经度、纬度、震源深度、断裂长度、断裂宽度、滑动量、走向角、倾角、滑移角。断层模型示意图见图 2。
|
图 2 断层示意图 |
边界条件的设定中,水边界设为开边界。选择线性浅水波方程时,海陆边界设为垂直反射边界;选择非线性浅水波方程时,采用移动边界方案,即考虑岸滩的干湿变化。本文通过源码修改在模型中加入潮汐强迫边界条件(李林燕等,2012;赵鑫等,2016),外海潮位边界由全球潮汐模型(TPXO7.2)求得,该模型通过10个分潮推算天文潮位,包含8个主要分潮M2、S2、K1、O1、N2、P1、K2、Q1以及2个长周期分潮Mf和Mn,基本能够构造出外海深水处真实的天文潮过程
| $ {{\mathit{\zeta }}_{\text{0}}}\left(\mathit{x} \right)\text{=}{{\mathit{\zeta }}_{\mathit{p}}}\left(\mathit{x} \right)\text{+}\sum\limits_{\mathit{i}\text{=1}}^{10}{{{\mathit{A}}_{\mathit{i}}}\left(\mathit{x} \right)}\cdot \text{sin }\!\![\!\!\text{ }{{\mathit{\omega }}_{\mathit{i}}}\mathit{t}\text{+}{{\mathit{\alpha }}_{\mathit{i}}}\left(\mathit{x} \right)\text{ }\!\!]\!\!\text{ } $ | (7) |
式中,ζ0为边界处的潮位;ζp为边界处静压水位;i为1~10,分别对应上述分潮;Ai、αi分别为分潮在3条边界处的振幅和迟角;ωi为分潮的角频率。
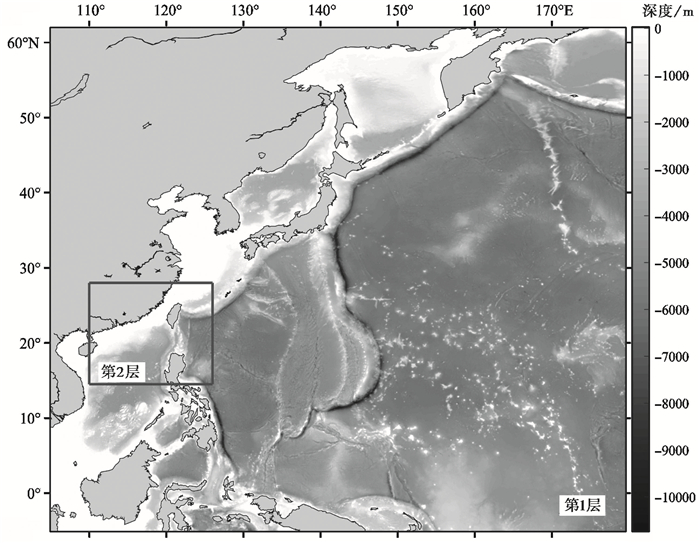
2 海啸模型验证 2.1 计算区域与网格布置利用日本“311”海啸对COMCOT模型进行验证。模型采用2层嵌套网格,第1层网格的范围是5°S~62°N、105.0°~179.5°E,计算范围包括东海、台湾海峡、南中国海、日本及部分西太平洋海域,网格大小为4′,控制方程选择球坐标下的线性浅水长波方程,忽略摩擦作用;第2层网格的范围是14.5°~28.0°N、110°~126°E,网格大小为0.8′(图 3)。
|
图 3 网格范围 |
日本“311”地震海啸发生后,Tang等(2012)利用D21418浮标站在震后0.42~0.58h和D21401在0.80~1.23h之间的监测数据,反演出初始海面位移有10m的抬升和3m的下沉,震源可由6块沿着日本海沟的100km×50km的单位震源组合而成,在海啸到岸前5h计算出了美国海岸线30多个城市的海啸波爬高和淹没情况,模拟值与后来的观测值较为符合。Wei等(2013)也利用同样的断层设置,模拟计算了海啸在日本近岸的爬高和淹没,结果表明,模拟计算的茨城县和青森县的淹没范围准确率达到85.5%。以上述National Oceanic and Atmospheric Administration的断层设置作为海啸模型的输入条件,模拟此次海啸波的产生和传播,并输出在日本近岸的DART浮标点以及我国近海验潮站的波高序列。地震断层参数设计见表 1。
| 表 1 地震断层参数 |
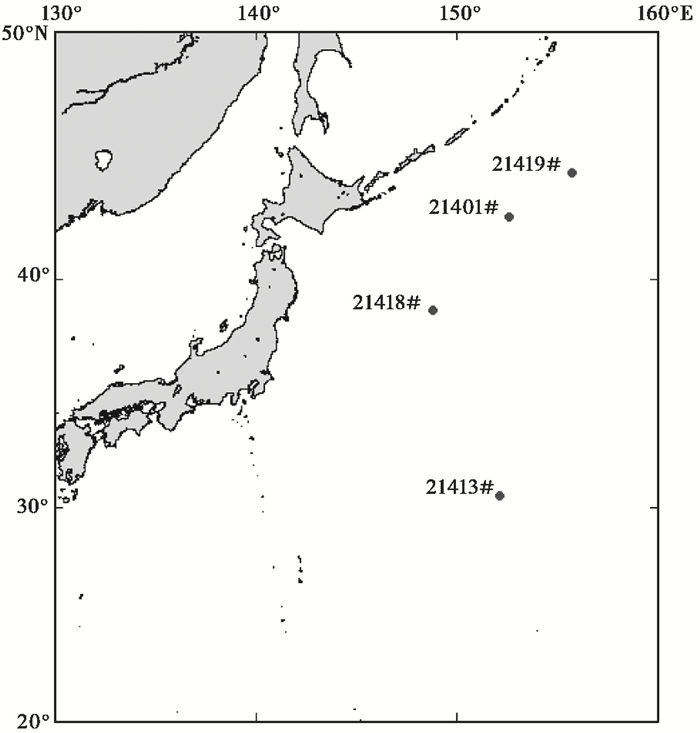
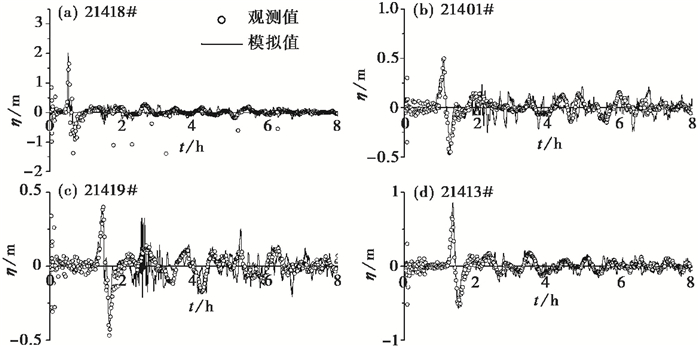
本研究收集海啸发生后日本东部编号为21401#(42.617°N,152.583°E)、21413#(30.515°N,152.117°E)、21418#(38.688°N,148.769°E)、21419#(44.455°N,155.736°E)的海啸浮标站水位资料进行验证,浮标分布如图 4所示,模型验证如图 5所示。在4个浮标点处,首波到岸时间的模拟值与观测值之差均小于2min,21401#和21419#浮标站,波高的模拟值与观测值之差小于2cm,浮标点处的模拟值与实测值较为符合;在21418#h和21413#浮标站,波高的计算值与观测值的误差分别为36、21cm,误差相对较大,这与海底地形误差、验潮站局部海浪初值累积误差等有关。
|
图 4 日本东部海啸浮标分布 |
|
图 5 浮标点处模拟值与观测值对比 |
在我国南海海域附近,3大俯冲带被认为具有地震激发海啸的潜在危险,分别为马尼拉俯冲带、琉球群岛俯冲带和北苏拉威西岛俯冲带。马尼拉海沟位于亚欧大陆板块和菲律宾海板块交界处,南起菲律宾巴拉望岛北端,沿菲律宾吕宋西部边缘向北发展,北至台湾岛,总长度约1000km。亚欧大陆板块以70mm/a的速度向菲律宾海板块之下俯冲,俯冲板块与上覆板块之间的汇聚挤压作用持续了相当长的一段时间,当集聚的应力释放,便会发生海底地震,地震激发的海啸波会使台湾、福建、广东、海南等沿海地区毫无遮拦地暴露在海啸波的威胁之下。
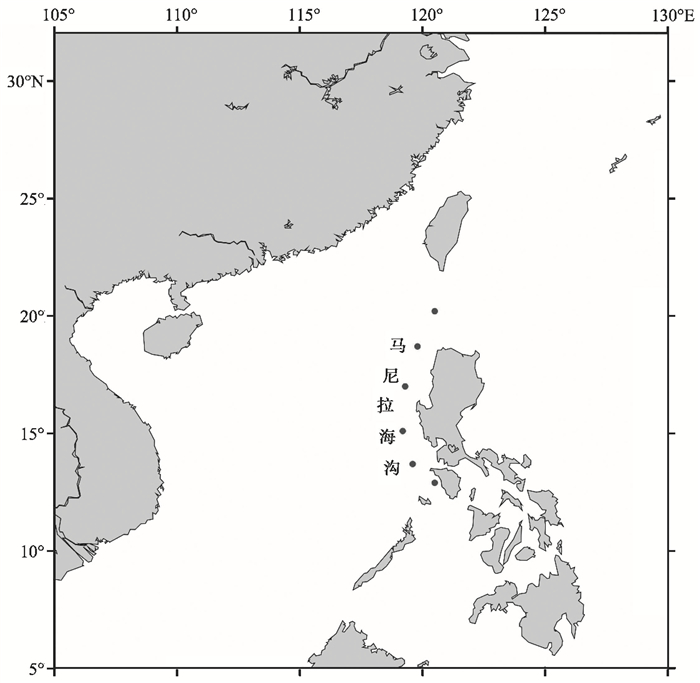
本文通过使用COMCOT模型模拟了马尼拉海沟地震后产生的海啸对广东省附近海域的影响,模型采用2层嵌套网格,网格范围如图 5所示。美国地质调查局根据海沟方位角和断层几何学将马尼拉海沟分为6个断裂带,震源位置如图 6所示,地震震级为MW9.3(Phuong et al,2013),震源断层参数见表 2。
|
图 6 马尼拉海沟断裂带位置 |
| 表 2 马尼拉海沟断层参数 |
图 7为马尼拉海沟发生地震后海啸波传播和先导波到达时间图。马尼拉海沟因地震引发的海啸波3h之后传播到广东省沿岸海域附近。COMCOT可以得到外海岛屿附近海域更精细的模拟结果,由COMCOT第2层模型结果可以得到广东省附近海啸引发的最大增水值。

|
图 7 马尼拉海沟地震海啸波传播及先导波到达时间 |
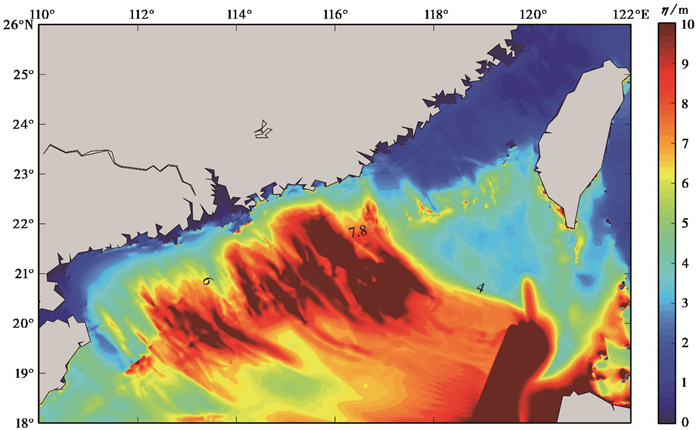
图 8为马尼拉海沟地震引发的海啸对广东省附近海域影响的最大增水图。由图 8可知,马尼拉海沟处地震引发的海啸由深海区传入浅水区后,在浅水效应的作用下,在东沙群岛附近海啸波有明显的增高,最大增水达到11.95m,海啸波传到广东省沿岸后最大增水约为4.87m。海啸波的速度近似为(gH)1/2,当海啸波与高潮位重合时,耦合计算总水深H增大,海啸传播速度增大,传播时间变短。若不考虑潮汐、海啸的计算结果,在时间上会有所延迟,约15min左右,沿海各地受地形的影响,会略有不同。表 3为在马尼拉海沟地震影响下广东各海洋站增、减水值及对应时间。
|
图 8 马尼拉海沟地震引发的海啸对广东省沿岸海域最大增水图 |
| 表 3 在马尼拉海沟地震影响下广东各海洋站增、减水值及对应时间 |
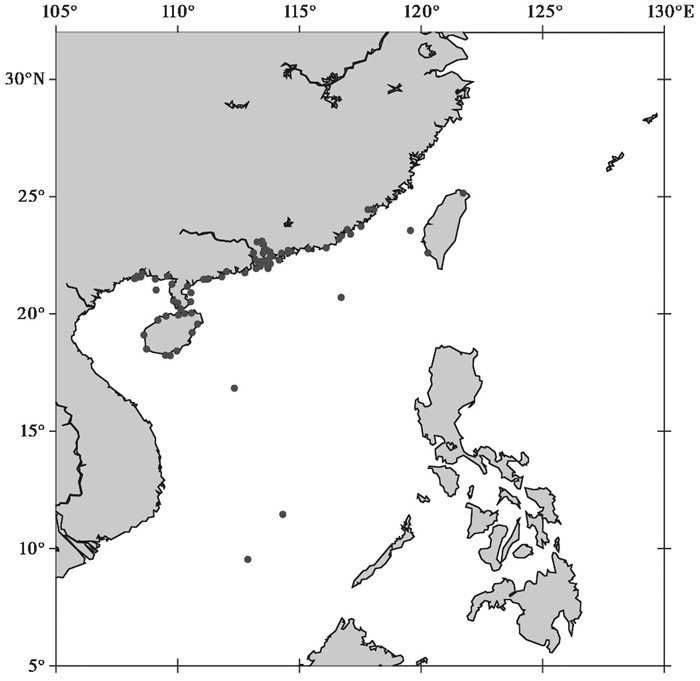
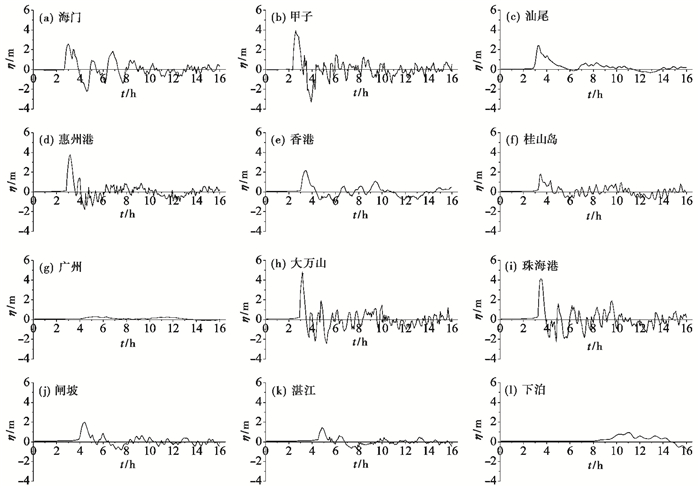
为了更加详细地了解海啸波对广东省沿岸的影响,选取广东省沿岸的海门、甲子、汕尾、惠州港、香港、桂山岛、广州、大万山、珠海港、海陵山岛(闸坡)、湛江、下泊等处,得到其水位随时间的变化序列,从而分析海啸波对广东省沿岸海域的影响。敏感点位置见图 9,受影响的时间序列见图 10。在各海洋站的统计中,东沙岛和大万山的最大增水相对较为显著,分别为11.95、4.87m;其次是在珠海港和甲子附近,最大增水达到4m左右,惠州港附近3.76m,海门、汕尾、井岸、香港最大增水为2.0~2.5m,海陵山岛(闸坡)、汕头、茂石化(水东港)、东澳岛、桂山岛、西葛、潮州港(三百门)最大增水为1.5~2.0m,大鹏湾(盐田港)、大亚湾、湛江、南澳岛(云澳湾)、马鞭洲(广石化)、横山、三灶岛、灯笼山、流沙最大增水为1.0~1.5m;随后较弱的为乌石、下泊、下港、博贺、电白、硵洲岛(北港)、北津、海安,最大增水为0.5~1.0m;澳门、珠海(九洲港)、内伶仃岛、黄埔、横门、珠海(香洲)、北街、南沙(水牛头)、广州、海沁、深圳机场(油码头)、上川岛(三洲湾)、舢舨洲、蛇口(赤湾)最大增水为0.19~0.50m,相对稍弱。由图 10可知,马尼拉海沟地震引发的海啸约2.5h后到达广东沿岸,海啸波到达敏感点区附近后,影响在1h内达到最大,随后影响逐渐变小。内伶仃洋因外海星罗棋布的岛屿阻拦和浅水地形影响,受海啸波的影响微弱,海啸波高相对较小。不到5h,最大增水覆盖了广东大部分沿海地区,而对于广州、湛江以西的影响则较为微弱。
|
图 9 站位示意图 |
|
图 10 马尼拉海沟地震后典型站位水位时间序列 |
本文基于COMCOT模型建立了广东沿海天文潮与海啸耦合数学模型,对日本“311”海啸进行了良好地验证,同时模拟了马尼拉海沟地震后产生的海啸对广东附近海域的影响,对广东沿岸由东向西的海洋站(海门至下泊等处)数据进行了分析,主要研究结果如下。
(1) 本文建立的海啸耦合数学模型能够较好地模拟日本“311”海啸,首波到岸时间的模拟值与观测值之差均小于2min,波高的计算结果与实测值对比良好,两者的差异与海底地形误差、验潮站局部海浪初值累积误差等有关。本模型为准确评估马尼拉海沟地震后产生的海啸对广东沿海的影响提供了研究基础。
(2) 马尼拉海沟地震引发的海啸约2.5h后到达广东沿岸,海啸波到达敏感点区附近后,影响在1h内达到最大,随后影响逐渐变小。内伶仃洋因外海星罗棋布的岛屿阻拦和浅水地形影响,受海啸波的影响微弱,海啸波高相对较小。
(3) 基本上5h以内,最大增水覆盖了广东大部分沿海地区,对近海工程将造成影响。东沙岛和大万山的最大增水相对较为显著,分别为11.95、4.87m;其次是在珠海港和甲子附近最大增水达到4m左右,惠州港附近3.76m,海门、汕尾、井岸、香港最大增水为2.0~2.5m。而对于广州,湛江以西的影响则较为微弱。
(4) 由于南海海啸发生的历史记录尚少,地震数据亦有所欠缺,震源机制解不能有效精确,故计算时间段无法准确判定。线性叠加潮汐则比耦合潮汐的海啸波计算结果稍安全。同时,潮汐对海啸的影响叙述篇幅太长,这也是后续的研究工作,海啸波抵达时间并无多大差异,主要差异体现在海啸最大波高,将来可考虑多年最大、最小潮差时间段,一年当中不同月份的最大、最小潮差时间段,以及受到东北季风和西南季风影响,甚至受到极端天气影响情况下的模拟,以构建相应的海啸源数据库,建立更加完善的南海海啸耦合数学模型。
| 包澄澜, 叶琳. 2005, 海啸灾害与预警. 海洋预报, 22(1): 1–4. DOI:10.11737/j.issn.1003-0239.2005.01.001 |
| 李林燕, 毛献忠. 2012, 深圳海域潮汐海啸波耦合数值研究. 海洋学报, 34(3): 11–18. |
| 潘文亮, 王盛安, 蔡树群. 2009, 南海潜在海啸灾害的数值模拟. 热带海洋学报, 28(6): 7–14. DOI:10.11978/j.issn.1009-5470.2009.06.007 |
| 王培涛, 于福江, 赵联大, 等. 2012, 2011年3月11日日本地震海啸越洋传播及对中国影响的数值分析. 地球物理学报, 55(9): 3088–3096. DOI:10.6038/j.issn.0001-5733.2012.09.026 |
| 杨马陵, 魏柏林. 2005, 南海海域地震海啸潜在危险的探析. 灾害学, 20(3): 41–47. |
| 应超, 于普兵, 穆锦斌, 等. 2015, 东海海啸反问题预报模式研究——以日本"3. 11"海啸为例.海洋预报, 32(3): 36–42. |
| 于福江, 原野, 赵联大, 等. 2011, 2010年2月27日智利8.8级地震海啸对我国影响分析. 科学通报, 56(1): 1–8. |
| 赵鑫, 应超, 孙志林. 2016, 天文潮与海啸耦合数学模型研究——以东中国海温州湾为例. 海洋学研究, 34(2): 11–17. |
| Jing H M, Zhang H, Wu Z L, et al. 2012, Numerical simulation of March 11, 2011 Honshu, Japan tsunami. Chinese Science Bulletin, 57(27): 3617–3622. DOI:10.1007/s11434-012-5229-5. |
| Jing H M, Zhang H, Yuen D A, et al. 2013, A revised evaluation of tsunami hazards along the Chinese coast in view of the Tohoku-Oki earthquake. Pure Appl Geophys, 170(1): 129–138. DOI:10.1007/s00024-012-0474-8. |
| Li L, Switzer A D, Chan C H, et al. 2016, How heterogeneous coseismic slip affects regional probabilistic tsunami hazard assessment:A case study in the South China Sea. J Geophys Res, 121(8): 6250–6272. DOI:10.1002/2016JB013111. |
| Liu P L F, Cho Y S, Briggs M J, et al. 1995, Runup of solitary waves on a circular island. J Fluid Mech, 302: 259–285. DOI:10.1017/S0022112095004095. |
| Liu Y, Santos A, Wang S M, et al. 2007, Tsunami hazards along Chinese coast from potential earthquakes in South China Sea. Phys Earth Planet Inter, 163(1): 233–244. |
| Phuong N H, Phuong V H, Truyen P T, et al. 2013, Simulation of worst case tsunami scenario from the manila trench using the COMCOT model. Vietnam Journal of Marine Science & Technology, 13(4): 307–316. |
| Tang L, Titov V V, Bernard E N, et al. 2012, Direct energy estimation of the 2011 Japan tsunami using deep-ocean pressure measurements. J Geophys Res, 117(C8): 72–82. |
| Wand X, Liu P L F. 2005, A numerical investigation of Boumerdes-Zemmouri(Algeria)earthquake and Tsunami. Cmes Computer Modeling in Engineering & Ences, 10(2): 171–183. |
| Wand X, Liu P L F. 2006, An analysis of 2004 Sumatra earthquake fault plane mechanisms and Indian Ocean tsunami. Journal of Hydraulic Research, 44(2): 147–154. DOI:10.1080/00221686.2006.9521671. |
| Wang X, 2009, User manual for Comcot version 1. 7(first draft), New York: Cornel University. |
| Wei Y, Chamberlin C, Titov V V, et al. 2013, Modeling of the 2011 Japan tsunami:Lessons for near-field forecast. Pure Appl Geophys, 170(6-8): 1309–1331. DOI:10.1007/s00024-012-0519-z. |
| Yeh H, Francis M, Peterson C, et al. 2007, Effects of the 2004 great Sumatra tsunami:southeast Indian coast. Journal of Waterway Port Coastal & Ocean Engineering, 133(6): 382–400. |
 2018, Vol. 34
2018, Vol. 34


