2. 福州大学, 福州 350108
2. Fujian Earthquake Agency, Fuzhou 350003, China
地震学是通过研究地震产生的地震波从而推断地球内部结构和地震发生的物理机制的科学(Shearer,1999;Bondar,2004)。它是人类了解无法直接到达的地球内部的一种重要方法和手段。由于天然地震的震源位置和发震时间无法控制,常常导致射线的几何分布不够理想,这给获得研究区域地下结构的良好反演解造成了相当的困难(张先康等,1994)。利用人工震源激发产生地震波的反演方法,可以在研究区域建立相对较完备的观测系统,在很大程度上弥补了天然地震的这一不足。多年来,福建省地震局一直采用华南地区地壳速度模型对周边的地震事件和爆破进行定位分析,但是,一旦模型不合适或有较大偏差将会对日常地震编目工作造成重大影响,因此,很有必要对华南地壳速度模型进行检验。在通常的地震反演中,地震发震时刻、震源位置等信息无法准确得知,故缺乏对华南速度模型进行检验的必要条件。然而,福建地区的多次人工爆破实验为我们提供了一个良好契机(廖其林等,1988),利用爆破实验准确的发震时间、发震位置可以获得不同震相的精确到时,进而对华南速度模型进行检验,同时,在此基础上提出华南速度模型的修正意见。
1 研究背景在地震观测台站确定的情况下,影响地震定位精度的主要因素包括结构模型的误差和观测走时等信息误差(陈棋福等,2001)。恰当的震源精定位方法可通过应用良好的速度模型提高定位结果的可信度,同样地,也可以运用不同的精定位方法,通过比较定位结果来判断速度模型的优劣(赵仲和,1983)。一维参考地震波速度模型是区域地震构造研究的重要基础(陈祥熊等,2005),三维成像反演的可靠性即有赖于一维模型的准确建立。另一方面,基于一维速度模型的计算相对于基于三维速度模型的计算,在精度允许的范围内具有低成本、高效率等优势。因此,一维速度结构的研究依然是当前地下速度结构研究的重点之一(孙安辉等,201l)。
福建测震台网在2010年共有33个区域台和8个水库台,平均台间距56km,至2011年“十一·五”福建地震烈度速报台网建成后,又增加了44个地方台,现福建测震台网共由85个台组成了较为密集的地震台网,平均台间距为31km左右(图 1)。
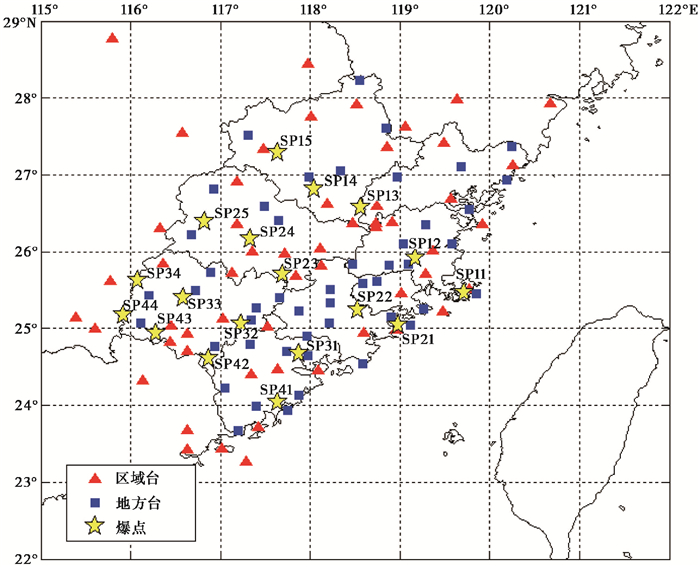
|
图 1 炮点与台网分布 |
2010~2012年福建省地震局联合中国地震局物探中心在福建区域开展“福建及台湾海峡地壳深部构造探测实验”项目,项目成功实施了18次爆破实验,爆破的炮点位置基本覆盖福建省大部分地区(图 1)。这些爆破都有精确的时间、经纬度、用药量及地名等炮点参数(表 1),本文利用福建测震台网记录到的数字地震波形分别对这些爆破事件进行震中位置的确定,利用得到的结果与准确的爆破点位置进行对比,并对测震台网常用的4种定位方法进行定位精度判定,最后结合这些资料来检验福建华南速度模型。
| 表 1 18次爆破炮点信息 |
福建测震台网记录到了18次爆破的完整波形,所有爆破均有多个台站记录,记录台站数为22~101个,最多的是SP11爆点,101个台;最少的是SP33爆点,22个台。其中,2010年激发的4个炮点(SP31~SP34)只使用了41个台,记录台数较少。爆破激发波的最远传播200~352km,其中,SP11爆点352km。爆破激发了清晰的直达纵波Pg震相、莫霍面反射波PmP震相和SmS震相,在震中距120km处出现了明显的来自莫霍界面的首波震相Pn,近台还记录到短周期面波震相,由于直达横波Sg震相在爆破记录图上无法识别,所以本研究弃用(图 2)。
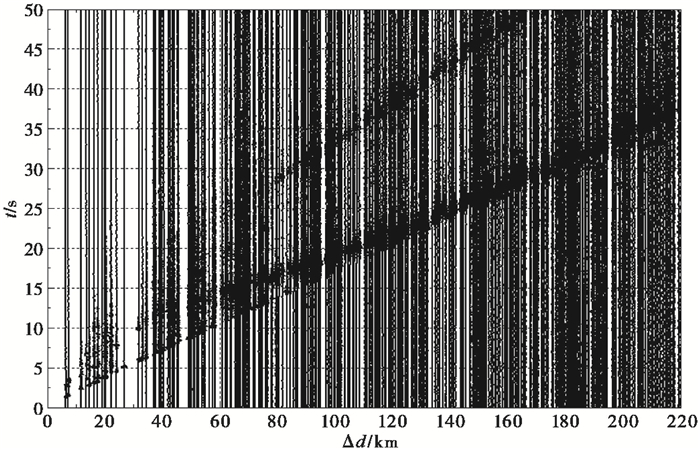
|
图 2 2010~2012年18次爆破记录 |
利用18次爆破记录作为研究资料,先进行爆破震相特征分析,一方面在华南模型基础上采用单纯型、Hyposat、Hypo2000及Locsat等4种定位方法进行定位偏差比较,得出最优定位方法。另一方面应用14次爆破记录反演福建一维两层速度模型,将研究得到的模型结果与华南模型进行比对,再用剩余的4次爆破记录对本研究模型进行验证(图 3)。
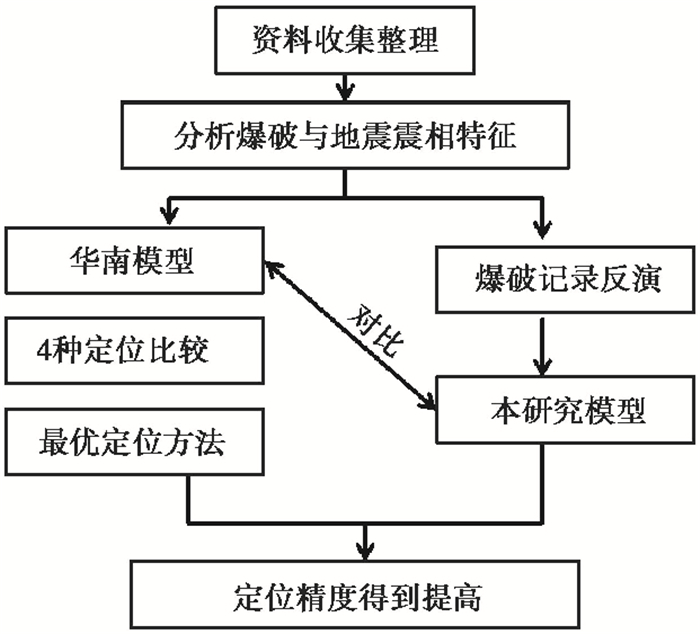
|
图 3 研究技术路线 |
福建区域开展的“福建及台湾海峡地壳深部构造探测实验”项目,产出了丰富的爆破记录数据,这为福建地震台网系统地识别爆破与地震波形特征创造了良好条件。本文对爆破实验震相波形与地震震相波形进行分析对比,区分爆破与天然地震的震相特征,得出了适用于福建地区的爆破识别判据,旨在提高地震分析人员的准确判断。
地震与爆破一样都是瞬间发生的,发生时都能释放出巨大的能量。然而,在发生机制上地震与爆破是有差异的,主要为:①爆破与天然地震的震源机制不同:爆破源是对称膨胀源,天然地震源则是非对称剪切源。②震源深度不同:爆破多位于近地表附近,一般深度为0~2km;而地震大多发生于地下5~30km处,有的更深达数百千米。
本文通过对18炮爆破记录的波形进行分析,得出爆破的特征如下:
(1) 爆破是膨胀源激发P波,导致了爆破的P波较强,而S波的激发能力较弱。而且在同一距离上,有时爆破的P波振幅能达到甚至超过S波的振幅。地震是非对称剪切源,激发P波能力较弱,而激发S波能力较强,一般来说,地震的P波振幅要小于S波的振幅(图 4)。
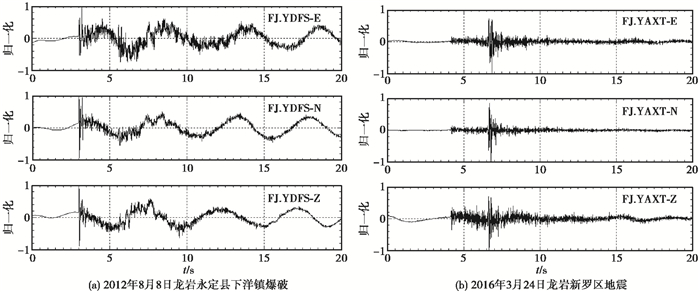
|
图 4 爆破与地震P波、S波震相对比 右上角为台站代码 |
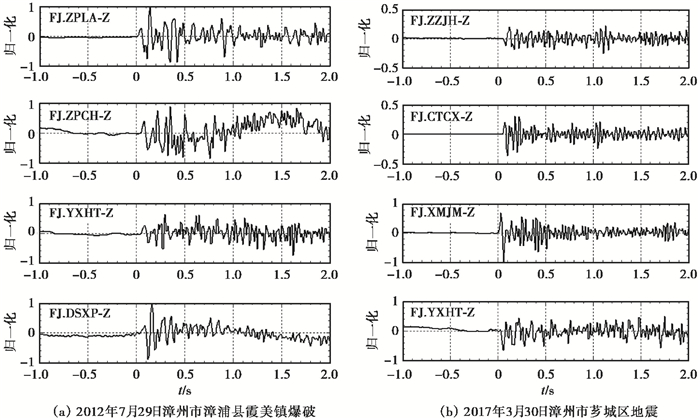
(2) 各向同性介质中,点源爆破的振幅与方位无关,且只有压缩初动,而地震的振幅和极性均会随方位变化(彼得·鲍曼,2006)。统计爆破和地震事件各台P波垂直向初动结果得出:爆破垂直向初动均向上;而地震垂直向初动有向上和向下,按象限分布(图 5)。
|
图 5 爆破与地震垂直向P波震相初动方向对比 左上角为台站代码 |
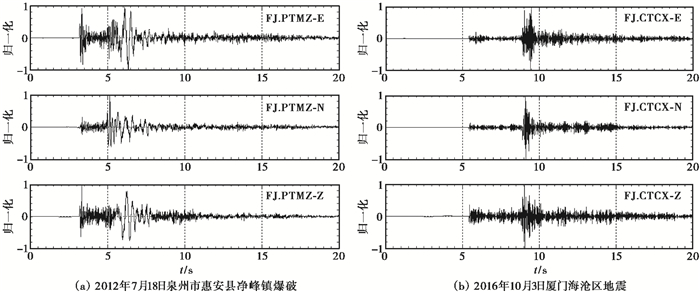
(3) 由于爆破的深度较浅,能激发出较清晰的面波,而且由于浅层对高频成分的吸收,传播一段距离后,波形显示很干净,毛刺较少。而地震的震源较深,激发面波的能力较弱,且毛刺较多(图 6)。
|
图 6 爆破与地震近台面波发育对比 右上角为台站代码 |
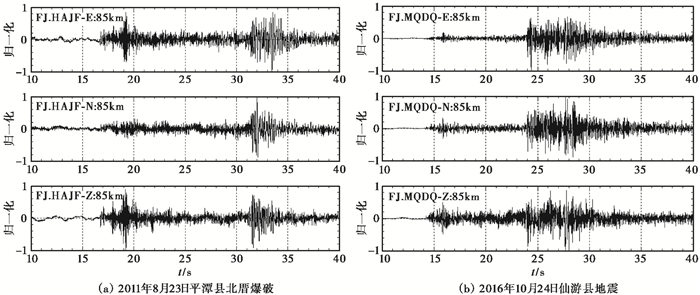
(4) 爆破在震中距70~90km或者70~110km处PmP波发育且其振幅较强并呈纺锥型,而地震在该震中距区间处PmP波发育且振幅较弱(图 7)。
|
图 7 爆破与地震反射波发育对比 左上角为台站代码及震中距 |
“十五”中国数字化地震观测网络项目以来,福建地震台网将广东智源科技有限公司开发的人机交互软件MSDP(Multiple Seismic Data Processing System)用于日常地震速报和地震编目。MSDP软件自带有6种定位程序,分别是单纯型法、遗传算法、单台定位法、Hyposat、Hypo2000、Locsat等。福建台网日常工作使用的有单纯型法、Hyposat、Hypo2000及Locsat等4种,它们有各自的适用范围(表 2)。这4种定位程序在使用中都配置了华南速度模型(范玉兰等,1988)。
| 表 2 4种定位方法的适用范围 |
本研究对18次爆破均用4种定位方法进行定位偏差对比分析(表 3、图 8)。由表 3、图 8可见,4种方法中,单纯型法定位平均偏差1.08,偏差中值0.923,为最高,离散度小,故属于一般;Hyposat方法平均偏差0.81,为最小,偏差中值0.831,离散度小,故属于较优;Hypo2000方法最大偏差5.50,为最大,离散度大,但是偏差中值0.645,为最低,故属于一般;Locsat定位方法平均偏差1.44,为最大,离散度大,偏差中值0.857,较大,故属于较差。
| 表 3 4种方法18炮定位偏差 |
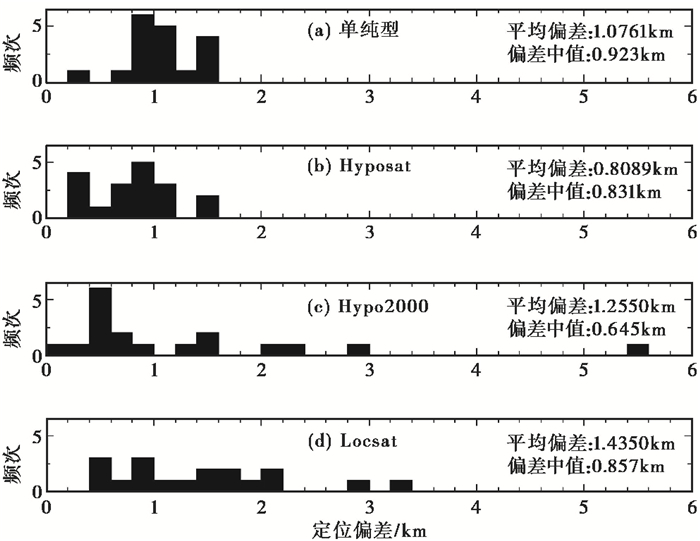
|
图 8 4种定位方法定位震中偏差比较 |
综合4种定位方法的统计分析可以看出,Locsat定位方法偏差大,离散度大,定位效果较差,故不将其纳入提高定位精度的方法中。Hypo2000虽然最大偏差大,离散度较大,但偏差中值较小,在特定的情况下可以考虑使用。单纯型定位离散度小,较为稳定,可以考虑作为本文提高定位精度使用。Hyposat定位偏差较小,离散度小,较为稳定,可以作为本文提高定位精度的首选方法。事实证明,在地震分析中,如果使用较为合适的定位方法来定位不同类型的地震,便可获得较为可靠的地震参数和震中位置,也能进一步提高地震分析的质量。
3 利用固定台观测资料反演福建一维速度模型 3.1 基础资料利用MSDP软件人工分析震相,共捡拾清晰Pn震相181个,震中距最大348.7km,最小136.4km;清晰PmP震相118个,震中距最大137.5km,最小56.1km(表 4)。本研究除利用SP31、SP14、SP24、SP42等4次爆破的Pn、PmP震相外,将其余14次爆破所有的Pn、PmP震相进行一维速度结构反演,这4次爆破用于反演结果的对比检验。用于一维速度结构反演Pn震相共计181个,PmP震相共计87个。
| 表 4 各次爆破捡拾震相数 |
以华南模型为基础,采用迭代搜索法,选取走时残差最小时对应的波速与厚度参数为最终结果。首先,假定地壳厚度与华南模型一致,分别为H1=21.4km,H2=11km,在此基础上利用正演的方法,分别确定各层波速。在得到波速后,重新利用正演方法确定H1、H2。
双层模型Pn走时方程可写为
| $ \mathit{t}\text{=}\frac{\text{ }\!\!\Delta\!\!\text{ }}{{{\mathit{v}}_{\text{3}}}}\text{+(2}{{\mathit{H}}_{\text{1}}}\text{-}\mathit{h}\text{)}\sqrt{\frac{\text{1}}{\mathit{v}_{1}^{2}}\text{-}\frac{\text{1}}{\mathit{v}_{3}^{2}}}\text{+2}{{\mathit{H}}_{\text{2}}}\sqrt{\frac{\text{1}}{\mathit{v}_{2}^{2}}\text{-}\frac{\text{1}}{\mathit{v}_{3}^{2}}} $ | (1) |
式中,v1、v2、v3分别为第1、2、3层的波速;Δ为震中距;h为震源深度。
双层模型PmP走时方程可写为
| $ \mathit{t}\text{=}\frac{\text{2}{{\mathit{H}}_{\text{1}}}}{{{\mathit{v}}_{\text{1}}}\sqrt{\text{1-}\mathit{v}_{1}^{2}{{\mathit{c}}^{\text{2}}}}}\text{+}\frac{\text{2}{{\mathit{H}}_{\text{2}}}}{{{\mathit{v}}_{\text{2}}}\sqrt{\text{1-}\mathit{v}_{2}^{2}{{\mathit{c}}^{\text{2}}}}} $ | (2) |
| $ \mathit{\Delta } \text{ =}\frac{\text{2}\mathit{c}{{\mathit{v}}_{\text{1}}}{{\mathit{H}}_{\text{1}}}}{\sqrt{\text{1-}\mathit{v}_{1}^{2}{{\mathit{c}}^{\text{2}}}}}\text{+}\frac{\text{2}\mathit{c}{{\mathit{v}}_{\text{2}}}{{\mathit{H}}_{\text{2}}}}{\sqrt{\text{1-}\mathit{v}_{2}^{2}{{\mathit{c}}^{\text{2}}}}} $ | (3) |
| $ \mathit{c}\text{=}\frac{\text{sin}{{\mathit{i}}_{\text{1}}}}{{{\mathit{v}}_{\text{1}}}}\text{=}\frac{\text{sin}{{\mathit{i}}_{\text{2}}}}{{{\mathit{v}}_{\text{2}}}} $ | (4) |
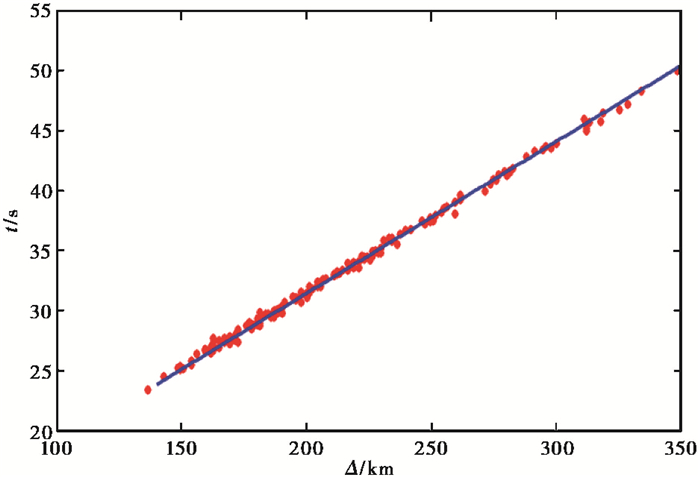
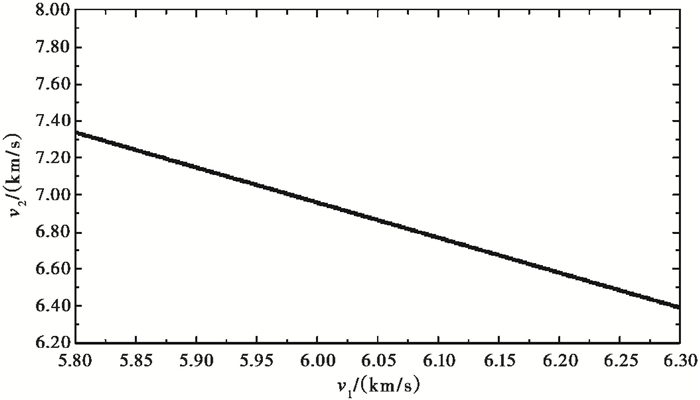
式中,c为射线参数。将H1=21.4km、H2=11km及Pn震相走时、震中距代入式(1),拟合可得第3层的波速v3=7.9119km/s,残差σ=0.29,拟合结果见图 9,在H1=21.4km、H2=11km时,可得到第1层速度v1和第2层速度v2间的关系(图 10),如第1层速度v1=6.1km/s,则第2层速度v2=7.0km/s。
|
图 9 莫霍面速度v3的拟合结果 |
|
图 10 震相走时差最小值对应的v1、v2间关系 |
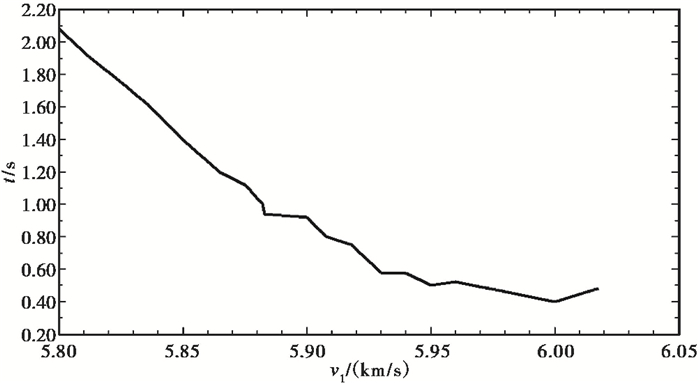
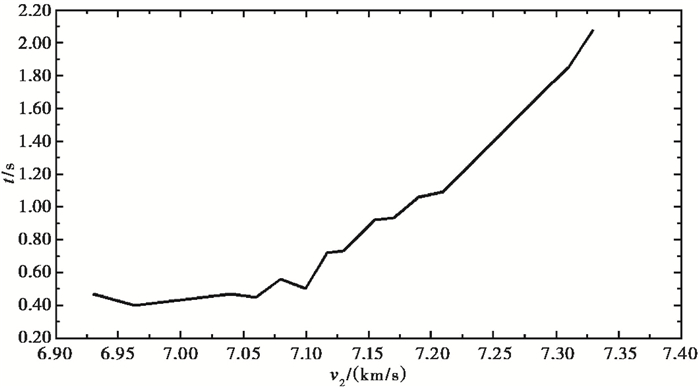
将图 10中得到的v1、v2直接代入双层模型PmP走时方程(式(2)、(3)、(4)),进一步寻找与震相走时差最小值所对应的v1、v2。拟定初值采用:H1=21.4km,H2=11km,经正演后得到:v1=6.00 km/s,v2=6.97km/s,其中,最小残差:0.39s,拟合结果见图 11、12。
|
图 11 第1层速度和震相走时差的拟合结果 |
|
图 12 第2层速度和震相走时差的拟合结果 |
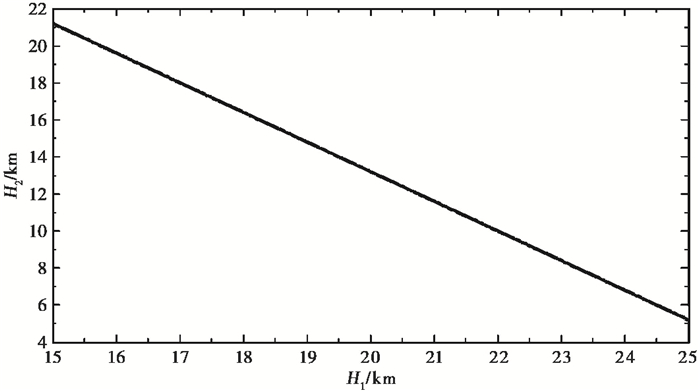
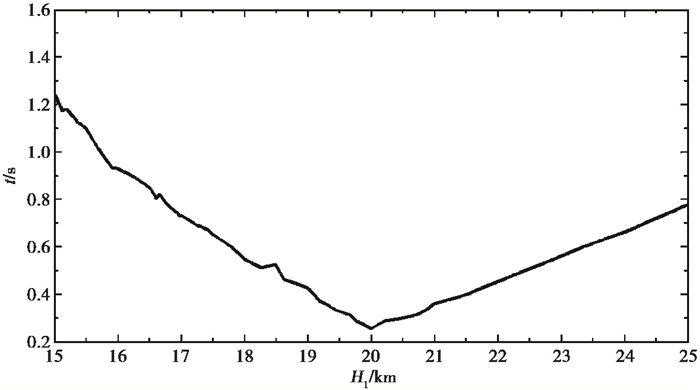
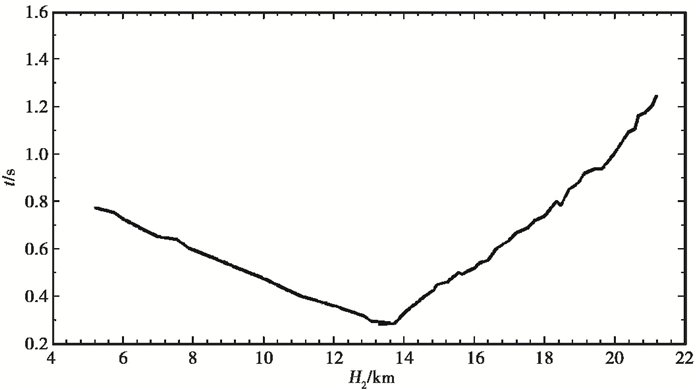
将得到的v1=6.00km/s、v2=6.97km/s直接带入式(1),即可获得第1层地壳厚度H1与第2层地壳厚度H2之间的关系(图 13),如取H1=15km,那么H2=21.5km代入式(2)、(3)、(4),搜索与震相走时差最小值所对应的H1、H2。令v1=6.00km/s,v2=6.97km/s,进一步正演可得H1=19.80km,H2=13.55km,最小残差=0.26s,拟合结果见图 14、15。
|
图 13 第1、2层地壳厚度间的关系 |
|
图 14 第1层地壳厚度与震相走时差的拟合结果 |
|
图 15 第2层地壳厚度与震相走时差的拟合结果 |
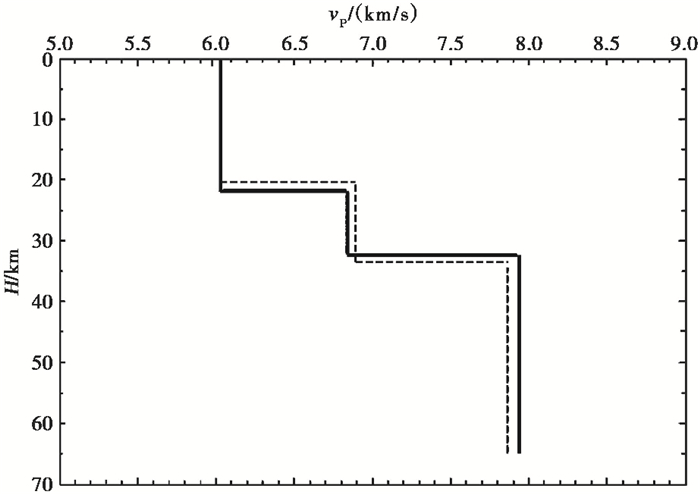
将本文研究结果进行汇总,并与华南模型进行对比(表 5、图 16)。由表 5及图 16可见,本研究结果上地壳厚度为19.8km,小于华南模型的21.4km,波速二者相当,下地壳厚度为13.55km,大于华南模型的11km,波速大于华南模型。
| 表 5 本文结果与华南模型对比 |
|
图 16 本研究模型与华南模型对比 虚线为本研究模型;实线为华南模型 |
将本研究结果采用到MSDP人机交互系统处理模块下,利用Hyposat方法对SP14、SP24、SP31、SP42等4次爆破进行定位,得到的定位偏差结果列于表 6。由表 6可见,采用本研究模型进行定位的结果比起华南模型偏差明显减少且4个爆破的偏差都小于1.00km,二者的平均定位偏差基本都能减少0.39km。
| 表 6 本研究模型与华南模型定位偏差比较 |
本文利用18次爆破实验的记录作为研究资料,首先进行了爆破震相特征的分析;然后,利用爆破实验的准确时间、地点及台网观测到的地震波走时信息,反演出福建一维两层速度模型;最后,在此基础上,利用华南模型及4种定位方法来检验地震定位方法的精度,进一步改善区域一维速度模型,以达到提高区域地震台网定位精度的目的。本研究主要取得如下结论。
(1) 通过对爆破震相与地震震相波形的对比分析,得到爆破震相特征:P波能量较强,S波的能量较弱;地震的初动按象限分布,爆破初动一般都向上且无象限分布;爆破面波较为发育。由此,得出较适用于识别本地区爆破的判据,以期有助于分析人员提高对地震类型的准确判断。
(2) 利用单纯型、Hyposat、Hypo2000及Locsat等4种定位方法对18次爆破记录进行重新定位分析。结果表明,Hyposat定位平均偏差最小,离散程度最小,较为稳定;Locsat偏差最大,精度最低。因此,在地震的定位分析工作中,采用Hyposat定位方法对爆破记录进行定位,可获得较为可靠的地震参数和震中位置。
(3) 利用14次爆破实验已获得的固定台网记录,反演福建一维速度模型,将该模型与华南模型进行对比得出:其上地壳厚度小于华南模型,下地壳厚度大于华南模型;上地壳速度与华南模型相当,下地壳速度大于华南模型。利用本研究反演结果对其他4次爆破进行重新定位,定位精度都明显提高。
| 彼得·鲍曼, 2006, 新地震观测实践手册, 462~470, 北京: 地震出版社. |
| 陈棋福, 张跃勤, 周静, 等. 2001, 数字观测时代的全球三维结构与地震定位研究. 地震, 21(2): 29–40. |
| 陈祥熊, 林树, 李祖宁, 等. 2005, 福建-台湾地区一维地壳速度结构的初始模型. 地震, 25(2): 61–68. |
| 范玉兰, 林纪曾, 胡瑞贺, 等. 1990, 华南地区近震走时表的研制. 华南地震, 10(2): 1–16. |
| 廖其林, 王振明, 王屏路, 等. 1988, 福州-泉州-汕头地区地壳的爆炸地震研究. 地球物理学报, 31(3): 270–280. |
| 孙安辉, 陈棋福, 陈颙, 等. 2011, 天山东北部地震的重新定位和一维地壳速度模型的改善. 中国地震, 27(3): 235–247. |
| 张先康, 杨玉春, 赵平, 等. 1994, 唐山滦县震区的三维地震投射研究——中、上地壳速度层析成像. 地球物理学报, 37(6): 759–766. |
| 赵仲和. 1983, 多重模型地震定位程序及其在北京台网的应用. 地震学报, 5(2): 242–254. |
| Shearer. 1999, Introduction to seismology. Cambridge: Cambridge Univeisity Press |
| Bondár I, Myers S C, Engdahl E R. 2004, Epicentre accuracy based on seismic network criteria. Geophys J Int, 156(3): 483–496. DOI:10.1111/gji.2004.156.issue-3. |
 2018, Vol. 34
2018, Vol. 34

