随着观测技术的发展和地震台站的密集化,地震学家对天然地震波的传播规律以及地球内部结构的研究也越来越多。地震通常被认为是由地下应力的积累和释放所造成的,因此,地下介质应力状态及其变化是地震发生的关键因素(陈蒙,2015),而介质应力状态的变化则会引起地震波波速的变化(Birch,1960、1961;Scholz,1968;Nur et al,1969)。迄今为止,地震波是所知的唯一能够穿透地球内部的振动(陈颙等,2005),因此,通过测量地震前后的波速变化,认识地下介质应力状态的演化,对地震预测研究具有重要意义。
目前,国内外有关学者分别利用重复地震、噪声和人工震源等研究地下介质的动态变化(Schaff et al,2004;Brenguier et al,2008;Siliver et al,2007;Niu et al,2008;陈颙等,2006、2007a;林建民等,2006;Wang et al,2008;王伟涛等,2009)。但重复地震发生的时间和地点不可控制,加之天然地震定位精度有限,因此,无法进行长期的动态监测;而噪声源能量较弱,需要长时间叠加才能获得可靠的测量结果。上述因素都限制了利用天然源测量地下介质时空变化的精度及分辨率(王宝善等,2011)。而人工震源具有震源位置已知、激发时间可控、观测系统分布灵活方便、可以进行密集观测等优点,在区域尺度研究中有望弥补天然源在精度上的不足(杨微等,2013)。利用人工震源进行主动地震探测已成为高精度探测地下介质波速变化的方法之一,而利用大容量气枪震源作为主动震源对区域尺度进行地下介质探测和监测则更具有高度的可重复性、能量强、探测距离远、绿色环保等优势。
通常,地下介质的应力变化所引起的地震波波速变化很小,故需要不断提高地震波波速测量的精度。测量波速的几种常用方法中,干涉法是测量波速精度最高的方法,而基于互相关时延检测的干涉法已被广泛用于地震波波速测量中,并取得一些显著的进展。Niu等(2008)在美国San Andreas断层上的SAFOD井内采用主动源的方法,利用互相关延迟检测技术,在井深1m处成功观测到了由大气压和固体潮引起的波速变化,同时还观测到在距井3km以外的1次M3.0地震震前,波速明显地增加(8%)。Wang等(2008)在云南昆明进行的主动源探测中,利用基于互相关时延检测技术的尾波干涉方法,也观测到了介质波速变化与大气压变化间有良好的相关性。
地震波走时与波速间密切相关,精确测量走时变化可获取地震孕育过程中的有关信息。本文利用祁连山主动源2015年7月~2016年5月的气枪激发数据,选取2016年青海门源6.4级地震震中附近以及距门源地震震中较远的相关台站接收到的气枪激发信号,采用互相关时延检测技术,对青海门源6.4级地震前后的走时变化进行了测量,并对地震前后波速的变化进行了初步分析。
1 资料选取祁连山主动源激发系统自2015年7月运行以来,为尽可能减少噪声对激发信号的干扰,选择每周一晚至周二凌晨进行连续激发,每次激发间隔时间约为12min,每周可以获得40~50次的激发数据。根据秦满忠等(2017)的研究,祁连山主动源每周激发数据经过叠加之后可被200km以外的台站观测到。其中,2015年9月30日~11月6日进行了24h的连续激发实验。截至2016年7月1日,累计有效激发约6400次,数据基本连续,为后续的研究提供了可靠的数据保障。
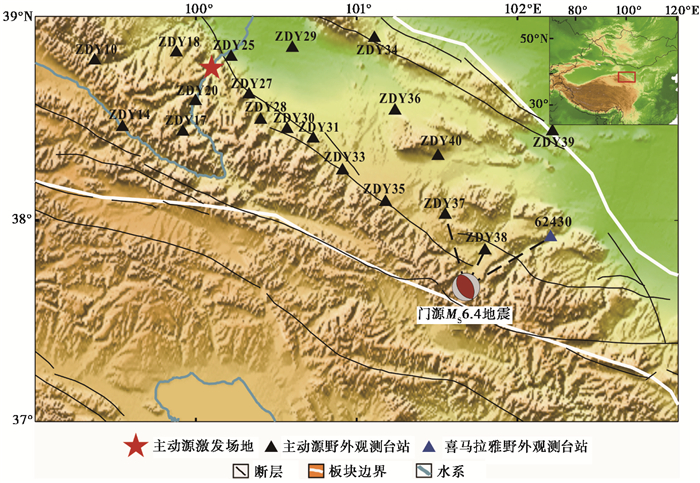
2016年1月21日,青海门源发生了6.4级地震,此次地震震中恰好位于祁连山主动源监测区域的边缘,距祁连山主动源激发场地178km,最近的主动源台站(ZDY38号台)距震中25km。白超英(1999)研究认为,1个6级地震的震源区范围一般为数十千米,为此选取震源区内ZDY38、ZDY37、喜马拉雅二期流动62430台以及距地震震中较远(距气枪震源较近)的台站ZDY28、ZDY30、ZDY31进行处理、对比分析(图 1、2)。
|
图 1 选取台站、主动源位置及门源地震震源区位置 |
|
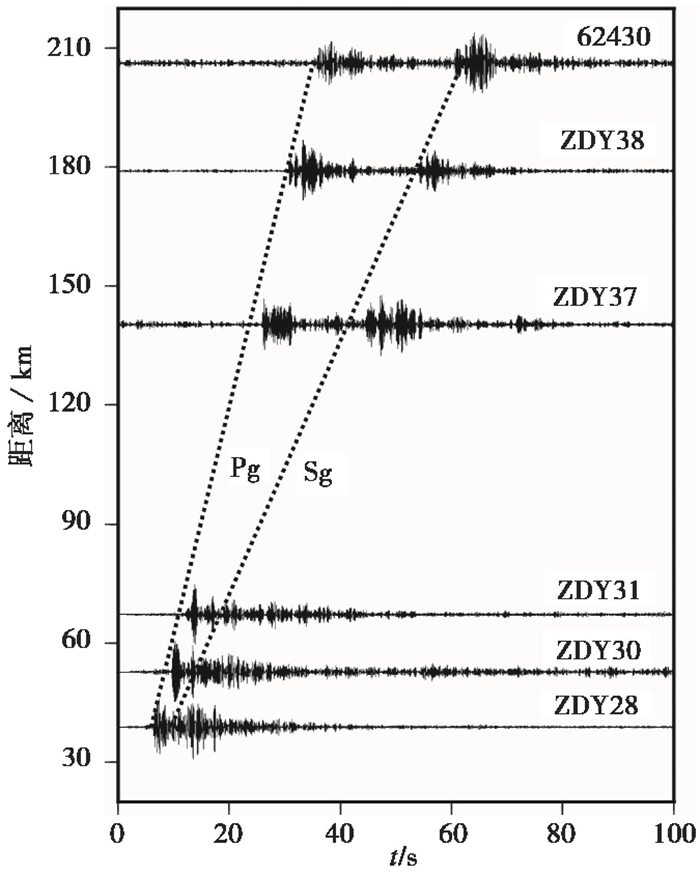
图 2 所选台站走时剖面 线性叠加50次;带通滤波3~7Hz |
移动窗互相关是互相关延时检测中最常用的方法,其原理是对比2列高度相似的波形,由参考波形干涉另一列波形,给定1个时间窗,通过移动该时间窗求取互相关函数最大值,以获得走时延迟进而求得波速变化。定义记录点的初始波形为u(t),扰动后的波形为
| $ \mathit{R}\text{(}{{\mathit{t}}_{\text{s}}}\text{)=}\frac{\int_{\mathit{t-}\frac{\mathit{T}}{\text{2}}}^{\mathit{t}\text{+}\frac{\mathit{T}}{\text{2}}}{\mathit{u}\left({\mathit{{t}'}} \right)\mathit{\tilde{u}}\text{(}\mathit{{t}'}\text{+}{{\mathit{t}}_{\text{s}}}\text{)d}\mathit{{t}'}}}{\sqrt{\int_{\mathit{t-}\frac{\mathit{T}}{\text{2}}}^{\mathit{t}\text{+}\frac{\mathit{T}}{\text{2}}}{{{\mathit{u}}^{\text{2}}}\left({\mathit{{t}'}} \right)\text{d}\mathit{{t}'}}\int_{\mathit{t-}\frac{\mathit{T}}{\text{2}}}^{\mathit{t}\text{+}\frac{\mathit{T}}{\text{2}}}{{{{\mathit{\tilde{u}}}}^{\text{2}}}\left({\mathit{{t}'}} \right)\text{d}\mathit{{t}'}}}} $ | (1) |
其中,ts为时间变量;t为时间窗T的中心位置,当ts=t、互相关函数取最大值时,则称t为时间窗T内的走时延迟。
当波速为v的介质发生dv的到时变化时,其走时延迟dt与流逝时间t间有如下关系
| $ \frac{\text{d}\mathit{v}}{\mathit{v}}\text{=-}\frac{\text{d}\mathit{t}}{\mathit{t}} $ | (2) |
假设介质中速度变化均匀,如果介质波速降低(或增大),则走时延迟将随流逝时间而线性增加(或减小)(Snieder,2006),线性拟合走时延迟与流逝时间之间所得直线斜率的负数即为介质波速的相对变化。
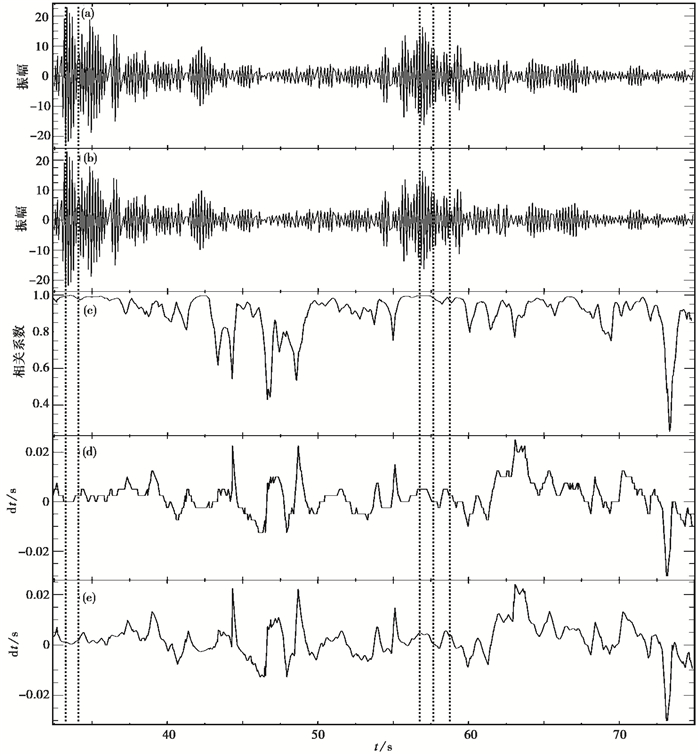
2.2 数据处理方法 2.2.1 利用互相关技术获取激发时刻对2015年7月~2016年5月间的数据进行筛选,手动去除信噪比较差和记录错误的个别波形。由于波形存在一些非介质变化所引起的信号影响(如直流量、趋势项等),需要同时对数据进行去均值、去趋势等处理。然后,利用互相关技术获取激发时刻,以祁连山主动源发射场地旁边的ZDY22号台(距气枪激发源约80m)为参考台,截取某个晚上参考台接收到的激发信号为原始模板,分别对参考台每天的数据进行互相关,得到激发时刻(图 3)。
|
图 3 互相关时延检测示意 (a)参考模板(ZDY38);(b)格林函数(ZDY38,2015-07-09);(c)相关系数;(d)插值前走时延迟;(e)插值后走时延迟。竖直虚线表示所选取有效信号的时间窗 |
以激发时刻为零时,对每个台的数据截取激发时刻后200s的数据,采样率为100Hz。为了消除触发误差、水位等因素对气枪震源的影响,将每个台截取的数据分别对参考台接收到的激发信号进行反褶积。由于单次激发的气枪信号会湮没在噪声中,因此,需要通过叠加来提高信噪比,以获得有效的气枪激发信号,故将所选台站的所有数据进行叠加作为参考模板。对震源区内台站每2周的数据进行叠加,可得到时间间隔为14天的格林函数;对于距主动源发射场较近的台站,则可得到时间间隔为7天的格林函数。在2015年10~11月不间断激发实验期间,数据叠加的时间间隔为3天。最后,带通滤波至3~7Hz,以减少噪声的影响。
2.2.3 互相关时延检测通过对每2周得到的格林函数与相应台站的参考模板进行移动窗互相关,在得到最大相关系数时可获取走时延迟。原始数据的采样率为100Hz,这意味着获得的最小走时延迟为0.01s。但有时相关函数的最高峰值不一定在采样点上,而是偏离采样点一定的距离。为此,我们选择余弦插值的方法来恢复相关函数的峰值位置,从而得到亚采样点的时间精度(王伟涛等,2009)。图 3(d)、3(e)分别为插值前、后走时延迟图。由图 3(d)、3(e)可见,使用余弦插值后可得到更高精度的走时延迟。根据式(2),对走时延迟求取平均值与方差,即得到相对平均波速的相对变化量与计算误差。
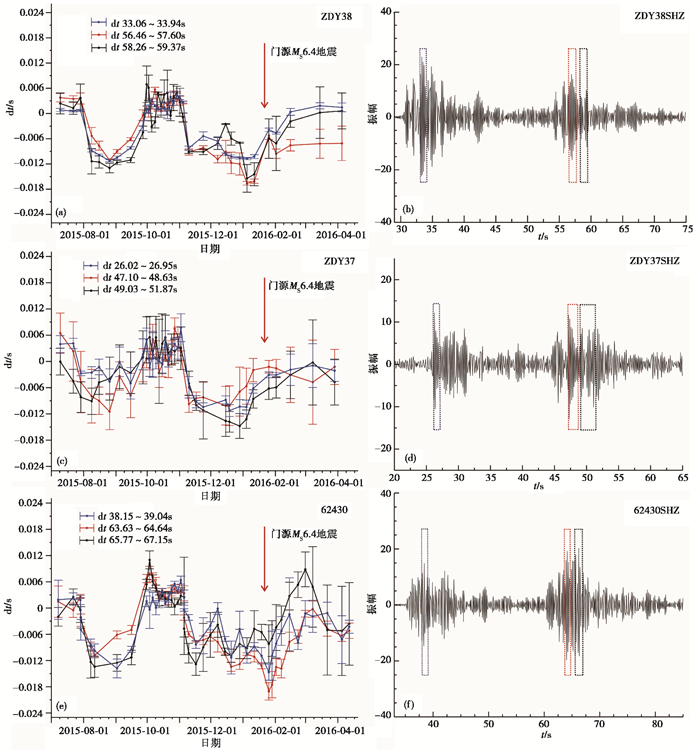
3 地震前后走时变化测量结果ZDY38台站距门源地震震中25km,选取P波最大振幅33.06~33.94s、S波最大振幅56.46~57.60s、S波58.26~59.37s等3段时间窗,通过互相关时延检测计算其走时变化(图 4)。由图 4可见,2015年8月初至9月底走时变化出现持续近2个月的低值异常,随后又逐渐回升。而在2015年11月4日,走时变化又出现第2次下降,幅度最大达-18ms,低值异常持续至2016年1月21日门源6.4级地震发生,震后走时变化逐渐回升,至2016年3月25日,走时变化逐渐恢复正常。
|
图 4 震源区内所选台站的走时变化及时间窗选取 |
对于距门源地震震中41km的ZDY37台站,计算其P波最大振幅26.02~26.95s、S波最大振幅47.10~48.63s、S波49.03~51.87s等3组时间窗内的走时变化(图 4)。由图 4可见,ZDY37台站与ZDY38台站走时变化趋势较为一致,2015年8月初至9月底出现第1次低值异常,之后恢复正常。2015年11月4日走时变化再次出现下降,最低值出现在2016年12月28日,走时变化幅度最大幅度为-16ms,随后走时变化开始上升,在上升过程中发生了门源6.4级地震,至2016年3月14日恢复正常。
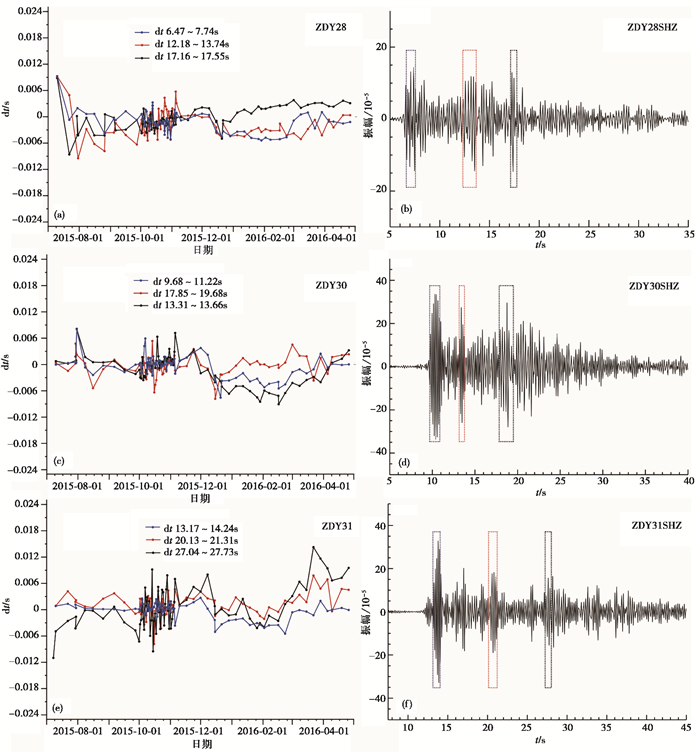
对于距门源地震震中53.8km的62430台站,计算其P波最大振幅前后38.15~39.04s、S波最大振幅前后63.63~64.64s、S波65.77~67.15s等3组时间窗内的走时变化(图 5)。由图 5可见,2015年7月28日走时变化出现第1次低值,并持续至9月底,2015年9月30日恢复正常。而在2015年11月4日,走时变化第2次出现低值,这与ZDY38、ZDY37两个台有所不同,62430台的走时变化在门源地震震前一直持续低值,最大变化幅度达-13ms,门源地震发生后,走时变化于2015年1月25日出现最低值,随后走时变化开始逐渐上升,直到2015年3月7日恢复正常。
|
图 5 远离震中所选台站的走时变化及时间窗选取 |
杨微等(2010)研究绵竹MS5.6地震前后波速的变化后认为,地震发生前,断裂带附近区域应力逐渐积累,波速增加,而地震发生后应力的释放导致波速相对下降。2016年门源6.4级地震前,远离震中的ZDY28、ZDY30、ZDY31等台站走时变化趋势较小,没有出现明显的低值异常过程(图 5)。地震前约6个月,震中附近的ZDY38、ZDY37、62430等台站的相对走时出现下降变化(走时减少),至震前约3个月低值异常恢复,之后再次出现走时下降变化,这可能与孕震区内地下介质应力持续积累而导致穿过该区域的地震波速度增加有关。
4 结论与讨论 4.1 误差分析走时延迟的误差下限στ可由Cramer-Rao Lower Bound法则来计算(刘自凤等,2015),即
| $ {{\mathit{\sigma }}_{\mathit{\tau }}}\ge \sqrt{\frac{\text{3}}{\text{2}\mathit{f}_{0}^{3}{{ \pi }^{\text{2}}}\mathit{T}\text{(}{{\mathit{B}}^{\text{3}}}\text{+12}\mathit{B}\text{)}}\left[ \frac{\text{1}}{{{\mathit{\rho }}^{\text{2}}}}{{\left(\text{1+}\frac{\text{1}}{\text{SNR } ~ } \right)}^{\text{2}}}\text{-1} \right]} $ | (3) |
其中,f0为信号主频;T为时间窗长度;B为信号的频宽比;ρ为波形的相关系数;SNR为信噪比。由式(3)可见,波形的相似度、信噪比和信号的频宽与主频之比等是影响走时延迟测量精度的主要因素(张金川等,2014)。
祁连山主动源的主频基本为5Hz,信号的能量主要集中在4.5~6.5Hz,故选取f0≈5Hz,B≈0.4,在进行互相关时延检测时,选取窗长T=0.4s,选取ρ≈1,SNR≈15,则式(3)可简化为
| $ {{\mathit{\sigma }}_{\mathit{\tau }}}\ge \frac{\text{1}}{\text{2 } \pi {{\mathit{f}}_{\text{0}}}\cdot \text{SNR}}\sqrt{\frac{\text{1}}{{{\mathit{f}}_{\text{0}}}\mathit{TB}}} $ | (4) |
式(4)可得,走时延迟的理论误差下限约为2.37×10-4s。而在进行互相关时求得走时延迟的均方差约为6.15×10-4s,可见实测误差与理论误差非常接近,但比ZDY38、ZDY37、62430等台观测到的走时变化值小1个数量级。
除计算误差以外,测量的精度还受观测系统和环境因素等的影响(杨微等,2010)。祁连山主动源台站采用GPS连续授时方式,其授时精度为10-7μs,比计算得到的直达S波走时变化值的精度高3个数量级。固体潮和气压的影响是一个复杂的问题,数据的叠加对这些影响有一定的消弱作用,故叠加处理后的波形数据受固体潮和气压的影响可能不大。
4.2 结论与讨论本文利用祁连山主动源2015年7月~2016年5月的气枪激发数据,选取2016年青海门源6.4级地震震中附近、距震中较远的相关台站接收到的气枪激发信号,采用互相关时延检测技术对青海门源6.4级地震前后的走时变化进行了测量,结果表明,远离震中的ZDY28、ZDY30、ZDY31等台站的走时变化趋势较小,没有出现明显的低值异常过程;在地震前约6个月,震中附近3个台站的相对走时出现下降变化(走时减少),至震前约3个月低值异常恢复,之后再次出现走时下降变化,门源6.4级地震发生于走时变化恢复过程中。S波走时变化最大下降幅度达-18ms,震后走时变化逐渐恢复正常,且3个台站的变化趋势较为一致。
地震发生前,断裂带附近区域应力逐渐积累,波速增加,而地震发生后应力释放而导致波速相对下降(杨微等,2010)。走时缩短意味着速度增加,这可能与区域应力积累间存在一定的关系。远离震中的ZDY28、ZDY30、ZDY31等台站走时变化一直较小,震中附近ZDY38、ZDY37、62430等3个台站的震前走时变化持续低值,可能与2016年门源6.4级地震孕震过程中由于应力的积累而导致的穿过该区域的地震波速度的增加有关。ZDY38台站震前S波平均波速相对变化为0.38%,ZDY37号台站为0.27%,62430台站为0.15%,由此可见,距昌马-俄博断裂和门源6.4级地震震中最近的ZDY38台站波速相对变化最明显。
祁连山主动源气枪激发观测数据的处理和应用研究才刚刚起步,本文得到的结果较为初步,但研究结果将有助于观测数据结果的快速产出和地震相关波速变化信息的分析,以期尽快为地方防震减灾提供服务。
致谢: 互相关时延计算程序由中国地震局地球物理研究所地震观测与地球物理成像重点实验室王宝善研究员提供,在此表示衷心感谢。| 白超英. 1999, 中强地震密集区与未来强震三要素关系的研究. 西北地震学报, 21(1): 48–54. |
| 陈蒙. 2015, 利用水库大容量非调制气枪阵列进行区域尺度地下结构探测和监测. 国际地震动态(3): 41–42. |
| 陈颙, 王宝善, 葛洪魁, 等. 2007a, 建立地震发射台的建议. 地球科学进展, 22(5): 441–446. |
| 陈颙, 周华伟, 葛洪魁. 2006, 华北地震台阵探测计划. 大地测量与地球动力学, 25(4): 1–5. |
| 陈颙, 朱日祥. 2005, 设立"地下明灯研究计划"的建议. 地球科学进展, 20(5): 485–489. |
| 林建民, 王宝善, 葛洪魁, 等. 2006, 重复地震及其在人工探测中的潜在应用. 中国地震, 22(1): 1–9. |
| 刘自凤, 苏有锦, 王宝善, 等. 2015, 宾川主动源地震波走时变化分析方法研究. 地震研究, 38(4): 591–597. |
| 秦满忠, 刘旭宙, 邹锐, 等. 2017, 甘肃祁连山大容量气枪主动源最大探测范围. 地震工程学报, 39(6): 1070–1075. |
| 王宝善, 王伟涛, 葛洪魁, 等. 2011, 人工震源地下介质变化动态监测. 地球科学进展, 26(3): 249–256. |
| 王伟涛, 王宝善, 葛洪魁, 等. 2009, 利用主动震源检测汶川地震余震引起的浅层波速变化. 中国地震, 25(3): 223–233. |
| 杨微, 葛洪魁, 王宝善, 等. 2010, 由精密控制人工震源观测到的绵竹5.6级地震前后波速变化. 地球物理学报, 53(5): 1149–1157. |
| 杨微, 王宝善, 葛洪魁, 等. 2013, 大容量气枪震源主动探测技术系统及实验研究. 中国地震, 29(4): 399–410. |
| 张金川, 王勤彩, 薛兵, 等. 2014, 用尾波干涉法监测介质波速变化研究进展. 地震, 34(3): 62–73. |
| Birth F. 1960, The velocity of compressional waes in rocks to 10 kilobars, part 1. J Geophys Res, 65: 1083–1102. DOI:10.1029/JZ065i004p01083. |
| Birth F. 1961, The velocity of compressional waes in rocks to 10 kilobars, part 2. J Geophys Res, 66: 2199–2224. DOI:10.1029/JZ066i007p02199. |
| Brenguier F, Campillo M, Hadziioannou C, et al. 2008, Postseismic relaxation along the San Andreas Fault at Parkfield from continuous seismological observations. Science, 321: 1478–1481. DOI:10.1126/science.1160943. |
| Niu F L, Silver P G, Daley T M, et al. 2008, Preseismic velocity changes observed from active source monitoring at the Parkfield SAFOD drill site. nature, 454: 204–208. DOI:10.1038/nature07111. |
| Nur A, Simmons G. 1969, The effect of saturation on velocity in low porosity rocks. Earth Planet Sci Lett, 7(2): 183–193. DOI:10.1016/0012-821X(69)90035-1. |
| Schaff D P, Beroza G C. 2004, Coseismic and postseismic velocity changes measured by repeating earthquakes. J Geophys Res, 109: B10302. DOI:10.1029/2004JB003011. |
| Scholz C H. 1968, Microfracturing and the inelastic defomation of rock in compression. J Geophys Res, 73: 1417–1432. DOI:10.1029/JB073i004p01417. |
| Silver P G, Daley T M, Niu F L, et al. 2007, Active source monitoring of cross-well seismic travel time for stress-induced changes. Bull Seismol Soc Am, 97(1B): 281–293. DOI:10.1785/0120060120. |
| Snieder R. 2006, The theory of coda wave interferometry. Pure Appl Geophys, 163(2/3): 455–473. |
| Wang B S, Zhu P, Chen Y, et al. 2008, Continuous subsurface velocity measurement with coda wave interferometry. J Geophys Res, 113(B12). DOI:10.1029/2007JB005023. |
 2018, Vol. 34
2018, Vol. 34



