基于多震相联合反演江苏地区一维速度模型研究
李细兵, 赵启光, 朱峰, 洪海春, 王恒知
中国地震  2018, Vol. 34 2018, Vol. 34 Issue (2): 312-321 Issue (2): 312-321
|
传统的利用天然地震走时获取一维速度模型主要有Herglotz-Wiechert方法、线性拟合方法、τ(p)方法等(Shearer,2009),这些方法使用的前提是震源位置较为准确,这是因为其主要是利用台站与震源之间的走时资料来反演一维速度结构。除了单独反演速度结构外,现在有很多种方法能同时反演速度结构和震源参数,其中,使用较为广泛的是Kissling等(1994)提出的最小一维速度模型方法,该方法已广泛应用于国内外许多地区的速度模型反演中,并取得了丰富的研究结果(于湘伟等,2003;赵旭等,2007;李铂等,2012;王小娜等,2015;柯乃琛等,2016)。此外,田玥等(2006)采用拟牛顿法与信赖域法结合的方法对北京地区地震震源和速度模型进行联合反演,取得了较好的效果。但是,同时反演震源位置和速度结构需要在地震的定位误差和速度的扰动足够小的条件下,才能使得包括震源和速度在内的未知数联合方程是线性的;否则,定位的误差将会直接影响速度结构的准确性,进而造成速度结构的不准确,因此,这是进行震源和速度同时联合反演的首要条件。实际上,由于地球介质存在横向非均一性,大多数一维速度模型的构建过程都是各层介质速度平均化的过程。
准确的三维速度模型是诸如大尺度构造应力场、地球动力学等研究的基础性资料,而较好的一维速度模型不仅可以提高地震定位的精度,还可以为各种三维地震成像结构提供可靠的初始模型。地震定位时很多地区的一维速度模型是建立在深反射地震剖面基础上的,通过深反射地震剖面能得到较为准确的二维地壳速度结构和莫霍面深度信息,杨文采等(1999b)对穿过江苏北部的郯城-涟水综合地球物理剖面进行了深地震反射和大地电磁调查,但并未给出该反射剖面的具体深度和速度特征;在另一条从诸城到日照方向的剖面给出了地壳到地幔的速度结构(杨文采等,1999a),并将各深度的速度结构与岩性相对应起来,该速度结构可为江苏北部地区的速度结构提供一种参考。王有学等(2004)利用布置在苏北的中国大陆科学钻探井的2条折射/反射地震剖面研究认为,该钻探场址区的地壳速度结构可分为上地壳、中地壳、下地壳3层,各层厚度均为10km左右,整个地壳的平均速度为6.3km/s。从符离集(安徽)到奉贤(上海)的HQ-13宽角反射地震剖面穿越整个江苏中部地区,该速度结构在江苏中南部具有一定的代表性,白志明等(2006)对该剖面进行了新的处理和解释,揭示了该剖面上地壳深度为10~13km,速度为5.9~6.0km/s;中地壳深度为21~25km,速度为6.3~6.4km/s;下地壳分为2层,上层深度为25~29km,速度为6.6~7.0km/s,下层深度为30~36km,速度为6.9~7.0km/s。在层析成像方面,很多研究者使用的初始一维速度模型参考了周边区域的深地震反射剖面结果(徐佩芬等,2000;徐纪人等,2003;黄耘等,2011)。对于江苏地区,黄耘等(2011)综合各种深地震反射资料结果,将该区域的地壳及上地幔分为7层速度模型,以此作为地震定位和区域三维速度反演的初始模型。尽管建立在深地震反射剖面基础上的初始模型有较好的约束能力,具有一定的代表性,但往往成像覆盖的地区范围远远超过深地震反射所能覆盖的区域,因此,存在一定的不足。如果能采用具有较好定位水平的地震数据本身构建出一维P波速度模型,由于地震射线覆盖整个研究区,则能有效代表研究区的平均速度结构。在地震定位方面,目前江苏台网常规地震定位使用的一维速度模型主要是全球iasp91模型。这种2层模型具有分层简单、能追踪到多种震相等特点。但是,该模型是建立在整个全球尺度基础上的,对于具体地区的地震定位水平还有较大的提升空间。
鉴于江苏地震台网记录的震相资料中含有大量的续至Pg波震相,这些震相在传统的走时反演速度结构中很少利用,本文同时利用初至波、续至波震相,采用Pg、Pn波震相走时联合反演江苏地区一维P波速度模型,以期为后续江苏地区三维速度结构以及地震定位研究提供较可靠的一维速度模型。
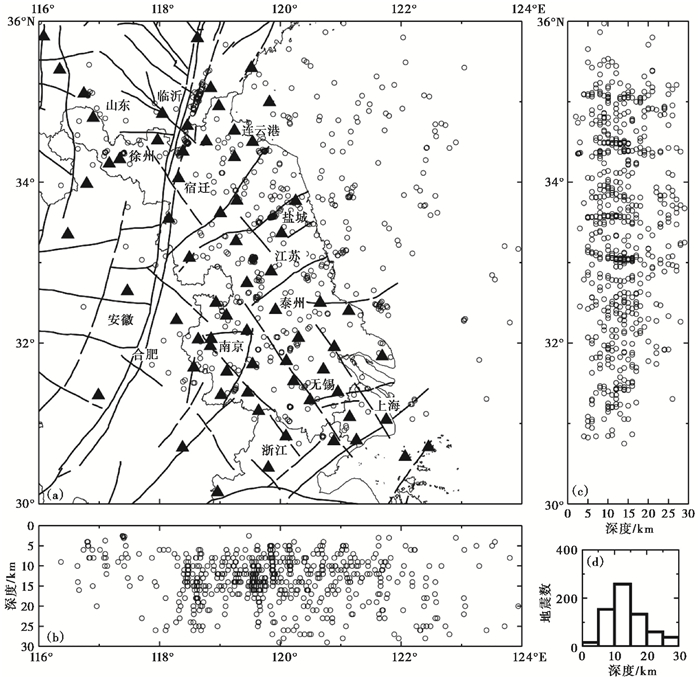
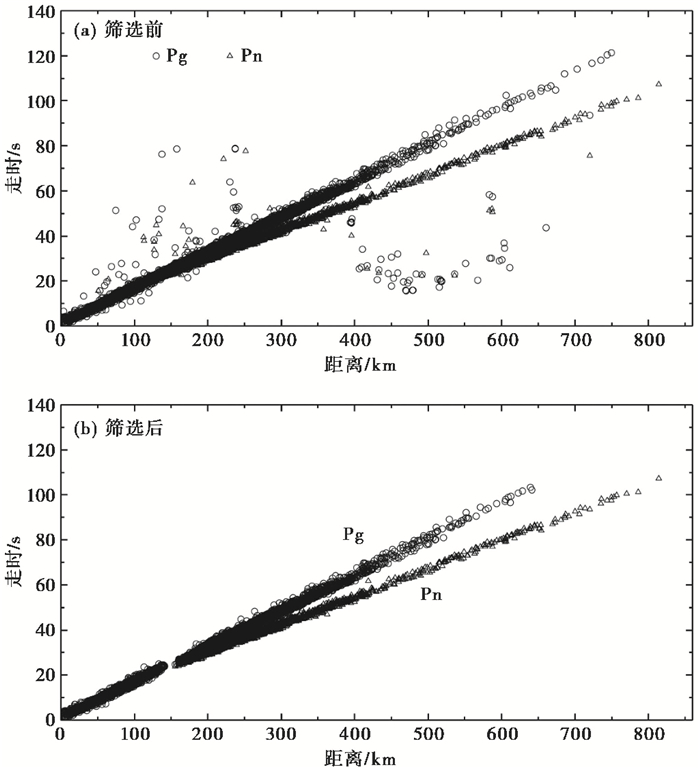
1 数据与方法本文收集了2008~2016年间江苏地震台网记录的地震P波震相数据,其包含有Pn、Pg震相走时数据,所有地震都给出了震源深度,同时具有相对较好的定位精度。为了进一步提高数据的精度,同时考虑到震源向下沿莫霍面折射滑行产生Pn波的特性,对数据进行了筛选,设置震源深度小于30km,每个地震的P波记录不少于10个,这可使得震源具有相对较高的定位精度,从而提高数据走时的精度(图 1)。经过筛选后,共有76个台站、661个地震,总的走时数据约14000条,其中,来自地壳的Pg震相走时数据约10000条,其余为Pn震相走时数据。这些地震的震源深度小于15km的占总数70%,说明江苏地区绝大多数地震发生在中上地壳以内。由图 1可见,江苏境内绝大部分地区都有地震记录,在附近海域也有大量的地震分布;沿郯庐断裂带山东境内有较多的地震分布,而在江苏境内的宿迁段地震数量明显偏少,远不如江苏其他地区,在其右侧的徐州和其左侧的盐城地区都有较多的地震发生,但震级都较小。从筛选后的时距曲线(图 2(a))可见,台网记录中含有大量来自地壳的续至Pg波,包含初至波和续至波在内的地壳Pg波与上地幔顶部Pn波震相区分较为明显,当震中距大于300km时,续至波与Pn波逐渐分离开来,但是由于走时拾取等原因,时距曲线具有十分明显的走时误差,我们将采用新方法对其进行处理。
|
图 1 研究区2008~2016年地震空间分布与震源深度统计 黑色线段表示断裂;黑色实心三角形表示台站;黑色空心圆表示地震 |
|
图 2 不同震相数据筛选前后对比 |
本文采用Xu等(2010)提出的联合Pg和Pn方法来反演江苏地区地壳及上地幔一维P波速度结构。该方法对地壳Pg波震相和上地幔顶部Pn波震相走时分别采用不同方法计算,对前者采用直接利用球面坐标系下伪弯曲射线追踪方法(Koketsu et al,1998),对后者利用Pn波震相的折射波性质分段计算走时。
对于地壳Pg波射线,从第j个震源到第k个台站的走时残差表示为
| $ {{\mathit{r}}_{\mathit{jk}}}\text{=}\mathit{t}_{\mathit{jk}}^{\text{obs}}\text{-}\mathit{t}_{\mathit{jk}}^{\text{pre}}\text{=}\sum\nolimits_{\mathit{r}=1}^{\mathit{n}\text{1}}{\left(-\frac{\text{d}\mathit{l}}{\mathit{v}} \right)\left(\frac{\Delta \mathit{v}}{\mathit{v}} \right)} $ | (1) |
其中,tjkobs为观测走时;tjkpre为理论走时;Δv为速度扰动;dl为网格长度;v为初始速度。
对于Pn波射线,采用常规二维Pn波层析成像方法(Hearn,1996;Liang et al,2004;Pei et al,2007;Li et al,2017),将Pn波走时分为3部分,即从震源到莫霍面的走时、沿莫霍面滑行的走时和从莫霍面到台站的走时
| $ {{\mathit{r}}_{\mathit{jk}}}\text{=}\mathit{t}_{\mathit{jk}}^{\text{obs}}\text{-}\mathit{t}_{\mathit{jk}}^{\text{pre}}\text{=}{{\sum\nolimits_{\mathit{m}=1}^{\mathit{n}\text{1}}{\left(-\frac{\text{d}\mathit{l}}{\mathit{v}} \right)\left(\frac{\Delta \mathit{v}}{\mathit{v}} \right)}}_{\mathit{m}}}\text{+}{{\sum\nolimits_{\mathit{e}=1}^{\mathit{n}\text{2}}{\left(-\frac{\text{d}\mathit{l}}{\mathit{v}} \right)\left(\frac{\Delta \mathit{v}}{\mathit{v}} \right)}}_{\mathit{e}}} \\ \text{+}{{\sum\nolimits_{\mathit{r}=1}^{\mathit{n}\text{3}}{\left(-\frac{\text{d}\mathit{l}}{\mathit{v}} \right)\left(\frac{\Delta \mathit{v}}{\mathit{v}} \right)}}_{\mathit{r}}}\text{+ }\!\!\Delta\!\!\text{ }{{\mathit{u}}_{\mathit{k}}}+\text{ }\!\!\Delta\!\!\text{ }{{\mathit{t}}_{\mathit{k}}} $ | (2) |
| $ \text{ }\!\!\Delta\!\!\text{ }{{\mathit{u}}_{\mathit{k}}}\text{=}\sqrt{\frac{\text{1}}{\mathit{v}_{\text{c}}^{2}}\text{-}\frac{\text{1}}{\mathit{v}_{\text{m}}^{2}}}\text{ }\!\!~\!\!\text{ * }\!\!\Delta\!\!\text{ }{{\mathit{h}}_{\mathit{k}}} $ | (3) |
式(2)、(3)中的Δuk为莫霍面深度变化引起的走时变化;Δtk为震源延迟项,主要包括事件深度和开始时刻等引起的震源误差;Δhk为莫霍面深度的变化量;vc、vm分别为地壳底部的速度和上地幔顶部的速度。
初始模型选用的地壳速度为6.3km/s,是由Pg震相时距曲线进行拟合得到的,经过多次试算,最终选取上地幔顶部的速度为8.0km/s、深度为35km的反演结果较为理想。初始模型一共分为8层(含莫霍面),间隔为5km。在进行走时计算时,为了正确区分震相并去除拾取错误的震相,采用了一种自动识别震相的方法。考虑到江苏地区的莫霍面深度在35km内,因此,设置初始距离为0.8°,当震中距小于该值时,只考虑式(1)中地壳Pg波走时的计算;而当震中距大于0.8°时,分别利用式(1)、(2)计算Pg、Pn走时。当单个走时残差大于4s时,则该射线走时不参与反演,同时计算Pg、Pn波震相的走时残差,当两者的残差差值小于0.5s时,也不考虑该走时,最后根据各自走时残差的大小来确定该走时属于哪种震相。
反演方法采用阻尼最小平方法(LSQR)(Paige et al,1982),对式(1)、(2)进行联合求解,使下式达到最小,另外,为了克服方程求解的病态和不稳定性,加入了阻尼因子λ和平滑因子μ
| $ {\text{最小化}}\ \ \ \ \ \ \ \|\mathit{Am}\text{-}\mathit{d}{{\|}^{\text{2}}}\text{+}{{\mathit{\lambda }}^{\text{2}}}\|\mathit{m}{{\|}^{\text{2}}}\text{+}{{\mathit{\mu }}^{\text{2}}}\|\mathit{Lm}{{\|}^{\text{2}}} $ | (4) |
其中,第1项为方程的最小平方残差;第2项为阻尼项,用于控制整个解的稳定性;第3项为平滑项,用于控制相邻网格之间解的平滑性。
2 结果与讨论如图 2(a)所示,目前由于各种原因很多震相数据的走时数据存在各种偏差,这很容易出现震相标识错误,将属于地壳Pg波的震相标识为Pn波震相。由图 2(b)可见,对于Pn、Pg震相走时十分接近的临界距离(震中距120~180km),难以进行有效的筛选;而对于震中距大于300km的震相,利用本文方法能对Pn、Pg震相进行十分有效的筛选识别,这种筛选提高了数据的使用精度,从而有助于提高后续层析成像结果的可靠性。
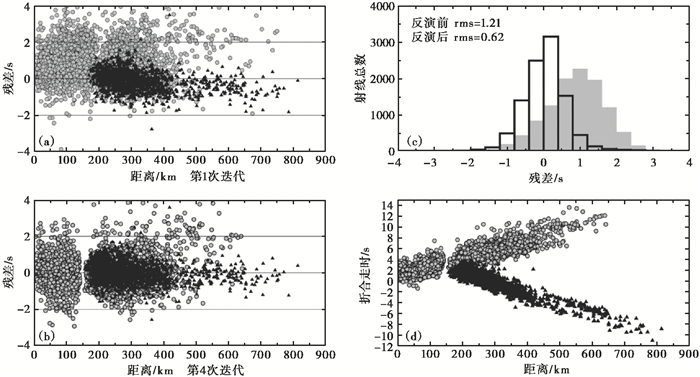
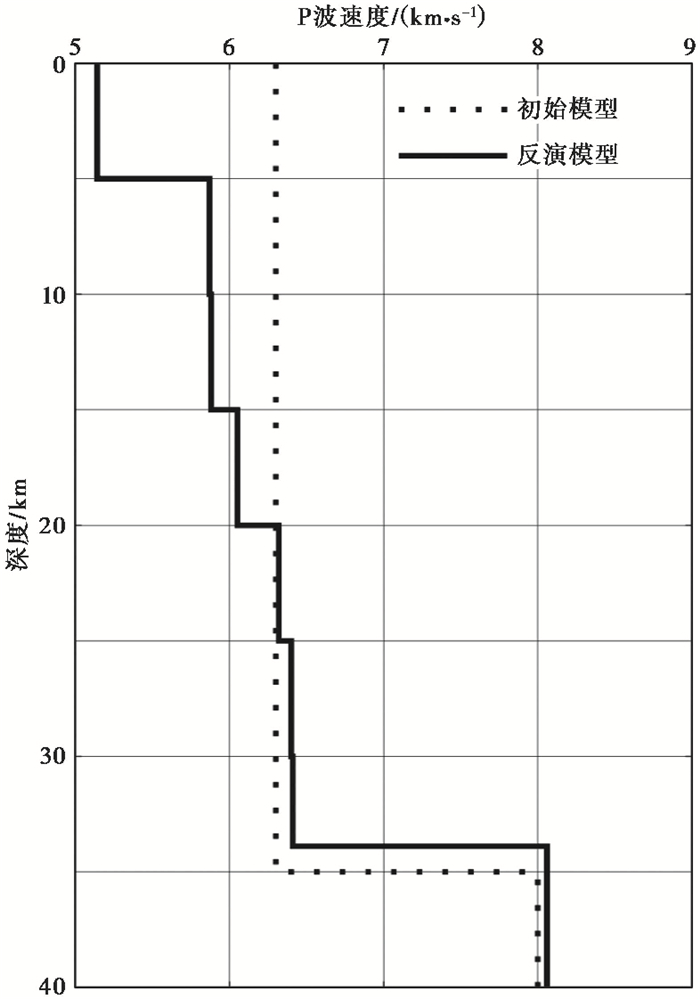
每次联合反演都将上次反演结果作为初始模型进入下一次的联合反演,经过4次迭代,反演结果趋于稳定,走时数据残差的均方根值由1.21s降为0.62s,残差减少了52%,与初始模型残差分布相比,反演后的残差以零值为基线基本呈正态分布(图 3(c)),数据残差减小十分明显。从反演前后的残差与震中距间的关系来看(图 3(a)、3(b)),初始模型的残差对于小震中距震相而言,以正残差为主,说明浅层的速度偏大;而对于大于500km的震中距震相(主要为Pn震相),则以负残差为主,说明初始模型的莫霍面速度偏小;经过反演大、小震中距下的走时残差都得到了有效校正,基本沿残差零值两侧分布。图 3(d)中显示出Pg、Pn波折合走时随震中距的增加震相区分越加明显。图 4为反演前后一维速度模型分布。由图 4可见,反演后的P波速度为5.14~6.41km/s,莫霍面厚度为33.86km,上地幔顶部速度为8.06km/s。其中,浅层0~5km的速度最小,5~15km之间速度变化很小,为5.88km/s;与下地壳相比,中、上地壳20km以内的速度较小,整个地壳的平均速度为6.0km/s,与全球速度模型iasp91相比,显著偏低。
|
图 3 反演前后残差分布 (a)初始模型的残差分布;(b)最终模型的残差分布;(c)反演前、后残差直方图;(d)反演后的折合走时(T-X/7)黑色实心三角代表Pn波震相;灰色圆圈代表Pg波震相;rms为残差均方根 |
|
图 4 反演前后一维速度模型分布 |
由于阻尼最小平方法(LSQR)不能对反演结果给出误差估计,因此,本文采用常规Bootstrap方法对所有数据进行随机采样并进行相同参数下的反演,重复100次得到本次反演模型的误差估计值。地壳不同深度下的速度误差分别为0.036km/s(0km)、0.028km/s(5km)、0.022km/s(10km)、0.025km/s(15km)、0.018km/s(20km)、0.013km/s(25km)、0.052km/s(30km);上地幔顶部速度和莫霍面深度的误差分别为0.0035km/s、0.114km。
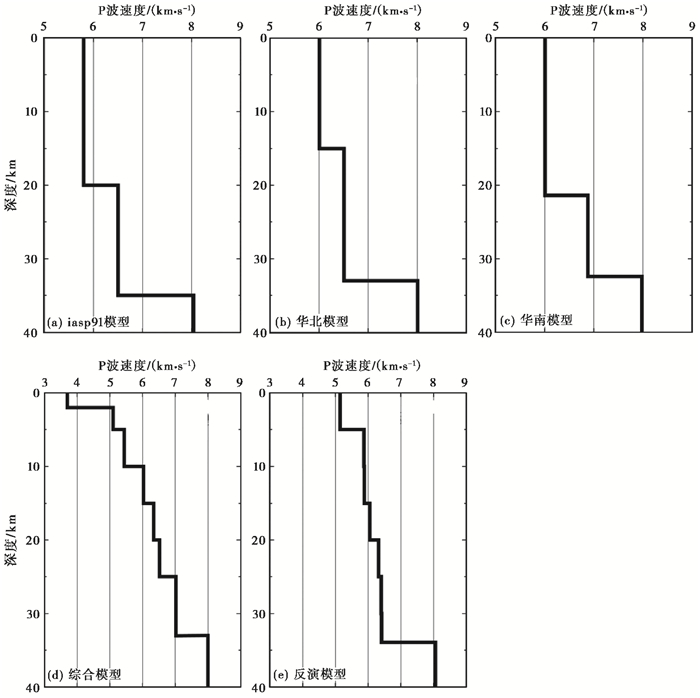
为了探讨该模型是否对江苏地区具有一定的代表性,选取了目前江苏及其邻区常用的几种模型(图 5),计算相同地震数据下不同模型的残差结果并对其进行简单比较。此次一维P波速度模型只包括地壳、上地幔顶部的速度以及莫霍面深度参数。选取的模型中用于日常定位的有3种,分别为iasp91全球模型、华北模型和华南模型等;用于层析成像的模型主要来自于HQ13测线(综合模型)(黄耘等,2011)。定位模型中,iasp91模型是目前江苏台网日常使用的,而华南模型目前在相邻的安徽地区作为地震定位速度模型使用(谢石文等,2016)。
|
图 5 研究区4种一维P波速度模型与反演速度模型对比 |
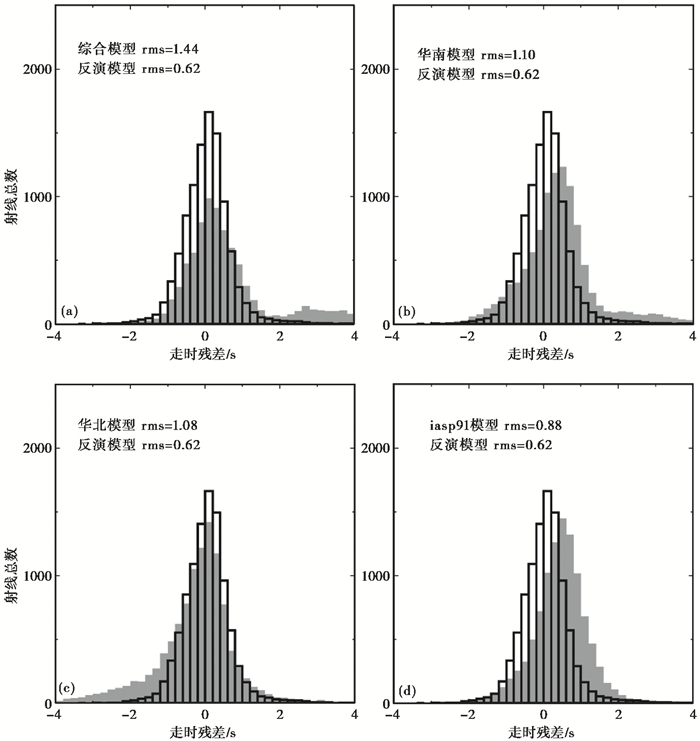
几种模型中,iasp91模型属于全球速度模型,华北模型和华南模型主要是针对特定地区地震定位的模型,因此,这几种模型的应用范围并不能代表江苏地区的速度模型。由几种模型计算得到的所有残差均方根值可见,本文反演的一维P波速度模型残差均方根最小;深地震反射获取的速度模型(综合模型)的残差最大,这可能说明江苏地区具有较为复杂的地质构造分布,单一的反射剖面不能很好地约束整个区域的地震走时。我们将此次反演模型与其他模型的结果进行比较,结果如图 6所示。由图 6可见,深地震反射速度模型能拟合的数据最少且残差最大,其次为华南模型,然后是华北模型,最好的是iasp91模型。iasp91模型的走时残差均方根值为0.88s,比此次反演模型的多近30%。由此可见,本文采用的联合反演获取的一维P波速度模型对初至波、续至波震相数据拟合最好。
|
图 6 研究区4种一维P波速度模型与反演模型的残差分布 走时残差为观测走时与不同模型下理论走时的残差;rms为残差均方根 |
本文利用地震走时数据采用联合反演方法获取了江苏地区的一维P波速度模型,得到以下认识。
(1) 与仅采用初至波走时的传统天然地震走时获取方法相比,该方法同时使用初至波、续至波震相走时,充分利用了大量存在的续至波参与反演,能有效提高中下地壳的反演能力。针对常规地震震相目录中常存在的震相标识错误问题,采用的自动判别筛选震相方法能最大限度提高数据走时的精度,可以对不同震相进行有效区分。
(2) 通过与其他速度模型进行简单比较,反演模型对Pg、Pn震相走时拟合效果最佳,具有最小的残差。当所用走时数据定位精度较高时,该联合反演方法能为研究区三维速度结构成像和地震定位提供较可靠的一维速度模型。此外,目前各台网使用诸如华南或华北等模型作为地震定位的一维速度模型,尽管它们是简单的二层速度模型,但却有较高的定位效率。而本方法速度模型是多层的,后续工作将对该模型作进一步改进,并考虑运用爆破地震来有效检验该模型的定位能力。
| 白志明, 王椿镛. 2006, 下扬子地壳P波速度结构符离集——奉贤地震测深剖面再解释. 科学通报, 51(21): 2535–2539. |
| 黄耘, 李清河, 张元生, 等. 2011, 郯庐断裂带鲁苏皖段及邻区地壳速度结构. 地球物理学报, 54(10): 2549–2555. DOI:10.3969/j.issn.0001-5733.2011.10.012 |
| 柯乃琛, 华卫. 2016, 小湾水库库区最小一维速度模型研究. 地震, 36(2): 38–47. |
| 李铂, 崔鑫, 叶庆东, 等. 2012, 山东地区地震波一维速度模型研究. .华北地震科学(4): 1–6. |
| 田玥, 陈晓非. 2006, 利用拟牛顿法和信赖域法联合反演震中分布与一维速度结构. 地球物理学报, 49(3): 845–854. |
| 王小娜, 于湘伟, 章文波, 等. 2015, 龙门山断裂带南段地壳一维P波速度结构. 地震研究, 38(1): 16–24. |
| 王有学, 姜枚, 韩国华. 2004, 中国大陆科学钻探场址区的地壳速度结构特征. 地球科学, 27(6): 668–672. |
| 谢石文, 韩成成, 郁建芳, 等. 2016, 基于Hyposat定位法的安徽地区地壳一维速度模型研究. 地球物理学进展, 31(6): 2429–2437. DOI:10.6038/pg20160610 |
| 徐纪人, 杨文采, 赵志新, 等. 2003, 苏鲁大别造山带岩石圈三维P波速度结构特征. 地质学报, 77(4): 578–582. |
| 徐佩芬, 刘福田, 王清晨, 等. 2000, 大别-苏鲁碰撞造山带的地震层析成像研究岩石圈三维速度结构. 地球物理学报, 43(3): 378–382. |
| 杨文采, 陈国九. 1999a, 苏鲁超高压变质带北部地球物理调查(Ⅰ):深反射地震. 地球物理学报, 42(1): 41–52. |
| 杨文采, 胡振远, 程振炎, 等. 1999b, 郯城-涟水综合地球物理剖面. 地球物理学报, 42(2): 207–210. |
| 于湘伟, 陈运泰, 王培德. 2003, 京津唐地区中上地壳三维P波速度结构. 地震学报, 25(1): 1–14. |
| 赵旭, 李强, 蔡晋安. 2007, 三峡库首区最小一维速度模型研究. 大地测量与地球动力学, 27(增刊Ⅰ): 1–7. |
| Hearn T M. 1996, Anisotropy Pn tomography in the west United States. J Geophys Res, 101: 8403–8414. DOI:10.1029/96JB00114. |
| Kissling E, Ellsworth W L, Eberhart-Phillips D, et al. 1994, Initial reference models in local earthquake tomography. J Geophys Res, 99(B10): 19635–19646. DOI:10.1029/93JB03138. |
| Koketsu K, Sekine S. 1998, Pseudo-bending method for three-dimensional seismic ray tracing in a spherical earth with discontinuities. Geophys J Int, 132(2): 339–346. DOI:10.1046/j.1365-246x.1998.00427.x. |
| Li X B, Song X D, Li J T. 2017, Pn tomography of South China Sea, Taiwan Island, Philippine archipelago, and adjacent regions. J Geophys Res, 122(2): 1350–1366. DOI:10.1002/jgrb.v122.2. |
| Liang C, Song X D, Huang J. 2004, Tomographic inversion of Pn travel times in China. J Geophys Res, 109(B11): 285–296. |
| Paige C C, Saunders M A. 1982, LSQR:Sparse linear equations and least squares problems. Acm Trans Math Software, 8(2): 195–209. DOI:10.1145/355993.356000. |
| Pei S P, Zhao J M, Sun Y S, et al. 2007, Upper mantle seismic velocities and anisotropy in China determined through Pn and Sn tomography. J Geophys Res, 112(B5): 622–634. |
| Shearer P M, 2009, Introduction to seismology, 103~110, Oxford: Cambridge University Press. |
| Xu Z J, Song X D. 2010, Joint inversion for crustal and Pn velocities and Moho depth in eastern margin of the Tibetan Plateau. Tectonophysics, 491: 185–193. DOI:10.1016/j.tecto.2009.11.022. |