在场地地震反应计算中,剪切波速测试误差对地表地震动参数有重要影响,而剪切波速的测量不可避免地存在误差,误差可能会达到30%左右(薄景山等,2003;兰景岩等,2007;彭艳菊等,2011)。有学者曾在全国范围内通过抽样开展了现场剪切波速实测误差统计实验,得出4种类别场地的波速测试误差符合正态分布,不同场地类别、不同测试深度的剪切波速测试误差水平基本相当,约95%的波速测试结果位于均值的2倍误差标准差(30%)范围内(陈卓识,2015)。
一些学者开展了不同的数值模拟实验研究剪切波速的误差对土层地震反应计算结果的影响。孙锐等(2009)研究了剪切波速对场地地震动的影响以及与动剪切模量比的等量关系。沈得秀等(2014)将土层按深度分段,每个分段给出一组剪切波速的改变量,分析了在不同深度段、不同概率水平下土层剪切波速的变化对场地地震动参数的影响。兰景岩等(2007)研究了单一均质的土层剪切波速的不确定性对设计反应谱的影响。刘宇(2013)研究了在单层土和双层土模型情况下剪切波速对地震动参数的影响。李平等(2010)研究了在粘性土和砂土土层模型中剪切波速变化对地表地震动参数的影响。
然而,现有研究所开展的数值模拟中设计波速误差的方式或者设计的土层模型与实际情况差别较大。有的是使用假定的土层模型,有的是对所有土层的波速都调整,有的是按厚度分区间调整。在实际情况中,每个土层的剪切波速误差并不是有规律的、一致的变化,而是每层土的波速误差都随机出现。为避免此类问题,更好地贴近实际情况来研究剪切波速的误差对地震动参数的影响,本文基于蒙特卡洛模拟计算原理(Bazzurro,2004;Rong et al,2016),使用一系列实测土层模型,将每个土层模型中每层土层波速误差的出现设定为随机的。本文共搜集分布在山东地区的132个场地钻孔数据开展蒙特卡洛方法研究,这些钻孔较均匀地分布在全省范围内,对山东省的钻孔数据有较好的代表性。
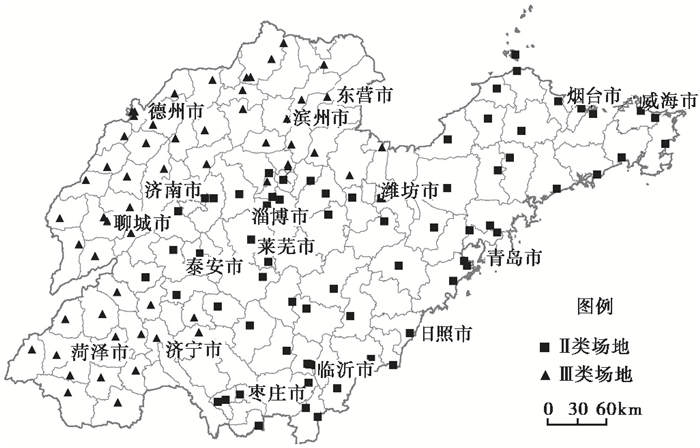
1 资料收集与整理山东省境内工程场地类别绝大多数是Ⅰ ~ Ⅲ类场地(蒋其峰等,2017),而Ⅰ类场地属于基岩场地,不参与场地地震反应计算,所以本文仅对Ⅱ类场地和Ⅲ类场地进行研究探讨。本文搜集了山东省境内空间位置分布较为均匀的132处工程场地的钻孔资料以及动三轴测试数据等,工程场地的空间分布情况见图 1。由于钻孔分布较均匀,所以从抽样角度来看对山东省工程场地土层结构情况具有较好的代表性。根据《GB 50011-2010建筑抗震设计规范(2016年版)》(中华人民共和国住房和城乡建设部等,2010)中场地类别划分方法,132个场地中有71个Ⅱ类场地、61个Ⅲ类场地。
|
图 1 研究范围工程场地的分布情况 |
蒙特卡洛方法是一种随机模拟方法,将一系列随机数当作样本进行模拟实验,并对实验结果进行总结以获取问题的解,随机样本越多,则越接近正确的解。剪切波速的测试误差是随机出现的,符合随机模拟的特点,因此可进行蒙特卡洛随机模拟。土层地震反应计算采用等效线性化方法,即用等效线性化的处理手段将复杂的非线性土层反应计算等效为线性计算(廖振鹏,1989)。输入地震动时程根据山东地区的地震危险性水平合成对应大震、中震、小震3种概率水准的时程,同一概率水准下合成3条随机相位的地震动时程,共合成了9条地震动时程。根据132处工程场地的钻孔资料,共建立132个钻孔计算模型。对于每一个场地钻孔模型,除了进行1次土层地震反应计算外,根据蒙特卡洛随机模拟原理,在实测剪切波速值30%偏差的范围内随机生成100组剪切波速值,然后分别用这100组模拟剪切波速构建土层模型,分别进行土层地震反应计算,即基于每个钻孔模型共进行101次土层地震反应计算。数值实验中设计的剪切波速值30%的偏差范围是根据部分学者的研究得出的(薄景山等,2003;兰景岩等,2007;陈卓识,2015)。每个钻孔模型的每次土层地震反应计算都利用9条输入地震动时程,每个钻孔模型共有909种计算工况,对所有132个钻孔模型共计算了119988种工况,计算得到每个场地909种工况的加速度反应谱。表 1给出了2个典型场地实测钻孔模型,其中,模型1为Ⅲ类场地,模型2为Ⅱ类场地,表 2给出了相应的土动力学参数。
| 表 1 典型场地实测钻孔模型 |
| 表 2 典型场地的土动力学参数 |
经过对每个场地用实测波速和带随机误差的100组模拟波速构建的101个土层模型的土层地震反应计算,每个场地得到3种概率水准下共909条反应谱,132个场地共得到119988条反应谱。
为了探讨剪切波速误差变化对反应谱的影响,需要对反应谱的偏差进行定量分析,本文计算了每个场地反应谱的相对偏差。如果将实测波速计算得到的反应谱记为RS0(t)(0≤t≤6.0s),将含随机误差的模拟剪切波速的场地模型计算得到的反应谱记为RSi(t)(0≤t≤6.0s,i=1,2,3…100),将反应谱相对偏差记为RSpi(t)(0≤t≤6.0s,i=1,2,3…100),那么反应谱相对偏差的计算公式如下
| $ {\rm{R}}{{\rm{S}}_{pi}}\left(t \right) = \left[ {{\rm{R}}{{\rm{S}}_i}\left(t \right) - {\rm{R}}{{\rm{S}}_0}\left(t \right)} \right]/{\rm{R}}{{\rm{S}}_{\rm{0}}}\left(t \right)\left({0 \le t \le 6.0{\rm{s, }}\;i = 1, 2, 3 \cdots 100} \right) $ | (1) |
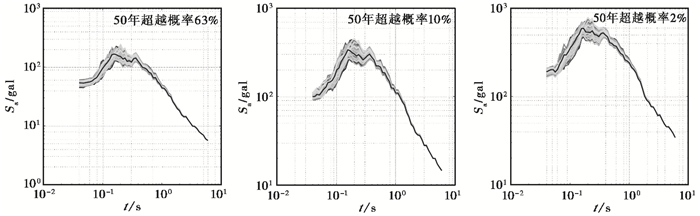
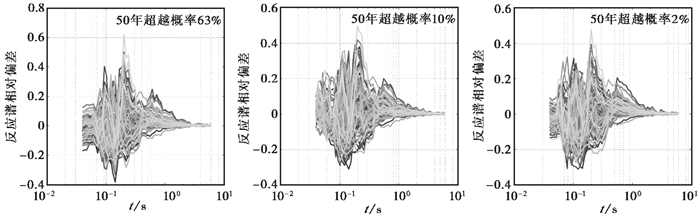
图 2给出了某工程场地在输入地震动时程为相位1时在不同概率水准下的反应谱计算结果,图 3给出了该场地在输入地震动时程为相位1时在不同概率水准下的反应谱相对偏差计算结果。
|
图 2 某工程场地反应谱计算结果 黑色线为RS0(t) |
|
图 3 某工程场地反应谱相对偏差计算结果 |
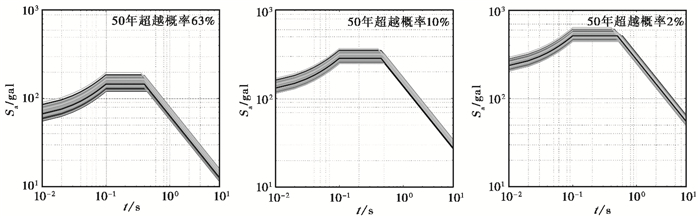
为更进一步分析反应谱的变化,本文按照《GB 18306-2015〈中国地震动参数区划图〉宣贯教材》(高孟潭,2015)中提供的规准反应谱公式(式(2))对计算得到的反应谱进行了规准化。每个场地得到303条规准反应谱,132个场地共得到39996条规准反应谱,其中某工程场地的规准反应谱计算结果见图 4。
| $ {S_{\rm{a}}}\left( T \right) = \left\{ \begin{array}{l} {a_m} + {a_m}\left( {{\beta _m} - 1.0} \right)\frac{T}{{{T_0}}}\;\;\;\;0.0 < T < {T_0}\\ {a_m}{\beta _m}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{T_0} < T \le {T_g}\\ {a_m}{\beta _m}{\left( {\frac{{{T_g}}}{T}} \right)^\alpha }\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{T_g} < T \le {T_m} \end{array} \right. $ | (2) |
|
图 4 某工程场地规准反应谱计算结果 黑色线为RS0(t)的规准谱 |
式(2)中,am、βm、T0、Tg、α分别表示设计地震动峰值加速度、放大系数反应谱平台值、第一拐点周期值、特征周期值、下降段控制参数,amβm即为规准反应谱平台值。根据式(2),规准反应谱的平台值和特征周期是描述规准反应谱的2个关键参数,于是本文计算了规准反应谱平台值和特征周期值的相对偏差,用来描述规准反应谱的变化。如果将实测波速计算得到的规准反应谱的平台值和特征周期分别记为A0和Tg0,将含随机误差的模拟波速计算得到的规准反应谱的平台值和特征周期分别记为Ai和Tgi (i=1,2,3…100),将规准反应谱平台值和特征周期的相对偏差分别记为Api 和Tgpi (i=1,2,3…100),那么规准反应谱平台值和特征周期的相对偏差的计算公式如下
| $ {A_{pi}} = \left({{A_i} - {A_0}} \right)/{A_0} $ | (3) |
| $ {T_{gpi}} = \left({{T_{gi}} - {T_{g0}}} \right)/{T_{g0}} $ | (4) |
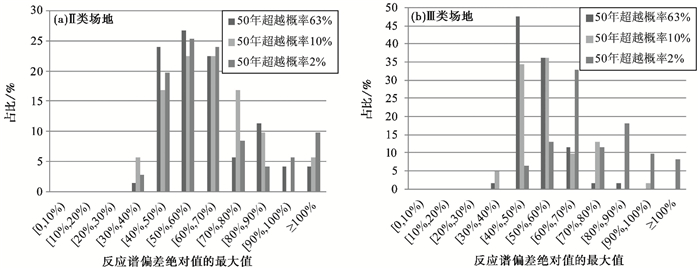
经过上述计算,每个场地都得到100组反应谱相对偏差RSpi (t)(0≤t≤6.0s,i=1,2,3…100)、100组反应谱平台值相对偏差Api (i=1,2,3…100)和100组特征周期相对偏差Tgpi (i=1,2,3…100),为研究剪切波速变化对反应谱的最大影响,本文求取每个场地3个概率水准下反应谱相对偏差RSpi (t)(0≤t≤6.0s,i=1,2,3…100)、反应谱平台值相对偏差Api (i=1,2,3…100)、特征周期相对偏差Tgpi (i=1,2,3…100)的绝对值的最大值,依次记为|RSpi(t)|max(0≤t≤6.0s,i=1,2,3…100)、|Api|max(i=1,2,3…100)、|Tgpi|max(i=1,2,3…100),并对所有场地按照场地类别进行分类统计,计算分布在不同的反应谱相对偏差的绝对值的最大值|RSpi (t)|max(0≤t≤6.0s,i=1,2,3…100)的取值范围的场地个数占场地总数的比例(图 5)、分布在不同的反应谱平台值相对偏差绝对值的最大值|Api|max(i=1,2,3…100)的取值范围的场地个数占场地总数的比例(图 6),以及分布在不同的特征周期相对偏差的绝对值的最大值|Tgpi|max(i=1,2,3…100)的取值范围的场地个数占场地总数的比例(图 7)。
|
图 5 反应谱偏差绝对值的最大值|RSpi(t)|max在不同取值范围的占比情况 |
|
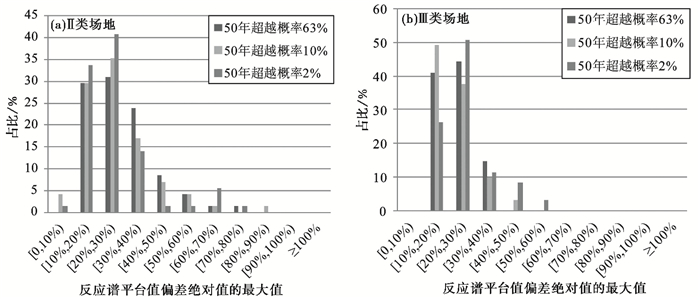
图 6 反应谱平台值偏差绝对值的最大值|Api|max在不同取值范围的占比情况 |
|
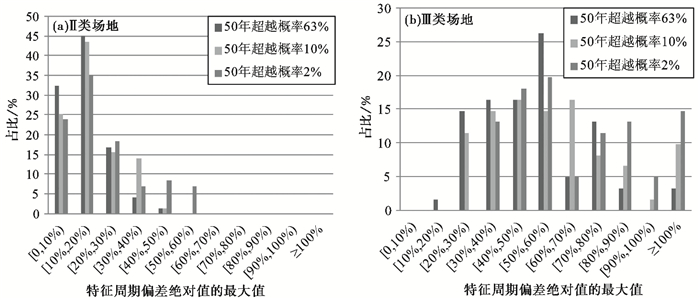
图 7 特征周期偏差绝对值的最大值|Tgpi|max在不同取值范围的占比情况 |
根据反应谱偏差绝对值的最大值|RSpi(t)|max计算结果(图 5),Ⅱ类场地和Ⅲ类场地反应谱偏差绝对值的最大值都在30%以上,最大可达100%以上。与50年超越概率63%、10%两个概率水准相比,在50年超越概率2%的概率水准下,反应谱偏差绝对值的最大值大于100%的几率较大。此外,经过与特征周期的对比发现,反应谱偏差绝对值的最大值对应的周期值大多小于特征周期。以上结果分析表明,30%以内的随机波速误差会导致某些周期处的反应谱的变化达30%以上,最高影响大于100%,输入地震动越大,出现高影响值的可能性越大。此外,影响最大的反应谱值大多出现在小于特征周期的频段内。
根据反应谱平台值偏差绝对值的最大值|Api|max计算结果(图 6),对于Ⅱ类场地,反应谱平台值偏差绝对值的最大值在0~90%范围内均有分布,优势分布为10%~50%。对于Ⅲ类场地,反应谱平台值偏差绝对值的最大值优势分布为10%~50%,以上结果分析表明,30%以内的随机波速误差对反应谱平台值最大的影响大多在10%~50%之间。
根据特征周期偏差绝对值的最大值|Tgpi|max计算结果(图 7),总体而言,Ⅲ类场地比Ⅱ类场地的特征周期偏差绝对值的最大值分布更加离散,说明剪切波速误差对Ⅲ类场地反应谱特征周期影响更显著。对于Ⅱ类场地,特征周期偏差绝对值的最大值优势分布范围为0~50%;对于Ⅲ类场地,特征周期偏差绝对值的最大值分布离散性较大,最高可达100%以上,优势分布在20%~90%之间。上述结果分析表明,30%以内的随机波速误差对Ⅲ类场地特征周期的影响比Ⅱ类场地大,对Ⅱ类场地特征周期的最大影响大多在0~50%之间,对Ⅲ类场地特征周期的最大影响则大多在20%~90%之间。输入地震动越大,出现高影响值的可能性越大。
5 结论本文搜集了在山东省境内分布较均匀的132处工程场地的钻孔资料,建立相应的钻孔模型,基于蒙特卡洛随机模拟的原理,对每一钻孔模型在30%的误差范围内随机生成了100组剪切波速,根据山东省的地震危险性特征,合成大、中、小3个强度水平的地震输入,分别进行场地地震反应计算。通过对随机模拟值与实测值计算结果的相对偏差的计算分析,得到如下结论:
(1) 30%以内的随机波速误差会导致某些周期处的反应谱的变化达30%以上,最高影响大于100%,输入地震动越大,出现高影响值的可能性越大,这些受影响最大的反应谱值所在的周期往往小于特征周期。
(2) 30%以内的随机波速误差对反应谱平台值最大的影响大多在10%~50%之间。
(3) 30%以内的随机波速误差对Ⅲ类场地特征周期的影响比Ⅱ类场地大,对Ⅱ类场地特征周期的最大影响大多在0~50%之间,对Ⅲ类场地特征周期的最大影响则大多在20%~90%之间。
薄景山、李秀领、李山有, 2003, 场地条件对地震动影响研究的若干进展, 世界地震工程, 19(2): 11-15. DOI:10.3969/j.issn.1007-6069.2003.02.002 |
陈卓识, 2015, 现场剪切波速测试误差及其对地震动影响研究, 博士学位论文, 北京: 中国地震局工程力学研究所. http://cdmd.cnki.com.cn/Article/CDMD-85406-1015652708.htm
|
高孟潭, 2015, GB 18306-2015《中国地震动参数区划图》宣贯教材, 北京: 中国质检出版社.
|
蒋其峰、魏玮、王红卫等, 2017, 山东省场地类别分布及地震动峰值加速度区划调整, 震灾防御技术, 12(3): 501-510. |
兰景岩、薄景山、吕悦军, 2007, 剪切波速对设计反应谱的影响研究, 震灾防御技术, 2(1): 19-24. DOI:10.3969/j.issn.1673-5722.2007.01.003 |
李平、薄景山、孙有为, 2010, 剪切波速差异性对地震反应的影响, 世界地震工程, 26(增刊): 133-137. |
廖振鹏, 1989, 地震小区划, 北京: 地震出版社.
|
刘宇, 2013, 剪切波速的不确定性对设计地震动参数的影响, 硕士学位论文, 北京: 中国地震局工程力学研究所. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D370635
|
彭艳菊、吕悅军、施春花等, 2011, 北京平原区基于第四纪地质与剪切波速的场地类别划分, 防灾减灾工程学报, 31(增刊): 108-114. |
沈得秀、王庆民、许洪泰等, 2014, 土层剪切波速测试中的不确定性对场地地震动参数的影响分析——以Ⅲ类场地为例, 震灾防御技术, 9(2): 244-251. DOI:10.3969/j.issn.1673-5722.2014.02.009 |
孙锐、袁晓铭、刘晓键, 2009, 动剪切模量比与剪切波速对地震动影响及等量关系研究, 岩土工程学报, 31(8): 1267-1274. DOI:10.3321/j.issn:1000-4548.2009.08.018 |
中华人民共和国住房和城乡建设部、中华人民共和国国家质量监督检验检疫总局, 2010, GB 50011-2010建筑抗震设计规范(2016年版), 北京: 中国建筑工业出版社.
|
Bazzurro P, 2004, Ground-motion amplification in nonlinear soil sites with uncertain properties, Bull Seismol Soc Am, 94(6): 2090-2109. DOI:10.1785/0120030215 |
Rong M S, Wang Z M, Woolery E W, et al, 2016, Nonlinear site response from the strong ground-motion recordings in western China, Soil Dyn Earth Eng, 82: 99-110. DOI:10.1016/j.soildyn.2015.12.001 |
 2018, Vol. 34
2018, Vol. 34


