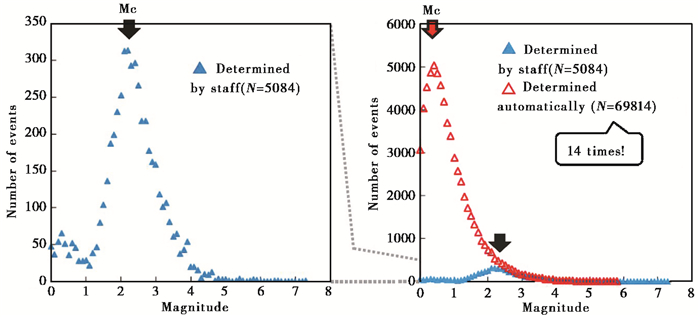
地震事件的识别与拾取是地震数据处理过程中非常重要的一步, 拾取方法的优劣关系着事件拾取的精度、拾取的效率, 好的拾取方法不仅可以提高地震学研究效率, 而且还能促进地震速报、地震预警等防震减灾工作的进步。起初, 地震工作者在进行地震数据处理时, 主要通过人工肉眼分析震相来识别地震事件, 这种方法效率低下, 并且容易出现人为性疏漏。随着地震台网越来越密集, 数据量越来越庞大, 人工拾取地震事件的质量和效率已远远不能满足地震数据处理的需求。另外, 随着地震学的发展, 其研究对象已不仅局限于较大震级地震, 对于微小震级地震事件的研究也不断深入, 这也对能有效识别微小地震的地震事件拾取技术提出了更高的要求, 即需要效率更高、精度更高、错误更少的自动识别地震事件技术。图 1为Tamaribuchi等(2016)在研究熊本地震过程中自动拾取震相与人工拾取震相的对比图。由图 1可见, 自动拾取事件数量与人工拾取数量之比高达14, 并且对于微地震有更强大的识别能力, 而对于这些微震, 人工拾取往往难以分辨, Tamaribuchi等(2016)的研究表明, 发展自动震相拾取技术是地震学发展的必经之路。
|
图 1 自动拾取震相与人工拾取震相对比(据Tamaribuchi等(2016)) |
20世纪70年代以来, 自动识别地震事件和自动拾取震相的方法越来越丰富, 也越来越成熟。无论是对于流动台网还是固定台网的地震数据, 其应用都越来越广泛。最初的震相拾取是通过长短时窗的比值检测来进行的(Stevenson, 1976), 其后, Allen(1978)用其他特征函数代替原始序列提高了精度;之后又有学者提出不同形式的特征函数, 这进一步提高了震相识别的精度(高淑芳等, 2008;余建华等, 2011)。赤池准则法最早由Sleeman等(1999)应用于地震信号的识别, 后来, 刘希强等(2009)、赵大鹏等(2013)分别用偏斜度和峰度代替方差, 取得了较好的结果。Schaff等(2004)对重复地震给出了实际操作层面的定义, 之后模板匹配技术蓬勃发展, 有研究者将其应用到2008年汶川8.0级地震和2015年滦县震群(最大震级ML3.2, 在1976年唐山地震余震区内)中, 均取得了较好结果(吕鹏等, 2011;谭毅培等, 2016)。Brown等(2008)为了避免震相拾取对模板信息的依赖, 提出了基于自相关的彻底盲搜索算法。Yoon等(2015)又将LSH(locality sensitive hashing)算法与震相拾取相结合, 提出了FAST(fingerprint and similarity thresholding)算法, 该算法避免了计算量大的问题。也有学者试图将神经网络引入到地震学研究中来(Dai et al, 1997;裴正林等, 1999;王金峰等, 2006)。马强等(2013)已在福建省地震预警实验系统中应用Delaunay三角剖分法来剔除非几何相关的干扰信号。近年来, Grigoli等(2018)的全波形叠加、何先龙等(2016)的二次方自回归以及Lomax等(2012)的多频率震相识别等方法均在拾取精度或运算速度上有所突破。
本文总结了目前常用的几种震相识别技术, 如长短时窗法、赤池准则法、基于互相关的模板匹配滤波法、基于自相关盲搜索的FAST法、对于S波震相拾取的偏振分析法、神经网络等, 以及近几年发展起来的全波形叠加、多频率震相识别等在地震学中的应用, 并分析了每种方法的优势和局限性, 以期为震相自动拾取方面的研究提供相关信息。
1 震相自动拾取技术简介震相拾取方法种类很多, 我们主要通过2个指标来评价某个方法的优劣:一是精度, 这要求拾取震相精确可靠, 也包括在低信噪比下的适用性;二是效率, 要有足够的效率以满足需求。以下在介绍具体方法时也从这2个方面进行评价。事实上, 没有哪个方法能完美地同时满足精度和效率, 而将不同方法的优势结合、劣势互补就显得尤为重要。下面分别介绍震相的拾取过程及方法。
1.1 长短时窗法长短时窗法最早由Stevenso(1976)提出。缩写为STA/LTA法, STA为短时窗平均值, LTA为长时窗平均值, 两者之间比值的变化可以反映信号能量的变化。STA、LTA分别表示如下
| $ {\rm{ST}}{{\rm{A}}_j} = \frac{{\sum\limits_{n = i - N + 1}^i {Y\left( n \right)} }}{N} $ | (1) |
| $ {\rm{LT}}{{\rm{A}}_i} = \frac{{\sum\limits_{n = i - M + 1}^i {Y\left( n \right)} }}{M} $ | (2) |
| $ R = \frac{{{\rm{ST}}{{\rm{A}}_i}}}{{{\rm{LT}}{{\rm{A}}_i}}} $ | (3) |
M、N为采样点数;R为长短时窗比。当STA比LTA变化大时, R显著增大, 这表明有信号突变, 此时通过设定好的阈值便可判断是否为地震事件。早期的地震事件拾取工作直接利用原始的地震序列, 结果并不是很好, 后来选择其他特征值代替进行计算, 特征值选取可有以下几种
| $ {\rm{C}}{{\rm{F}}_1}\left( i \right) = Y{\left( i \right)^2} $ | (4) |
| $ {\rm{C}}{{\rm{F}}_2}\left( i \right) = \left| {Y\left( i \right) - Y\left( {i - 1} \right)} \right| $ | (5) |
| $ {\rm{C}}{{\rm{F}}_3}\left( i \right) = Y{\left( i \right)^2} + {\left[ {Y\left( i \right) - Y\left( {i - 1} \right)} \right]^2} $ | (6) |
| $ {\rm{C}}{{\rm{F}}_4}\left( i \right) = Y{\left( i \right)^2} - Y\left( {i - 1} \right)Y\left( {i + 1} \right) $ | (7) |
|
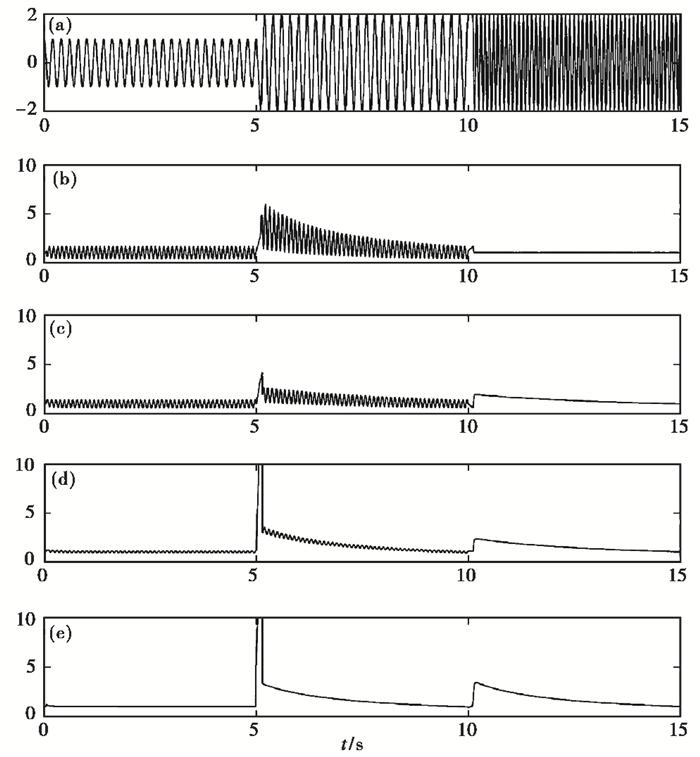
图 2 4种特征函数效果(据蒋策(2017)) 图(a)为原始余弦信号, 前2段频率相同振幅不同, 后2段振幅相同频率不同;图(b)~(e)对应式(4)~(7)不同特征值 |
长短时窗法是一种操作简单、计算速度较高的方法, 它不依赖于模板, 拥有广泛的适用空间。然而, 其对信噪比较为敏感, 在低信噪比及高频脉冲的影响下, 长短时窗法只能拾取地震事件的大致到时, 甚至会拾错和误判。所以, 实际工作中先使用长短时窗法得到粗略的到时来缩小范围, 再采用其他方法使结果更加精确。
1.2 赤池准则法赤池信息准则(Akaike information criterion, AIC)最初用于统计学, 是统计模型拟合度的衡量标准, 由日本统计学家赤池弘次创立和发展。赤池函数表示为
| $ {\rm{AIC}} = 2k - 2\ln L $ | (8) |
Sleeman等(1999)将赤池函数引入地震学, 他认为以突变时刻n作为分界点的话, 地震信号可视为2个完全不同的趋于稳态的模型, 然后分别计算突变前后的AIC函数值, 不断调整n, 使AIC值最小的模型则被认为是最佳模型, 而此时的n即被视为初动到时
| $ {\rm{AIC}}\left( n \right) = \left( {n - M} \right)\ln \sigma _1^2 + \left( {N - n + M} \right)\ln \sigma _2^2 + c $ | (9) |
其中, N为信号总长度;M为自回归阶数;n为分界点;σ1、σ2分别为前后2个模型的方差。
引入数学中高阶统计量与赤池准则进行结合判定, 数学期望为一阶统计量, 方差为二阶, 偏斜度为三阶, 峰度为四阶, 表达式分别如下
| $ {m_k} = E\left\{ {{{\left[ {x - E\left( x \right)} \right]}^k}} \right\} $ | (10) |
| $ S = \frac{{{m_3}}}{{{{\left( {{m_2}} \right)}^{2/3}}}} $ | (11) |
| $ k = \frac{{{m_4}}}{{{{\left( {{m_2}} \right)}^2}}} $ | (12) |
| $ {\rm{VAR\_AIC}} = k\lg \left\{ {{\mathop{\rm var}} \left[ {x\left( {1,k} \right)} \right]} \right\} + \left( {N - k - 1} \right)\lg \left\{ {{\mathop{\rm var}} \left[ {x\left( {k + 1,N} \right)} \right]} \right\} $ | (13) |
刘希强等(2009)、赵大鹏等(2013)将式(10)~(13)中方差替代为偏斜度和峰度, 得出在信噪比不高的情况下由偏斜度和峰度得到的结果较由方差得到的结果更精确的结论。沈统等(2017)利用三分量微震数据协方差矩阵对AIC方法进行约束, 提高了计算精度。其中, 赵大鹏等(2013)用2个时间段数据的峰度作为特征函数的方法, 被称为Kurtosis-AIC方法, 表示为
| $ {\rm{Kurtosis - AIC}}\left( k \right) = k\lg \left( {\frac{1}{k}\sum\limits_{j = 1}^k {{\rm{CF}}_j^2} } \right) + \left( {L - k + 1} \right)\lg \left( {\frac{1}{{L - k + 1}}\sum\limits_{j = k}^l {{\rm{CF}}_j^2} } \right) $ | (14) |
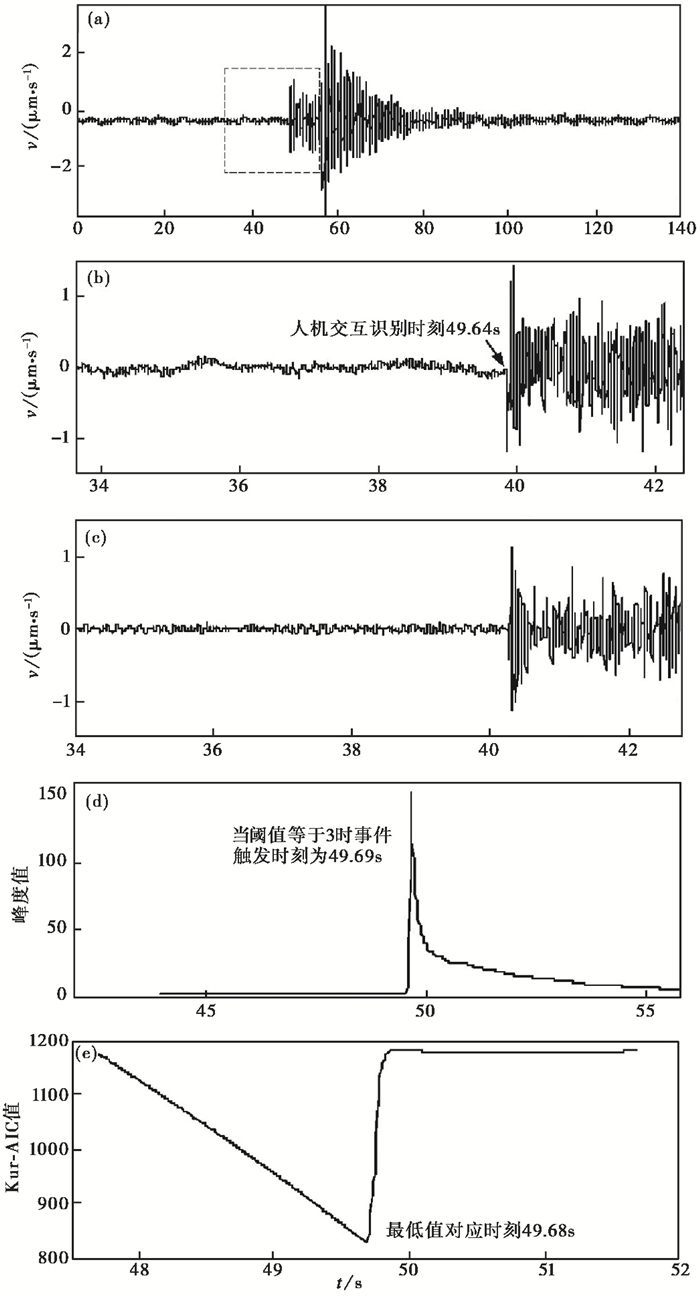
其中, L为特征函数的长度;k取值为1~L。图 3为效果图。
|
图 3 峰度作为特征值的Kurtosis-AIC方法在2009年梁山台记录地震中的应用(据赵大鹏等(2013)) (a)垂直向记录;(b)图(a)的虚框放大图;(c)对图(b)的滤波结果;(d)峰度曲线;(e)Kurtosis-AIC变化曲线 |
模板匹配技术(matched filter technique)是基于滑动互相关技术发展起来的, Gibbons等(2006)在研究1997年Kara Sea地震的1次mb3.5余震的过程中发现, 传统的长短时窗方法无法检测到的微震可以通过模板匹配方法识别出来。Kato等(2014)利用模板匹配技术对2014年智利8.1级地震的研究得到了10倍于传统方法拾取的地震事件数。
模板匹配技术通过计算地震波形与模板事件的互相关来衡量二者的相似程度, 从而判断地震事件, 因此对模板事件的选取很重要。以下为模板匹配法具体的流程:
(1) 模板的选取。强震过后发生的余震与主震具有相近的震源机制和传播路径, 所以波形互相关很好, 选取震相清晰且信噪比较高的事件作为模板事件。
(2) 互相关计算。将模板事件和连续的波形记录作滑动互相关, X(t)为连续波形记录,
| $ {\rm{CC}} = \frac{{\sum\nolimits_{{t_0}}^{{t_1}} {\left\{ {\left[ {X\left( t \right) - \bar X\left[ { * \left[ {Y\left( t \right) - \bar Y} \right]} \right.} \right.} \right\}} }}{{\sqrt {\sum\nolimits_{{t_0}}^{{t_1}} {{{\left[ {X\left( t \right) - \bar X} \right]}^2}} * \sum\nolimits_{{t_0}}^{{t_1}} {{{\left[ {Y\left( t \right) - \bar Y} \right]}^2}} } }} $ | (15) |
(3) 地震事件判别。将各个台站不同分量的互相关进行叠加平均得到平均互相关波形, 将其与设定好的阈值进行比对, 超过阈值的则认为是地震事件。
通过扫描在连续波形上识别出与模板事件波形相似的地震事件(图 4)。

|
图 4 模板匹配法识别震相示例(据李璐等(2017)) 蓝色波形为模板事件;数值为互相关系数值 |
随着模板匹配滤波方法的发展, 研究者对传统方法进行了不断的改进。Meng等(2012)将连续波形分成N个部分, 分别在不同线程下进行扫描, 极大地提高了计算速度。Peng等(2009)同时选取P波、S波附近垂直、水平分量的时间窗, 在互相关叠加时, 放大模板事件波形, 压制了不相关信号, 提高了信噪比。Harris(2006)、Barrett等(2014)都试图将需要匹配检测的模板波形多样化, 因而分别提出了子空间和经验子空间检测方法, 这使得模板匹配滤波方法更具有一般性。Zhang等(2015)提出了一种改进思路, 其被称为空间扫描算法, 即首先在叠加之前在模板事件附近划分三维网格, 每个网格都被认为是潜在事件位置, 基于潜在事件与模板事件的走时差进行校正, 校正方案如下
| $ \Delta t\left( {k,p} \right) = {\rm{d}}{D_k}\frac{{{\rm{d}}t}}{{{\rm{d}}D}}\left( {k,p,D,h} \right) + {\rm{d}}h\frac{{{\rm{d}}t}}{{{\rm{d}}h}}\left( {k,p,D,h} \right) $ | (16) |
其中, dDk为模板事件与潜在事件到台站k的相对震中距差异;dh为相对深度差异;
|
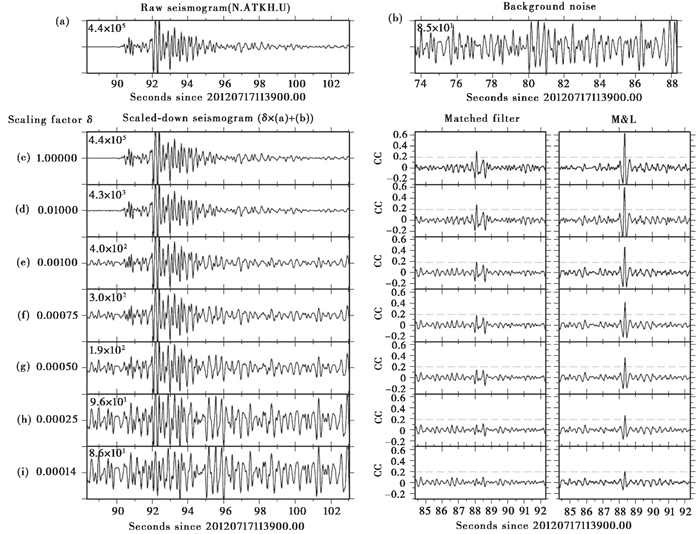
图 5 M & L方法与传统模板匹配法对比(据Zhang等(2015)) |
基于互相关的模板匹配技术计算效率较高, 对低信噪比的信号也有一定的适用性, 但其过于依赖模板的选取, 而模板的选取通常是人工下载拾取, 这使其在适用性上受到限制。Brown等(2008)在研究地颤动低频搜索问题中提出了一种基于波形自相关的检测技术, 该技术避免了选取先验模板信息。其思路如下:首先将每个台站每个分量地震序列按一定长度划分成一定数量的时间窗, 然后对这些时间窗作两两互相关, 并每个台站对应互相关波形叠加平均, 与设定好的阈值比对, 超过阈值的则视为候选事件;之后对同一台站的波形和这些候选事件作互相关, 得到各自的互相关系数, 再按照高低分组叠加来提高信噪比, 最后用该高信噪比模板进行模板匹配滤波技术补充搜索(Zhang et al, 2015)
| $ {a_{ij}} = \sum\limits_n {{\rm{C}}{{\rm{C}}_n}} = u\left( {{t_i}} \right) \times u\left( {{t_j}} \right) $ | (17) |
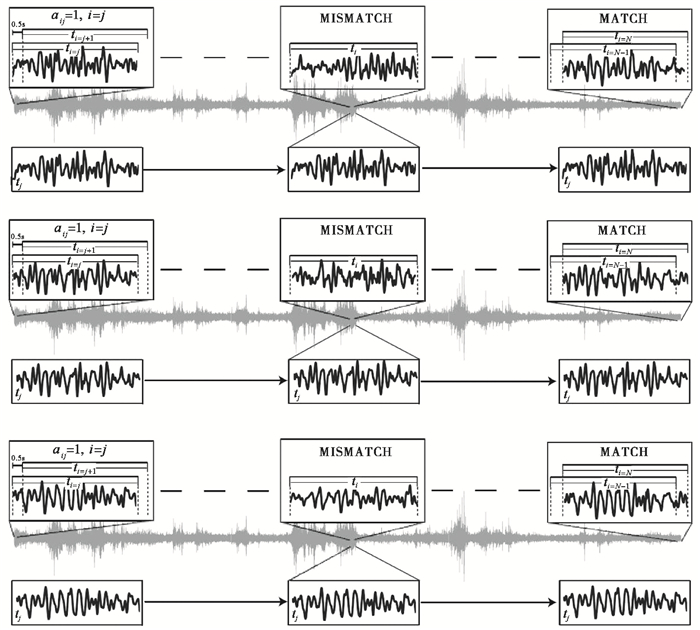
其中, n为台站号;CC为互相关值;u为时窗ti、tj下的地动位移。图 6为波形自相关方法原理图。
|
图 6 波形自相关方法原理图(据Brown等(2008)) |
基于波形自相关的检测方法不仅与互相关运算一样对噪声有良好的压制作用, 而且摆脱了对模板的依赖性, 其不足之处在于计算量较大, 对于大数据并不适用, 因而出现了改进算法FAST(fingerprint and similarity thresholding)。
FAST算法思想:2个信号在哈希函数转换前后的数据空间中都有很高的相似性, 或者变换前后相似性都不高。大体思路是对原始波形作频谱分析, 提取关键特征, 并将其压缩成二进制“指纹”, 然后采用LSH(locality-sensitive hashing)算法(即局部敏感哈希算法)将该指纹与数据库中的二进制“指纹”作快速相似性搜索成对, 最后生成地震事件检测列表(刘翰林等, 2017)。
1.5 对于S波拾取的偏振分析法对于S波的震相拾取, 由于受P波尾波信号的干扰, 长短时窗法识别并不可靠。Roberts等(1989)提出利用P波、S波偏振方向的不同来识别震相, Amoroso等(2011)对此作了深入研究, 具体方法如下:
第1步, 计算三分量地震记录的协方差矩阵, 最大特征值可以认为是P波偏振方向, 协方差矩阵表示如下
| $ {\bf{dec}}\left( \mathit{\boldsymbol{t}} \right) = \left\{ {\begin{array}{*{20}{c}} {{\mathop{\rm cov}} \left( {{\rm{N}},{\rm{N}}} \right)}&{{\mathop{\rm cov}} \left( {{\rm{N}},{\rm{E}}} \right)}&{{\mathop{\rm cov}} \left( {{\rm{N}},{\rm{Z}}} \right)}\\ {{\mathop{\rm cov}} \left( {{\rm{E}},{\rm{N}}} \right)}&{{\mathop{\rm cov}} \left( {{\rm{E}},{\rm{E}}} \right)}&{{\mathop{\rm cov}} \left( {{\rm{E}},{\rm{Z}}} \right)}\\ {{\mathop{\rm cov}} \left( {{\rm{Z}},{\rm{N}}} \right)}&{{\mathop{\rm cov}} \left( {{\rm{Z}},{\rm{E}}} \right)}&{{\mathop{\rm cov}} \left( {{\rm{Z}},{\rm{Z}}} \right)} \end{array}} \right\} $ | (18) |
其中, N、E、Z分别为北向、东向、垂向分量;cov为2个分量协方差。
第2步, 将方位坐标系旋转至偏振坐标系, 偏振三坐标轴分别记作L、Q、T, 分别表示P波震动方向、Sv波振动方向、Sh波振动方向, 用ψ表示射线入射角, β表示直达P波反方位角, 则有
| $ \left[ {\begin{array}{*{20}{c}} L\\ Q\\ T \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos \phi }&{ - \sin \phi \sin \beta }&{ - \sin \phi \cos \beta }\\ {\sin \phi }&{\sin \phi \sin \beta }&{\cos \phi \cos \beta }\\ 0&{ - \cos \beta }&{\sin \phi } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\rm{Z}}\\ {\rm{E}}\\ {\rm{N}} \end{array}} \right] $ | (19) |
第3步, 计算偏振函数, 取L、Q、T三分量协方差矩阵3个特征值λ1、λ2、λ3, 偏振函数表示如下
| $ p\left( t \right) = \frac{{{{\left( {{\lambda _1} - {\lambda _2}} \right)}^2} + {{\left( {{\lambda _1} - {\lambda _3}} \right)}^2} + {{\left( {{\lambda _2} - {\lambda _3}} \right)}^2}}}{{2\left( {{\lambda _1} + {\lambda _2} + {\lambda _3}} \right)}} $ | (20) |
当偏振函数取最大值时, 即为S波震相到时。Cichowicz(1993)提出联合偏斜度、偏振函数、能量比3个因素进行S波信号检测。Amoroso等(2011)用加权因子对实际值和观测值进行应用对比, 效果显著。Wang等(2017)对汶川8.0级地震P波、S波的拾取效果作了对比, 研究发现P波、S波的检出率分别为91%、85%, P波优于S波, 认为这是因为P波是具有比S波路径特征更简单的压缩波, 而S波的产生和传播相对复杂, 会在一定程度上受传播路径的影响。
1.6 人工智能方法神经网络最早由心理学家和神经学家创立, 发展至今已成为一种非线性建模识别方法, 相比于其他方法, 它有很多显著的优点, 如识别精度极高、非线性品质良好、学习方式灵活而有效、模型结构层次分明、存储结构呈完全分布式等, 基于这些特点, 神经网络被广泛应用于信号处理、模式识别及非线性优化等领域, 并显示出了巨大潜力(王金峰, 2006)。1986年Rumelhart等(1986)提出了经典的BP(error back propagation)算法, 将神经网络分为输入层、隐含层、输出层等3部分, 隐含层通常不止1层。相邻2层节点完备连接(即以上一层输出作为输入), 同一层内无连接, 跨层无连接, 每个连接都有1个权重。工作过程分为2个阶段, 第1个阶段为学习过程, 在这个过程中调整与连接相关联的权重, 使输出满足精度要求以达到学习的目的;然后进入第2个阶段, 利用学习好的神经网络进行工作, 输入地震数据, 输出识别结果。
经典的BP算法中使用最速下降法达到收敛结果, 但其具有一定的局限性, 比如容易局部收敛, 无法达到全局最优。另外, 经典BP算法的学习率为固定值, 始终保持不变, 这就显得不够灵活。如果学习率选的较高, 虽然收敛速度较快, 但同时也会发生振荡, 导致不能收敛到期望值;而如果学习率选的太低, 虽然可以保证收敛, 但收敛速度又太慢。王金峰等(2006)提出了基于梯度的学习效率自适应、基于误差的学习速率自适应等算法, 提高了学习效率。宋建国等(2018)提出了级联(cascade-correlation)相关算法, 该方法可以扩展网络拓扑结构以学习新样本, 并自行确定网络结构, 提高了收敛速度。
Perol等(2018)阐述了Conv Net Quake算法应用于地震事件检测定位的理论, 其算法的核心是由8个卷积层(z1~z8)组成的前馈系统和1个完全连接层z来输出, 所有层包含多个通道, 由二维张量表示。8个卷积层的每个通道由前一层与1个线性一维滤波器卷积得到, 其表示为
| $ Z_{c,t}^i = \sigma \left( {b_c^i + \sum\limits_{c' = 1}^{{C_i}} {\sum\limits_{t' = 1}^3 {Z_{c',st + t' - 1}^{i - 1} \cdot W_{cc't'}^i} } } \right) $ | (21) |
其中, σ为ReLU非线性激励函数;c、c′为输出与输入通道;t、t′为时间;Ci为第i层的通道数。与标准卷积的不同在于, 步幅s=2即以2个样本的增量滑动(而非1)。因而, 每层之后沿时间轴向下采样2个单位的数据, 8层之后将4×32的张量Z8矢量化为128个元素的矢量Z8, 之后通过1个线性完全连接层处理得到分类值zc
| $ {z_c} = \sum\limits_{c' = 1}^{128} {\bar Z_{c'}^8 \cdot W_{cc'}^9 + b_c^9} $ | (22) |
W为权重系数;b为修正值。通过此线性完全连接层把各种地震信号与分类值联系起来, 特定分类值输出代表地震事件, 由此便可拾取地震事件。表 1为Conv Net Quake算法的人工智能方法与FAST、Autocorrelation算法的对比。由表 1可见, 前者的运算速度比Autocorrelation快13500倍, 比FAST快48倍;而其可靠度可与Autocorrelation相媲美, 都要优于FAST算法, 说明其有很强的实用性。
| 表 1 Conv Net Quake算法与FAST、Autocorrelation算法结果对比(据Perol等(2018)) |
FP(filter picking)算法是Lomax等(2012)开发的一种用于实时地震监测和地震早期预警的算法。该算法可连续、实时、稳定地处理宽带信号, 并避免在大地震中的过度拾取。下面介绍其原理。
首先, 对原始的离散信号进行一阶差分
| $ y'\left( i \right) = y\left( i \right) - y\left( {i - 1} \right) $ | (23) |
然后进行滤波, 先是2个单极高通滤波器滤波, HP(high pass)代表高通滤波
| $ Y_n^{{\rm{H}}{{\rm{P}}_1}}\left( i \right) = C_n^{{\rm{HP}}}\left[ {Y_n^{{\rm{H}}{{\rm{P}}_1}}\left( {i - 1} \right) + y'\left( i \right) - y'\left( {i - 1} \right)} \right] $ | (24) |
| $ Y_n^{{\rm{H}}{{\rm{P}}_2}}\left( i \right) = C_n^{{\rm{HP}}}\left[ {Y_n^{{\rm{H}}{{\rm{P}}_2}}\left( {i - 1} \right) + {Y^{{\rm{H}}{{\rm{P}}_2}}}\left( i \right) - {Y^{{\rm{H}}{{\rm{P}}_2}}}\left( {i - 1} \right)} \right] $ | (25) |
随后单极低通滤波器滤波, LP(low pass)代表低通滤波
| $ Y_n^{{\rm{LP}}}\left( i \right) = Y_n^{{\rm{LP}}}\left( {i - 1} \right) + C_n^{{\rm{LP}}}\left[ {{Y^{{\rm{H}}{{\rm{P}}_2}}}\left( i \right) - {Y^{{\rm{H}}{{\rm{P}}_2}}}\left( {i - 1} \right)} \right] $ | (26) |
其中, 滤波器CnHP=ωn/(ωn+ΔT)、CnLP=ΔT/(ωn+ΔT);拐角周期Tn=2nΔT;y′(0)、YnHP1(0)、YnHP2(0)初始化为0;n由N决定, 其满足2N-1 ΔT大于最大主周期的最小值, 且取整数。由此可得到1组具有不同中心周期且恰好在Tn之下的带通时间序列。
特征函数定义为
| $ F_n^C\left( i \right) = \frac{{{E_n}\left( i \right) - < {E_n} > \left( {i - 1} \right)}}{{ < \sigma \left( {{E_n}} \right) > \left( {i - 1} \right)}} $ | (27) |
| $ {E_n}\left( i \right) = Y_n^{\rm{2}}\left( i \right) $ | (28) |
其中, σ为标准差, 尖括号表示时间上均值。设置阈值S1、S2, 当FnC(i)大于S1时, 记录触发时间ttrig, 此时最高频频带定义为触发带, 并给出时间窗Tup, 时间由ttrig至ttrip + Tup, 如果FnC(i)之和
FP算法是对离散时间序列进行操作的, 其可以运用少量没有进行预处理的数据, 甚至无需滤波和去平均, 而且, FP算法中只有基本的算术运算(即平方根等而没有指数、对数或变换算法等), 因此运算效率较高。
1.8 全波形叠加方法Grigoli等(2018)提出的全波形叠加方法以整个波形作为输入数据, 利用不同台站记录地震波形的相关性进行事件的识别和定位, 类似于地震学中的偏移技术。值得一提的是, 此方法在识别之前对每个台站的数据进行区域归一化, 具体如下
| $ F_i^{{\rm{P}}\left| {\rm{S}} \right.}\left( t \right) = \frac{{f_i^{{\rm{P}}\left| {\rm{S}} \right.}\left( t \right)}}{{\int_{{T_\alpha }}^{{T_\omega }} {f_i^{{\rm{P}}\left| {\rm{S}} \right.}\left( \theta \right){\rm{d}}\theta } }},{T_\alpha } \le t \le {T_\beta } $ | (29) |
| $ {T_\omega } = {T_\beta } + \mathop {\max }\limits_{i,x} \left[ {\tau _i^{\rm{S}}\left( x \right) - \tau _i^{\rm{P}}\left( x \right)} \right] $ | (30) |
其中, Tα、Tβ为时窗起止点;Tω作为缓冲窗口以弥补处理波形之间的间隙;i为台站名;fiP|S(t)为P/S波叠加函数;τiP|S(x)为P/S波相对整个系统的初至P波的相对走时。区域归一化可视为对每个台站的贡献的一种加权, 在压制大值的同时定性保留其相对其他值的大小, 它可以减弱尖脉冲和由于台站与震源太近对叠加波形的影响;然后, 将区域归一化后的P/S波叠加函数作为输入, 在一定时间窗内计算相关函数
| $ {C^{{\rm{P}}\left| {\rm{S}} \right.}}\left( {x,t} \right) = \sum\limits_i^n {\int_{{T_\alpha }}^{{T_\omega }} {F_i^{{\rm{P}}\left| {\rm{S}} \right.}\left( \theta \right)\delta \left[ {t + \tau _i^{{\rm{P}}\left| {\rm{S}} \right.}\left( x \right) - \theta } \right]{\rm{d}}\theta } } = \sum\limits_i^n {F_i^{{\rm{P}}\left| {\rm{S}} \right.}\left[ {t + \tau _i^{{\rm{P}}\left| {\rm{S}} \right.}\left( x \right)} \right]} $ | (31) |
其中, δ为狄拉克函数, 此时式(31)为空间和时间的函数, 下面通过提取每个时间t上的空间最大值获得时间相关函数
| $ C\left( t \right) = \mathop {\max }\limits_x \left[ {C\left( {x,t} \right)} \right] $ | (32) |
在搜索空间x下计算体积V下的平均相关函数
| $ \left\langle {C\left( t \right)} \right\rangle = \frac{1}{V}\int_V {C\left( {x,t} \right){\rm{d}}V} $ | (33) |
预设阈值H1、H2, 如果在某个时刻te满足以下条件, 则判别为地震事件
| $ C\left( {{t_{\rm{e}}}} \right) > {H_1};\;\;\;\;\;\frac{{C\left( {{t_{\rm{e}}}} \right)}}{{\left\langle {C\left( {{t_{\rm{e}}}} \right)} \right\rangle }} > {H_2} $ | (34) |
双阈值的操作用以减少错误判定事件的发生。这种基于波形相关方法的初衷是同步实现事件检测和定位, 事实上, 仅在拾取事件上就有不错的效果, 尤其在噪声较大的环境下, 效果更为显著。然而, 其局限性在于当台站布设较广而稀疏时, 需要扫描大片的区域, 计算量爆炸增长, 不适合实时监测与定位。
1.9 二次方自回归模型何先龙等(2016)采用一种二次方自回归模型对初至附近能量变化率曲线进行二次方自回归处理, 精确拾取了P、S波初至。首先, 他们将三分量离散的地震信号表示为能量变化率序列
| $ {E_i} = {\left( {{x_{i + 1}} - {x_i}} \right)^2}/\Delta t $ | (35) |
其中, xi为地震信号;Δt为样本的时间间隔, 对式(35)的能量变化率序列应用传统的长短时窗方法进行粗略拾取, 得到大致的到时区间, 然后, 基于二次方自回归模型法精确拾取震相。假设理想的二次方自回归模型方程为
| $ {c_i} = \omega + gi + f{i^2} $ | (36) |
其中, 未知参数为ω、g、f, 通过下式近似求解这3个未知数, 得出其近似序列c′ i(3个未知数为其系数)
| $ {u_i} = \frac{{\sum\limits_{j = i + 1}^{2s} {{q_j}} }}{{2s - i - 1}} $ | (37) |
| $ {a_i} = \frac{{\sum\limits_{j = i + 1}^{2s} {{{\left( {{q_j} - {u_i}} \right)}^2}} }}{{2s - i - 1}} $ | (38) |
| $ {d_i} = \frac{{\sum\limits_{j = 0}^{i + 1} {{q_j}} }}{{i + 1}} $ | (39) |
| $ {b_i} = \frac{{\sum\limits_{j = 0}^{i + 1} {{{\left( {{q_j} - {d_i}} \right)}^2}} }}{{i + 1}} $ | (40) |
| $ {{c'}_i} = \left[ {\left( {2s - i - 1} \right)\lg {a_i}} \right] \times \left[ {\left( {i + 1} \right)\lg {b_i}} \right] $ | (41) |
其中, 2s为序列长度;i为序数。由最小二乘法求解系数ω、g、f, 将其代入ci表达式(式(36)), 使ci为最大值时对应的i时刻即为精确到时。表 2为何先龙等(2016)在汶川8.0级地震研究中将二次方自回归模型方法与传统的长短窗法、赤池准则法进行比较得到的结果。由表 2可见, 虽然在计算效率上稍逊色, 但二次方自回归模型方法对地震事件检测的精度与准确率较高, 不失为一种优秀的方法。
| 表 2 二次方自回归模型拾取与经典方法对比表(据何先龙等(2016)) |
相对于早期人工拾取地震事件的低效率、低精度, 20世纪以来的各种自动拾取方法为地震学研究的发展做出了巨大贡献。Tamaribuchi等(2016)在对2016年7.1级熊本地震的研究中对自动拾取和人工拾取作了对比(图 1), 其对微地震拾取数量是人工拾取的14倍, 不仅在速度上有强大优势, 而且数量上更远优越于人工拾取。
震相自动拾取的每种方法各有优劣, 基于长短时窗一类的方法计算简单, 速度快, 不依赖先验的模板事件信息, 但是在面对低信噪比的数据记录时效果不佳, 阈值的设定很难, 阈值过大可能导致漏检, 过小可能导致误检。基于波形互相关模板匹配的方法能有效压制背景噪声, 在处理低信噪比的信号时有优势, 但对模板的选取过于依赖, 在地下结构十分复杂的情况下模板选取不具代表性, 选取困难。基于波形自相关的搜索方法较好地解决了上述2个问题, 但其计算量过大, 易导致实际应用效果不佳, 即使引入了数据挖掘中的优化算法, 依然有着庞大计算量。神经网络应用于地震震相拾取对噪声具有较高的承受能力, 这使其占有比较重要的地位, 在Perol等(2018)的研究中拾取准确率近100%, 准确率得以保障。但是, 该方法需要较长的训练时间, 而且需要大量依靠经验的参数, 这使得其在可解释性方面较差。近几年发展起来的多频率震相识别、全波形叠加、二次方自回归模型等方法都从现代的视角分析问题, 尽管有一些问题(如运算速度等)有待解决, 但在实际应用中都可以发挥一定的作用, 如二次方自回归模型(何先龙等, 2016)用于拾取汶川8.0级地震震相时已达到P波误差大于0.1s的事件数仅为1个, S波误差大于0.1s的仅为3个, 比传统的长短时窗法等已有了很大的突破。
一种震相自动拾取方法很难同时兼顾精度和效率, 因此, 合理运用每种方法的优势, 规避劣势可以在提高震相识别效率的同时又提高精度。比如, 可以将长短时窗法与AIC方法结合起来, 先用前者粗略拾取到时, 然后设置时间窗用后者使到时更精确。总之, 可以通过联合运用各种方法来综合识别震相, 从而得到满意的效果。
高淑芳、李山有、武东坡等, 2008, 一种改进的STA/LTA震相自动识别方法, 世界地震工程, 24(2): 37-41. |
何先龙、佘天莉、高峰, 2016, 一种地震P波和S波初至时间自动拾取的新方法, 地球物理学报, 59(7): 2519-2527. |
何小波、周蕙兰, 2005, 利用定尺度小波变换比方法测量远震极远震P和PKIKP震相到时, 地震学报, 27(4): 385-393. DOI:10.3321/j.issn:0253-3782.2005.04.004 |
蒋策, 2017, 流动台阵地震检测与震相自动拾取研究, 1~48, 硕士学位论文, 北京: 中国地震局地球物理研究所. http://cdmd.cnki.com.cn/Article/CDMD-85401-1017112547.htm
|
李璐、王宝善、侯金欣, 2017, 模板匹配滤波技术在地震数据处理中的应用, 中国地震, 33(1): 14-22. DOI:10.3969/j.issn.1001-4683.2017.01.002 |
刘翰林、吴庆举, 2017, 地震自动识别及震相自动拾取方法研究进展, 地球物理学进展, 32(3): 1000-1007. |
刘希强、周彦文、曲均浩等, 2009, 应用单台垂向记录进行区域地震事件实时检测和直达P波初动自动识别, 地震学报, 31(3): 260-271. DOI:10.3321/j.issn:0253-3782.2009.03.003 |
吕鹏、丁志峰、朱露培, 2011, 结合波形互相关的双差定位方法在2008年汶川地震余震序列中的应用, 地震学报, 33(4): 407-419. DOI:10.3969/j.issn.0253-3782.2011.04.001 |
马强、金星、李山有等, 2013, 用于地震预警的P波震相到时自动拾取, 地球物理学报, 56(7): 2313-2321. |
裴正林、余钦范, 1999, 基于小波变换和BP神经网络的地震波初至拾取方法, 勘察科学技术, (4): 61-64. DOI:10.3969/j.issn.1001-3946.1999.04.015 |
沈统、庹先国、李怀良等, 2017, 利用偏振约束对最小信息准则方法自动拾取微震初至的改进, 科学技术与工程, 17(23): 26-30. DOI:10.3969/j.issn.1671-1815.2017.23.005 |
宋建国、李赋真、徐维秀等, 2018, 改进的神经网络级联相关算法及其在初至拾取中的应用, 石油地球物理勘探, 53(1): 8-16. |
谭毅培、邓莉、曹井泉等, 2016, 2015年河北滦县震群发震机理分析, 地球物理学报, 59(11): 4113-4125. DOI:10.6038/cjg20161115 |
王金峰、罗省贤, 2006, BP神经网络的改进及其在初至波拾取中的应用, 物探化探计算技术, 28(1): 14-17. DOI:10.3969/j.issn.1001-1749.2006.01.005 |
余建华、李丹丹、韩国栋, 2011, 特征函数响应特性分析及STA/LTA方法的改进, 国外电子测量技术, 30(7): 17-19. DOI:10.3969/j.issn.1002-8978.2011.07.004 |
赵大鹏、刘希强、刘尧兴等, 2013, 高阶统计量及AIC方法在区域地震事件和直达P波初动识别中的应用, 地震地磁观测与研究, 34(5/6): 61-69. |
Allen R V, 1978, Automatic earthquake recognition and timing from single traces, Bull Seismol Soc Am, 68(5): 1521-1532. |
Amoroso O, Maercklin N, Zollo A, 2011, S-wave identification by polarization filtering and waveform coherence analysis, In: Proceedings of EGU General Assembly, Vienna: European Geosciences Union. https://www.researchgate.net/publication/210212283_S-wave_identification_by_polarization_filtering_and_waveform_coherence_analysis
|
Barrett S A, Beroza G C, 2014, An empirical approach to subspace detection, Seismol Res Lett, 85(3): 594-600. DOI:10.1785/0220130152 |
Brown J R, Beroza G C, Shelly D R, 2008, An autocorrelation method to detect low frequency earthquakes within tremor, Geophys Res Lett, 35(16): L16305. DOI:10.1029/2008GL034560 |
Cichowicz A, 1993, An automatic S-phase picker, Bull Seismol Soc Am, 83(1): 180-189. |
Dai H C, MacBeth C, 1997, The application of back-propagation neural network to automatic picking seismic arrivals from single-component recordings, J Geophys Res, 102(B7): 15105-15113. DOI:10.1029/97JB00625 |
Gibbons S J, Ringdal F, 2006, The detection of low magnitude seismic events using array-based waveform correlation, Geophys J Int, 165(1): 149-166. DOI:10.1111/gji.2006.165.issue-1 |
Grigoli F, Scarabello L, Böse M, et al, 2018, Pick-and waveform-based techniques for real-time detection of induced seismicity, Geophys J Int, 213(2): 868-884. DOI:10.1093/gji/ggy019 |
Harris D B, 2006, Subspace detectors:theory, CA: Lawrence Livermore National Laboratory.
|
Kato A, Nakagawa S, 2014, Multiple slow-slip events during a foreshock sequence of the 2014 Iquique, Chile MW8.1 earthquake, Geophys Res Lett, 41(15): 5420-5427. DOI:10.1002/2014GL061138 |
Lomax A, Satriano C, Vassallo M, 2012, Automatic picker developments and optimization:filterpicker-a robust, broadband picker for real-time seismic monitoring and earthquake early warning, Seismol Res Lett, 83(3): 531-540. DOI:10.1785/gssrl.83.3.531 |
Meng X F, Yu X, Peng Z G, et al, 2012, Detecting earthquakes around Salton Sea following the 2010 MW7.2 El Mayor-Cucapah earthquake using GPU parallel computing, Proc Comput Sci, 9: 937-946. DOI:10.1016/j.procs.2012.04.100 |
Peng Z G, Zhao P, 2009, Migration of early aftershocks following the 2004 Parkfield earthquake, Nat Geosci, 2(12): 877-881. DOI:10.1038/ngeo697 |
Perol T, Gharbi M, Denolle M, 2018, Convolutional neural network for earthquake detection and location, Sci Adv, 4(2): e1700578. DOI:10.1126/sciadv.1700578 |
Roberts R G, Christoffersson A, Cassidy F, 1989, Real-time event detection, phase identification and source location estimation using single station three-component seismic data, Geophys J Int, 97(3): 471-480. DOI:10.1111/gji.1989.97.issue-3 |
Rumelhart D E, Hinton G E, Williams R J, 1986, Learning representations by back-propagating errors, Nature, 323(6088): 533-536. DOI:10.1038/323533a0 |
Schaff D P, Richards P G, 2004, Repeating seismic events in China, Science, 303(5661): 1176-1178. DOI:10.1126/science.1093422 |
Sleeman R, van Eck T, 1999, Robust automatic P-phase picking:an on-line implementation in the analysis of broadband seismogram recordings, Phys Earth Planet Inter, 113(1/2/3/4): 265-275. |
Stevenson P R, 1976, Microearthquakes at Flathead Lake, Montana:a study using automatic earthquake processing, Bull Seismol Soc Am, 66(1): 61-80. |
Tamaribuchi K, Moriwaki K, Ueno H, et al, 2016, Automatic hypocenter determination for the seismological bulletin of Japan using Bayesian estimation, Earthquake Times, 79: 1-13. |
Wang Z J, Zhao B M, 2017, Automatic event detection and picking of P, S seismic phases for earthquake early warning and application for the 2008 Wenchuan earthquake, Soil Dyn Earthquake Eng, 97: 172-181. DOI:10.1016/j.soildyn.2017.03.017 |
Yoon C E, O'Reilly O, Bergen K J, et al, 2015, Earthquake detection through computationally efficient similarity search, Sci Adv, 1(11): e1501057. DOI:10.1126/sciadv.1501057 |
Zhang M, Wen L X, 2015, An effective method for small event detection:match and locate(M & L), Geophys J Int, 200(3): 1523-1537. DOI:10.1093/gji/ggu466 |
 2018, Vol. 34
2018, Vol. 34



