地震震级是表征地震强弱的量度,是地震三要素的基本参数之一。第1个震级标度是李克特根据古登堡与达清夫的建议在1935年提出的。Richter(1958)在研究美国南加州的地震时引入的地方性震级标度ML,曾被认为“如果没有进一步的证据,不能应用于加利福尼亚以外的地区”。
20世纪50年代中期,李善邦先生结合我国常用的62型(短周期地震仪)和基式(SK,中长周期地震仪)仪器特性,将Richter提出的震级标度变换为适用于我国的量规函数R1和R2,并在全国范围内使用。严尊国等(1995)在收集了东北、华北、华东、华南、西南和西北等地区地动位移资料后,利用震级残差统计分析和地方性地震最大震相平均衰减形态来研究我国东部和西部的地方性震级量规函数,并确定了使用范围,从而进一步完善了ML震级测定方法。随着全国台网数字化改造的完成,各台网之间的数据实现了共享,在大震速报和地震编目等日常工作中也逐渐发现不同区域台网之间对于同一地方性地震事件所测震级有明显差别,同一地震事件,不同震中距台站所测震级差可达2.0级。与此同时,河北、甘肃和山西等区域台网利用近几年积累的丰富的数字地震资料研究了本区域的量规函数(赵明淳等,2005;陈继锋等,2013;董春丽等,2007),提高了其测定震级的精度。
新疆地处印度板块向欧亚板块俯冲的前缘地带,是中国大陆主要的内陆地震活动区,地震灾害频发,每年记录到大小地震2万余次。新疆测震台网有关本区域量规函数的研究还停留在由高国英等(1987)结合模拟测震数据利用统计方法得到的结果。本文旨在利用新疆测震台网近几年积累的数字地震资料,遵循我国地壳地区性特征的ML震级量规函数的继承性、区域性、实用性原则(严尊国等,1992),依据区域台网地理范围的行政分区边界,运用震级残差统计和最大地动位移衰减特性2种方法,研究新疆台网地方性震级量规函数,以期为提高新疆测震台网测定地方性震级精度提供参考。
1 研究方法本文采用震级残差统计和最大地动位移衰减特性2种方法,分别计算新疆台网地方性震级量规函数。震级残差统计实际上采用的是均匀震级系统的思想,是一种自我完善的方法,是对现阶段使用的量规函数的一种修正和完善。利用最大地动位移衰减特性研究地方性震级量规函数是建立在Richter关于零级地震的定义基础上,两者都非另立系统。
1.1 震级残差统计方法我国的地方性震级ML标度系统始建于1959年,建立的ML测定公式为
| $ {M_{\rm{L}}} = \lg \left({\frac{{{A_{\rm{N}}} + {A_{\rm{E}}}}}{2}} \right) + R\left(\mathit{\Delta } \right) $ | (1) |
式中,AN、AE分别为NS、EW方向记录最大地动位移(无须严格追踪到同一时刻,单位以μm计);R(Δ)为适合各地区实际情况的量规函数。
1971年,针对我国常用的短周期和中长周期地震仪建立了地方性震级量规函数R1(Δ)和R2(Δ),进一步完善了ML震级测定方法。1978年将R1(Δ)列入《地震台站观测规范》(试行)。多年来的实际观测和研究表明,R1(Δ)和R2(Δ)在反映我国地壳的地区性特征方面还存在一些问题。震级残差统计方法遵循了地方性震级测定的继承性,计算出的地方性震级量规函数是对现有的量规函数的一种修正。
台网震级Mi,即对第j个台站,按照地方性震级公式求得Mij,然后对第i个地震所有记录到的子台按照下式求震级平均值和标准偏差
| $ {M_i} = \frac{1}{N}\sum\limits_{j = 1}^N {{M_{ij}}} $ | (2) |
| $ {\delta _i} = \sqrt {\frac{{\sum\nolimits_{j = 1}^N {{{\left({{M_{ij}} - {M_i}} \right)}^2}} }}{{N - 1}}} $ | (3) |
对于第i个地震,第j个子台的震级偏差采用下式计算
| $ \mathit{\Delta }{M_{ij}} = {M_{ij}} - {M_j} $ | (4) |
| $ \mathit{\Delta }{M_i} = \frac{1}{N}\sum\limits_{j = 1}^N {\left({{M_{ij}} - {M_i}} \right)} $ | (5) |
| $ \overline {\mathit{\Delta }{M_k}} = \frac{1}{N}\sum\nolimits_{j = 1}^N {\mathit{\Delta }{M_j}} $ | (6) |
式中,k为间隔序数;N为间隔范围内震级偏差样本数(郭履灿等,1984;陈运泰等,2004)。
1.2 最大地动位移衰减特性方法1935年,Richter使用美国南加州的地震资料验证了“用同样的仪器在相同的震中距离上记录两次地震所得的最大振幅之比是一个与震中距无关的常数”,同时定义了零级地震为“在震中距为100km时,标准短周期扭转型地震仪(T=0.8s,放大率V=2800,阻尼常数D=0.8)所测最大地震波振幅为1μm”(林仙坎,2006)。利用最大地动位移衰减特征研究地方性震级量规函数就是建立在上述理论基础上。
通过假定lgA-Δ的关系可以表示为
| $ \lg {A_i} = {b_0} + {b_1}{\mathit{\Delta }_i} + \frac{{{b_2}}}{{{\mathit{\Delta }_i}}} + {b_3}\mathit{\Delta }_i^2 + {b_4}\mathit{\Delta }_i^2 + {b_5}\sqrt {{\mathit{\Delta }_i}} + \frac{{{b_6}}}{{\sqrt {{\mathit{\Delta }_i}} }} + {b_7}\lg {\mathit{\Delta }_i} + {b_8}{{\rm{e}}^{{\mathit{\Delta }_i}}} $ | (7) |
式中,i=1~N;A为最大地动位移;Δ为震中距。通过“有进有出”的多元回归分析方法找出lgA-Δ的关系式(中国科学院计算中心概率统计组,1979),从而拟合出最大地动位移衰减关系。利用零级地震的定义,进而求出地方性震级量规函数。
2 资料选取与处理结果随着“十五”数字化地震观测网络项目和中国地震背景场探测项目的建设,新疆测震台网基本建成了一个覆盖全疆、拥有84个数字测震台站的地震观测网络。本文采用了新疆数字地震台网2009年1月~2014年12月所记录的地震事件。依托省级台网之间数据共享,即新疆测震台网与甘肃、西藏和青海相邻台网共享原始地震记录,使新疆测震台网部分记录事件由网外变为网内。同时对所选的地震事件逐条都进行仔细地综合分析,地震定位采用由广东省地震局开发的MSDP交互处理软件,测定震源基本参数时采用单纯型法定位程序进行定位,并利用3400走时表求出发震时刻。
2.1 震级残差统计方法为了使被研究事件尽可能地覆盖研究区域且综合考虑近台和远台的权重比,选取了2009年1月~2014年12月间2.0≤ML≤5.4的地震事件作为研究对象,同时要求每个地震事件至少有5个观测台站记录,且震源深度小于50km,最终共得到16269个地震样本(图 1),震中距范围取0~800km。在测定震级时,将速度记录仿真成位移记录后(消除周期对结果的影响),量取两水平向最大振幅,然后根据式(1)求出各子台震级值,继而求出多台震级平均值。

|
图 1 震级残差统计方法选用的地震震中分布 WMQ:乌鲁木齐台; KSH:喀什台; HTA:和田台; WUS:乌苏台; WNQ:温泉台; FUY:富蕴台; BKO:巴里坤台:KMY:克拉玛依台; BCH:巴楚台; KOL:库尔勒台; XNY:新源台; KUC:库车台; YUT:于田台; QMO:且末台; RUQ:若羌台; BTS:北塔山台; HEF:和丰台; RGN:二宫台; GAZ:高崖子台; HTB:呼图壁台; LHG:硫磺沟台; LSG:柳树沟台; BLT:巴伦台台; STZ:石梯子台; TCH:天池台; WSU:乌苏台; WSC:乌什城台; JHE:精河台; MUL:木垒台; BAC:巴楚台; AHQ:阿合奇台; AKS:阿克苏台; ZSU:昭苏台; ALT:阿勒泰台; TAG:塔干台; HBH:哈巴河台; FUH:福海台; TAC:塔城台; QHE:清河台; SCH:石场台; ALS:阿拉山口台; XYD:下野地台; WCW:五彩湾台; SHZ:石河子台; CBC:察布查尔台:KMS:库米什台; YMS:雅满苏台; LTA:轮台台; HYS:火焰山台; ALR:阿拉尔台; BPM:八盘水磨台:WUQ:乌恰台;XKR:西克尔台; SMY:神木园台; ATS:阿图什台; YPH:岳普湖台; YJS:英吉沙台; YCH:叶城台; KSZ:喀什中继台; HTTZ:和田台阵台; DIK:迪坎尔台; DSZ:独山子台; JIG:吉根台; HLJ:哈拉峻台; SSH:鄯善台; YUM:裕民台; YWU:伊吾台; KNS:喀纳斯台; TAZ:塔中台; MIF:民丰台; SSL:三十里营房台; MGT:麦盖提台; KEP:柯坪台; SQHE:狮泉河台; GZE:改则台;SUH:双湖台; TTH:沱沱河台; GOM:格尔木台; WTM:乌图美仁台; DCD:大柴旦台; HTG:花土沟台; GCG:干柴沟台; LEH:冷湖台; DHT:敦煌台台; AXX:安西台;LYT:柳园台 |
对所选用的新疆数字地震台网84个子台所记录的179561个地震数据进行整理统计,按照式(2)、(4)计算得出单台震级与平均震级的偏差,并做统计分析,结果见图 2。由图 2可见,偏差值基本呈正态分布,集中度较高,在被分析的179561个单台震级中,偏差值(绝对值)在0.2以内的有106615次,占59.3%;0.3~0.5有60460次,占33.7%;0.6~0.8有11645次,占6.5%;大于0.9的841次,占0.5%。
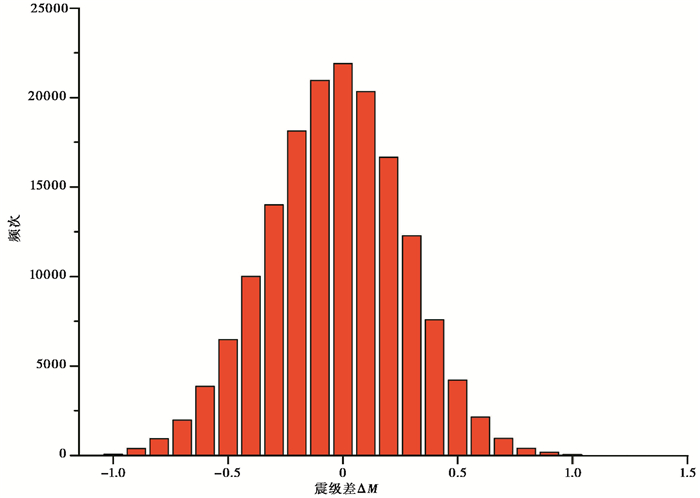
|
图 2 单台震级与平均震级偏差正态分布 |
采用式(3)~(5)得出各子台震级相对于台网震级偏差、平均偏差和标准偏差等,计算结果见表1。每个台站的平均偏差范围从-0.40~0.79,除了WCW(五彩湾)台偏差较大外,剩余台站都控制在±0.5的范围内。标准偏差值反映了震级偏差值的离散程度,其中WCW(五彩湾)和STZ(石梯子)2个台站的标准偏差较大,其余都在±0.5范围内,说明震级偏差离散程度较小。其中WCW台的台基类型为砂岩,砂岩对地震具有放大效应,计算出来的震级也偏大;而STZ台的台基为砾岩,由其场地条件计算出的场地响应值较大,对地震震级也起到放大作用(刘建明等,2014)。
为了研究单台震级随震中距的变化,利用式(6)将前述179561个单台震级偏差数据按照震中距由近到远排序,在0~800km范围内,以10km为间隔,分为80个间隔,求出每个间隔内其平均偏差值ΔMk。计算结果见图(3)。
从图 3可以看出,当震中距在0~150km以内时,单台震级与平均震级的偏差基本都超过了-0.18,在个别震中距段甚至接近-0.3,表明此震中距范围量规函数偏小。当震中距超过150km时,单台震级与平均震级的偏差基本都在± 0.1的范围内,震级偏差较小,取震级偏差的负值为校正值,对现有的量规函数进行校正,得出较正后的量规函数。
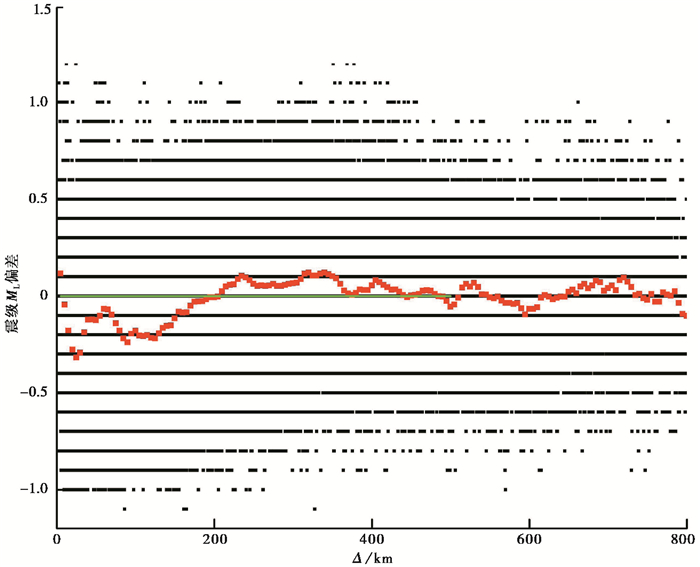
|
图 3 震级偏差值随震中距的分布 黑色点为单台震级偏差值;红色点为震级偏差平均值;绿线为零线 |
利用多元回归分析研究地方性震级量规函数时,选取的“母本”资料对量规函数的实用性和科学性有很大影响。黄玮琼等(1982)在研究最大地动位移的衰减规律时,提出震级选取应相差不大,如若选取的震级偏大,体波震级已不能反映地震的真实大小,地方性震级量规函数已失去意义;若选取的震级偏小,新疆区域面积大,会造成远台无法记录到地震,容易造成近台权重过大,而失去地方性震级量规函数的真实性。
为了使不同震中距范围内的观测资料尽可能地等权,在选取资料时,要求每个地震记录的台数不少于10个,且震源深度不能超过50km,同时每个台站记录的地震条目也不能低于10个。依据上述条件选取了2009~2014年746个ML3.6~4.5地震作为研究对象(图 4),用以研究新疆地区最大地动位移衰减特性,进而得出地方性震级量规函数。
|
图 4 最大地动位移衰减关系选用的地震震中分布 |
本研究所量取的最大地动位移都是由广东省地震局开发的MSDP经W·A仿真处理后得到的。根据每个地震定位的震中位置,由各台站的经纬度算出地震与台站的距离-震中距Δ,再对各台站记录的EW向和NS向最大地动位移值平均数取对数,这样就得到了lgA-Δ的数据对,共计算得到17011个这样的数据对。将17011个数据对按照震中距从0~800km的范围排序,由于数据较多,各台最大地动位移信息包含的物理意义也相差较大,若不经任何形式的预处理直接进行回归分析,会使回归效果不理想。预处理时按照每10km的间隔,从小到大顺序分割出一系列震中距段(i=1~80),把每一段中的lgAj-Δj(j=1~n,n为该震中距段lgA-Δ的数量)进行平均,得到lgAi-Δi(i=1~80)。采用式(7)对这80对数据进行“有进有出”的多元回归分析,回归分析过程中显著性水平为0.05,多元回归分析模型标准误差为0.07,回归模型成立。
拟合出来的最大地动位移衰减关系式为
| $ \lg A\text{=}2.55\text{-}0.05\sqrt{\mathit{\Delta }}\text{-}0.83\lg \mathit{\Delta },\ 0\le \mathit{\Delta }\le 800$ | (8) |
其中,常数项为震源信息项,与衰减特征无关。
根据李氏震级关于零级地震的定义,由lg2800=3.45,依据最大地动位移衰减关系式,得出地方性震级量规函数的表达式为
| $ R\left( \mathit{\Delta } \right)=3.45+0.05\left( \sqrt{\mathit{\Delta }}-10 \right)+0.83\left( \lg \mathit{\Delta }-2 \right),0\le \mathit{\Delta }\le 800 $ | (9) |
经前文的讨论, 可得出如下认识和结论:
(1) 由震级残差统计和最大地动位移衰减关系得出的地方性震级量规函数如图 5所示。
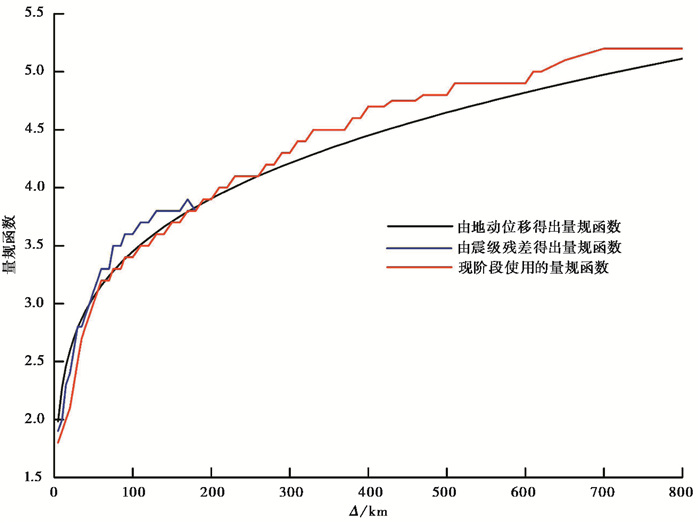
|
图 5 两种方法计算出的量规函数与现阶段使用的量规函数的对比 |
经分析图 5可知,现阶段使用的量规函数在震中距0~200km的范围内,地方性震级量规函数偏小,导致近台震级偏小,由震级的偏差值分布特征也可反映出在0~200km的范围内震级偏差皆小于平均震级;而由最大地动位移衰减关系得出的地方性震级量规函数在400~800km范围内比现阶段使用的量规函数和由震级残差得出量规函数都偏小;在200~800km范围内测算出来的震级值偏差值保持在±0.1的范围内,计算地方性震级时,应尽量选用此范围内的台站进行测算。
(2) 新疆测震台网拥有84个数字测震台站,再加上共享邻省的17个台站数据,能较好地覆盖全区域的地震活动,对于边境地区和塔里木盆地中部,由于台站分布偏向一侧,故可忽略此区域的震源辐射方位。此外,本文所选用的均为ML≥2.0地震,保证至少5个以上台站的观测资料对震中的围绕,基本消除了震源辐射方位的影响。
(3) 由震级残差统计得出的量规函数中仪器、方位等其他影响因素:通过对选用的新疆测震台网数字地震记录资料,对75个台站的数据进行分析,除了TCH、WCW、XKR、STZ和JIG这5个台的震级偏差较大外,有54个台站的震级偏差都在±0.2的范围内,占所有台数的72%。其中JIG台是临时台,台基条件为砂岩,且风化严重;WCW台在矿区当中,记录的地震事件常常受到干扰;对TCH、XKR和STZ台,由于这3个台计算出的场地响应值较大(刘建明等,2014),台基对地震波有放大作用,计算出的震级会普遍偏大。
(4) 分别由震级残差统计和地动位移衰减特性得出的量规函数之间有一定的差距,主要表现在所使用的方法的不同。震级残差统计方法得出的量规函数是在原有量规函数的基础上一种取平均的思想,而由地动位移衰减特性得出的量规函数是反映真实的地震波的衰减,但由地动位移计算量规函数需依赖于各台站精确的仪器响应。由于现阶段使用的台站地震仪器响应都存在一定的偏差,故在今后的研究中应两者结合对比,以便得出更加精确的新疆地区地方性震级量规函数。
致谢: 感谢刘瑞丰研究员对本文修改提出的宝贵意见。
陈继锋、尹欣欣、董宗明等, 2013, 甘肃地区近震震级的量规函数研究, 中国地震, 29(3): 328-334. |
陈运泰、刘瑞丰, 2004, 地震的震级, 地震地磁观测与研究, 25(6): 1-12. DOI:10.3969/j.issn.1003-3246.2004.06.001 |
董春丽、梁向军、陈冬焱, 2007, 山西数字地震台网单台测定近震震级偏差研究, 地震地磁观测与研究, 28(2): 42-46. |
高国英、艾尼瓦尔, 1987, 新疆地区量规函数、台站校正值的分析计算, 西北地震学报, 9(1): 103-107. |
郭履灿、赵凤竹、赵共玲等, 1984, 震级与震源参数测定, 北京: 中国科学技术出版社.
|
黄玮琼、金严、胡荣盛, 1982, 近震衰减特征的地区差异及近震震级的估算, 地震学报, 4(4): 338-348. |
林仙坎, 2006, 闽台地区近震震级ML量规函数研究, 中国地震, 22(3): 288-293. |
刘建明、李志海, 2014, 新疆北天山非弹性衰减、场地响应及其震源参数研究, 地震, 34(1): 79-85. |
严尊国、李普丽、薛军蓉, 1992, 中国近震震级量规函数研究, 中国地震, 8(4): 76-91. |
严尊国、李普丽、薛军蓉, 1995, 中国近震震级量规函数检验研究, 华南地震, 15(1): 2-11. |
赵明淳、毛国良、张从珍等, 2005, 河北遥测台网速报震级偏差与量规函数关系的研究, 地震地磁观测与研究, 26(5): 88-94. |
中国科学院计算中心概率统计组, 1979, 概率统计计算, 119. 北京: 科学出版社.
|
Richter C F, 1958, Elementary Seismology, San Francisco; W H Freeman, 1~768.
|
 2018, Vol. 34
2018, Vol. 34


