0 引言

近年来全球发生的多次8级以上巨大地震造成了严重的人员伤亡和财产损失。大震后短时间内余震活动频繁, 极易引起重大次生灾害。因此, 大地震余震活动研究、序列类型判定和强余震预测在抗震救灾、区域地震危险性评估等方面具有非常重要的意义(蒋海昆等, 2007a)。

由于全球布设较为完善的地震台网时间不长, 且大地震的复发周期较长, 因此, 有完整小震记录以来8级地震震例较少。人们对地震序列的研究主要集中在5级以上地震(蒋海昆等, 2007a、2007b；吴开统等, 1990；Wells et al, 1994；Chen et al, 2013、2016)。近年来, 学者们对全球大震序列进行了一定的研究。吕晓健等(2010)研究了全球大陆地区29次7.0~7.9级浅源地震中走滑型与非走滑型地震的强余震震级分布特征和时间分布特征。苏有锦等(2008)按照板内、板间地震及震源机制解类型研究了1975~2007年全球8级以上地震序列最大余震的震级分布特征, 以及5、6级余震频度与最大余震发生时间的特征, 讨论了震区背景地震活动水平与余震活动水平间的关系。苏有锦等(2014)研究了1975~2010年全球7级以上地震序列, 内容包括序列分类、余震频度、最大余震、余震区线性度与背景地震活动、最大余震间的关系等。人们通常将8级以上地震称为巨大地震。Mogi(1974)将7.8级以上地震也作为巨大地震, 研究了全球7.8级以上板间巨大地震的时空分布特征。梅世蓉等(1996)研究了我国大陆及邻区7.8级以上巨大地震前后地震活动图像特征。

余震序列参数可以反映序列的衰减特征和激发余震的能力, 不同的构造区域、序列类型、主震震源机制解类型、震源区局部构造应力水平和大地热流等地球物理特征都可以表现为序列参数的显著差异(Kagan et al, 2010)。对余震序列参数特别是早期参数特征(蒋海昆等, 2007a)的研究一直是地震学和地球物理学研究的热点问题。学者们应用“传染型余震序列(epidemic-type aftershock sequence, 简写为ETAS)”模型研究了不同区域地震序列参数, 得到了一些有意义的结果(Guo et al, 1997；Ogata, 1998；庄建仓等, 2000)。蒋海昆等(2007c)应用ETAS模型系统研究了我国大陆地区中强以上地震序列早期参数的平均统计特征, 讨论了b值、p值、a值随不同的区域、主震断层类型、序列类型的变化。蒋长胜等(2014)研究了2008年以来新疆于田地区3次强震序列的早期参数特征。

本文将系统研究1976~2016年全球M_W≥7.8浅源(震源深度小于70km)地震序列的统计特征, 内容包括地震序列类型划分、序列类型与主震震源破裂方式间关系、最大余震与主震的时间间隔及震级差、余震区规模与主震震级间关系等, 并应用ETAS模型计算序列参数。

1 地震目录完备震级讨论与地震序列的挑选原则

本文使用美国国家地震信息中心(NEIC)提供的全球地震目录(http://earthquake.usgs.gov)研究地震序列, 震源机制解数据来源于美国哈佛大学(http://www.globalcmt.org/CMTsearch.html)。美国国家地震信息中心(NEIC)1973年以来的全球地震目录使用了多个震级标度, 其中, 4~5级地震多为m_b震级, 6级以上主要为M_W、M_S震级, 而对于7.8级以上地震, 主要为M_W震级。本文对该目录所有地震震级统一采用M表示。

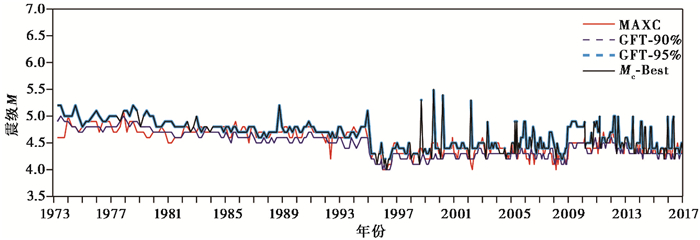
利用“最大曲率(MAXC)及拟合度分别为90%、95%的GFT”方法(Wiemer et al, 2002)计算1973~2017年全球地震目录的最小完备性震级, 其中, 95%GFT方法给出的结果优于90%GFT, 同时这2个方法的结果又优于最大曲率方法。依据择优原则, 给出最佳最小完备震级M_c-best(图 1)。由图 1可见, 1973~1994年最小完备震级为4.6~5.0级；1995~2012年为4.3~4.7级；2013~2016年为4.2~4.6级。

挑选地震序列的原则：以主震后1个月内形成的余震密集区为挑选区域, 挑选主震后3个月内的地震资料, 震级下限为M4.0。值得注意的是, 2004年12月26日苏门答腊9.1级地震后3个月(即2005年3月28日)又发生8.6级地震, 这2次地震的余震区不重合, 所以将其作为2个独立的地震序列；2006年11月15日千岛群岛8.3级地震后2个多月(即2007年1月13日)在其震中附近又发生8.1级地震, 这2次地震震中相距约100km, 余震区大致重合, 故将其作为1个序列进行处理；1987年11月30日阿拉斯加7.9级地震后3个月(即1988年3月6日), 在其震中南部约196km处又发生7.8级地震, 2次地震的余震区不重合, 故作为2个独立的地震序列(附表 1)。

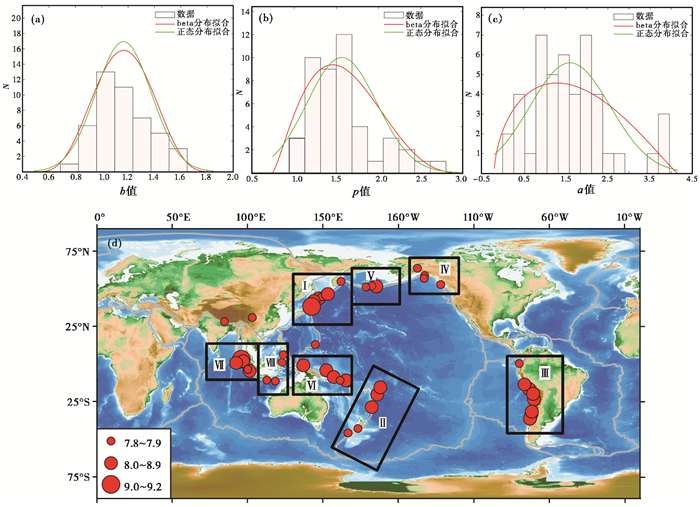
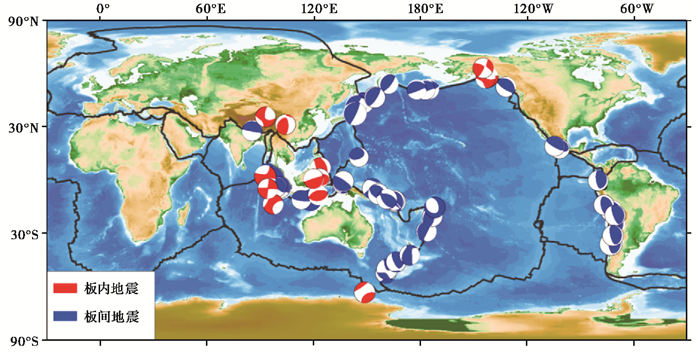
按照以上原则, 共挑选出全球58个独立的M_W≥7.8浅源地震序列, 其中, 8级地震序列26个, 9级地震序列2个。我国大陆及邻区共发生M_W≥7.8地震3次, 分别为2001年11月14日昆仑山口西7.8级、2008年5月12日汶川7.9级、2015年4月25日尼泊尔7.8级地震。这些地震主要分布在环太平洋地震带与欧亚地震带(图 2)。

2 地震序列类型的统计特征

考虑到序列类型早期判定的需要, 本文依据主震与3个月内最大余震之间的震级差ΔM进行序列类型划分, 划分标准如下(蒋海昆等, 2006)：

(1) 孤立型：ΔM≥2.5, 且余震次数较少；

(2) 主-余型：0.6≤ΔM≤2.4；

(3) 多震型：ΔM＜0.6, 多震型包含了双震型和震群型。

依据该划分标准对58次地震序列进行类型判定, 并按走滑型(S)、正断层型(N)和逆断层型(T)等3种典型震源机制解进行分类。这里按震源机制解中P轴、T轴倾角P_plug、T_plug进行简单分类, 当P_plug≤45°、T_plug≤45°时, 为走滑型机制；当P_plug＞45°时, 为正断层型机制；当T_plug＞45°时, 为逆断层型机制(苏有锦等, 2014)。

此外, 采用Kanamori等(1975)的分类方法, 把发生在板块边界附近, 但其发震断层面不是沿着板块边界的地震划分为板内地震。本文研究的是浅源地震, 所以将余震区长轴方向作为地震的发震断层分布方向。

2.1 地震序列类型与主震破裂方式

附表 1给出了58次巨大地震的基本参数, 包括发震时间、空间位置、震级、震源深度、震源机制解、余震区长度、最大余震、序列类型等。在58次地震中, 板内地震13次, 占总数的22.4%；其余77.6%为板间地震(图 2)。

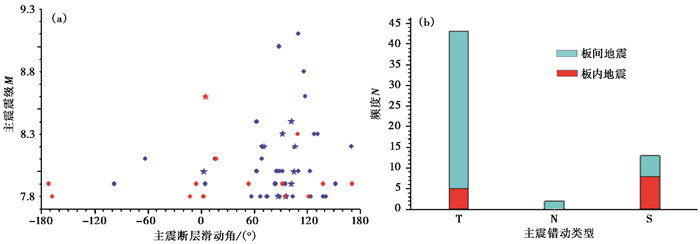
从主震断层的错动方式来看(图 3, 附表 1), 板间地震中74.1%为逆断层, 22.4%为走滑型。而对于板内地震, 61.5%为走滑型。即板间地震主要为逆断层型, 而板内地震主要为走滑型。全球61.5%的走滑型巨大地震发生在板内。

在58次巨大地震中, 主-余型48次, 占总数的82.8%, 其余17.2%为多震型。与5级以上地震不同, 巨大地震没有孤立型, 表明其余震比较活跃。在10次多震型地震中, 8次为逆断层型, 2次为走滑型(图 3(a))。在10次多震型地震中, 仅有1次为板内地震。板内地震中多震型仅占总数的7.7%, 而20%的板间地震为多震型。

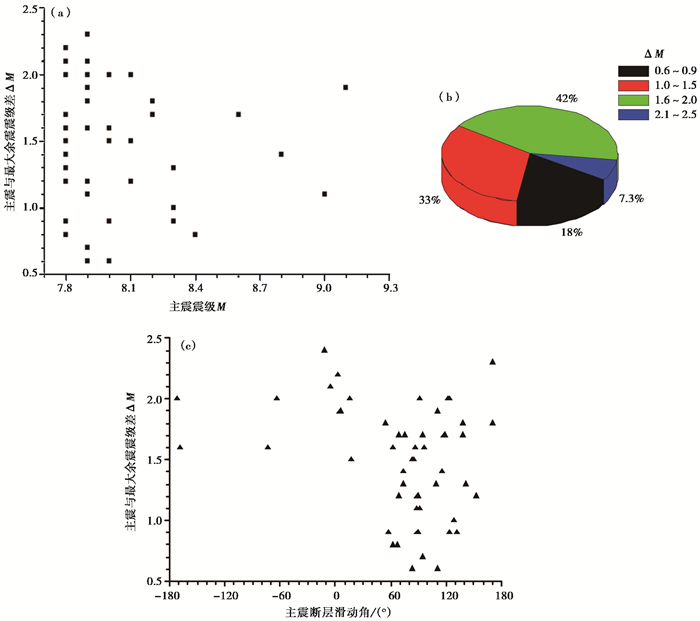
2.2 最大余震与主震的震级差、时间差和震中距离统计

统计所有主-余型地震的主震与最大余震震级差(简称震级差, 用ΔM表示), 结果显示(图 4(a)), 震级差与主震震级间没有统计关系, 对于7.8~7.9级地震, 震级差为0.6~2.4级, 而8级以上地震, 震级差为0.6~2.0级。对ΔM进行分段统计, 结果显示(图 4(b)), ΔM主要为1.6~2.0级、1.0~1.5级与0.6~0.9级, 分别占总数的42%、33%、18%, 即75%的主-余型地震ΔM为1.0~2.0级。

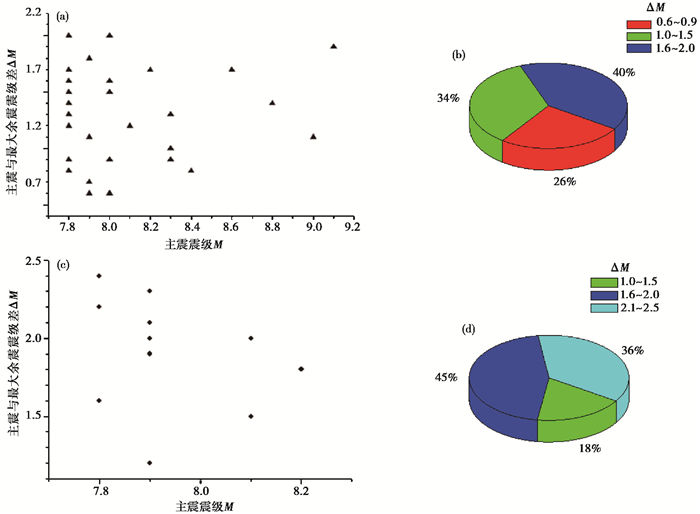
此外, 震级差ΔM与主震震源断层错动类型有关, 走滑型序列的震级差明显大于逆断层型(图 4(c))。在48次主-余型地震序列中, 主震为逆断层型的有35次, 走滑型11次, 正断层型2次。分别统计逆断层型和走滑型地震序列的震级差(图 5), 结果显示, 对于逆断层型序列, 震级差为0.6~2.0级(图 5 (a)), 其中, 40%的震级差为1.6~2.0级, 34%为1.0~1.5级, 26%为0.6~0.9级(图 5 (b))。而走滑型序列, 震级差为1.0~2.5级(图 5 (c)), 其中, 45%的震级差为1.6~2.0级, 36%为2.1~2.5级, 18%为1.0~1.5级(图 5 (d))。可见, 走滑型序列的震级差明显大于逆断层型。

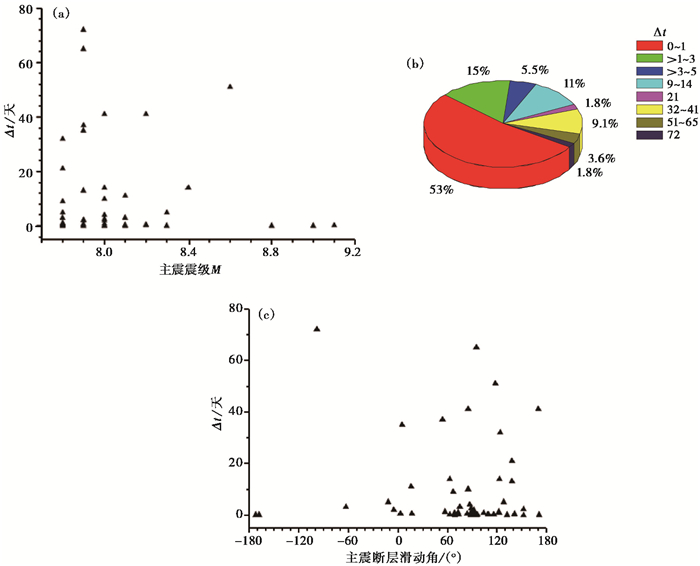
统计最大余震与主震发震时间差(简称时间差, 用Δt表示), 结果显示(图 6), 最大余震主要发生在主震后的半个月内, 占总数的83.6%。具体为, 53%的最大余震发生在主震后的24h内；15%的最大余震发生在主震后第1~3天；11%的最大余震发生在主震后第9~14天；9.1%的最大余震发生在主震后第32~41天。即68%的最大余震发生在主震后的3天内。此外, 约20%的最大余震发生在主震后10天左右与1个月左右。统计Δt与主震断层滑动角间的关系, 结果显示(图 6(c)), 最大余震发生的时间与主震断层错动方式间关系不明显。

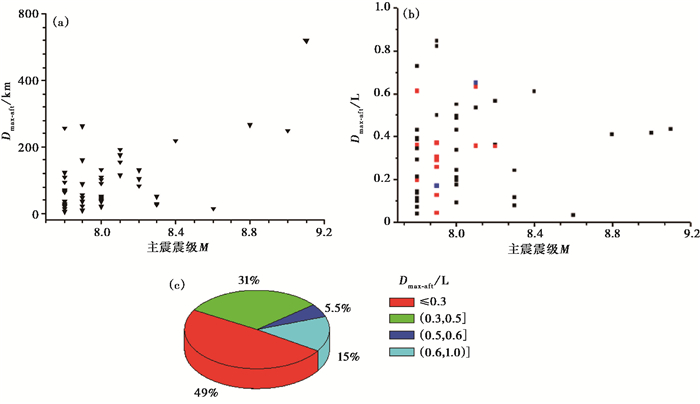
统计最大余震同主震震中距离(D_max-aft)与主震震级间的关系, 结果显示(图 7(a)), D_max-aft与主震震级间没有明显的统计关系。对于7.8~8.0级地震, 最大余震主要发生在距主震100km范围内, 占总数的75.6%；而对于8.1级以上地震, 最大余震主要发生在距主震100~300km范围内, 占总数的57.1%。

计算D_max-aft与余震区长轴比值, 并统计该比值的对数与主震震级间的关系(图 7(b))。结果显示, 该比值对数与主震震级间没有明显的统计关系。对于所有主-余型序列, 49%的D_max-aft不超过余震区长轴的1/3, 31%的D_max-aft为余震区长轴的1/3~1/2, 15%的D_max-aft大于余震区长轴的1/2(图 7(c))。

3 应用ETAS模型计算地震序列参数

本文使用ETAS模型计算全球巨大地震序列参数。ETAS模型假设所有余震均可以按照大森-宇津公式(Omori, 1895；Utsu, 1961)激发自己的余震, 且震级分布是独立的。假定主震的发生为初始零时刻, 在其后一个观测时段[0, T]内地震序列{(t_i, M_i)；i=1, 2, …, N}的强度函数可以表示为(Ogata, 1988)

$ \lambda \left(t \right)=\mu +K\sum\nolimits_{{{t}_{i}} < t}{\frac{{{\text{e}}^{\alpha \left({{M}_{i}}-{{M}_{0}} \right)}}}{{{\left(t-{{t}_{i}}+c \right)}^{p}}}, \ {{M}_{i}}>{{M}_{0}}} $

(1)

其中, t为主震发生后的离逝时间；M₀为计算所用序列的截止震级；M_i、t_i分别为第i个时间的震级及其距主震发震时刻的时间长度；μ为背景地震发生率；p表示序列衰减快慢；c为主震后余震频次达到峰值的时间长度；K表示余震的活跃程度；a表示触发次级余震的能力(Ogata, 1989、1992)。

使用最大似然法对ETAS模型进行参数估计(蒋长胜等, 2014)。为了保证有足够多的样本量, 本文挑选主震后1个月内发生的余震进行计算, 且计算每个序列的完备性震级, 当满足完备震级以上地震数量N≥50时, 计算序列参数。共计算了46个序列参数, 并对b值、a值和p值进行统计分析(表 1)。全部序列b值最小为0.685, 最大为1.651, 平均为1.164±0.211；p值最小为0.941, 最大为2.801, 平均为1.559±0.412。与前2个参数相比, a值分布最为分散, 范围为0~3.96, 平均为1.673±0.911。b值、p值和a值均呈现出Beta分布的特点(图 8(a)~8(c))。

主-余型序列b值平均为1.183±0.214, 多震型平均为1.079±0.188。板内序列b值平均为1.185±0.246, 板间平均为1.161±0.208。可见, 不同序列类型及板内、板间地震序列之间b值差异不显著。统计不同主震错动类型的平均b值可见, 逆冲型与走滑型非常接近, 均明显小于正断层型。但是正断层型序列仅有2个。从不同构造分区(图 8(d))计算结果来看, b值最小为南美板块西边界带(0.976), 最大为爪哇岛附近(1.299)。太平洋板块西边界带b值大于北美、南美板块的西边界带(表 1)。统计结果显示, 影响序列b值的主要因素为区域介质物性和应力状况等。

p值为序列的衰减率, p值越大, 则表示序列衰减越快。本文的计算结果显示(表 1), 不同序列类型及板内、板间地震序列平均p值差异不显著。走滑型、正断层型序列的平均p值非常接近, 分别为1.363±0.517、1.349±0.112, 而逆断层型序列平均为1.609±0.402。可见, 逆断层型序列p值明显大于走滑型和正断层型序列。这表明, 逆冲型序列衰减较快。从不同构造区平均结果来看, p值最小的区域为北美板块西边界带和太平洋板块北边界带, 约为1.2；太平洋板块西边界带为1.42~1.53；南美板块西边界带和苏门答腊附近为1.63~1.66；p值最大的区域爪哇岛及其附近区域, 约为1.81。显然, p值具有明显的分区特征(表 1)。

a值表示序列中不同震级地震产生高阶余震的能力。a值越小, 其“余震激发余震”的能力越强。本文的计算结果显示(表 1), 主-余型与多震型序列平均a值差异不大。板间、板内地震序列平均a值分别为1.550±0.862、2.185±1.211。显然, 板间序列平均a值明显小于板内序列。逆断层型序列平均a值最小(1.405±0.865), 其次是正断层型(1.904±0.039), 最大是走滑型序列(2.742±0.858)。这表明, 板间地震具有较强的触发次级余震的能力。逆断层型地震序列虽然衰减较快, 但其“余震激发余震”的能力却相对较强。不同构造区平均a值计算结果显示(表 1), a值最小的区域为爪哇岛附近, a值约为1.3；a值最大的区域为北美板块西边界带, a值约为3.33。

4 余震区规模与主震震级间关系的统计

震源破裂尺度与地震应力降或应变释放程度等物理过程有关(Wells et al, 1994；Biasi et al, 2006)。而余震区规模与震源破裂尺度大体相当, 所以研究余震区规模具有科学意义, 同时也有助于震后趋势判定(吴开统等, 1990)。许多学者对震源破裂尺度、平均滑动量等参数与震级进行统计, 通过线性拟和得到经验关系式(蒋海昆等, 2007a；Wells et al, 1994；李莹甄等, 2010)。其中, Wells等(1994)系统统计了由全球244个地震震源资料拟合得到的震源破裂尺度与震级间的关系。但是8级以上地震样本少, Wells等(1994)使用的总体统计样本的震级为M4.8~8.1, 逆断层型地震的统计样本仅为M5.4~7.4。不同研究者的统计数据不同, 得到的拟和关系也不同。近年来, 全球发生了多次8级以上大震, 特别是一些8.5级以上特大地震, 样本量的增多使得研究8级以上特大地震的震源破裂尺度与震级间的统计关系成为可能。

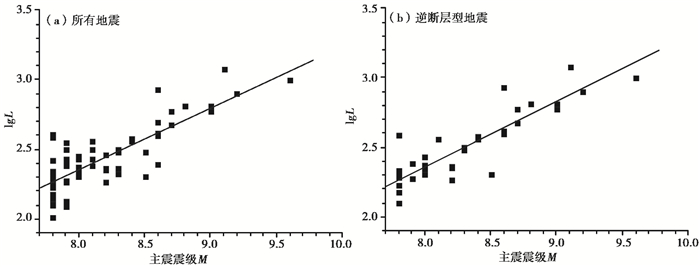
本文将全球1976年以来58次M_W≥7.8地震的余震区尺度作为震源破裂尺度(附表 1), 此外, 还补充了1900~1975年12次M_W≥8.5地震的震源破裂尺度(表 2)。拟和70次地震的震源破裂尺度对数与主震震级间的关系(图 9(a)), 得到的统计关系为

$ \lg L=\left(0.471\pm 0.039 \right){{M}_{\text{W}}}+\left(-1.408\pm 0.323 \right) $

(2)

其中, L为余震区长度, 单位km。由图 9(a)可见, 对于7.8~7.9级地震, 样本量较大, 但余震区规模比较分散。此外, 1957年3月9日阿拉斯加8.6级地震(震源破裂尺度达850km)和2004年12月26日印尼苏门答腊9.1级地震(余震区长达1200km)有些偏离拟和直线。应用全部样本得到的拟合公式(式(2))的标准差为0.133, 相关系数为0.830。统计逆断层型地震余震区尺度对数与主震震级间的关系(图 9(b)), 得到的拟合关系为

$ \lg L=\left(0.470\pm 0.037 \right){{M}_{\text{W}}}+\left(-1.399\pm 0.306 \right) $

(3)

拟合标准差为0.120, 相关系数为0.870。与所有样本都参与的统计相比, 逆断层型地震的拟合效果更好。

蒋海昆等(2007b)统计了我国大陆地区不同序列类型地震余震区尺度与主震震级、不同破裂类型地震余震区尺度与主震震级间的关系, 其中, 使用样本量最大(143)的为主-余型序列拟合的结果(式(3)), 相关系数为0.57, 拟合均方差为0.57。拟合线性关系最好的为走滑-近走滑型地震余震区尺度与主震震级, 公式如下所示, 其相关系数为0.68, 拟合均方差为0.325。与本文的结果相比, 蒋海昆等(2007a)统计结果的离散程度较高。

$ \lg L=\left(0.347\pm 0.042 \right){{M}_{\text{S}}}+\left(-0.622\pm 0.253 \right) $

(4)

Wells等(1994)给出的逆冲型地震的震源破裂尺度与矩震级间的关系为(统计范围为M_W5.4~7.4)

$ \lg L=\left(-2.86\pm 0.55 \right)+\left(0.63\pm 0.08 \right){{M}_{\text{W}}} $

(5)

陈培善等(1991)给出的破裂长度与面波震级间的关系式为(适用的震级范围为M_S7.8~8.5)

$ \lg L={{M}_{\text{S}}}-5.84 $

(6)

如果计算一个M_W8.0地震的破裂长度, 根据式(3)、(4)、(5)、(6)可分别得到破裂长度为229、143、151、115km。显然本文的结果比其他研究者的要大。这主要是因为蒋海昆等(2007b)使用M_S震级, 统计范围为5级以上, 且8级以上样本少。本文使用M_W震级, 统计范围为7.8~9.1级地震。Wells等(1994)的统计样本中没有涉及8级以上巨大地震, 而且其统计的震源破裂尺度主要来源于野外考察、地震波反演及各种结果的平均值(对于同一个地震, 如果有多个不同来源的震源参数, 又无法确定哪个最为准确, 则取平均值)。陈培善等(1991)给出的统计关系是基于二维破裂模式的地震定标律, 而地震定标律是建立在地震相似性基础上的, 地震相似性包括几何相似性、应力环境相似性和动力学相似性等。如果单个地震偏离相似性越远, 则相应估计值的误差就越大。对于同一个地震, 其余震区规模、野外考察得到的地表破裂带尺度及通过地震波反演得到的震源破裂规模有较大的差异。例如, 2001年11月14日我国昆仑山口西M_S8.1地震的余震区长约420km, 而野外考察地表破裂带的长度为425km(中国地震局监测预报司, 2002), 而震源破裂过程反演得到的滑动量大于0.5m的区域长600km(许力生等, 2004)。野外考察的结果受破裂出露地表情况的影响；波形资料反演结果主要受震源模型、资料的空间分辨率等因素的影响；余震区尺度受地震定位精度的影响较大。当地震定位精度较高时, 余震区规模可以较好地反映震源破裂的尺度。

5 结论与讨论

本文系统研究了1976年以来全球58次M_W≥7.8浅源地震序列的统计特征, 包括序列类型划分、最大余震与主震的震级差、时间差和震中距离等。取主震后1个月内的余震数据, 应用ETAS模型计算了46次地震序列参数, 并从板内、板间地震及主震破裂类型等角度讨论计算结果。主要得到以下几点结论：

(1) 1976年以来全球共发生58次7.8级以上浅源地震, 其中, 板内地震13次, 板间地震45次, 板内地震与板间地震数量之比为1/3.46。与板间地震相比, 板内地震强度低。

(2) 在板间地震中, 74.1%为逆断层, 而61.5%的板内地震为走滑型。即板间地震主要为逆断层型, 而板内地震主要为走滑型。

(3) 在58次巨大地震中, 82.8%为主-余型, 其余17.2%为多震型。与5级以上地震不同, 巨大地震没有孤立型, 表明其余震较活跃。在板内地震中, 多震型仅占总数的7.7%；板间地震中, 多震型地震占总数的20%。

(4) 对主-余型地震, 75%的主震与最大余震的震级差为1.0~2.0级。震级差与主震震源断层错动类型有关。逆断层序列的震级差为0.6~2.0级, 其中, 74%的震级差为1.0~2.0级；而走滑型序列的震级差为1.0~2.5级, 其中, 81%的震级差为1.6~2.5级。即走滑型序列的震级差明显大于逆断层型序列。

(5) 在主-余型序列中, 53%的最大余震发生在主震后24h内, 15%发生在主震后第2~3天, 11%发生在主震后第9~14天。最大余震发生时间与主震断层错动方式间的关系不明显。49%的D_max-aft(主震震中与最大余震震中之间的距离)不超过余震区长轴的1/3, 31%的D_max-aft为余震区长轴的1/3~1/2, 15%的D_max-aft大于余震区长轴的1/2。D_max-aft与主震震级及主震错动类型间没有明显的统计关系。

(6) 应用ETAS模型计算了46次序列参数。b值平均为1.164±0.211, p值平均为1.559±0.412, a值平均为1.673±0.911。与前2个参数相比, a值分布最为分散。b、p、a值均呈Beta分布。不同序列类型、不同震源机制及板内、板间地震序列b值差异不显著, 不同构造区域b值差异较明显。不同序列类型及板内、板间地震序列平均p值差异不明显, 而主震错动类型对p值有影响, 逆断层型序列p值明显大于走滑型和正断层型。与b值相似, p值也具有明显的构造分区特征。不同序列类型的平均a值差异不明显。板间序列平均a值明显小于板内序列, 逆断层型序列明显小于走滑和正断层型。这表明, 板间地震具有相对较强的触发次级余震的能力, 逆断层型地震序列虽然衰减较快, 但“余震激发余震”的能力相对较强, 这与震级差(主震与最大余震的震级差)的统计结果一致。a值也具有明显的构造分区特征。

(7) 本文统计了巨大地震, 特别是逆断层型大震余震区规模与主震震级间的关系。结果表明, 余震区长轴对数与主震震级间呈正相关关系, 其中, 逆断层型地震的拟合结果优于所有样本的统计结果。

以上统计结果对大震后的趋势判定具有实践意义和减灾意义。此外, 本文比较了不同序列类型、不同震源错动类型及板内、板间地震序列参数的共性和差异性, 其结果对于科学研究具有一定的参考价值。由于构造分区样本量较少, 所以对于序列参数区域性差异性没有进行深入分析。