地震序列是地震活动的主要表现形式之一,是统计地震学的重要研究对象。不同的构造区域、地震序列类型、震源区构造应力水平和区域大地热流值等均可能表现为地震序列参数的差异(Kagan et al,2010),且余震序列的衰减特征和激发余震的能力可通过序列的统计参数来表征,因此,获得准确可靠的地震序列参数对快速判定地震序列类型、研究震源区特征和评估后续地震危险性等均具有重要的参考价值(蒋海昆等,2007;Guo et al,1997)。目前国际上对地震序列参数的计算主要采用时间序列的“传染型余震序列”(epidemic type aftershock sequence,简称ETAS)模型(Ogata,1988、1989;Zhuang,2011)。蒋海昆等(2006)系统研究了中国大陆5级以上地震序列的统计特征,并从物理上讨论了不同条件下的序列衰减和余震激发问题。蒋长胜等(2013a、2013b、2013c)对1976年唐山地震序列、2013年岷县漳县MS6.6地震序列和芦山MS7.0地震序列利用ETAS模型进行了研究。余娜等(2016a、2016b)采用时间序列的ETAS模型计算了2010年玉树MS7.1、2016年门源MS6.4地震序列。
青海地区是西北地震活动最为活跃的地区之一,是地震学家高度关注的地震危险区域,历史上多次强震的发生,积累该区域内更多、更可靠的地震序列参数,有利于震后地震趋势估计和余震危险性研究。
1 研究资料 1.1 时间序列ETAS模型用于拟合地震序列的ETAS模型(Ogata,1988、1989;Zhuang,2011),其假设所有的余震均可按照大森-宇津公式(Omori,1894;Utsu,1961)激发自己的余震
| $f\left(t \right) = \mathit{\mu + K/}{\left({t + c} \right)^p} $ | (1) |
式中,f(t)为t时刻对应的地震序列发生率; t为主震发生后的离逝时间; μ为背景地震发生率; p表示余震序列衰减的快慢; c为主震后余震频次达到峰值时所对应的时间; K为常数,用于描述余震的活跃程度。ETAS模型假定主震的发生为初始零时刻,在其后的一个观测时间段[0,T]内的地震序列{(ti,Mi);i=1,2,…,N}的强度函数可表示为(Ogata Y,1988)
| $\mathit{\lambda }\left(t \right) = \mathit{\mu + K}\sum\limits_{{t_\mathit{i}} < t} {\frac{{{\rm{e}}\mathit{\alpha }\left({{M_i} - {M_0}} \right)}}{{{{\left({t - {t_i} + c} \right)}^p}}}}, {M_i} > {M_0} $ | (2) |
其中,Mi和ti分别为第i个事件的震级和发生时间;M0为参考震级,一般可取截止震级。式(2)中的参数p表示地震序列衰减的快慢,p越大衰减越快,反之则越慢;参数α表示触发次级余震的能力(Ogata,1989),α越大表示触发次级余震的能力越弱,反之亦然。对于震群型序列,一般情况下α<1,而当地震序列中无明显的被激发的次级余震时,α一般大于1(Ogata,2001);参数c为数值极小的正常数,一般用于调节当地震序列在主震发生后极短时间内余震记录不完整,以及避免式(2)中分母为0的情况。为确保参数拟合的稳定性,当区域内背景地震发生率不高时,可通过设置背景地震的发生率μ=0来降低拟合难度。
1.2 研究区域和序列目录完整性分析本文选取的“青海地区”的空间范围为32.0°~39.0°N,89.5°~103.0°E。该研究区域位于青藏高原中北部及东北缘,地质构造规模大、活动性强,主要有阿尔金断裂带、祁连山-河西走廊活动断裂带、昆仑山断裂带、巴颜喀拉断裂带和唐古拉断裂带等,以NNW、NW-NWW向断裂带最为发育。地震具有频次高、强度大、分布广的特点(马玉虎等,2006;曾秋生,1999)。2009年以来研究区主震震级MS≥5.0地震有12个,其中,5.0≤MS<6.0的有8个,6.0≤MS<7.0的有3个,MS≥7.0的有1个。受ETAS模型计算对地震序列质量的要求,本文使用了记录较好的5级以上地震序列共9个(图 1),分别为2009年8月28日大柴旦MS6.4、2010年3月24日西藏聂荣MS5.8、2010年4月14日玉树MS7.1、2011年6月26日囊谦MS5.2、2013年1月30日杂多MS5.2、2013年9月20日门源MS5.1、2015年11月23日祁连MS5.0、2016年1月21日门源MS6.4和2016年10月17日杂多MS6.2地震。
|
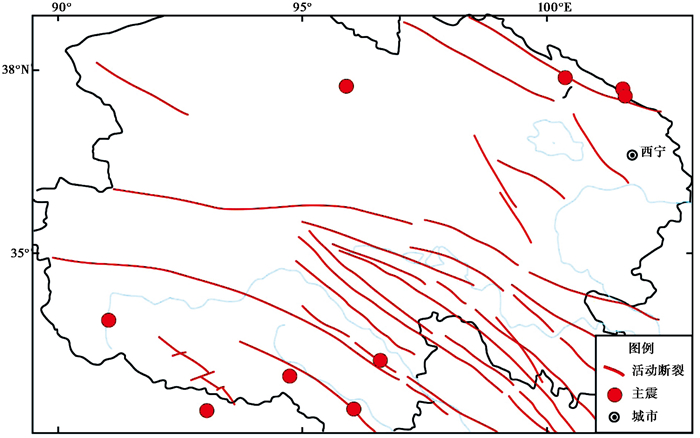
图 1 研究区9个地震序列主震的空间分布 |
本研究所采用的地震目录为中国地震台网中心提供的《全国统一正式目录》。青海地区地震目录存在着明显的空间不均匀现象,说明不同时期、不同地区地震记录水平存在明显的差异。在实际的地震序列选取中,采用了蒋长胜等(2014)区分地震序列与背景地震的时-空分布界限的“自然边界法”,通过纬度-时间图、经度-时间图及震中分布图相结合的方式选取地震序列。图 2给出了2009年大柴旦MS6.4地震序列的选取结果。依照上面的选取方法,选取了其余8个地震序列。此外,由于在一些强震发生后的短期内,主震的波形振幅较大,面波等波列持续时间较长,可出现将随后大量发生的震级较小的余震“淹没”而导致余震区甚至更大范围内的地震监测能力显著降低(Akaike,1974)的现象。为确保地震序列的完整性,采用“震级-序号”法(Huang,2006;蒋长胜等,2014;Zhuang et al,2012)确定了每个地震序列完整性震级Mc(图 3)。“震级-序号”法按地震发生时间的先后顺序排序,地震密度较大的区域的连线大致为截止震级Mc的时序变化。
|
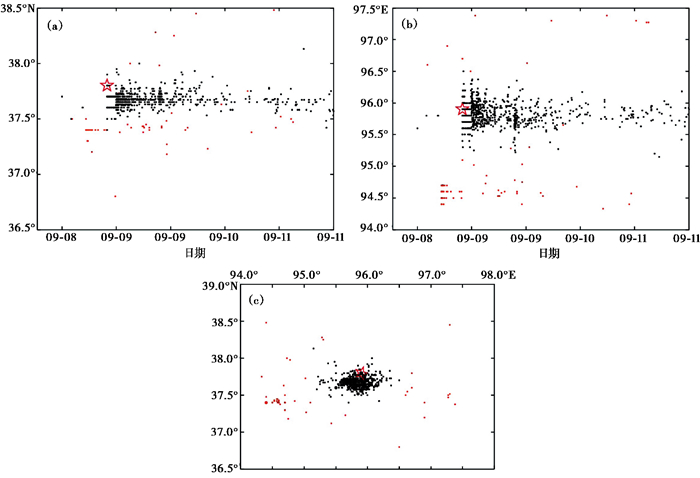
图 2 2009年大柴旦MS6.4地震序列的选取结果
(a)纬度-时序分布结果;(b)经度-时序分布结果;(c)空间分布结果 红色五角星代表主震;黑色圆点代表用自然边界法获得的地震序列;红色圆点为背景地震 |
|
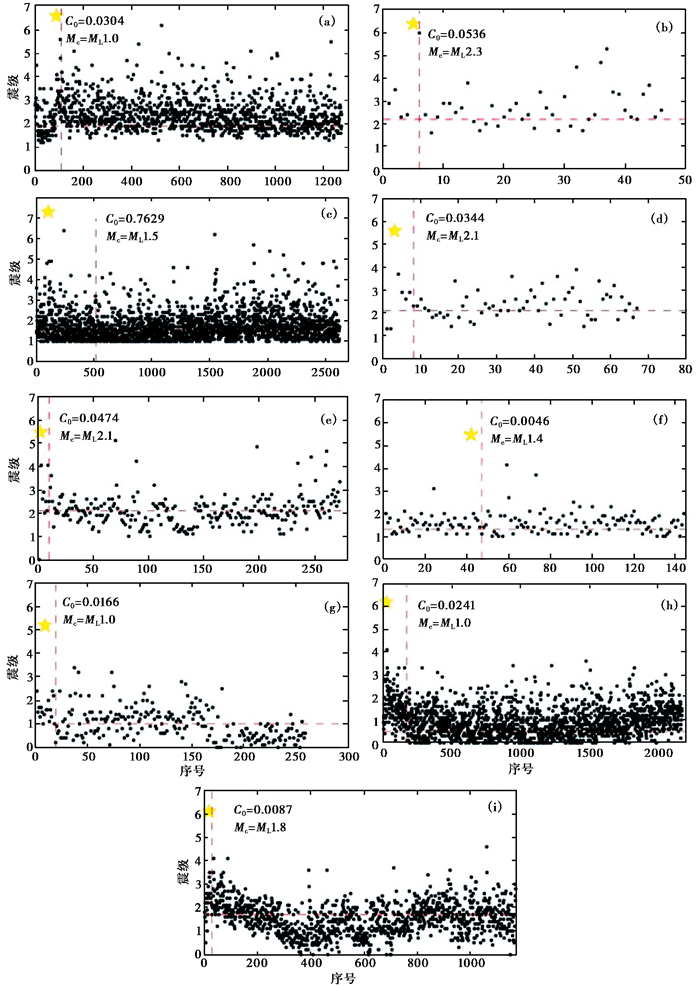
图 3 研究区9个地震序列的“震级-序号”法处理结果
黄色五角星为主震,黑色圆点为地震事件 (a)2009年8月28日大柴旦MS6.4地震;(b)2010年3月24日西藏聂荣MS5.8地震;(c)2010年4月14日玉树MS7.1地震;(d)2011年6月26日囊谦MS5.2地震;(e)2013年1月30日杂多MS5.2地震;(f)2013年9月20日门源MS5.1地震;(g)2015年11月23日祁连MS5.2地震;(h)2016年1月21日门源MS6.4地震;(i)2016年10月17日杂多MS6.2地震 |
ETAS模型参数一般使用最大似然法进行估计。在拟合时间[S,T]范围内(0<S<T),似然函数L的形式为
| $\lg \mathit{L = }\sum\limits_{i:S \le {t_\mathit{i}} < T} {\lg \mathit{\lambda }\left({{t_\mathit{i}}} \right)} - \int_S^T {\mathit{\lambda }\left(t \right){\rm{d}}\mathit{t}} $ | (3) |
将式(2)带入式(3),即可对序列参数[μ,K,c,α,p]进行最大似然估计。作为示例,图 4给出了2009年海西MS6.4地震序列在Mc=ML1.9情况下的ETAS模型参数结果,获得ETAS模型参数为μ=0.0000,K=0.0280,c=0.0035,α=1.2411和p=1.2650。为进一步考察ETAS模型的拟合效果,常使用“转换时间”域的“残差分析”法(Ogata,1988)。“残差分析”方法可将复杂的地震序列{ti}转换为齐次泊松过程,并在“转换时间”域{τ}中进行拟合效果分析,相应的转换过程为
|
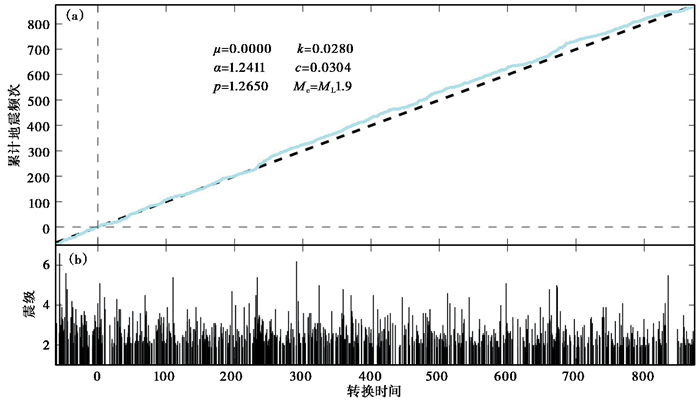
图 4 2009年8月28日大柴旦MS6.4地震序列拟合情况的“残差分析” (a)累计地震数(蓝色实线)与ETAS拟合曲线(虚线)在稳态泊松分布的“转换时间”域的比较;(b)M-τ图,“转换时间”域的地震序列 |
| $t \mapsto \mathit{\tau = \Lambda }\left(t \right) = \int_0^t {\mathit{\lambda }\left(u \right){\rm{d}}\mathit{u}} $ | (4) |
这种经过转化的{τ}域的数据被称为“残差点过程”(RPP)。若在残差分析中,转换时间域的RPP在{τ}上的累计频次近似直线,并与理论直线较为接近(Zhuang et al,2012),则ETAS模型拟合效果较好。以2009年大柴旦MS6.4地震序列为例,图 4(a)给出了主震之后0~91天和Mc=ML1.9时的“残差分析”结果,可以看出,序列累计地震数与理论ETAS拟合曲线较为接近,ETAS模型对此地震序列的拟合较为理想;图 4(b)为相应的{τ}域的M-τ分布。研究区9个地震序列参数的估算结果见表 1。
| 表 1 研究区9个地震序列主震参数和地震序列ETAS模型参数值 |
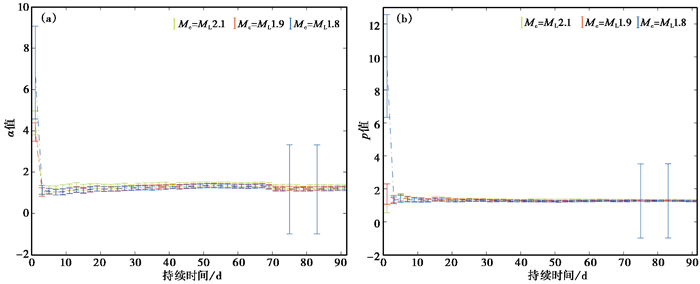
ETAS模型参数与截止震级的选取有一定的关系(蒋长胜等,2013a、2013b)。本文以2009年8月28日大柴旦MS6.4、2010年4月14日玉树MS7.1地震为例,研究了不同截止震级对地震序列参数的影响。2009年大柴旦MS6.4地震选取截止震级Mc=ML1.8、1.9、2.1,发现地震序列参数α值和p值在Mc=ML2.1时变化较小,误差也小(图 5)。2010年玉树MS7.1地震选取截止震级Mc=ML1.5、1.6、…、2.1,当截止震级Mc从ML1.5到2.1逐渐增大时,α值和p值随截止震级的变化均有较大变化,参数k值逐渐减小,α值总体上有增加的趋势,p值随截止震级的增大而减小,但是变化幅度不大。因此,在考察地震序列参数的早期特征时,须考虑在何种截止震级条件下进行讨论。
|
图 5 2009年8月28日大柴旦MS6.4地震ETAS模型计算结果 (a)不同截止震级下α值随拟合截止时间的变化;(b)不同截止震级下p值随拟合截止时间的变化 |
由于板内地震所处的构造运动速率不同,故地震序列持续时间存在明显差异。因此,所选取的地震序列的拟合截止时间不同,获得的ETAS模型参数可能不同,拟合参数的标准差也将存在差异(Iwata,2008)。以2010年4月14日青海玉树7.1级地震为例,设定tend=[1.0,2.0,3.0,…,42.0],当Mc=ML1.5时,ETAS模型参数α值和p值均在震后14天出现突跳变化,标准差幅值较大,尤其是激发次级余震能力的α值变化最为剧烈,p值在震后18天内有一定幅度波动。b值变化相对稳定,但在震后14天内有逐渐增加的变化,随着序列持续时间的增加α值减小。地震早期ETAS模型参数的α值、p值变化幅度较大,其后,趋于相对稳定。
3 青海地区地震序列参数的时变特征地震序列参数的早期变化比较剧烈,反映了地震序列主震发生后应力快速调整的过程,余震也主要集中发生在地震早期阶段。为了研究地震序列参数在时间上的变化特征,本文将地震序列不同截止条件下的ETAS模型参数稳定时间和震级进行统计(表 2),可以看出,地震序列以不同的截止震级作为研究对象时,地震序列的稳定时间Tα和Tp是不同的,也就是说,在一个地震序列中,地震序列参数α值和p值的稳定时间Tα和Tp与截止震级没有明显的正相关关系,当Mc=ML1.8时,Tα=19,Tp=19;当Mc=ML1.9时,Tα=17,Tp=21;当Mc=ML2.1时,Tα=23,Tp=19。地震序列参数α值和p值的稳定时间Tα和Tp与主震震级间没有明显的相依关系,主震震级较大的其稳定时间也可能较短,震级较小的地震稳定时间反而较长。比如玉树MS7.1地震,地震序列参数α值和p值的稳定时间为:当Mc=ML2.0时,Tα=15,Tp=15;杂多MS5.2地震,当Mc=ML2.0时,Tα=18,Tp=13;反映了玉树7.1地震震后应力迅速调整的特征。
| 表 2 地震序列参数稳定时间统计表 |
研究区不同震级档地震序列参数的最长稳定时间和最短稳定时间分别为:地震序列主震震级MS5.0~6.0,Tα,min=9,Tα,max=47,Tp,min=13,Tp,max=45;主震震级MS6.0~7.0,Tα,min=17,Tα,max=57,Tp,min=11,Tp,max=26。
4 讨论与结论为系统考察青海地区地震序列的ETAS模型,并对地震序列的震后早期特征进行分析,本文运用中国地震台网中心提供的《全国统一正式目录》,对青海地区的地震序列进行了筛选,发现青海地区地震目录存在着明显的空间不均匀现象,不同时期、不同地区地震记录水平存在明显的差异。在实际的地震序列选取中采用“自然边界法”选取了研究区2009年以来的9个地震序列,利用“震级-序号”法确定了每个地震序列的完整性震级Mc,使用最大似然法对每个地震序列进行参数估算,获得了如下认识:
(1) 为检测地震序列参数的稳定性,考察了截止震级和拟合截止时间的选取对ETAS模型参数影响。研究发现,截止震级Mc对α、k和p值有一定的影响。在考察地震序列参数的早期特征时,须考虑在何种截止震级下进行讨论;地震早期ETAS模型参数的α值、p值变化幅度较大,反映了地震主震发生后震源区应力的快速调整过程,其后,地震参数的α值和p值趋于相对稳定。
(2) 青海地区地震序列的ETAS模型参数α值、p值的稳定时间Tα、Tp与截止震级间没有明显的正相关关系,与主震震级间也无明显的相依关系,主震震级较大的地震事件稳定时间可能较短,震级较小的地震事件其稳定时间也有可能较长。
(3) 青海地区不同震级档地震序列参数的最长稳定时间和最短稳定时间分别为:地震序列主震震级MS5.0~6.0,Tα,min=9,Tα,max=47,Tp,min=13,Tp,max=45;主震震级MS6.0~7.0,Tα,min=17,Tα,max=57,Tp,min=11,Tp,max=26。
由于研究区域强震数目和ETAS模型计算条件所限,仅对9个地震序列进行了估算,并对其时间特征进行了讨论,且所得出的结论仅反映部分统计特征,今后还需要继续积累更多的震例进行更深入研究。
致谢: 研究中使用了中国地震台网中心“全国地震编目系统”提供的“统一正式目录”,日本统计数理研究所庄建仓教授编制、提供了本文所使用的ETAS模型和余震短期概率预测程序,在此一并表示感谢。
马玉虎、陈玉华, 2006, 青海及邻区强震迁移活动规律分析, 地震地磁观测与研究, 27(1): 18-25. DOI:10.3969/j.issn.1003-3246.2006.01.004 |
蒋长胜、韩立波、郭路杰, 2014, 新疆于田地区2008年以来3次地震序列参数的早期特征, 地震学报, 36(2): 165-174. DOI:10.3969/j.issn.0253-3782.2014.02.002 |
蒋长胜、吴忠良、韩立波等, 2013a, 地震序列早期参数估计和余震概率预测中截止震级Mc的影响:以2013年岷县漳县6.6级地震为例, 地球物理学报, 56(12): 4048-4057. |
蒋长胜、吴忠良、庄建仓, 2013b, 地震的"序列归属"问题与ETAS模型——以唐山序列为例, 地球物理学报, 56(9): 2972-2981. |
蒋长胜、庄建仓、龙锋等, 2013c, 2013年芦山MS7.0地震序列参数的早期特征:传染型余震序列模型计算结果, 地震学报, 35(5): 661-669. |
蒋海昆、曲延军、李永莉等, 2006, 中国大陆中强地震余震序列的部分统计特征, 地球物理学报, 49(4): 1110-1117. DOI:10.3321/j.issn:0001-5733.2006.04.024 |
蒋海昆、郑建常、吴琼等, 2007, 传染型余震序列模型震后早期参数特征及其地震学意义, 地球物理学报, 50(6): 1778-1786. DOI:10.3321/j.issn:0001-5733.2007.06.018 |
余娜、蒋长胜、马玉虎, 2016a, 2010年青海玉树MS7.1地震序列ETAS模型参数及其变化特征研究, 地震工程学报, 38(4): 609-615. |
余娜、张晓清、袁伏全, 2016b, 2016年青海门源6.4级地震余震序列参数稳定性分析, 地震研究, 39(增刊Ⅰ): 61-67. |
曾秋生, 1999, 青海地震综合研究, 49~51, 北京: 地震出版社.
|
Akaike H, 1974, A new look at the statistical model identification, IEEE Trans Automat Control, AC-19: 716-723. |
Guo Z, Ogata Y, 1997, Statistical relations between the parameters of aftershocks in time space, and magnitude, J Geophys Res, 102(B2): 2857-2873. DOI:10.1029/96JB02946 |
Iwata T, 2008, Low detection capability of global earthquakes after the occurrence of large Earthquakes:Investigation of the Harvard CMT catalogue, Geophys J Int, 174(3): 849-856. DOI:10.1111/gji.2008.174.issue-3 |
Huang Q, 2006, Search for reliable precursors:A case study of the seismic quiescence of the 2000 western Tottoriprefecture earthquake, J Geophys Res, 111(B4): B04301. |
Kagan Y Y, Bird P, Jackson D D, 2010, Earthquake patterns in diverse tectonic zones of the globe, Pure Appl Geophys, 167(6/7): 721-741. |
Ogata Y, 1988, Statistical models for earthquake occurrences and residual analysis for pointprocesses, J Amer Statist Assoc, 83(401): 9-27. DOI:10.1080/01621459.1988.10478560 |
Ogata Y, 1989, Statistical model for standard seismicity and detection of anomalies by residualanalysis, Tectonophysics, 169(1/2/3): 159-174. |
Ogata Y, 2001, Increased probability of large earthquakes near aftershock regions with relativequiescence, J Geophys Res, 106(B5): 8729-8744. DOI:10.1029/2000JB900400 |
Omori F, 1894, On aftershocks of earthquakes, J Coll Sci Imp Univ Tokyo, 7: 11-200. |
Utsu T, 1961, A statistical study of on the occurrence of aftershocks, Geophys Mag, 30: 521-605. |
Zhuang J C, 2011, Next-day earthquake forecasts for the Japan region generated by the ETASmodel, Earth Planets Space, 63(3): 207-216. |
Zhuang J, Harte D, Werner M J, et al, 2012, Basic models of seismicity: temporal models, Community Online Resource for Statistical Seismicity Analysis, doi: 10.5078/corssa-79905851.
|
 2018, Vol. 34
2018, Vol. 34


