山西2015地壳速度模型研究
殷伟伟, 陈存田, 宋秀青, 李自红, 梁向军, 朱元清
中国地震  2018, Vol. 34 2018, Vol. 34 Issue (4): 720-730 Issue (4): 720-730
|
山西地区(34°~41°N,110°~115°E)位于华北克拉通内部,东部为华北平原地块,西部为鄂尔多斯地块,二者在结构和稳定性方面存在较大差异(张培震等,2003)。华北平原地块在燕山期由典型稳定的克拉通地块转变为造山带(邓晋福等,2003),鄂尔多斯地块自形成以来保持了典型的大陆克拉通岩石圈结构特征(邱瑞照等,2004)。山西地区处于2个构造特征截然不同的地质体之间,地壳运动十分活跃,导致山西断陷带成为我国一条重要的地震活动带,地震活动非常频繁。因此,需要利用精准的地震定位结果来正确把握该地区发震构造、地震活动性和地震触发过程等(宋美琴等,2012)。当前,山西测震台网的测震台站已基本确定,地震定位精度主要受地壳速度模型的制约。若要获得精准的地震定位结果必须具备当地可靠的地壳速度模型,所以开展山西地区地壳速度模型研究有着重要的意义。
目前,受定位程序以及计算成本等因素的影响,测震台网日常工作中所使用的速度模型以一维速度模型为主(孙安辉等,2011)。2015年以前,山西测震台网使用的定位模型是在J-B模型(Jeffreys et al,1940)的基础上进行修正后得到的,简称“修正的J-B模型”。该走时模型的编制是以欧亚大陆平均速度为基础,适用于大区域范围内的地震观测资料。山西地区地质构造复杂,莫霍面深度以及速度结构在SN、EW方向都有较大差异(张曼丽,1994)。对此有诸多学者曾经对山西不同地区速度模型做过研究,成果与与修正的J-B模型存在较大差异(张学民等,2004;于利民等,1995;祝治平等,1999;徐扬等,1997;魏文博等,2007;张健狮等,1997;张学民等2003;郭震等,2015),鲜有针对适用于山西全区地壳速度模型的研究。
针对上述问题,本文依据山西测震台网2009~2014年大量实测地震数据,对山西地区速度模型进行了分析研究,为提高地震定位精度、减小残差提供了模型基础。首先通过线性拟合获得模型的速度参数的波动范围,在此基础上,利用“折合走时”法确定了康氏界面和莫霍界面深度的范围;然后通过Hyposat程序确定了“山西2015地壳速度模型”(2015年完成的山西一维地壳速度模型)的各个参数;最后采用批量定位比较残差、PTD测定深度和人工爆破等3种方法对新模型进行了验证。
1 数据选取及其预处理本研究旨在求得一组符合山西地区的速度模型参数,震相数据选自山西测震台网2009~2014年记录的山西及周边50km范围内的地震事件,并且地震事件记录的台站数N≥10个的地震数据作为原始数据。按照不同的震级档,对Pn、Pg、Sn和Sg震相数进行统计,见表 1。
| 表 1 不同震级的震相个数 |
为保证所选地震的震中具有较高的精度,将震相数据进行预处理,只保留参与定位的台站数大于40的一类精度地震事件,同时剔除Pn震相个数小于4个的地震事件。依照上述条件共得到76个地震事件,获取Pg震相3118个、Pn震相1090个,将此作为研究山西地区一维地壳速度模型的基础数据,震中分布射线图如图 1。由图 1可知,预处理后的76个地震的震中较均匀地分布在山西地区,而且震中与台站的连线几乎覆盖了整个山西地区,具有较强的代表性。

|
图 1 预处理得到的76个地震分布及地震射线 |
速度模型中的速度包括3种震相的波速,即Pg的速度值v1、Pb的速度值v2和Pn的速度值vn。其中v1和vn波动范围采用在不同震中距范围内实测数据线性拟合与滑动窗拟合相结合的方法确定;由于Pb震相的标注存在一定困难,日常速报和编目中均未对其做出要求,因此数据量较少,只用线性拟合来确定v2。
2.1 v1和vn波动范围的确定根据预处理得到的76个地震事件,提取Pn和Pg震相的走时及震中距,分别将每种震相的走时和震中距进行线性拟合。这里的线性拟合实质是求走时Y和震中距X之间的线性函数关系
| ${Y_\mathit{i}} = \mathit{A + B}{\mathit{X}_\mathit{i}}{\rm{\;\;\;\;}}\left({i = 1, 2, \cdots, n} \right) $ | (1) |
其中,(Xi,Yi)表示(X,Y)的第i个实测值;A和B为任意实数。
针对不同震中距范围内的走时分别采用上述方法进行拟合计算,结果见表 2。可以看出,vn随着震中距的增大逐渐增大,由7.70km/s增大到8.06km/s,当Δ=50~450km时达到最大值;v1与vn的情况相近,当Δ=50~150km时为最小值6.01km/s,随着震中距的增大呈逐渐增大的趋势,并且震中距达到Δ=50~450km后趋于稳定。震中距较小时vn值偏小主要是由于这段震中距范围内Pn震相个数有限造成。
| 表 2 震中距在不同范围内拟合结果 |
滑动窗拟合的方法能够更进一步分析该地区地壳速度结构分段速度的稳定性(陈向军等,2014)。本节基于预处理得到的76个地震,分别给出Pn和Pg两种震相的震中距在不同区域范围内的速度变化(表 3、4),由表 3、4可知:
| 表 3 震中距在不同区域范围内的速度变化状况(步长=150km) |
| 表 4 震中距在不同区域范围内的速度变化状况(步长=200km) |
(1) 震中距以150km为步长滑动时,vn值呈窄幅波动的趋势,最大值为8.08km/s,最小值为7.77km/s;v1值的波动范围也较小,围绕6.20km/s波动,最大值为6.23km/s,最小值为6.12km/s。
(2) 震中距以200km为步长滑动时,vn和v1值的波动范围进一步缩小且趋于稳定。vn最大值为8.05km/s,最小值为7.81km/s;v1最大值为6.21km/s,最小值为6.15km/s。
由上述2种计算方法可得:山西地区v1=6.00~6.30km/s,平均值为6.15km/s;vn=7.80~8.10km/s,平均值为7.95km/s。
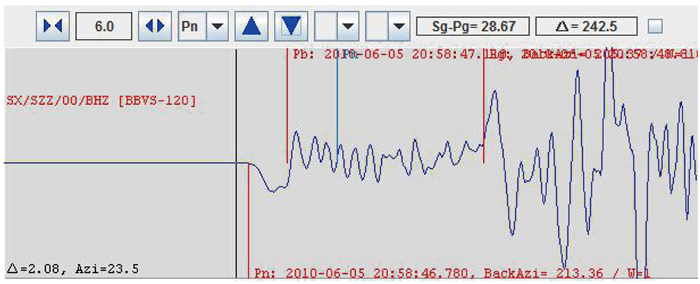
2.2 v2范围的确定为了能够更精确研究山西地区的地壳速度模型,在预处理的同时对得到的76个地震进行识别并标定Pb震相,共得到136个Pb震相,山西地区比较典型、清晰的Pb震相如图 2所示。
|
图 2 山西地区典型Pb震相 |
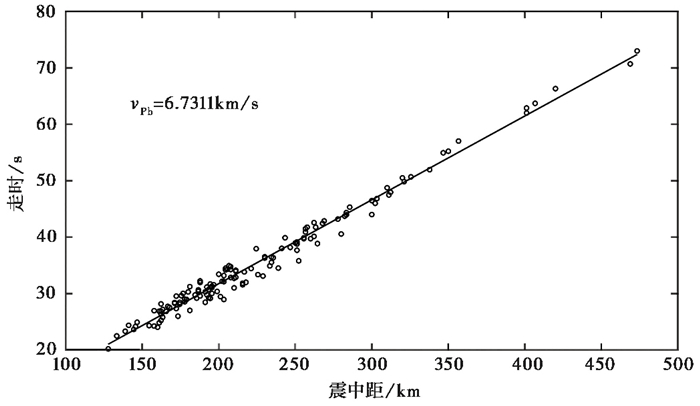
将上述136个Pb震相的走时与震中距进行线性拟合,得到Pb的速度值v2=6.73km/s(图 3)。
|
图 3 Pb震相线性拟合 |
参考目前全国各个台网使用的速度模型,其中J-B模型、IASPA91模型、甘青模型和陕西模型中v2=6.50km/s,华南模型中v2=6.88km/s。所以可以认为山西地区v2=6.50~6.90km/s,平均值为6.70km/s。
3 速度模型中界面埋深范围的确定本文采用理论和实测走时相对比的方法确定康氏面和莫霍界面深度的波动范围。由于理论走时依托速度模型,合理的模型计算的理论走时和精度较高的实测走时具有较好的拟合程度,因此通过调整模型参数改变二者拟合程度可以确定模型参数的波动范围。为了能够清晰、直观地表示震中距与走时间的关系,先对走时进行处理,得到“折合走时”tZ,然后给出“折合走时”和震中距关系。
| ${t_{\rm{Z}}} = t - \left({\mathit{\Delta /v}} \right) $ | (2) |
式中,tZ为折合走时;t为走时;Δ为震中距;v为波速。
此方法的基本思路是:根据模型参数和本地区震源深度分别求得Pb和Pn震相在一定震中距范围内不同震源深度处的理论走时,由各个台站的震相到时和震中距可以获取相应震中距范围内的实测走时;对理论走时和实测走时分别进行处理得到理论“折合走时”和实测“折合走时”,保持模型中速度值不变,通过调整深度值改变二者拟合程度,进而确定康氏面和莫霍界面深度的波动范围。
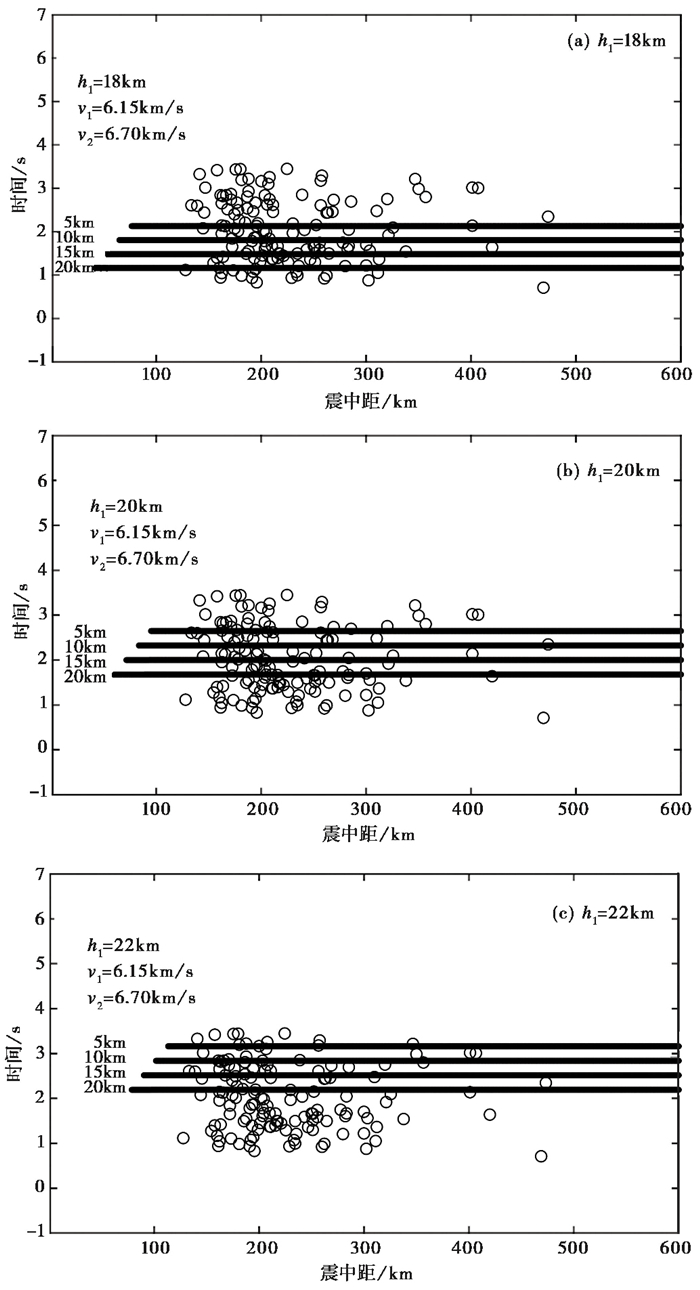
由于本节的目标是初步确定模型参数的波动范围,因此速度值v1、v2和vn分别取前文求得波动范围的平均值6.15、6.70和7.95km/s,实测走时从预处理的76个精度和可信度较高的地震事件中获取。山西地区震源深度范围为5~20km,分别绘制震源深度5、10、15、20km的理论“折合走时”,并将其与实测“折合走时”进行对比。首先对Pb震相进行对比分析(图 4),如图 4所示,随着康氏面的深度h1由18km逐渐增大到23km,理论“折合走时”由实测“折合走时”的下方逐渐上移至其上方,所以可以判断h1的波动范围为18~23km,平均值为20.5km。
|
图 4 Pb“折合走时” 实线表示不同震源深度条件下,Pb震相理论“折合走时”;空心圆点表示实测“折合走时” |
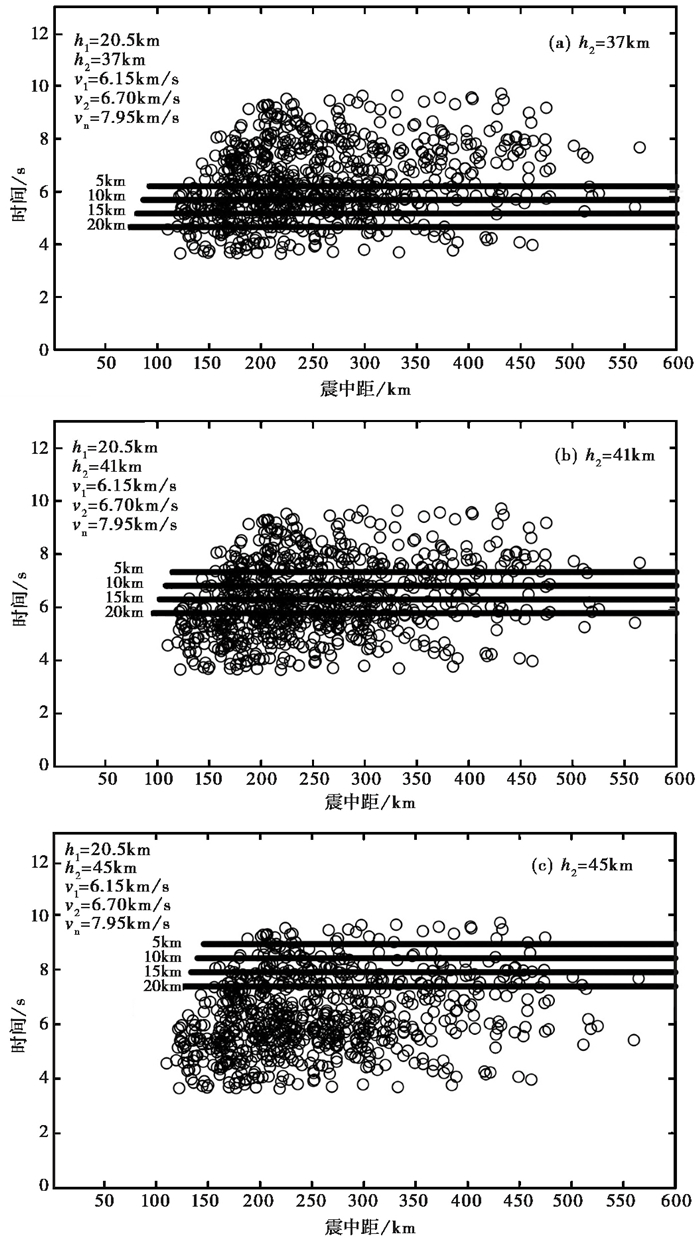
同样的方法,固定h1的值为20.5km,调整h2的深度对比Pn震相(图 5),如图 5所示,随着莫霍面的深度h2由37km逐渐增大到45km,理论“折合走时”由实测“折合走时”的下方逐渐上移至其上方,所以可以判断h2的波动范围为37~45km,平均值为41km。
|
图 5 Pn“折合走时” 实线表示不同震源深度条件下,Pn震相理论“折合走时”;空心圆点表示实测“折合走时” |
在确定模型参数的最终结果时,本文采用同一种定位方法、不同的速度模型批量定位同一组多个震中被台站包围较好的地震事件,不同的模型参数对应不同的残差。根据孙安辉等(2011)的观点,在观测走时准确的情况下残差主要受速度模型影响,残差越小说明计算理论走时所用的速度模型越接近真实的地壳结构。使用同一种定位方法是为了避免由于定位方法的不同引起残差值的不同;震中被台站包围较好地震事件的实测走时具有较高的精度和可信度。
根据确定的模型参数波动范围,分别组合得到多组模型,依次对所选地震采用Hyposat方法(Schweitzer,2001)进行批量定位、分别计算残差。为避免纵横波波速比不确定的因素引入过大误差,首先仅使用Pg、Pn震相进行批量定位计算,并分2步完成。第1步的模型参数滑动步长较大,速度值以0.1km/s、深度值以1km为步长,波动范围在前文确定的基础之上适当扩大。其中v1的取值范围为5.70~6.30km/s,v2的取值范围为6.50~6.90km/s,vn的取值范围为7.70~8.10km/s,康氏面深度h1的取值范围为19~23km,莫霍面深度h2的取值范围为35~45km。通过组合一共获得9625组模型,每一组模型都分别对所挑选的76个地震事件进行批量定位,共进行731500次计算。残差最小的一组速度模型见表 5。
| 表 5 Hyposat第1次计算残差最小的模型参数 |
第2步是在第1步运算的基础上进一步精细运算,缩小滑动步长和波动范围,其中v1的取值范围为6.10~6.25km/s,v2的取值范围为6.70~6.85km/s,vn的取值范围为7.85~8.00km/s,h1的取值范围为19~22km,h2的取值范围为38~43km,速度值以0.01km/s为步长,深度值以0.5km为步长,共获得36864组模型,残差最小的一组速度模型见表 6。
| 表 6 Hyposat第2次计算残差最小的模型参数 |
然后固定P波速度及康氏面、莫霍面深度,使用Sg和Sn震相确定S波的速度模型。由于通常情况地壳波速比为1.73,因此将vPg/vSg、vPb/vSb和vPn/vSn值的波动范围设定为1.65~1.80、步长为0.01进行批量定位。通过计算得出各个波速比对应的平均定位残差,残差最小的8组参数见表 7,当vPg/vSg=1.71、vPb/vSb=1.71、vPn/vSn=1.76时平均定位残差最小。
| 表 7 不同波速比对应的残差值 |
综合上述研究成果,可以得出山西地区地壳一维速度模型——山西2015地壳速度模型(表 8)。
| 表 8 山西2015地壳速度模型参数 |
为了检验山西2015地壳速度模型的适用性与准确性,采用批量定位比较残差、PTD测定深度和人工爆破等3种方法对山西2015地壳速度模型和修正J-B模型定位结果进行了比较。
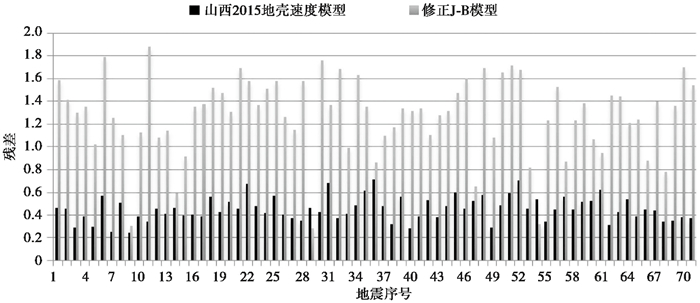
5.1 批量定位比较残差采用同样的定位方法和相同的地震事件,计算不同模型对应的定位残差值,残差值较小则说明该模型的适用性较好。批量定位的地震事件取自山西测震台网2015年1~7月统一编目结果,从中筛选ML≥2.0的71个地震。利用Hyposat程序针对2种速度模型进行了定位(图 6),由图 6可知,山西2015地壳速度模型的残差值远小于修正J-B模型的残差值。具体表现为:山西2015地壳速度模型的残差值波动范围为0.245~0.714,平均值为0.453,而修正J-B模型的残差值波动范围为0.282~1.849,平均值为1.183。
|
图 6 不同模型残差对比图 |
震源深度测定的确定性方法(简称PTD方法)是朱元清等(1990)在20世纪90年代提出的,该方法利用初至Pg、Pn震相比较清晰,莫霍界面的速度vn容易确定且较稳定的特点,并结合直达Pg波和折射Pn波的离源射线反向特征,能比较敏感地反映地震震源深度的变化。该方法可以在Pn到时震相转换时对不同台站进行组合,参与深度计算的组合数为(记录到Pg的台站数)×(记录到Pn的台站数)”。由于PTD方法对速度模型依赖性较高,速度模型的适用性程度与测得有效震源深度的个数成正相关,因此可以检验速度模型的适用性。
2010年6月5日山西阳曲发生MS4.6地震,这是近年来发生在山西地区震级最大、波及范围最广、震中被台站包围情况良好的地震事件。分别采用山西2015地壳速度模型和修正J-B模型利用PTD方法测定阳曲MS4.6地震的震源深度。其中,记录到Pg的台站数为25,记录到Pn的台站数为22,通过组合一共可以得到550个理论深度值。山西2015地壳速度模型中有效深度有457个(占83.1%),计算深度值为16.7km,与宋美琴等(2013)采用CAP方法反演的结果(17~20km)相近;而修正J-B模型的有效深度有111个(占20.2%),计算深度值为6.4km。由此可见,山西2015地壳速度模型相对修正J-B模型适用性较强。
5.3 人工爆破检验人工爆破有着具体的发震时刻和震中位置,因此在验证模型和算法等方面时其优点非常鲜明。本文分别采用2种模型测定2014年11月25日发生在山西中阳的人工爆破参数。经实地调查得知,该爆破发震时刻为15:35:13.0,震中坐标为37°25.2′N、111°12′E,震深0km。采用2种模型分别进行测定(表 9),与实际参数相比,不论震中位置还是发震时刻,山西2015地壳速度模型测定结果均优于修正J-B模型测定结果。
| 表 9 2种模型的测定结果 |
本文利用2009~2014年山西测震台网大量的实测震相数据开展了山西地区一维地壳速度模型的研究,并得到了以下结论:
(1) 得到的新的适合山西地区的一维地壳速度模型——山西2015地壳速度模型参数为:上地壳vP=6.18km/s,vS=3.62km/s,厚度21km;下地壳vP=6.79km/s,vS=3.97km/s,厚度20km;莫霍面vP=7.95km/s,vS=4.52km/s。
(2) 通过批量定位比较残差、PTD测定深度和人工爆破等3种方法检验皆证明,山西2015地壳速度模型相对修正J-B模型在山西地区地震定位过程中具有残差小、精度高和适用性强的特点。
(3) 山西2015地壳速度模型上地壳P波的传播速度为6.18km/s,显著高于修正J-B模型中的5.57km/s;而莫霍面P波的速度为7.95km/s,小于修正J-B模型中的8.01km/s。这可能与山西断陷盆地带在拉张过程中上层松散堆积层减薄而致上地幔密度小的物质上涌有关。
需要指出的是,山西2015地壳速度模型是针对山西全区的地壳速度模型,对于小区域台网,可参考本文给出的方法进行专门的探究。
致谢: 感谢山西省地震局、上海市地震局和全国一维速度模型工作组全体成员对本研究的大力支持和帮助,感谢匿名审稿人对论文修改提出的中肯的意见与建议。
陈向军、上官文明、宋秀青等, 2014, 新疆全区和分区地壳速度模型的分析, 中国地震, 30(2): 178-187. DOI:10.3969/j.issn.1001-4683.2014.02.005 |
邓晋福、苏尚国、赵海玲等, 2003, 华北地区燕山期岩石圈减薄的深部过程, 地学前缘, 10(3): 4-49. |
郭震、陈永顺、殷伟伟, 2015, 背景噪声面波与布拉格重力异常联合反演山西断陷带三维地壳结构, 地球物理学报, 58(3): 821-831. |
邱瑞照、邓晋福、周肃等, 2004, 华北地区岩石圈类型:地质与地球物理证据, 中国科学:D辑, 34(8): 698-711. |
宋美琴、李华玥、韩立波等, 2013, 用CAP方法反演2010年6月5日山西阳曲MS4.6地震震源机制解, 地震工程学报, 35(3): 692-697. DOI:10.3969/j.issn.1000-0844.2013.03.0692 |
宋美琴、郑勇、葛粲等, 2012, 山西地震带中小震精确位置及其显示的山西地震构造特征, 地球物理学报, 55(2): 513-525. |
孙安辉、陈棋福、陈颙等, 2011, 天山东北部地震的重新定位和一维地壳速度模型的改善, 中国地震, 27(3): 235-247. DOI:10.3969/j.issn.1001-4683.2011.03.003 |
魏文博、叶高峰、金胜等, 2007, 华北地区地壳P波三维速度结构, 地球科学(中国地质大学学报), 32(4): 441-451. |
徐扬、田勇、啜永清等, 1997, 大同-阳高6.1级震群震源区及其附近地区地壳三维P波速度结构反演, 山西地震, (1/2): 24-29. |
于利民、刁桂苓、李钦祖等, 1995, 由深源远震体波记录反演华北北部地壳上地幔速度结构, 华北地震科学, 13(3): 11-20. |
张健狮、祝治平、张先康等, 1997, 山西高原北部地壳上地幔地震波速结构与深部构造, 地震地质, 19(3): 220-226. |
张曼丽, 1994, 山西地区分区近震走时表的编制与检验, 内陆地震, 8(2): 109-117. |
张培震、邓起东、张国民等, 2003, 中国大陆的强震活动与活动地块, 中国科学, 33(增刊): 12-20. |
张学民、刁桂苓、束沛镒, 2004, 鄂尔多斯块体及其东南缘剪切波速度结构与波速比研究, 中国地震, 20(1): 53-63. DOI:10.3969/j.issn.1001-4683.2004.01.006 |
张学民、束沛镒、刁桂苓, 2003, 山西省部分台站下方S波速度结构研究及与地震关系探讨, 地震学报, 25(4): 341-350. DOI:10.3321/j.issn:0253-3782.2003.04.001 |
朱元清、石耀霖、李平, 1990, 一种确定地震深度的新方法, 地震地磁观测与研究, 11(2): 4-12. |
祝治平、张建狮等, 1999, 山西中南部壳幔结构的研究, 地震学报, 21(1): 42-49. DOI:10.3321/j.issn:0253-3782.1999.01.006 |
Jeffreys H, Bullen K E, 1940, Seismological tables, British Association for the Advancement of Science, London: Gray Milne Trust.
|
Schweitzer J, 2001, HYPOSAT~An enhanced routine to locate seismic events, Pure Appl Geophys, 158(1/2): 277-289. |