将地震活动能量作为随机场,采用自然正交函数(或称经验正交函数)展开方法进行分析,已有研究成果见杨明芝等(2004、2011、2012、2013、2017)、罗国富等(2005、2011a、2011b、2011c、2012、2014、2015、2016)、马禾青等(2012、2017)以及许晓庆等(2011)的文献。结果表明,地震活动能量场时间因子是大地震的一种有预测意义的长、中乃至短期异常指标。将地震活动能量作为一个随机场,进行自然正交函数展开,研究场的主要部分,即几个主要典型场的权重系数的变化,可能是寻找大震前地震活动异常,进而进行地震活动预测的一种有效途径。以往开展地震活动能量场研究时,往往是将震中附近的一个矩形区域网格化,或者是将沿构造带的区域用较小的矩形网格化(杨明芝等,2011)。在实际工作中发现,以其他形式划分区域网格能够提取地震活动能量典型场的时间因子曲线异常。事实上,地震在孕育过程中震源周围不同距离的地震活动性也可能会发生不同程度的变化,地震活动的某一随机变量会随着与孕震中心的距离不同而出现不同反映。为此,可以把地震活动能量场函数F看成是距离r的函数,研究该能量场随距离的变化情况。
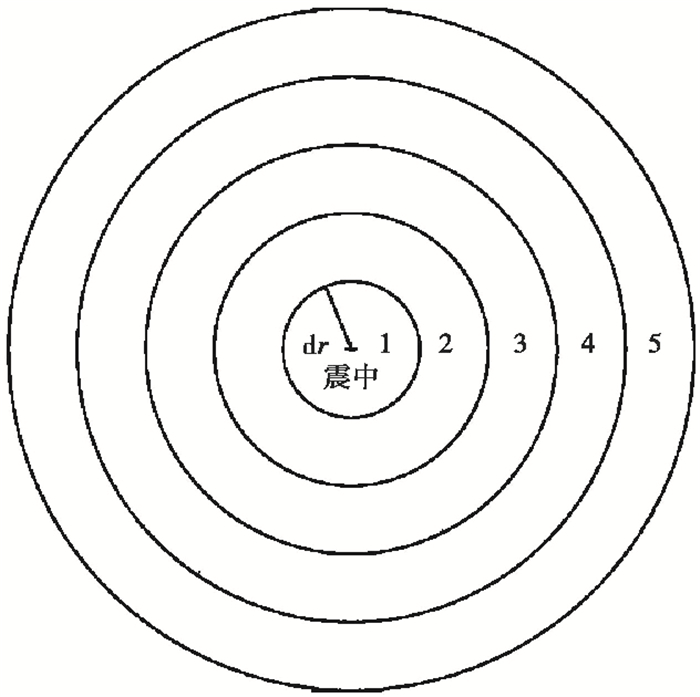
选择以震中为中心,以半径rn=n×dr向外扩展,形成半径dr的一个中心圆形区和n-1个环形带区域(图 1)。
|
图 1 环形区划分示意图 |
每个环形带的面积为π×(2n-1)×dr2,对这n个小环(圆)形区各时段的随机变量进行统计计算,并取单位面积平均值Fij,表示为矩阵形式
| $ \mathit{\boldsymbol{F}} = \left[ \begin{array}{l} {F_{11}}{F_{12}} \cdots {F_{1n}}\\ {F_{21}}{F_{22}} \cdots {F_{2n}}\\ \cdots \\ {F_{m1}}{F_{m2}} \cdots {F_{mn}} \end{array} \right] $ | (1) |
其中,Fij (i=1,2,…m;j=1,2,…n)为第j个环形带第i个时段单位面积随机变量的观测值或距平值。式(1)表示随机变量与距离r的函数关系,如果取随机变量为地震释放能量,式(1)就表示以时间t和空间距离r为自变量的能量场函数。
对式(1)进行自然正交函数展开,求解得到n个特征值和相应的特征向量,并计算时间权重系数(时间因子),由此分析场的时空分布特征及异常变化。关于能量场计算的理论方法,本文不拟赘述,可参考杨明芝等(2004)、罗国富等(2005)、马禾青等(2012)以及许晓庆等(2011)的文献。
以下将讨论环形带表示的地震活动能量场在大地震前的异常情况。
1 环形带能量场震例分析 1.1 7级地震震例取表 1所列的7次7级以上地震,研究时间段见表 1,取时间间隔为3个月,对资料进行时间离散化处理。以地震震中为中心划分环形区带,并进行能量统计(能量单位取1010J),计算时震级上下限取2.5≤ML≤5.5。取能量距平值,得到一个m×n阶的距平能量场矩阵函数。然后对其进行自然正交函数展开计算,求解协方差矩阵 R =F'F的n个特征值和相应的特征向量以及典型场的时间因子序列。
| 表 1 7次7级地震、研究时段和环形区能量场主要典型场的特征值、贡献率及异常情况 |
计算结果表明,7次地震均显示有异常变化。表 1给出了各次地震的环形带划分参数、主要典型场的特征值、贡献率及异常基本情况。
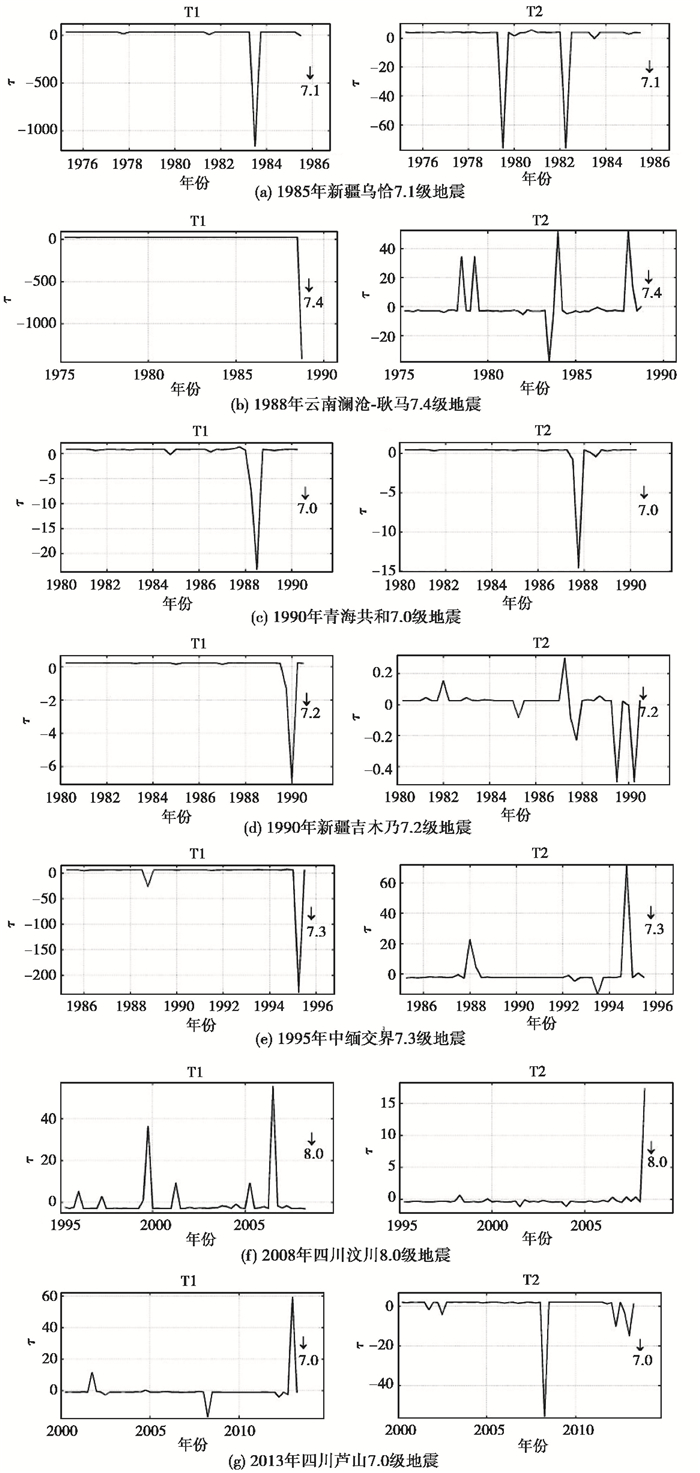
图 2是这7次地震环形带能量场时间因子曲线。由于这些地震环形带能量场的前2个典型场的拟合精度大多大于0.95(只有汶川地震为0.9414),因此只取前2个典型场就能够足以代表原始场,所以图 2中只给出了各次地震能量场的前2个典型场时间因子曲线。这2个典型场时间因子在震前3年内都出现了异常突跳变化,各次地震典型场出现异常的时间和突跳幅度在表 1中给出。以2008年汶川8.0级地震为例(图 2(f)),震中周围区域按dr=25km,划分成n=11个环形带,能量场的前2个典型场展开精度为0.9414。第1个典型场时间因子于2006年8~10月的点值出现幅值55.4310的突跳上升;第2个典型场时间因子于震前1.5~4个月,即2008年1~3月的点值出现幅值17.3285的突跳上升的短临异常。
|
图 2 7次7级以上地震环形区域能量场前2个典型场的时间因子曲线 “τ”指能量场典型场的时间因子,经过一系列计算得到,可看做为一无量纲量 |
因此,采用环形带能量场方法所得到的结果与在网格化区域得到的结论基本一致,同样可以用来分析大地震前的地震活动异常。
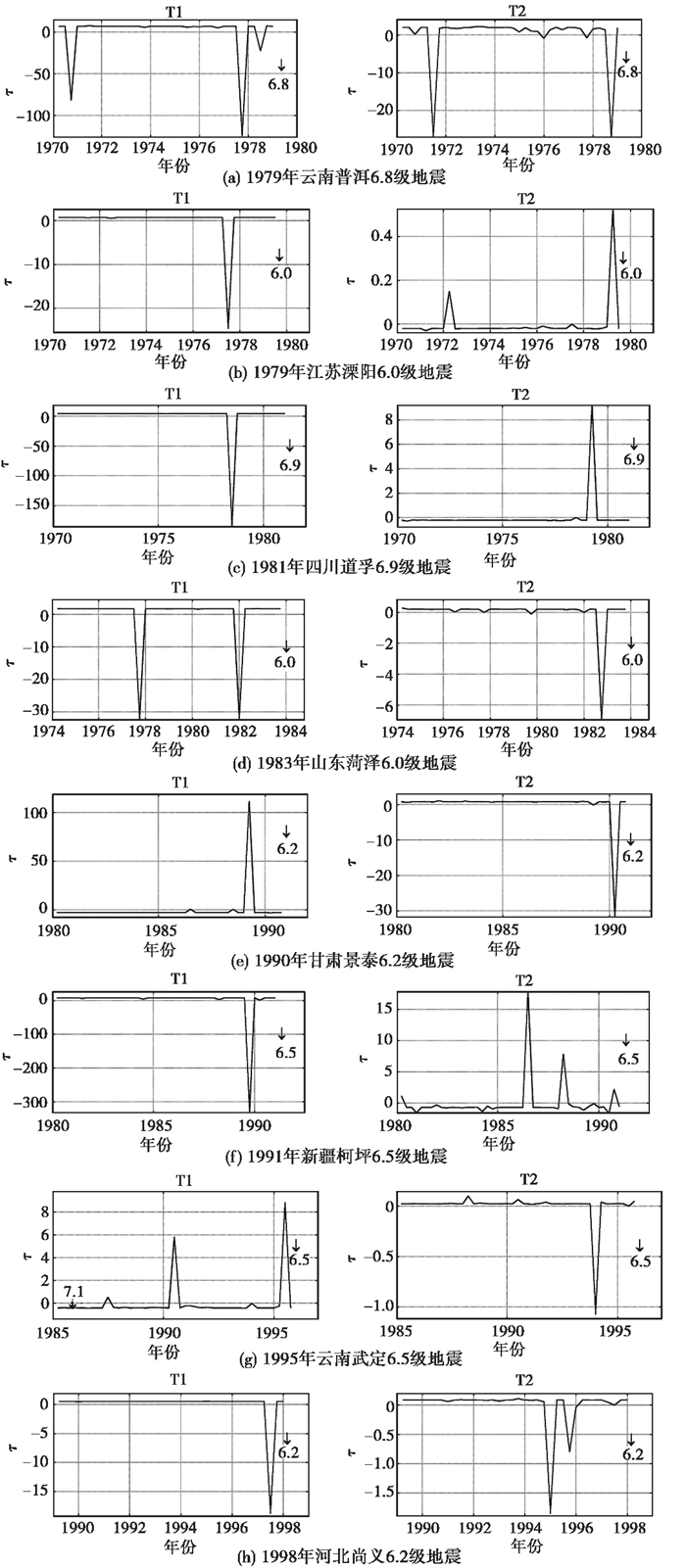
1.2 6级地震震例利用环形带能量场方法,研究了几次6级地震前环形带能量场的变化特征。表 2给出了这几次6级地震目录以及资料使用时段和正交展开的主要结果。可以看到,这几次6级地震环形带能量场展开的前2个典型场拟合精度都大于0.96,说明前2个典型场足以代表场的主要特征。表 2给出了各次地震前时间因子异常时间和幅度,以及发生异常的环形带编号,图 3是各次地震环形带能量场前2个典型场的时间因子曲线。可以看到,所研究的几次6级地震前,环形带能量场前2个典型场的时间因子曲线均出现了清晰的异常变化。
| 表 2 8次6级地震、研究时段和环形区能量场主要典型场的特征值、贡献率及异常情况 |
|
图 3 8次6级地震环形区域能量场前2个典型场的时间因子曲线 “τ”指能量场典型场的时间因子系经过一系列计算得到,可看做为一无量纲量 |
以类似于以往网格区域表示的能量场方法来分析环形带能量场异常的空间分布,表 1和表 2列出了各次地震环形带能量场主要典型场产生异常的主要环形带编号。下面以1988年11月6日云南澜沧-耿马7.4级地震和2008年5月12日四川汶川8.0级地震为例进行分析。
(1) 1988年11月6日云南澜沧-耿马7.6级地震。
该地震环形带能量场前2个典型场的分量值列于表 3。第1特征向量
| 表 3 云南澜沧-耿马7. 4级地震环带能量场前2个典型场的分量值 |
(2) 2008年5月12日四川汶川8.0级地震。
这次地震环形带能量场前2个典型场的分量值列于表 4。第1特征向量
| 表 4 汶川8. 0级地震环带能量场前2个典型场的分量值 |
通过对环形带能量场自然正交函数展开计算分析的结果表明,1988年云南澜沧-耿马7.6级地震活动异常主要分布在距震中约60km以内的近场区;2008年四川汶川8.0级地震的异常主要发生在距震中较远的225~250、150~175km两个环形带区域,而距离震中150km范围以内无异常显示,这些结果与以往通过区域网格化分析的结果一致(杨明芝等,2011、2012)。可见,无论是区域网格化方法还是划分环形带分析方法,自然正交函数展开分析都可以提取地震活动性异常变化,并且能够分析发生异常的空间分布情况。
3 结论和讨论(1) 采用环形带能量场方法所得到的结果与采用网格化区域得到的结果类似,都可以用来分析大地震前的地震活动异常。该结果表明,大地震前区域能量场发生改变揭示了地震孕育的某种本质,采用能量场分析方法能够发现其中的前兆信息,只要分析方法得当,分析手法细节的改变不会影响分析结果。
(2) 通过对环形带能量场自然正交函数展开计算分析的结果表明,环形带分析方法与区域网格化方法一样,不仅可以提取地震活动性异常变化,并且能够分析发生异常的空间分布情况。
(3) 在进行自然正交函数展开时,一般以震中为中心,选取一个适当的区域范围,选取时需要考虑区域内地震构造的分布及地震活动情况。梅世蓉等(1997)认为,7级地震前百余年的地震活动过程显示出活动水平较低、地震活动的强度和频度增大、地震活动减弱3个阶段特征。地震活动区长轴400~500km,并随着演变过程发展,地震活动区的分布面积逐步缩小,震前10年地震活动区为3°~4°的范围。在进行自然正交函数展开分析中,一般围绕震中选择经、纬度3°左右的范围作为研究区域,并根据地震震级、构造及地震活动分布等具体因素,做区域范围的适当调整。这样选择的区域大体包含了震前地震活动增强和减弱2个阶段的分布区域。
因此在选取环形区的中心点时,无论是选地震目录发布的“震中”位置,还是取震源区的中心位置,或是取破坏最重的位置,没有一定之规,只要研究区域范围合适,就能够得到较为理想的结果。
(4) 为了得到能量矩阵,要对区域进行环带划分。环带大小要使能量等值线能够反映出区域能量分布特征,环带划分过密,会使典型场代表的地震能量分布类型碎片化,不能突出场的主要特征。同时,会使协方差矩阵趋于退化,使收敛变慢。环带划分过稀,则不能很好地反映地震活动空间特征,使地震活动的空间差异性弱化,进而会失去一些重要的异常信息。环带划分还要考虑地震活动等因素,在选择环带参数时,要根据区域地震活动性的水平进行选择,环带大小要适中。笔者在计算时,根据地震分布往往就能够选择较为合适的dr,如果不合适,则再进行微调就能够选择出最合适的dr来。
(5) 如果所做研究是以分析地震异常为目的,在选择计算时间段时,一方面要考虑到场的平稳性对结果的影响,另一方面还要考虑地震活动异常的发展过程和特点。实际上,一次大地震从开始孕育到发生的时间并不十分清楚。马宗晋等(1990)在总结9大地震中得出,“在大震发生前的两三年观测到几种地震活动性异常”以及“在大震发生前两三年内,地震活动向近场区丛集”等特点,震前2~3年可能是地震活动异常活跃发生的时段。为此,通常选取震前10~15年作为研究时间窗,这样做既能识别出大地震前地震活动场出现的异常,又能呈现出地震活动相对平稳时段地震活动场的变化特点。
(6) 最后,讨论一下地震活动场方法用于实际强地震预测的可能性。在杨明芝等(2004、2011、2012、2013、2017)、罗国富等(2005、2011a、2011b、2011c、2012、2014、2015、2016)、马禾青等(2012、2017)以及许晓庆等(2011)的一系列成果中,作者提出了地震活动的随机场理论和地震活动异常的分析方法,并应用自然正交函数展开的方法分析了多次6级以上地震震例(杨明芝等,2013),证明随机场方法是分析地震活动异常的有效方法。但是,这些震例是在已知地震各种参数的情况下进行分析的。如何对未知大地震进行预测,仍然存在很大困难。
首先是关于地点预测问题。要对未知大地震进行预测,首先必须找到一个合适的研究区域或监视区域进行能量场分析。以往所分析的震例,震中位置和地震发生时间是已知的。知道了震中位置,就能够大体确定研究的区域范围。同时,还可以进行多方面的分析研究,了解区域地震活动情况和地震构造情况,然后对计算区域边界等参数进行调整。而地震发生时间已知,就可以大体确定计算时段。通过反复调整修订计算参数,达到较为满意的结果。但如果要预测未知大地震,确定地震发生的地点是一件十分困难的事情。为此,预测中可以借用动态追踪思路,即将年度确定的重点危险区经过适当调整作为研究的目标区,进行自然正交函数展开计算分析。为了取得较满意的结果,可同时选择几个目标区和不同的时间窗进行实验分析计算。根据预测地震所处区域环境和地震活动实际情况,确定应用自然正交函数展开分析计算中研究区域的大小、网格划分等构建场函数的必要参数。
其次是关于时间预测问题。根据能量场时间因子异常具有的特征,若在大约3年内,能量场的前4个典型场有3个以上典型场(包括第1典型场)出现异常变化,且异常典型场所占比重超过90%,说明距离大地震的发生已经不远了,应当注意短临异常的出现。每个大地震震前的地震活动表现差异很大,异常出现的时间各不相同。以往分析的30次6级以上地震能量场出现的时间因子异常(杨明芝等,2013),在前4个典型场中异常出现距离地震发生最近的时间作为这次地震异常显示最短时(以月为单位),发生在异常出现3个月内的地震有11次。可见,有短临震异常的地震约占36.7%,如果都能把握这些异常信息,应用随机场方法能够做出短期或短临预测的地震大约只有这个比例。本文分析的15次震例中,有7次震例的异常出现在震前3个月内,占46.7%。环形带地震活动能量场方法是否能够更好地提取短临异常,需要更多的震例支持。另外的地震不能做出短临预测,异常大多出现在震前3年内,需要利用其它前兆手段进行短临预测分析。
最后是关于震级问题。随机场方法还不能提供异常与震级之间的定量关系,只能给出初略的估计,7级以上地震和6级地震异常的表现特征基本相同。因此,如果发现区域能量场具备发生大地震的异常指标,以发生6级及以上地震的概率最大。
罗国富、马小军、马禾青等, 2015, 芦山7.0级地震区域地震活动能量场分析, 防灾减灾学报, 31(1): 54-58. |
罗国富、屠泓为、马禾青等, 2011c, 滇西北至滇南强震危险区地震活动能量场分析, 地震研究, 34(4): 285-291. |
罗国富、屠泓为、马禾青等, 2012, 甘东南至陕甘宁交界中强震危险区地震活动能量场时空特征, 西北地震学报, 34(2): 132-137. DOI:10.3969/j.issn.1000-0844.2012.02.0132 |
罗国富、屠泓为、许晓庆等, 2011a, 宁夏及邻区地震活动能量场时空变化特征, 高原地震, 23(3): 13-18. |
罗国富、屠泓为、曾宪伟等, 2016, 2014年云南景谷6.6级地震前后活动能量场分析, 地震, 36(3): 125-134. DOI:10.3969/j.issn.1000-3274.2016.03.013 |
罗国富、杨明芝, 2005, 云南地区地震活动能量场的时空分布特征, 中国地震, 21(3): 13-18. |
罗国富、杨明芝、马禾青等, 2011b, 汶川8.0级地震前地震活动能量场中短期异常, 地震, 31(3): 135-142. |
罗国富、曾宪伟、马禾青等, 2014, 岷县漳县6.6级地震前地震活动能量场分析, 地震工程学报, 36(2): 314-319. DOI:10.3969/j.issn.1000-0844.2014.02.0314 |
马禾青、杨明芝, 2012, 2010年青海玉树7.1级地震能量场研究, 地震研究, 35(4): 485-490. DOI:10.3969/j.issn.1000-0666.2012.04.007 |
马禾青、杨明芝, 2017, 地震活动多参数综合变量的异常分析方法——以青海两次7级地震为例, 地震, 37(4): 50-57. DOI:10.3969/j.issn.1000-3274.2017.04.005 |
马宗晋、傅征祥, 1990, 中期地震预报研究, 见: 美国地质调查局, 马丽等译, 地震中期预报的观测和物理基础, 北京: 地震出版社.
|
梅世蓉、薛艳、宋治平, 1997, 华北地区强震前地震活动长期演变过程的共性.见:国家地震局预测预防司, 地震短临预报的理论与方法, 北京: 地震出版社.
|
许晓庆、罗国富、马禾青等, 2011, 首都圈及邻近区域地震活动能量场研究, 华北地震科学, 29(4): 44-48. DOI:10.3969/j.issn.1003-1375.2011.04.008 |
杨明芝、马禾青, 2011, 汶川8.0级地震前沿龙门山断裂带能量场变化, 中国地震, 27(3): 260-267. DOI:10.3969/j.issn.1001-4683.2011.03.005 |
杨明芝、马禾青, 2012, 汶川8.0级地震区域地震能量场分析, 地球物理学进展, 27(3): 872-877. |
杨明芝、马禾青, 2013, 大地震前区域能量场的时间因子异常特征, 地震, 33(3): 107-115. |
杨明芝、马禾青、罗国富等, 2017, 中国大陆6级以上强震前的地震应变场研究, 地球物理学报, 60(10): 3804-3814. DOI:10.6038/cjg20171010 |
杨明芝、赵卫明, 2004, 宁夏及邻近地区地震活动能量场的统计分析, 地震学报, 26(5): 516-522. DOI:10.3321/j.issn:0253-3782.2004.05.008 |
 2018, Vol. 34
2018, Vol. 34


