自20世纪30年代Richter提出用地震仪记录测量地震震级以来,震级标度发展了地方性震级、面波震级、体波震级、矩震级和能量震级等多种震级。随着GPS观测技术发展,利用高频GPS记录的地动位移来测定地震震级也进入探索之中。
连续高频GPS观测可以直接得到地震引起的地面位移,其中包括了地震产生的永久位移和激发的弹性波场位移。它具有不限幅、对低频振动敏感、能够记录几赫兹到零频的地震波以及永久真实地面位移的特点。如果能用高频GPS观测记录形成一种震级标度,这种标度将包括了地震能量的绝大部分,是对震级标度的有益探索。
一个大地震通过2种方式释放能量,即断层附近的塑性变形能(包括摩擦生热能)和激发的半空间弹性波场能(陈运泰等,1997)。地震观测记录可以比较准确地反演出大地震的断层长度、断层面积和地震的平均位错量等静态震源参数,从而得到矩震级(陈运泰等,2004)。另一方面,矩震级反映的是震源的静态特性(赵仲和,2013),即地震的零频信息,而无法反映地震的有限频率的能量,也就无法反映地震的震感,从震源来讲实际上是没有反映出地震震源的破裂速度,而地震震源的破裂速度也是直接影响激发弹性波场强度的重要因素。
Crowell等(2013)利用5次地震GPS观测数据提出了包含震级大小、震源距、峰值地动位移PGD(peak ground displacement)三者关系的统计关系式。Fang等(2014)、陈娜等(2015)、顾铁等(2015)分别利用GPS获取的测站水平位移峰值验证了古登堡面波震级公式。Melgar等(2015)利用了MW5.9~9.1的10次地震事件GNSS数据的精密单点定位测量结果,对Crowell等(2013)提出的关系式进行了验证,并对实时震级计算过程进行了模拟。本文在前人工作的基础上,对高频GPS观测到的PGD与地震矩震级统计关系进行了重新构建,采用数字化方法获取Melgar等(2015)的数据并进行拟合,而后进行震例检验,并对相关的各种因素进行了探讨。
1 数据该研究需要大量的数据作为基础,而实际地震GPS观测数据仍然不足。首先,有GPS观测数据的地震很少,其次,GPS数据由于保密或管理原因,许多地区的GPS台站数据几乎收集不到,使得可以得到的数据更加缺少。为了充分利用资源,只能利用已经发表的文章中的数据或从中国大陆构造环境监测网络(简称陆态网)、国际公开GNSS数据网站(如SOPAC、UNAVCO)收集数据。
本文收集了2方面的数据,其一是从陆态网和国际开放的GNSS数据中心收集并筛选出8次地震事件共172个GPS测站的观测数据,其二是从Melgar等(2015)研究中通过数字化方法获得的10次地震事件共829条数据。2部分数据中有1个共同地震事件即El-Mayor MW7.18地震,但对应的GPS测站不完全相同。
1.1 原始记录动态解算得到PGD收集国内陆态网和国际公开的GPS观测数据时,我们采用了如下的数据筛选标准:①MW>5.5;②每次地震事件对应的GPS测站数据不少于5个台。根据这些要求,选出MW5.9~8.1共8次不同震源机制的地震事件相关的172个GPS站观测数据,采样频率1~5Hz,地震目录见表 1(地震事件目录来自中国地震信息网和美国地质调查局http://www.csi.ac.cn和美国地质调查局https://earthquake.usgs.gov)。
| 表 1 所选用的8次地震事件的信息列表 |
采用GAMIT/GLOBK10.6软件中的事后动态定位TRACK模块 ①,选用适当距离的高质量观测站作为参考站,对各台站GPS数据进行逐历元差分处理,获得测站坐标时序。人工识别地震波到时,以其前60s数据取平均值作为测站的初始位置,后续坐标减去初始位置,即得到测站的位移时间序列。按照以下公式从GPS测站的三分向位移时间序列中提取峰值地动位移(PGD)
①http://www-gpsg.mit.edu/~simongtgkdocs.html
| $ {\rm{PGD}} = \max \left[ {\sqrt {N{{(t)}^2} + E{{(t)}^2} + U{{(t)}^2}} } \right] $ | (1) |
其中,N(t)、E(t)和U(t)分别对应于NS向、EW向和垂直向的位移时间序列。
将不同测站的震源距、峰值地动位移对应的时刻绘制成地震走时表,检查和剔除PGD计算中明显存在问题的数据,最终获得包含测站名、矩震级、震源距和PGD信息的一组数据。
1.2 数字化文献数据Melgar等(2015)总结了前人的工作,并在全球收集了10个地震1321条GPS观测数据。我们采用数字化方式从其图中提取10个地震众多测站的PGD数据。由于图面的部分数据重叠,未能获取到全部数据,仅得到了829条数据,表 2为实际的数据获取情况。
| 表 2 Melgar等(2015)所使用数据提取情况列表 |
表 2表明,除东北近海MW9.09地震外(其总数为832个),其它震例几乎全部数字化。东北近海MW9.09地震数字化数据占总数字化数据的44.6%,从数据分析的角度来看,理想情况是每个地震的数据均匀分布,该地震几乎占了全部数据的一半,会影响后面的统计回归分析,所以在回归分析中需要对各数据进行加权处理。
综合笔者解算和数字化论文图中得到的数据,共得到17次地震事件1001条数据。
2 震级标度研究方法Crowell等(2013)提出了如下的峰值地动位移统计关系,描述了不同震级在近、中、远场的地震动衰减关系
| $ \lg {\rm{PGD}} = A + B{M_{\rm{W}}} + C{M_{\rm{w}}}\lg R $ | (2) |
式中,A、B、C为回归系数;MW为矩震级;R为震源距(单位为km);PGD的单位为cm。
Melgar等(2015)使用近年来发生的MW5.9~9.1的10次地震事件的资料拟合并验证了该关系式,得到系数:A=-4.434±0.141,B=1.047±0.022,C=-0.138±0.003。即
| $ \lg {\rm{PGD}} = - 4.434 + 1.047{M_{\rm{w}}} - 0.138{M_{\rm{w}}}\lg R $ | (3) |
在地震学中有地方性震级ML公式(陈运泰等,2004)和面波震级MS公式(刘瑞丰等,2015)
| $ {M_{\rm{L}}} = \lg F + 2.76\lg \Delta - 2.48,\;\;\;\;\;\;30{\rm{km}} \le \Delta \le 600{\rm{km}} $ | (4) |
式中,ML为地方性震级;Δ为震中距,单位为km;F为位移的最大振幅,单位mm。
| $ {M_{\rm{s}}} = \lg {\left({\frac{A}{T}} \right)_{\max }} + 1.66\lg \Delta + 3.5 $ | (5) |
式中,A和T分别为面波的振幅(μm)和周期(s);Δ为震中距(°)。
式(2)、(4)、式(5)可以构建震级、震源距和峰值地动位移的新关系式
| $ \lg {\rm{PGD}} = A + B{M_{\rm{w}}} + C{M_{\rm{w}}}\lg R + D\lg R $ | (6) |
回归公式(式(6))的系数求解时,从统计分析角度应该让各个地震在统计分析中占有相对均衡的权重,为此使用下式表示损失函数及加权方法
| $ \min \sum \omega \cdot \left| {{M_{\rm{W}}} - \frac{{\lg {\rm{PGD}} - A - D\lg R}}{{B + C\lg R}}} \right| $ | (7) |
| $ \omega = \frac{1}{{{{\left({{N_{{M_{\rm{W}}}}}} \right)}^{3/4}}}} $ | (8) |
式中,ω为权重;NMW表示数据所在地震事件中包含的PGD数据条数。
我们的目的是通过PGD、震源距去计算震级,因此损失函数采用式(7)。为了弱化异常数据的影响,损失函数采用L1范数最小化进行回归,式(8)为所采取的数据加权策略。通常一个地震事件中数据越多越好,但此次收集的不同地震的数据量差别很大,各地震数据量最少6条,最多370条,为了防止数据多的地震事件控制最后的结果,则要求数据量最多的地震和数据量最少的地震,其总权重之比不超过3倍。按照式(8)的加权方法,一个地震事件所有数据的总权重为(NMW)1/4,实际应用中设其总权重为(NMW)1/n,按照不同地震之间总权重之比不超过3倍的要求,则有(Nmax)1/n≤3(Nmin)1/n,即有n≥3.75,因而在本次计算中将n取值为4。此种加权方式保证了同一个地震中的数据权重相等,且各个地震事件数据所占权重相差不大。
结合Bootstrap自助法(Hall,1990),每次随机去除10%的数据,重复1000次回归过程,得到回归系数的估值与方差。
3 震级标度探讨与分析首先利用数字化数据,按构建的关系式(式(6))回归得到新的震级关系式。再加入新的地震数据检验新关系式的适用度,并与原Melgar公式相比较,进行了相关的震例检验。
3.1 新回归关系式及对比以新提出的统计关系式(式(6))为基础,采用式(7)的矩震级MW损失函数,式(8)的加权方法,按照上面所述方法,对数字化数据进行回归,得到的回归系数分别为A=-6.0196±0.1289,B=1.3142±0.0165,C=-0.2348±0.0068,D=-0.5533±0.0519。
则新构建的关系式可表述为
| $ \lg {\rm{PGD}} = - 6.0196 + 1.3142{M_{\rm{w}}} - 0.2348{M_{\rm{w}}}\lg R + 0.5533\lg R $ | (9) |
式中,R为震源距,单位为km;PGD单位为cm。
对比分析Melgar等(2015)的标度关系式的系数与新拟合关系的系数(表 3),可以得到:①DlgR是一个非常重要的项,是不可忽略的; ②新拟合关系式系数A、B的标准误差均小于Melgar公式的标准误差,系数C的标准误差略大。
| 表 3 拟合系数对比 |
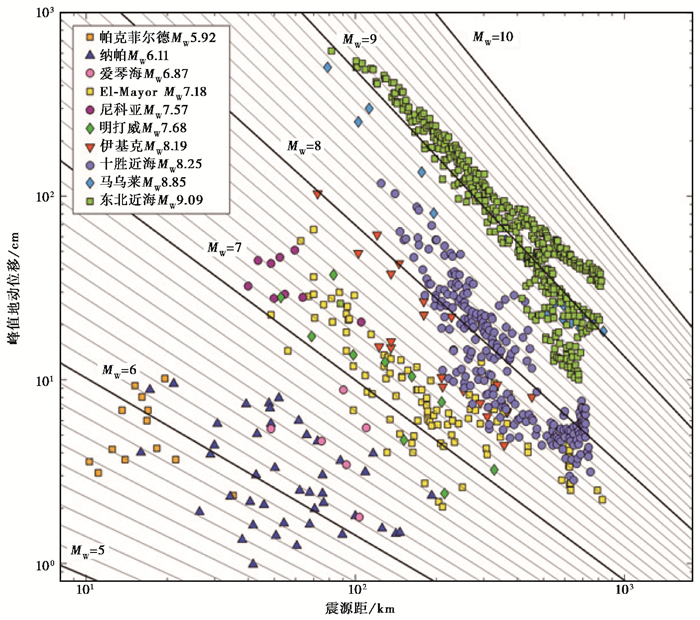
借鉴Melgar等(2015)的绘图方法,将数据与拟合的函数绘制在同一张图上,结果见图 1。由图 1可见,各个地震的震级分布与震级线较一致。
|
图 1 峰值地动位移的震级标度效果 斜线表示不同震级下预测的PGD随震源距变化关系;数据来源于数字化Melgar等(2015)的829条数据 |
与Melgar等(2015)建立的震级标度相比,图 1表现出震级标度线(等震级线)的斜率相对略大,则地震的PGD值在图 1中表现为:近距离PGD值对应于相对小的震级值,而远距离PGD值对应于相对大的震级值,这种情况与实际PGD值的震级表现更相符。例如:Melgar等(2015)的原图中,东北近海MW9.09地震PGD数据相对于实际的震级线出现了近震源“上抬”、远震源“下坠”的情况,震源距400km以内PGD数据比预测偏大,震源距400km以外PGD数据比预测偏小,数据分布的斜率与预测的震级线不符,类似的情况还出现在马乌莱MW8.85地震中;而图 1中,东北近海MW9.09地震的主要PGD数据前后段都较好地分布在震级线9.1附近,两者斜率较为一致,马乌莱MW8.85地震的PGD数据也在震级线8.8左右,两者对应的斜率较为一致。在低震级区域,本文和Melgar等(2015)结果表现非常一致,如帕克菲尔德MW5.92和纳帕MW6.11地震的PDG值在2种震级标度关系中都较好地分布在实际震级线附近。
3.2 震例检验将我们从GPS测站的原始记录解算的7个地震的PGD数据带入式(9)进行震级估算,表 4给出了每个地震震级估计统计结果。从表 4可以看出,对所有参加检验的地震,单个台站估计震级最大误差<1.0,最小偏差为0.01,平均震级差为0.31。如果不考虑墨西哥MW8.1地震的特殊场地效应,那么震级最大偏差为0.57。
| 表 4 新震例数据检验结果列表 |
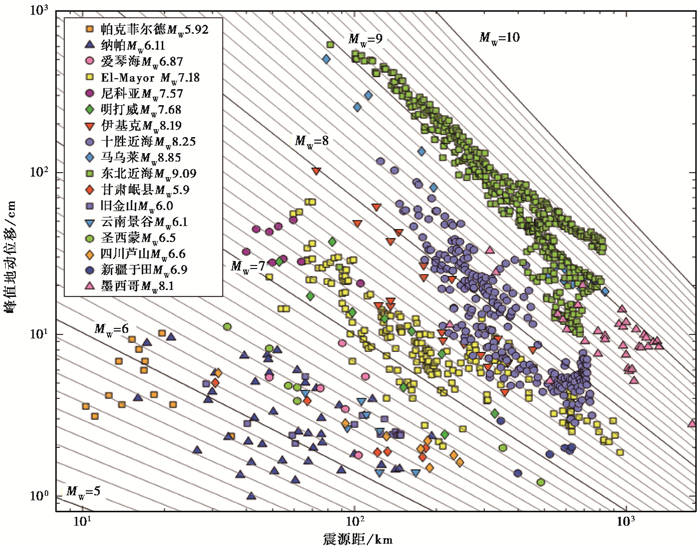
采用图 1的作图法将Melgar等(2015)的10个地震829条PGD数据和本文收集解算的8个地震172条PGD数据全部展绘在图 2中。从图 2和表 4可以看到,除墨西哥MW8.1地震明显高估外,其余地震震级估算大多数在0.5之内,仅个别偏差达到0.57。而等震级线较好地描绘了震级标度。
|
图 2 全部数据的峰值地动位移的震级标度效果 |
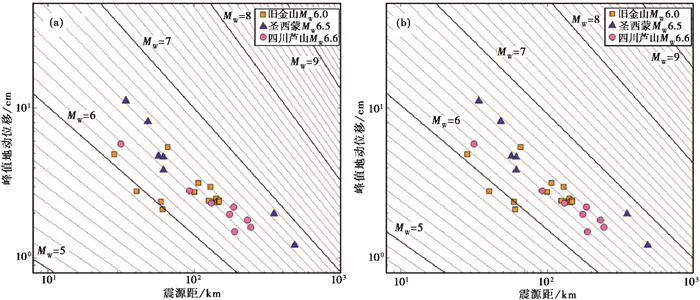
在拟合关系式(9)时较大地震的数据偏多,则从数据分析角度得知,较大地震的数据拟合应该效果更好,且在本文3.1中与Melgar等(2015)原图对比讨论中也得到证实。那么,这里验证主要考察式(9)对几个震级相对较小地震的震级估算情况。选取新数据中的旧金山MW6.0地震、圣西蒙MW6.5地震、四川芦山MW6.6地震3个事件,使用图 1的表示方法,将式(9)和3个地震事件的PGD数据展示在图 3(a)中,将Melgar等(2015)的关系式(3)和同样3个地震事件的PGD数据展示在图 3(b)中。由图 3可知,对于小地震,式(3)和(9)的效果较一致,只有当较远的距离或较大的PGD值时才能区分它们之间的差别。
|
图 3 小震级地震数据检验效果图 (a)新标度关系新震例数据检验图;(b)Melgar关系新震例数据检验图 |
综上所述,从原始数据我们得到统计残差相对更小的基于PGD的震级标度关系式(式(9)),较大地震PGD值分布更符合新拟合关系,较小地震PGD与震级估算检验也得到较好的结果,则可以认为在现有数据条件下,式(9)是一种可使用的PGD震级标度。
在拟合式(9)的过程中还发现,系数A、C、D尤其是C、D两个参数,小数点后第2位的变动也会较明显地影响PGD值的拟合效果,这说明拟合公式(式(9))的数据量严重不足。
4 讨论与分析进一步考察17个震例发现,除马乌莱MW8.85、明打威MW7.68地震和台站分散的帕克菲尔德MW5.92、纳帕MW6.11地震外,大部分不同程度出现GPS台站PGD值的分段现象,特别是测站丰富的东北近海MW9.09、十胜近海MW8.25、El-Mayor MW7.18地震,震例表现更加明显。
同时也发现,在图 2的左上部分不同地震GPS观测数据线性相对较好,右下部分不同地震GPS观测数据线性相对较差。结合GPS台站分布进一步考察PGD值的离散情况可以发现,一般在同一构造单元内PGD值线性度较好,而构造单元之间离散度较大。
4.1 震级标度公式的有效距离范围观察图 1、2可以看到,较远的台站的PGD值会出现分支、离散、分段变化等现象,一般震源距大则离散度大,而震源距小则离散度小。因此,震级标度的较稳定范围是距地震相对较近范围内的台站的记录。
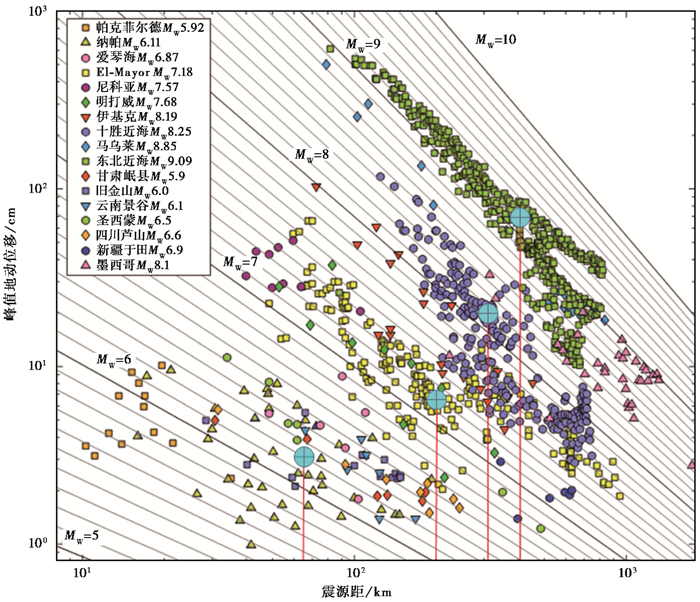
对于数据非常充分(不同距离都有丰富的台站)的3个地震(东北近海MW9.09、十胜近海MW8.25、El-Mayor MW7.18地震),如果将其PGD数据线性分布较好且不分叉的最远距离作为高频GPS计算震级的有效距离,如图 4中的EI-Mayor MW7.18地震,在200km附近2段数据出现不同线性分布,有效最远距离取分叉处为震源距200km,则取200km为该震级地震GPS估算震级的有效距离。同样方式取东北近海MW9.09地震的震级估算有效距离大约为405km,十胜近海MW8.25地震的震级估算有效距离大约为310km。
|
图 4 四个地震最远有效距离的取值情况 |
小地震事件离散性较高,也选取在不同距离上有台站而且具有误差较小线性段的地震(满足该条件的只有旧金山MW6.0地震)的最远距离,如图 4中的旧金山MW6.0地震,最远有效距离取值63km。
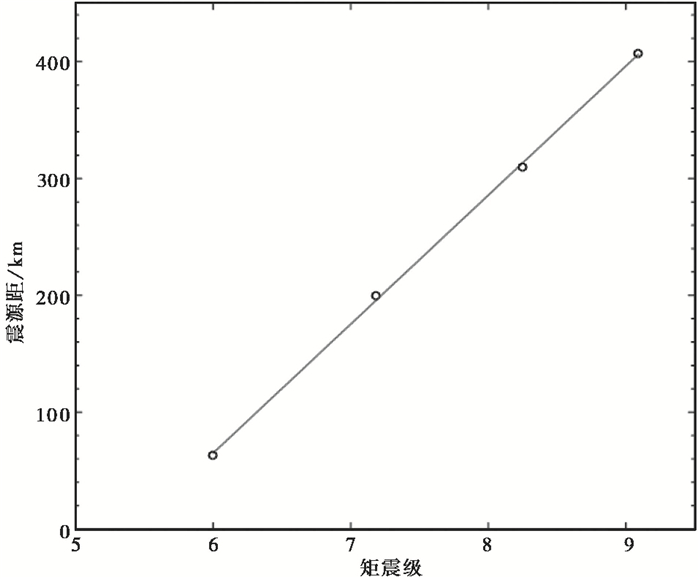
上述4个地震事件最远有效距离取值情况见图 4,其它线性较好的马乌莱MW8.85、伊基克MW8.19、明打威MW7.68、云南景谷MW6.1等地震均因其观测点稀疏而无法分辨最远有效距离。将这4个点进行线性拟合,线性表达式如下,拟合效果见图 5。
|
图 5 震级估计有效距离的拟合图 |
| $ {R_{\max }} = 112.2 \times \left({{M_{\rm{w}}} - 5.41} \right) $ | (10) |
图 5的直线说明:①这条直线下半部可以作为估算震级使用的台站范围,因为统计上讲这个区域震级和对应的距离内台站观测值会出现线性情况,有利于震级估算;②直线与横坐标的截距是5.41,也就是说,对于小于这个震级的地震,GPS观测不到。通过这2个认识得到了高频GPS用于估算震级的有效距离和可以观测到的地震的最小震级。
式(10)虽然是在较粗略的情况下得到的,但也的确揭示了图 2中左上半部PGD值分布线性较好,右下半部PGD值分布线性较差的内涵。
4.2 GPS适宜测定的震级范围观察图 2不难发现,对于大震级地震,通过GPS观测的PGD值计算震级,误差的变化范围为-0.4~0.4,例如东北近海MW9.09、十胜近海MW8.25、墨西哥MW8.1、依基克MW8.19、尼科亚MW7.57、明打威MW7.68地震等(图 4);而对于小地震,震级变化范围相对大,例如观测站比较丰富的帕克菲尔德MW5.92、纳帕MW6.11地震(图 4)。这说明GPS观测对测定大震级地震较适用。
在关系式(10)中得到直线的截距是5.41,也就是说,按照这个直线,可能观测到的地震最小震级为5.41。从图 2还可以看到地面位移为1cm的PGD值在整个图幅中只有1个点:纳帕MW6.11地震的震源距距离42km处有1个观测站,这是所收集实际观测资料中唯一一个1cm位移对应的距离值。而实际上GPS动态解算的精度一般为1cm,考虑GPS定位的绝对噪声基底(殷海涛等,2009),我们不能很好分辨1cm是位移还是误差。按照观测到2cm位移,如果在震源距20km处,根据式(9)可以得到震级为MW5.6。而根据式(10),同样得到对于MW5.6地震,最远的观测震源距为Rmax=21km。
综合上面讨论得出,GPS实时解算震源距20km处,可以观测到MW5.6及以上的地震。而Michel等(2017)通过在瑞士的GPS观测认为能够实现高频GPS记录MW5.6以上的地震,这符合我们的计算结果。综合以上结论,我们认为高频GPS至少能够记录MW5.6的地震。
4.3 地形、场地、传播路径和震源机制对震级的影响GPS观测得到的地面位移不仅与地震大小、震源距有关,同时与地震震源机制、破裂过程、地震波传播的路径、GPS观测站所处的构造单元(如盆地、海湾等)的场地情况、台站相对于高程、天线杆的高度等因素有关(董娣,2006)。
首先从GPS台站分布及震源相对位置来看,从图 2中发现了PGD值分段、离散的现象。东北近海MW9.09地震在震源距约400km处,PGD出现了3个分支,其一为北海道的台站记录,其二为东京以南的台站记录,其三为与震源平行的台站,可能是受震源破裂特性的影响,3部分数据分支的原因都与震源及其区域的地形、地质结构差异有关。
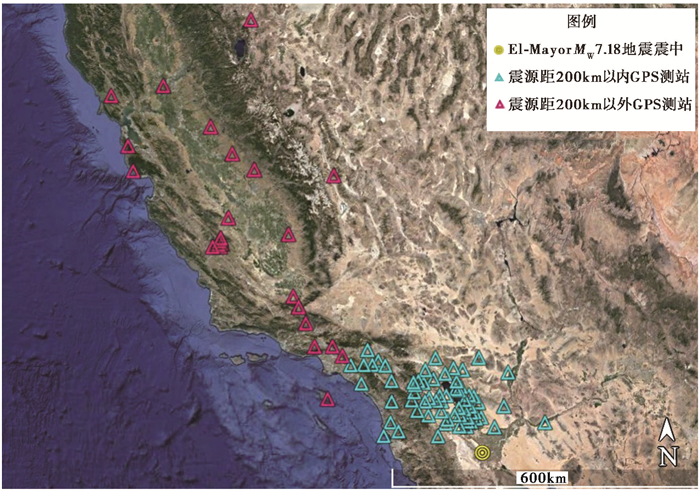
同样情况出现在其他地震中。如EI-Mayor MW7.18地震,在震源距约200km,数据前后分成2段线性分布,对应的理论震级相差约0.3。对照地形图(图 6)发现,所有测站基本处于震源的西北方向,但震源距200km以外和200km以内的测站地形差异明显,前者大多处在一个构造单元内(图 6中浅蓝色三角),其PGD值在图 2中显示出大约以MW7.2震级线为中心分布;后者出现在盆地边缘或另一个构造盆地(图 6中红色三角),红色三角PGD值在图 2中展示出大约在以MW7.6为中心的震级线上,这种地形对PGD有明显放大作用。
|
图 6 EI-Mayor MW7.18地震GPS测站分布 背景图片来自Google-Earth |
旧金山MW6.0地震,单个台站估算震级最大误差<0.51,最小偏差为0.02,平均估算震级为6.34,比其矩震级大0.34。图 3清楚展示其测站数据出现分段现象,较近的4个GPS测站在震级估算和线性分布上都有较好表现,这4个GPS测站获取的PGD进行震级估算为MW6.01,震级与实际偏差为0.01,其他大多数测站距离较远,震源距大于70km,震级估值偏差也相对较大,大约为0.44。而且这些GPS测站多处于沿海和盆地边缘,PGD数据可能受这些场地因素、传播路径等综合的放大作用,从而使远距离台站出现相对较大的PGD值。
对于圣西蒙MW6.5地震,数据也出现分段现象。在震源距100km以内的NEE方向5个台站,震级估算为MW6.3~6.5,接近实际矩震级;EN方向300km以外的2个数据估算的震级为6.7~6.9(图 3中可直接得出)。参考地理位置和周边地形,可以发现震源和100km内的5个GPS测站处于同一构造单元,300km以外的2个测站处于另一个构造单元(较远的测站作为参考站)。
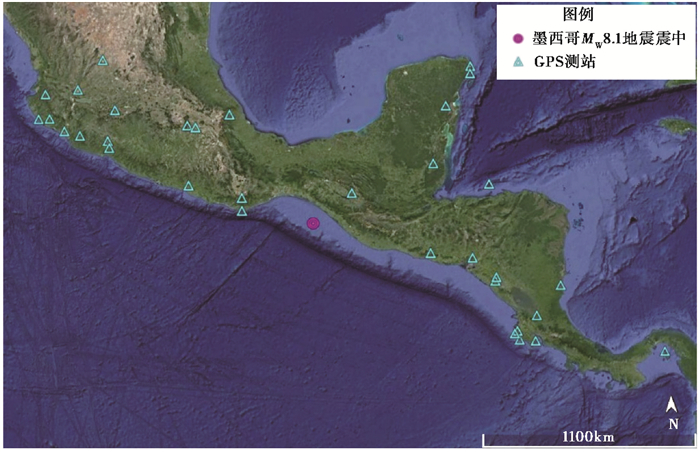
墨西哥MW8.1地震,PGD普遍偏大,其平均震级估值偏大0.55,单测站最大震级估值偏大0.91,几乎为全部样本的最大震级偏差值。图 7为记录墨西哥MW8.1地震的GPS台站分布图。图 7显示,该地震的GPS测站几乎都在海边,仅6个测站可以勉强算内陆,海岸、海湾地形放大了台站的PGD值,而且台站分布在地震震中的三个象限内,震源机制的效应也使台站PGD值离散。
|
图 7 记录墨西哥MW8.1地震的GPS台站分布 |
场地、地形因素对于GPS观测获得的PGD的影响是不可避免的。而另一方面,震源对各个方位的台站会有不同的辐射效应,而不同震源类型和震源位置会使得同一台站的辐射效应产生差异。可见震源也是影响一个台站观测值的重要因素(Lee et al,2009)。所以,对所拟合的震级关系式(式(9)),需要考虑这2个影响因素。设场地放大倍数为S,震源辐射影响倍数为为 F,则式(9)可以扩展为
| $ \lg {\rm{PGD}} = - 6.0196 + 1.3142{M_{\rm{w}}} - 0.2348{{\rm{M}}_{\rm{W}}}\lg R + 0.5533\lg R + \lg S + \lg F $ | (11) |
如何测定S值实际上也是工程地震中的热点研究问题,而如何确定震源机制影响可以利用地震学方法进行进一步研究。
5 结论本文构建了普适度更广泛的地动位移标度关系式(式(9)),通过实际数据拟合发现PGD与lgR项的关联不可忽视;分析PGD数据在数据拟合中的分布情况后,得出基于高频GPS的PGD震级标度关系适合于震级大于MW5.6地震的震级估算;通过式(9)可以得出GPS适合于观测MW5.6以上地震。本研究还发现在用GPS的PGD值估算震级时存在一定的适用距离范围,由式(10)给出了最远适合距离的公式。此外,在结合实际数据的空间分布讨论的基础上,本文提出在震级关系式中分别使用校正值lgS和lgF作为每个测站的场地环境校正值和震源校正值。
经过各种检验可以得到:①利用GDP来估算震级,误差基本可以控制在1.0之内(无论是平均震级还是最大震级);②最好利用处于各个方位角台站的平均值来估算震级;③台站的场地、所处的构造单元都会带给震级估算引入误差;④在利用GPS观测的PGD来估算震级时,震源机制辐射花样和射线路径也是影响精确度的重要因素;⑤与测震台站相比,利用近距离GPS台站来估算震级较为准确。
陈娜、龚涛、李萌等, 2015, 利用高频GPS反演强震面波震级的最优适用范围探讨, 大地测量与地球动力学, 35(3): 512-516. |
陈运泰、刘瑞丰, 2004, 地震的震级, 地震地磁观测与研究, 25(6): 1-12. DOI:10.3969/j.issn.1003-3246.2004.06.001 |
陈运泰、吴忠良、李世愚, 1997, 世纪之交我国震源物理研究的进展与展望, 地球物理学报, 40(增刊I): 164-176. |
董娣, 2006, 地震动特性的影响因素与不确定性分析, 博士学位论文, 北京: 北京工业大学。 |
顾铁、李萌、陈聪等, 2015, 基于高频GPS位移时序的芦山地震特性分析, 科学技术与工程, 15(16): 128-133. DOI:10.3969/j.issn.1671-1815.2015.16.022 |
刘瑞丰、陈运泰、任枭等, 2015, 震级的测定, 4~62, 北京: 地震出版社.
|
殷海涛、甘卫军、肖根如等, 2009, 利用高频GPS技术进行强震地面运动监测的研究进展, 地球物理学进展, 24(6): 2012-2019. DOI:10.3969/j.issn.1004-2903.2009.06.011 |
赵仲和, 2013, 关于震级标度的讨论, 国际地震动态, (2): 16-20. DOI:10.3969/j.issn.0235-4975.2013.02.006 |
Crowell B W, Melgar D, Bock Y, et al, 2013, Earthquake magnitude scaling using seismogeodetic data, Geophys Res Lett, 40(23): 6089-6094. DOI:10.1002/2013GL058391 |
Fang R X, Shi C, Song W W, et al, 2014, Determination of earthquake magnitude using GPS displacement waveforms from real-time precise point positioning, Geophys J Int, 196(1): 461-472. DOI:10.1093/gji/ggt378 |
Hall P, 1990, Using the bootstrap to estimate mean squared error and select smoothing parameter in nonparametric problems, J Multivar Anal, 32(2): 177-203. |
Lee S J, Komatitsch D, Huang B S, et al, 2009, Effects of topography on seismic-wave propagation:An example from northern Taiwan, Bull Seismol Soc Am, 99(1): 314-325. DOI:10.1785/0120080020 |
Melgar D, Crowell B W, Geng J H, et al, 2015, Earthquake magnitude calculation without saturation from the scaling of peak ground displacement, Geophys Res Lett, 42(13): 5197-5205. DOI:10.1002/2015GL064278 |
Michel C, Kelevitz K, Houlié N, et al, 2017, The potential of high-rate GPS for strong ground motion assessment, Bull Seismol Soc Am, 107(4): 1849-1859. |
 2019, Vol. 35
2019, Vol. 35



