Analysis for Self-noise Level of the Very Broadband Seismometer Using Probability Statistic
0 引言
宽频带地震计凭借其观测频带宽、自噪声水平相对较低以及观测动态范围大等优势, 被广泛应用于测震台网的日常观测当中(Sleeman et al,2006)。测震台网中所使用的宽频带地震计种类很多, 其中有360s至5~50Hz对地速度平坦的超宽带地震计(KS54000、JCZ、STS1、CMG-1T、Trillium-360等)、120s至40Hz对地速度平坦的甚宽带地震计(STS2.5、BBVS120、CMG-3T、CTS-1EF、CTS-1、STS2、KS2000、Trillium-120、TDV-120VB等)、60s至40Hz对地速度平坦的宽频带地震计(BBVS60、CMG-3ESPC、TDV-60B等)以及20s或30s到40Hz对地速度平坦的宽频带地震计(FBS-3B、CMG-40T)。
衡量宽频带地震计观测能力的性能指标很多, 其中自噪声水平反映的是地震计在不同频段上能观测到的最小信号, 与地震计的限幅电平共同决定了地震计的“运行区间”(Evans et al,2010)。这个“运行区间”所覆盖的频率及取值范围很大程度上决定了该型号地震计的可用性及其适用的应用领域。
对于地震计自噪声的计算, Holcomb(1989)提出两台法, Sleeman等(2006)提出三台法, 这2种方法都是对多台套地震计同台址同时段固定长度的观测记录进行分析, 在假定地震计自噪声水平低于台基背景噪声水平的前提下, 认为观测记录中地震计拾取的地动信号是相关的, 而不同地震计间的自噪声是互不相关的, 利用相关性分析, 就可以从观测记录中扣除相关的地动信号而保留下不相关的地震计自噪声, 并以此给出地震计各个分向自噪声水平在频域上的展布形态, 通常以功率谱密度或是对应的分贝值来表示地震计自噪声水平的结果。
地震计自噪声水平的估算结果受到一些因素的影响, 有些是算法造成的, 如Holcomb(1990)指出, 在应用两台法测定地震计自噪声的过程中, 当2台地震计的仪器响应不同时, 错误的地震计传递函数会导致地震计自噪声水平估计结果出现较大误差;Li Xaiojun等(2015)指出自噪声算法中用于功率谱计算的参数组合变化同样会导致自噪声计算结果的较大差异;Hutt等(2010)指出, 在信噪比高于12dB的情况下, 三台法测定地震计自噪声的结果通常会比两台法的结果低一些。除此之外, 还有一些与外界环境、安装水平及方法有关, 如Hutt等(2010)指出, 地震计的供电设备干扰会造成地震计自噪声水平的升高;Holcomb(1990)指出同址比测地震计在安装方位上的较小不一致会导致自噪声估计的较大偏差, 这样的情况在0.1~1.0Hz频段上表现得尤为明显(Ringler et al,2011);Ringler等(2011)还指出, 地震计间的性能及安装方式差异同样会造成自噪声水平估计的结果变化。
还有一些影响来自于计算过程中的参数设置差异。在地震计自噪声水平的计算过程中, 通常采用Welch(1967)的平均周期图法计算功率谱密度(PSD:power spectrum density)。该方法将有限长度的数据分成多个互相重叠的数据段, 对数据加窗, 计算了重叠数据段的修正周期图, 然后对周期图结果求平均值来获得功率谱密度的估计, 其中有几个常用参数, 如加窗类型、加窗长度、分段数据长度及相邻数据段重叠率等, Welch(1967)已就加窗类型给出了2种选择, 并就其对功率谱估计的影响进行了一定分析。相关研究显示, 信号谱的计算精度与分段数据的长度成反比, 在没有重叠的时候, 平方相关系数的偏差及方差与数据分段的个数成反比(Welch, 1967;Carter et al,1973;Ringler et al,2011), 随着数据长度的增加(Oppenheim et al,1978)和重叠率的增大(Ringler et al,2011), 谱计算的方差会降低, 不同数据段互相关性及稳定性会增加, 但是相应的计算量也会增大。Carter等(1973)指出, 在固定窗口的时候, 当重叠率达到一定程度后, 数据段互相关性及稳定性会达到一个相对恒定的状态。这些参数的不同组合在信号自功率谱、互功率谱及平方相关系数计算结果中产生的差异会影响到地震计自噪声水平的计算结果。
为了保证地震计自噪声水平算法的稳定性及计算结果的可比性, Evans等(2010)及Ringler等(2011)针对地震计噪声水平的计算方法及流程提出了标准化, 并对参与计算的观测记录长度、加窗方法及采样率等参数进行了规定与分析。李小军等(2015)对地震计自噪声计算过程中功率谱计算参数的合理选取进行了重点论述, 指出即便是在数据、算法及流程都相同的情况下, 使用不同的计算参数所得到的地震计自噪声水平值并不一致, 但整体具有一定规律性, 即整体趋势是随着K线的增加而降低, 并在窗口长度98%及重叠率98%时达到最小值, 整体最大差异达到20dB以上, 并根据自噪声计算结果的方差及偏差给出了推荐参数组合。
上述研究对统一地震计自噪声计算流程、评价地震计观测能力下限及判断不同型号地震计的应用领域均起到了较好的作用。但与此同时, 目前对地震计自噪声水平随时间变化的规律研究并不充分。Ekström等(2006)和Davis等(2007)的研究表明宽频带地震计的参数如增益水平还会随着时间的推移而变化, 这样的规律已经由更早的实验证明(Yuki et al,2002)。地震计的自噪声水平也应该是随着时间推移在频域按照一定变化规律在一定区间分布的, 并且这种分布是非均匀的, 因此, 仅以给定时段内一定长度观测记录的分析结果作为某个型号地震计自噪声水平的表征并不能充分描述其特性。
Sleeman等(2012)参考应用概率统计分析地震台站背景噪声的方法(Mc Namara et al,2004), 提出使用概率统计的方法对地震计的自噪声水平进行分析。Sleeman等(2012)分别在未加保温罩及加装保温罩的情况下, 利用长时间的同址观测数据计算地震自噪声, 剔除了结果中超过模型30dB的结果, 给出了不同频点上地震计噪声水平的概率密度分布, 以最高概率对应的噪声水平构建噪声模型, 并分别与均值及Ringler等(2010b)给出的同型号地震计自噪声水平模型进行比较, 分析了差异及其来源。值得注意的是, Sleeman等(2012)给出的结果中, 相对高概率所对应的自噪声值都集中在1个条带内, 但概率差异并不超过1个数量级, 也就是说其用于建立噪声模式的自噪声值的概率只是大于而并非明显高于前面所提条带内其他值所对应的概率。
基于以上研究, 本文应用三台法对3套测震仪器连续1000hr的同址观测垂直向数据进行计算以获取地震计自噪声的样本, 提出分频带概率统计法来分析地震计自噪声, 该方法将自噪声在窄带的特征信息反映到中心频点上, 再通过概率统计将概率上具备跨数量级优势的典型自噪声值提取出来, 获取了与频点一一对应且具有统计意义的自噪声水平值, 有助于建立地震计自噪声水平的数学数值建模, 通过与单小时众值法及单频点概率统计法的比较, 为地震计自噪声水平测试建标提供参考。
1 自噪声计算方法及实验
1.1 计算方法
通过同址观测计算地震计自噪声的方法主要有两台法(Holcomb, 1989)和三台法(Sleeman et al,2006), 两台法的算法如下(Holcomb, 1989)
|
$
{N_{ii}} = \frac{1}{{|H{|^2}}}\left({{P_{ii}} - {P_{ij}}} \right) = \frac{{{P_{ii}}}}{{|H{|^2}}}\left({1 - {C_{ij}}} \right)
$
|
(1) |
式中, i,j=1,2, 3, ……且i≠j;Nii为第i个地震计的自噪声功率谱;Pii为第i个地震计的自功率谱;Pij为第i个与第j个地震计的互功率谱;Cij为第i个与第j个地震计的互相关系数。在两台法测地震计自噪声的过程中, 由于是在假设传递函数精确可知的前提下进行, 所以当2个地震计的传递函数出现较小的偏差时也会导致相对较大的噪声水平计算误差(Holcomb, 1990)。
三台法的算法如下(Sleeman等, 2006)
|
$
{N_{ii}} = {P_{ii}} - {P_{ij}} \cdot \frac{{{P_{ik}}}}{{{P_{jk}}}}
$
|
(2) |
式中, i,j,k=1,2,3, ……且i≠j≠k;Nii为第i个地震计的自噪声功率谱;Pii为第i个地震计的自功率谱;Pij为第i个与第j个地震计的互功率谱;Pik为第i个与第k个地震计的互功率谱;Pjk为第j个与第k个地震计的互功率谱。从公式(2)中可以看出, 在多引入1台地震计参与自噪声计算的前提下, 使用Pik/Pjk作为地震计i和地震计j间的相对传递函数可以降低计算结果对地震计传递函数的依赖(Ringler et al,2014)。
基于三台法受地震计传递函数影响相对较小的考虑, 本文在地震计自噪声的计算中全部采用三台法。
1.2 实验
本文使用山东马陵山国家地震仪器比测基地采购的3套Q330HRS六通道数据采集器和STS2.5甚宽频带地震计作为测试仪器组合, 该仪器组合也是IRIS及GSN很多地表型台站的测震观测专业仪器。
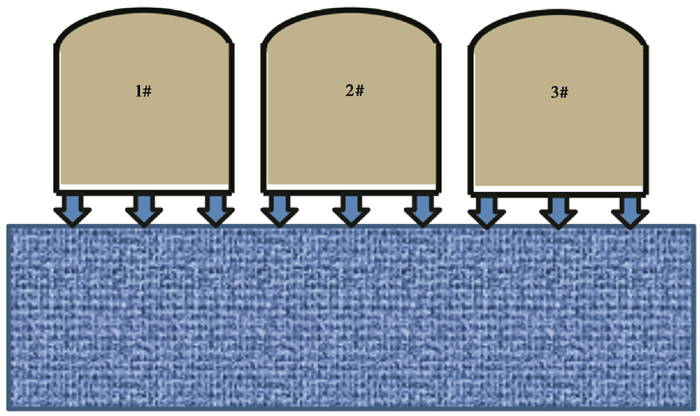
实验的场地位于山东马陵山地震台观测山洞13号洞室的1号摆墩上, 该摆墩为基岩上浇筑的水泥墩(长4.2m, 宽2.1m)。3台地震计的安装示意图如图 1, 安装位置尽量靠近且方位一致, 这样既可以减少由摆墩局部形变导致的重力耦合入个别地震计某些分向的现象, 还可以让3台地震计都处于可分辨信号的十分之一个波长内(Ringler et al,2011), 以达到保证3台地震计都可以拾取相同的输入地动信号的目的。3台地震计的方位由机械陀螺寻北仪进行校准, 每台地震计都通过摆线连接至数据采集器的前3个通道, 数据采集器全部使用GPS授时, 3套观测仪器的部分参数见表 1。
表 1

表 1 实验仪器参数表
| 序号 |
数采型号及序号 |
数采转换因子V/count |
地震计型号及序号 |
电压灵敏度(V/m·s-1) |
| 1 |
Q330HRS-6305 |
5.96e-7 |
STS2.5-150322 |
1500 |
| 2 |
Q330HRS-6302 |
5.96e-7 |
STS2.5-150321 |
1500 |
| 3 |
Q330HRS-6308 |
5.96e-7 |
STS2.5-150323 |
1500 |
|
表 1 实验仪器参数表
|
2 自噪声分析方法
对利用三台法得到的连续1000hr的垂直向自噪声计算结果分别采用单小时结果众值法、单频点概率统计法及分频带概率统计法等3种不同的方法进行对比分析。
2.1 单小时结果众值法
采用连续1000hr的观测记录, 对每个整小时的观测记录进行自噪声计算, 将每台地震计的1000条自噪声水平结果全部画到一张图上以众值的方式进行展示。可以得到地震计自噪声每个小时的形态, 堆叠的方式使得明显异常的结果不至于被掩盖, 便于一般性的归纳自噪声水平分布的特征, 分析共性与差异产生的原因, 结果见图 2。
2.2 单频点概率统计法
参考已有研究使用概率统计分析背景噪声(Mc Namara et al,2004;廖诗荣等, 2008)及地震计自噪声水平的方法(Sleeman et al,2012), 应用概率统计的方法对每台地震计的1000条自噪声水平计算结果进行分析, 按照计算频率点依据下式逐个进行统计, 用该频点上固定噪声水平数值出现的概率表征噪声水平分布情况, 得到的结果如图 3。单频点概率统计的方法事实上反映了在该频点上某个具有一定不确定度的固定值的聚集程度, 也可以理解为该固定值出现的权值, 目的是为了获取结果中优势值的分布区间
|
$
P{r_{ij}} = \frac{{{A_{ij}}}}{{1000}} \times 100\%
$
|
(3) |
在0.001~20.480Hz的频率范围内确立7182个频率点, 式(3)中的i对应的就是频率点的序号, i=1,……,7182, 步长为1;在-245dB~-90dB的区间确立156个噪声水平值, 式(3)中的j对应的就是噪声水平值, j=-245,……,-90;Aij表示在第i个频率点、自噪声水平为jdB的地震计自噪声计算结果的个数;Prij表示在第i个频率点、自噪声水平为jdB的地震计自噪声计算结果出现的概率;A代表数量(amount);Pr代表概率(probability)。
2.3 分频带概率统计法
本文参考已有研究使用概率统计分析地震台站背景噪声的方法(McNamara et al,2004;廖诗荣等, 2008), 基于单小时结果众值法中得到的1000条自噪声结果, 提出了先划分频带再进行统计分析的方法。先按照三分之一倍频程在0.001s~20.48Hz间划出43个子频带, 每个子频带中心频点的确定见下式, 对每条自噪声结果按照子频带划分以一个倍频程进行平滑(Mc Namara et al,2004), 得到每条自噪声结果43个中心频点上的噪声水平, 再对1000条结果进行概率统计分析, 结果见图 4。
要建立地震计自噪声水平的数学模型, 需要获得与频点对应的自噪声水平典型值, 我们认为这样的典型值与其他非典型值在概率上应该具有显著的差异, 而这样的差异应该是跨数量级的。鉴于这个原因, 分频带概率统计法基于单小时众值法中的结果,先将子频带内的自噪声窄带信息进行一次整合, 然后再按单频点概率统计法把中心频点上的自噪声水平进行归纳, 进而可以获取跨数量级的统计结果差异, 得到单一频点与典型自噪声水平值的一一对应。
|
$
{f_k} = 0.00125 \times {\left({{2^{1/3}}} \right)^{k - 1}}
$
|
(4) |
fk为按三分之一倍频程划分的中心频率点;k为中心频率点的编号, k=1,⋯⋯,43。
|
$
{f_{k - h}} = 0.00125 \times {\left({{2^{1/3}}} \right)^{k - 1}} \times {2^{1/2}}
$
|
(5) |
|
$
{f_{k - l}} = 0.00125 \times {\left({{2^{1/3}}} \right)^{k - 1}} \times {2^{ - 1/2}}
$
|
(6) |
fk-h是以fk为中心频点, 按照一个倍频程进行平滑的频率上限;fk-h是下限
|
$
{N_{{f_{k - g}}}} = {\mathop{\rm Mean}\nolimits} \left({\sum\limits_{{f_{k - 1}}}^{{f_{k - h}}} {{N_{ig}}} } \right)
$
|
(7) |
Nfk-g是将第g个小时地震计自噪声计算结果中频率范围在fk-h和fk-1之间的自噪声计算结果Nig累加后求得的平均值, 并作为fk中心频点地震计自噪声水平的值, i的定义与式(3)中的i相同, Nig是第g个小时地震计自噪声计算结果中i号频点对应的值, g=1,……,1000,是1000hr计算结果的序号
|
$
P{r_{{f_{kj}}}} = \frac{{{A_{{f_{kj}}}}}}{{1000}} \times 100\%
$
|
(8) |
Afkj表示在中心频点fk, 自噪声水平为jdB的地震计自噪声计算结果出现的个数;Prfkj表示在中心频点fk、自噪声水平为jdB的地震计自噪声计算结果出现的概率;P、A、fk及j的定义与前面相同。
3 数据处理与分析
使用3套观测系统产出的连续1000hr垂直向观测数据按照三台法进行自噪声计算, 未剔除含有天然或非天然事件的记录。为了获取更多的低频段噪声水平的信息, 同时使用了100Hz和1Hz采样的数据, 并进行了去均值和去倾斜的预处理。在计算功率谱密度时选取的窗口函数为汉宁窗(hanning window), 窗口长度为1440s, 相邻数据段的重叠长度为1296s。
3.1 单小时结果众值法
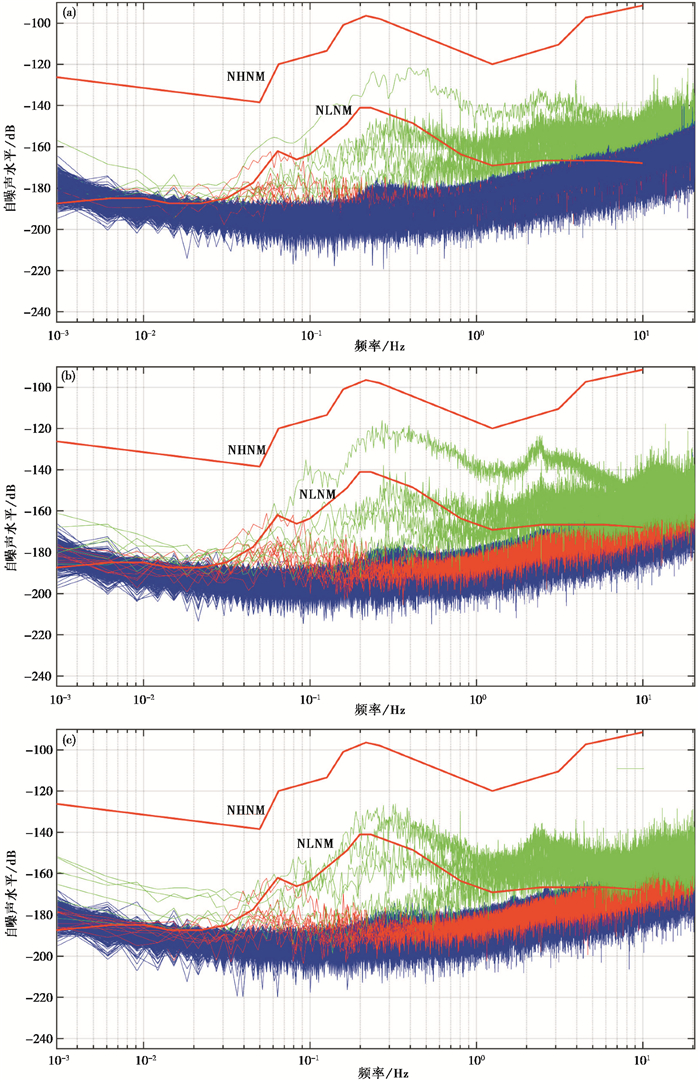
图 2(a)、2(b)、2(c)分别以单小时众值法的形式展示了1~3号地震计垂直向的自噪声水平结果, 从图 2可以看到3台地震计垂直向自噪声水平表现出来的共性与不同。
从共性上看, 3台地震计的自噪声水平形态大部分一致, 主要集中在一个弯曲的条带中, 整体表现为中间低, 两端缓慢抬升, 高频段相对较宽并在向低频段过渡的过程中逐步收窄, 在0.01~10.00Hz的频段低于NLNM模型(Peterson, 1993), 而在其他频率范围高出NLNM模型。值得注意的是, 该条带在0.2~0.4Hz处出现一个较小的集中隆起, 这样的结果可能是由地震计方位的微小不一致产生的(Gerner et al,2016), 也可能是仪器内部的生产工艺及使用时的安装水平导致的。
在3台地震计的自噪声计算结果中, 都有13条计算结果表现出明显的不同, 这13条计算结果所对应的观测记录时段相同, 按照原因分为以下2类, 并分别标为绿色及红色(图 2)。
绿色部分的4条结果整体形态上与地震台站背景噪声更为接近, 其中1条结果整体高于NLNM模型, 其余3条结果在0.03~2.00Hz低于NLNM模型。经核实这4条结果所对应时段的原始记录中都有1台地震计的观测记录丢数, 其中2018030401时段的6302缺数56min, 2018040316时段的6308缺数47min, 2018040612时段的6305缺数14min, 2018030115的6308缺数10min。
红色部分的9条结果整体形态上与地震计自噪声水平一致, 较为明显的差异表现在25~5s形成了明显凸起并高出其他结果10~40dB不等, 在这个隆起的频段, 3台地震计自噪声水平的形态和数值都比较一致。经核实, 这9条结果对应的原始记录中分别对应了远震及尾波。这些远震事件(UTC时间)包括:2018年2月25日18时28分中国台湾宜兰海域5.1级地震、2018年3月6日14时13分巴布亚新几内亚6.7级地震、2018年3月8日17时39分新爱尔兰地区6.8级地震、2018年3月26日9时51分新不列颠地区6.7级地震、2018年3月29日21时25分新不列颠地区6.9级地震及2018年4月8日16时34分日本本州西5.7级地震。
从差异性上看, 利用完整的无地震计事件的数据计算获取的3台地震计自噪声水平在部分频段的分布细节并不完全相同, 但数值上的差异不大, 如在低于0.02Hz的频段, 3号地震计自噪声结果分布相对分散, 2号地震计自噪声结果较之有所收敛, 而1号地震计自噪声则表现得较为紧致整齐, 在高于0.02Hz的频段, 1号及2号地震计自噪声形态基本一致, 而3号地震计自噪声结果显得相对分散, 且有部分频点结果峰值达到-220dB。3台地震计的自噪声水平结果受到观测记录缺数的影响程度不同, 这与自功率谱和互功率谱在三台法中的贡献率有关, 从图 2的结果中可以发现, 当某台地震计的观测记录缺数时, 其自功率谱的估算错误大小主导了自身自噪声形态的畸变程度, 而互功率谱估算错误所导致的影响则相对弱化, 我们发现在观测记录缺失的情况下, 功率谱的估算错误程度与缺数长度关系密切。
图 2的结果可以在一定程度上反映出3台地震计自噪声水平分布情况, 并且表现出受观测记录地震事件及缺数的影响。上千条结果以众值的形式集中画到一张图上, 既有重叠, 也有交叉, 使得这些结果只能提供连续运行的地震计自噪声水平的概况信息, 如固定频点上的噪声水平起伏区间、频域上的基本形态等, 而不能反映固定频点上不同噪声水平分布的疏密, 造成不同地震计的细节特征辨识困难。
3.2 单频点概率统计法
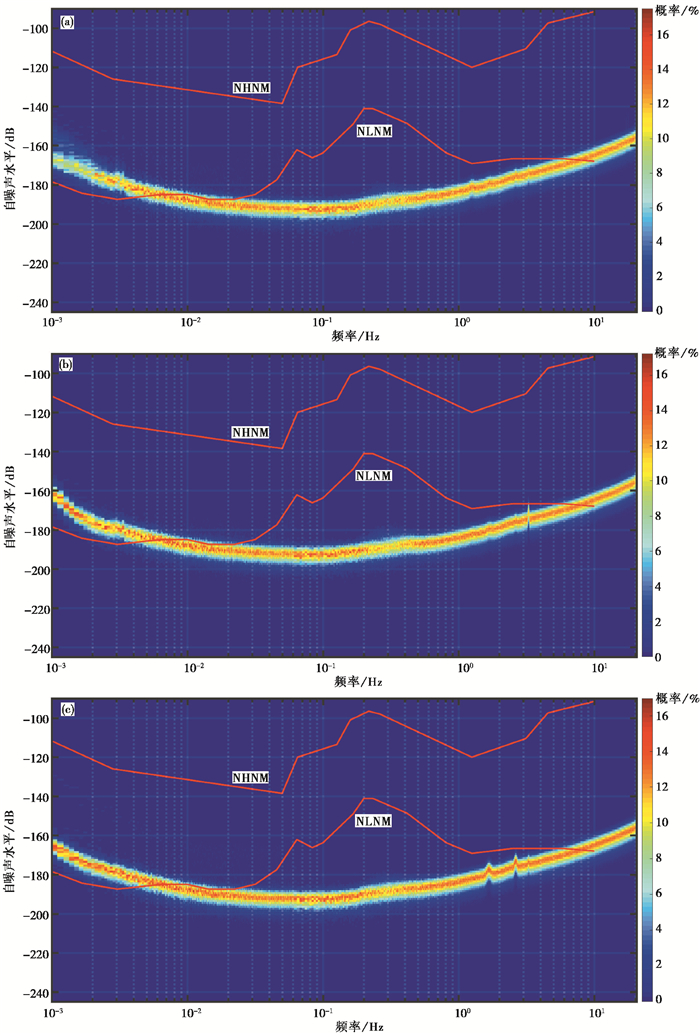
图 3(a)、3(b)、3(c)分别以单频点概率统计法的形式展示了1~3号地震计垂直向的自噪声水平结果, 图 3(a)、3(b)、3(c)为三维图的俯视图, 其中X轴为频率, Y轴为地震计噪声水平, Z轴为概率。Z轴的数值表示地震计自噪声水平的不同数值结果在对应频点上出现的概率大小, 并以不同色值显示。
由图 3可以看出, 3台地震计自噪声水平的整体分布形态基本一致, 高于10%概率的结果主要集中在一个5dB宽的凹形条带内, 形成了稳定的高概率区间, 在0.01~10.00Hz的频率区间内低于NLNM模型, 在其余频段高出NLNM模型, 在0.20~0.13Hz的二类海洋脉动频段都出现了一个轻微隆起。比较明显的区别出现在低于0.003Hz的频段, 1号地震计自噪声水平的结果明显不如2号及3号地震计集中。
从图 3的结果中已经能很清楚地了解测试地震计在不同频点上自噪声水平的概率分布情况, 并且可以得到一个结论, 即这3个测试地震计的自噪声水平在高于0.003Hz的频段, 整体一致较好, 高概率分布区间相对集中。但随之而来的问题是, 当高概率集中分布在一个宽为5dB的条带内时, 同一频点上不同自噪声水平的概率差异不大, 只有5%左右, 并没有超过1个量级, 在这样的前提下, 以最高概率(Sleeman et al,2012)对应的噪声水平来表征该频点的地震计自噪声水平模型的合理性仍然值得商榷。
3.3 分频带概率统计法
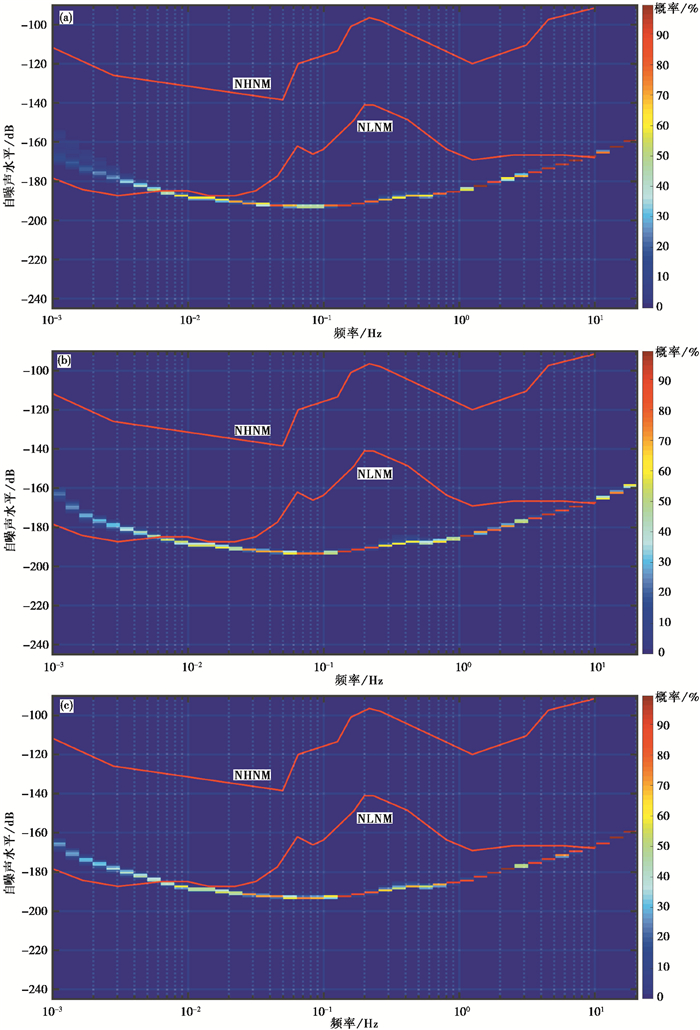
图 4(a)、4(b)、4(c)分别以分频带概率统计法的形式展示了1~3号地震计垂直向的自噪声水平结果, 图 4(a)、4(b)、4(c)同样是三维图的俯视图, 其中X轴为频率, Y轴为地震计噪声水平, Z轴为概率。Z轴的数值表示地震计自噪声水平的不同数值结果在对应中心频点上出现的概率大小, 并以不同色值显示。
由图 4可以看出, 3台地震计自噪声水平的整体分布形态基本一致, 在0.0067~10.0000Hz的频率区间内低于NLNM模型, 在其余频段高出NLNM模型, 在0.2~0.13Hz的二类海洋脉动频段都出现了一个轻微隆起, 高于10%的结果主要集中在一个2dB宽的凹形条带内, 最高概率达到了99%。比较明显的区别出现在低于0.003Hz的频段, 1号地震计自噪声水平的结果不如2号及3号地震计集中。
通过对每个小时的地震计自噪声水平结果进行平滑获得了对应于中心频点的地震计自噪声水平单一量值, 这使得每个子频带上的地震计自噪声水平特征信息可以集中反映到对应的中心频点上。当再对1000hr结果中各个中心频点上的自噪声水平值进行统计时, 就会使得长期在特征及量值上占据优势的自噪声水平以更为集中的高概率区间形式凸显出来。从结果上看, 这样的对比差异明显, 能够从得到的高概率区间中提炼出在概率上具有量级优势的典型值, 为地震计自噪声水平的数学建模提供参考。
4 结论
本文采用同址观测方式进行地震计自噪声水平测试实验, 使用三台法(Sleeman et al,2006)对连续1000hr记录进行计算, 利用概率统计对计算结果进行分析, 并以3种不同方式进行表现, 得到的结论如下:
在不使用概率统计方法的情况下, 从连续计算结果可以获取地震计自噪声水平的基本分布区间, 发现异常计算结果, 并可逐条追溯至原始数据分析原因。大量的计算结果以众值的形式罗列在一张图上, 造成无法获取地震计自噪声水平不均匀分布的区间特征, 不适合用作单个频点或子频带可靠的噪声水平描述。
使用概率统计方法对连续计算结果的单频点进行分析, 可以直接获取完整的地震计自噪声水平在固定频点上不均匀分布的概率区间特征, 并可表现出不同地震计在不同频点上的细微区别。在多数计算结果正常的前提下, 会造成异常结果被忽略, 不利于异常结果溯源。在相对高概率集中的区间内, 概率值差异变化较小, 不宜以最高概率对应的噪声水平表征该地震计在固定频点上的噪声水平。
按照三分之一倍频程划分频带, 以一个倍频程进行平滑的方法对单小时自噪声计算结果进行重新整理, 并使用概率统计方法对整理后的结果进行分析, 将相对较窄的子频带内地震计自噪声水平的特征信息以单一量值的形式集中反映到中心频点上, 通过上千小时的统计样本会使得不同中心频点上噪声水平分布的高概率区间进一步收窄, 显著表现出噪声水平的不均匀分布特征, 对应于中心频点上不同噪声水平的高低概率差异普遍超过1个数量级, 使用固定中心频点上最高概率对应的噪声水平来表示该频段上地震计的自噪声水平时, 具有一定的可信度, 且为固定型号地震计建立稳定自噪声数学模型提供了可能性。这样的方法在多数计算结果正常的前提下, 同样会造成异常结果被忽略, 不利于异常结果溯源。
以上3种分析表达方式, 虽然各有优缺点, 但对于地震计这样需要长期稳定运行的地震专业观测仪器来说, 相对于天然地震及记录缺数等小概率异常情况, 使用第2种及第3种表达方式在表征地震计自噪声水平的非均匀分布特点上更为直接, 尤其是第3种表达方式可以为地震计使用者建立地震计自噪声模型及合理评价产出数据的可用性提供较为直观的参考。
5 讨论
在地震计自噪声水平的建模研究中, Ringler等(2011)基于三台法同址观测, 通过对多次实验结果进行初步统计得到最小噪声水平, 并以此建立了11个型号地震计自噪声的低噪声频率函数模型。该研究还将该模型与地震计的理论模型及多次实验结果的中值放到一起比较分析, 为在较宽的频率域内认识和把握不同型号地震计的自噪声水平提供了很好的参考, 有2个细节需要注意:
(1) Ringler等(2011)用于分析的观测记录均为长10hr的安静时段数据, 这样的数据在时间尺度及普遍性上都具有一定的局限性。
(2) 其中9个型号地震计的自噪声模型来源于垂直分向的统计结果, 而KS-1及KS-2000的自噪声模型中则还含有水平分向的贡献, 没有对地震计垂直分向与水平分向的自噪声水平细节特征进行区分对比。
Sleeman等(2012)提出基于概率统计分析STS2甚宽频带地震计的方法, 并以最高概率所对应的自噪声水平来作为模型与其他研究结果进行比较, 其中以下3点值得注意:
(1) Sleeman等(2012)为了拓展低频分析范围, 使用了每段8192s的LH通道数据, 获得的结果中低频达到了0.2mHz(5000s), 数据长度与分析结果周期比约为1.6, 而万永革(2012)指出在傅里叶变换中这样的比值应该不小于2。尽管Sleeman等(2012)使用的单段数据长度与分析结果周期比不足2, 但采用的数据样本时间为1年, 在这样的情况下所获得结果在统计学上的意义值得进一步探索。
(2) 为了拓展低频分析区间, Sleeman等(2012)在计算分析过程中同时使用了40点采样的BH通道数据和1点采样的LH通道数据, 结果结合的频点为0.01Hz, 而为了同样的目的, Ringler等(2010a)在联合使用2种采样率数据时, 结果结合频点设定在0.0075Hz。在联合使用2种采样率数据时, 如何确定最佳的频率结合点还需要进一步的探讨。
(3) 当相对高的概率都集中在1个条带内, 且差异不超过1个量级时, 以最高概率对应的自噪声水平组合作为模型的合理性值得进一步讨论。
事实上, 地震计的真实自噪声受到空间环境变化、制造工艺(Ringler et al,2011)、安装方法(Sleeman et al,2006)及元器件老化等诸多因素影响, 其长期变化趋势也是需要进一步研究的内容。分析这些因素对地震计自噪声结果影响的物理机制, 制定相应的措施抵消或是降低这些因素的影响, 对提高地震计的观测能力, 提升产出观测数据质量, 拓展地震计的应用范围都有益处。
另外, 地震计的自噪声计算结果还受到观测记录选取(Hutt et al,2010;Ringler et al,2011;Sleeman et al,2012)、传递函数准确性(Holcomb et al,1990;Evans et al,2010)、功率谱参数配置(Li et al,2015;Gerner et al,2016)及计算方法应用(Hutt et al,2010)等多种因素制约。在表达形式上又分为众值(Evans et al,2010)、中值和最小值(Ringler et al,2011)、均值(Sleeman et al,2012)及概率统计(Sleeman et al,2012)等多种表现形式。正是由于这些影响因素的存在, 使得在数据及算法都相同的前提下依然会出现计算结果差异的情况。
为此, Evans等(2010)及Ringler(2011)对地震计自噪声计算方法及流程的标准化及统一化进行过一定的阐述, 主要集中在观测记录挑选、仪器参数及功率谱参数使用等方面。低自噪声及其长期稳定性是高质量地震计必备的特性, 而如何客观、准确地评价这2项指标, 则需要建立一套完整且规范化的测试标准作为支撑。童汪练①初步提出了一套地震计自噪声测试“建标评估”的测试及评价标准, 从测试时长、计算参数配置到数据分析处理进行了规范化的设计, 给出了可以量化打分的地震计自噪声评价指标, 对更全面合理地评价地震计自噪声水平有指导意义。本研究提出的分频带概率统计法正是基于概率统计和窄带信息相结合对长期运行地震计的自噪声水平的分析, 其形态的变化恰恰能在一定程度上反映地震计自噪声水平的长期稳定性, 有助于进一步完善地震计自噪声“建标评估”的评价体系。
①童汪练, 2017, 地震计自噪声测试《建标评估》初步探讨。
获取可靠的地震计自噪声数学数值模型, 对建立规范、科学且完善的地震计自噪声评测体系, 正确评价观测系统的观测能力, 助力低频振动建标都具有一定意义, 也值得我们进一步深入研究。
致谢:
感谢山东省地震局及马陵山国家比测基地为本项工作提供仪器及数据支持, 感谢万永革教授在数字信号处理方面的指导, 感谢审稿专家及编辑老师给出的宝贵建议。
 2019, Vol. 35
2019, Vol. 35