2. 中国科学院大学计算地球动力学重点实验室, 北京 100049;
3. 国家海洋环境预报中心, 北京 100081
2. Key Laboratory of Computational Geodynamics, Chinese Academy of Sciences, Beijing 100049, China;
3. National Marine Environmental Forecasting Center, Beijing 100081, China
测定中小地震的震源机制解是地震学应用和研究领域中一项重要的工作。由于中小地震(M < 5.0)发生频率较高,其震源机制为区域构造和构造应力场等研究提供重要信息。震源机制解反映了震源区附近的应力状态,对大地震前后发生的中小地震震源机制的研究,有助于认识大地震的发震构造特征,探索大地震的孕育过程,并为研究大地震的动态破裂模型及强余震触发模型提供重要的约束条件(王勤彩等,2009)。利用中小地震矩张量反演得到的地震矩、震源机制解、震源深度等参数可以解释断层在地震前后具体的运动情况,并为地震灾害评估、震后地震应急服务(郭祥云等,2014)。
中小地震震源机制解求解方法主要有P波初动法、振幅比法以及矩张量反演法(俞春泉等,2009;崔效锋等,2011)。对于中小地震来说,由于震级小、能量弱,通常难以利用远场波形反演地震矩张量解(赵翠萍等,2008;唐兰兰等,2012),在观测资料不足的情况下,近场波形反演结果也存在着较大的不确定性。而对于稀疏台网区域,只有少量台站记录到清晰资料,仅仅依靠P波初动很难得到可靠的震源机制解,其在很大程度上依赖于P波初动资料的数量及其分布状况(胡幸平等,2008)。因此,反演稀疏台网记录的中小地震的震源机制解,是一项非常具有挑战性的工作。
本文以2017年1月4日西藏区域台网记录的仲巴县M4.7地震为例,首先利用西藏区域台网近震波形资料,采用ISOLA(ISO lated asperities)方法对该地震进行震源机制反演,并探讨了结果的稳定性和可靠性,确定其最佳震源机制解;然后利用清晰的P波初动资料,采用CSPS(cyclic scanning of the polarity solution)初动扫描法,利用P波初动极性资料和少量台站近震波形约束,获取最佳震源机制结果,并与ISOLA近震全波形反演结果相比较,验证联合约束反演方法的可行性。本文的工作将有助于中小地震震源机制的研究,尤其是稀疏台网记录的网缘或网外地震,为深入了解稀疏台网地区的区域构造和构造应力场等研究工作提供有力的数据支撑。
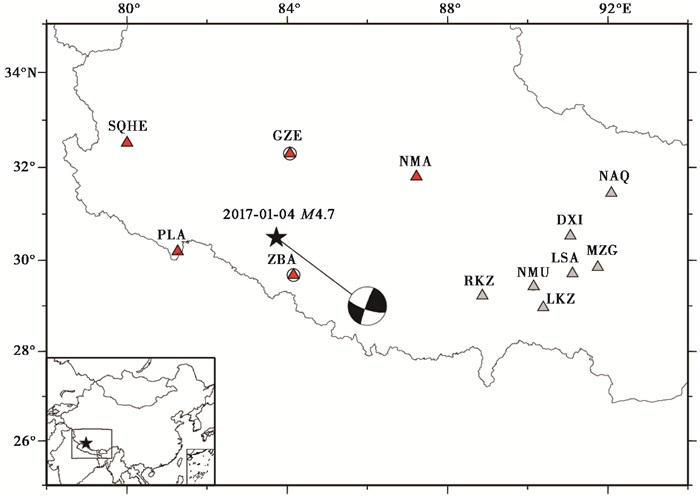
1 数据和方法 1.1 资料选取与处理本文使用了西藏自治区数字地震台网提供的台网观测报告给出的定位结果和区域地震波形资料,选取了12个清晰的地震台站的波形记录参与震源机制计算,图 1给出了本研究使用的台站分布,震中距为107~760km,在500km范围内仅有5个台站,其余台站主要集中分布在震中以东地区,台站分布稀疏且方位角覆盖较差。
|
图 1 西藏仲巴地震的震中位置和本研究使用的地震台站分布 五角星表示2017年1月4日西藏仲巴M4.7地震;红色三角形表示ISOLA近震全波形反演所用台站;灰色三角形和圆圈内红色三角形分别表示利用P波初动和近震波形联合约束反演所用台站;震源机制解为本文近震全波形反演结果 |
计算过程中,首先由波形观测资料读取P波初动极性,选取初动清晰的台站资料用于波形约束反演;然后将波形记录去除仪器响应、去倾斜以及去平均值等预处理,应用带通滤波器检查波形低频干扰成分(Zahradnik,2005;Zahradnik et al,2010),去除信号异常的台站记录,主要是因为低频干扰成分会对反演结果造成影响,降低反演结果的准确性。在实际反演过程中,为了突出有效信号,减小地壳精细结构对反演结果造成的影响,我们根据震中距范围选取合适的滤波频带。
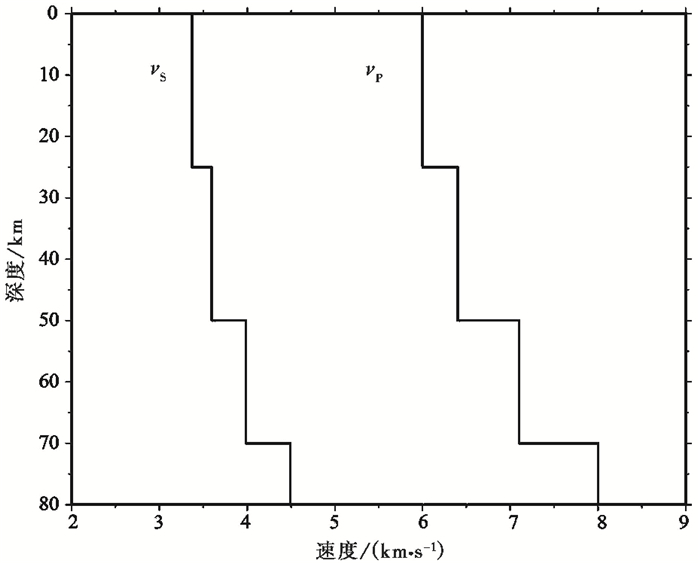
当采用ISOLA双力偶约束反演模式反演震源机制时,反演过程采用点源模型。选择震中距在500km范围内的5个台站的宽频带波形记录(最大震中距约为419km),对反演波形进行带通滤波,台站分布如图 1中红色三角形所示。为了减少地壳速度模型不确定性对研究结果的影响,滤波频带的下限频率应尽可能低,其主要受台站背景噪声影响,上限频率主要受震中距、地震大小和地壳速度模型的准确程度影响。一般来说,我们能够反演的波形记录的震中距不大于10倍MSW(MSW为最小剪切波长度)(Fojtíková et al,2014)。假设剪切波速度vs大约为3.5km/s,反演的最高频率为0.08Hz,其对应的MSW为12.5 s×3.5km/s=43.75km,所以,参加反演台站的最大震中距应小于10MSW(即437.5km)。本研究中通过对每个台站进行波谱分析,确定了每个台站的滤波频带范围为0.05~0.08Hz,采用二阶Butterworth滤波器进行滤波。我们采用图 2中的速度模型和离散波数法(Bouchon,1981)计算格林函数,采样间隔为0.2Hz。
|
图 2 地壳速度模型 |
当应用CSPS初动扫描法,利用P波初动资料和近震波形联合约束反演此次地震的震源机制时,我们选用了图 1中12个台站的P波初动极性资料,并联合距离震中最近的2个台站近震全波形台站资料(图 1中圆圈内的2个红色三角形)。在震源机制反演中,若选取的速度模型严重偏离真实地壳模型,其反演的结果具有较低的可信度,本文使用的一维速度模型参考了Crust2.0全球速度模型(Bassin et al,2000)。
1.2 研究方法本研究主要采用Sokos等(2008、2013)的ISOLA(ISO lated asperities)全波形矩张量反演方法,该方法采用单一点源或多点源模型,通过网格搜索和最小二乘法反演得到地震的最佳矩张量解。该方法具有纯双力偶(DC)、偏量矩张量(双力偶分量DC+补偿线性矢量偶极分量CLVD)和全矩张量(DC+CLVD+ISO分量)和固定震源机制4种求解方式,可以在点、线、面3种不同维度空间范围搜索最佳解,其中固定震源机制解求解方式仅反演得到矩心时间、深度和地震矩。同时可以根据台站分布选取单一或多重的地壳速度模型,降低震源-台站复杂射线路径(李飞等,2017)对反演结果的影响;反演过程中,该方法给出了多种量化参数来评估反演解的稳定性和可靠性,如VR、CN等参数。VR(Variance Reduction)为方差减少量,定义为
| $ {\rm{VR}} = 1 - \sum {{{(o - s)}^2}} /\sum {{o^2}} $ | (1) |
式中,o和s分别表示观测波形和理论波形;VR为表征观测波形和理论波形的拟合度的重要参数。CN(Condition Number)为条件数,其与参与计算的台站分布、滤波频段和速度模型有关,而与实际参与反演波形无关。反演过程中,需要对矩阵方程进行求解计算,即
| $ \mathit{\boldsymbol{u = G m}} $ | (2) |
式中,u表示观测波形矩阵;G为格林函数矩阵;m为模型参数矩阵。CN定义为矩阵 G的最大奇异值与最小奇异值之比,条件数越大,矩阵越病态(ill-conditioned),影响计算结果的稳定性。而在ISOLA反演过程中,未对 G进行矩阵分解计算,而是通过
为了反演稀疏台网记录的中小地震震源机制解,特别是在仅有少量近震台站波形记录,但较大震中距范围内台站记录P波明显可用的情况下,Fojtíková等(2014)等提出了CSPS方法,该方法利用P波初动极性资料和少量台站近震波形约束求解震源机制解的方法,其思路为:采用P波初动资料在空间范围内搜索震源机制结果,反演结果作为输入初始结果,联合近震波形数据,采用固定震源机制求解方式,计算波形拟合方差,选择波形拟合程度最高对应的震源机制结果为最优解。该方法最大的优势就是结合了P波初动极性解信息,约束了由于少量台站参与波形反演引起解的不稳定性情形。
为了验证P波初动和少量近震全波形约束反演中小地震震源机制解的有效性和可用性,我们采用ISOLA中的初动极性循环扫描法CSPS(Fojtíková et al,2014)对西藏仲巴M4.7地震求解震源机制解,采用ISOLA中纯双力偶约束的固定震源机制解求解方式,应用图 1中12个台站的P波初动极性资料,联合少量的近震全波形台站资料(图 1中圆圈内的红色三角形),计算波形拟合程度VR值,应用VR值量化固定震源机制反演结果。本文中应用FOCMEC(Snoke,2003)计算得到的多组走向角、倾角和滑动角值,作为CSPS初动扫描法的输入值。FOCMEC方法利用P波、SV波和SH波的初动方向以及振幅比联合测定震源机制解。通过比较理论计算和实际观测所得的P波、SV波、SH波的初动方向和振幅比矛盾数最小的方式得到震源机制解。在本研究中未采用S波初动和振幅比进行约束,仅采用P波初动极性资料计算初始震源机制解,通过近场全波形对输入初始解进行约束。
2 结果分析 2.1 近震全波形反演在反演过程中,首先参考西藏区域台网观测报告内容给出的初始地震定位参数(30.590°N,83.784°E;深度7km)。固定震中位置,在深度方向进行搜索,搜索范围为0~20km,搜索步长为2km;矩心时间搜索范围设为发震时刻前后4 s,搜索步长为0.1 s,反演不同深度的震源机制解,以波形最大拟合方差相应的震源深度为最佳矩心深度;其后,固定最佳矩心深度,以初始震中和最佳矩心深度为中心点,搜索范围为30km×30km,网格步长为5km×5km,共49个网格点,在平面网格内搜索最佳震源机制解。
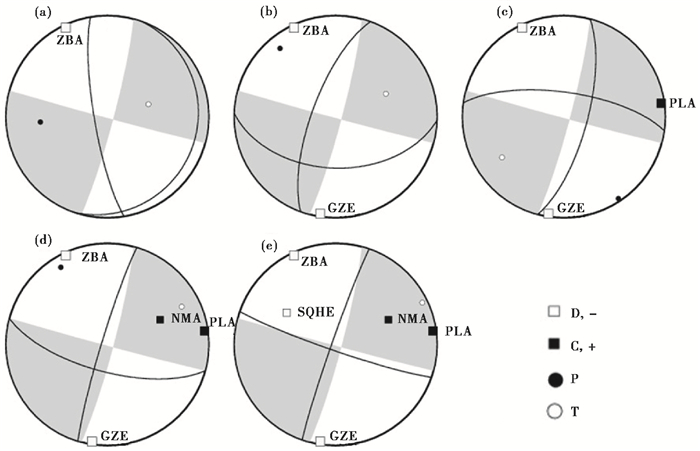
由于参加反演的台站数量、台站分布方位等因素影响计算震源机制结果的可靠性,为了得到最佳的反演结果,我们根据震中距范围由近及远分别采用不同的台站数量来反演此次地震的震源机制,反演得到矩心深度、矩心时间、断层节面解参数、矩震级MW以及相关解的质量评估参数等,详细信息如表 1所示。图 3为由不同台站反演得到的仲巴地震的震源机制,由图 3可以看出,台站数量少于2个的反演结果(图 3(a)、3(b)),与哈佛大学GCMT结果差别很大,震源机制解性质完全不同;台站数量大于2的反演结果(图 3(c)、3(d)、3(e))与哈佛大学结果相差不多。由此表明,少量台站波形记录反演的震源机制解结果可靠性低,并不能真实地反映地震的断层面解。
| 表 1 不同台站反演结果及质量评估参数 |
|
图 3 由不同台站反演得到的仲巴地震的震源机制 图(a)、(b)、(c)给出了不同台站数量(1~5个)时ISOLA反演震源机制结果和哈佛大学反演结果;黑色线为ISOLA反演结果对应的节线;黑色圆为P轴;白色圆为T轴;阴影区对应的节面为哈佛大学反演结果 |
由表 1可知,少量台站参与矩张量反演结果对应的台站观测波形和理论波形拟合程度非常好,方差VR>0.8,但条件数CN>6较大,反演矩阵的稳定性差,其对应的结果并不能表示真实的地震断层面参数。这也表明,基于波形的矩张量反演方法并不能仅仅通过波形拟合程度来评估反演结果的可靠性,要尽可能多的台站参与反演计算,并联合台站初动方向来检验反演结果的可靠性。
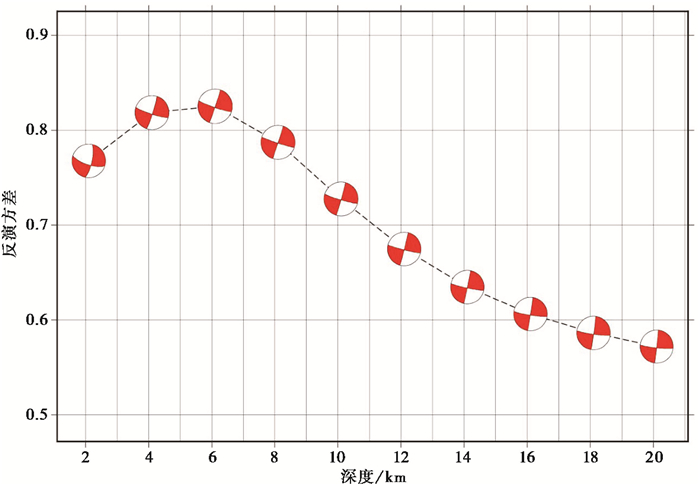
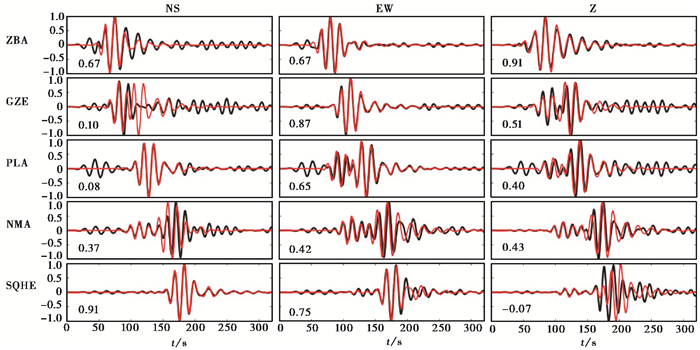
我们利用5个台站波形反演不同深度上的震源机制解,以波形拟合方差最大的震源深度和震源机制解作为最佳结果,图 4给出了不同震源深度下波形互相关之间的关系。从图 4可以看出,震源机制解在不同深度上变化不大,均显示为走滑型地震,震源深度6km处,波形互相关系数最大。我们得到此次地震最佳矩心深度为6km,与台网初始定位深度相差1km。图 5为固定震中位置垂直深度方向搜索西藏仲巴地震震源机制解对应的波形拟合图,可以看出方差减少量VR为0.71,其中,参与反演的5个台站波形的15个分量中,波形拟合方差减少量达0.5以上的有8个,占总分量的0.53%,可见台站波形拟合较好。
|
图 4 不同深度上仲巴地震的震源机制解及其反演方差 |
|
图 5 固定震中位置垂直深度方向搜索西藏仲巴地震震源机制解对应的三分量理论(红色)和实际(黑色)波形拟合图 波形下方数字表示波形拟合方差量;左侧大写字母表示台站名 |
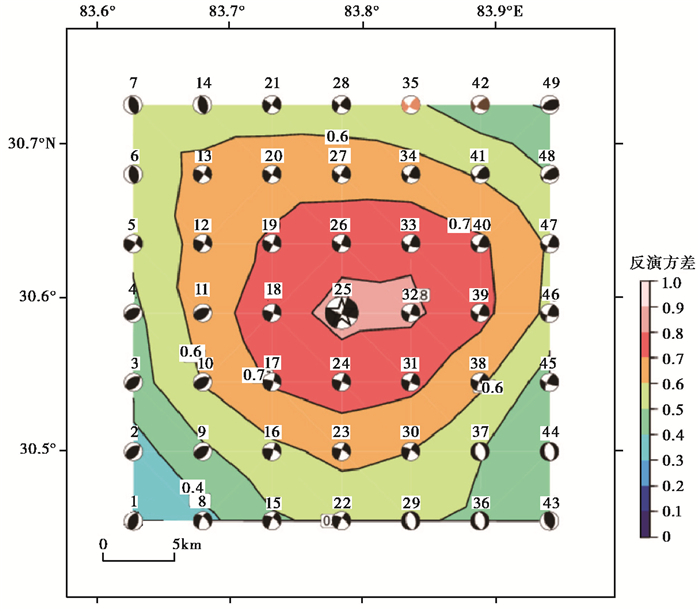
为了减少初始震中定位偏差对反演结果的影响,我们以初始震中和最佳矩心深度为中心点(25号网格点),在矩心深度平面网格区域内搜索空间最佳震源机制解,图 6显示了矩心深度平面上49个不同网格点上震源机制解及波形拟合相关系数值。由图 6可知,25号网格点对应的波形互相关系数最大,其对应的结果为最佳震源机制解,以最大震源球表示。矩心深度平面网格搜索的最佳双力偶机制解为,节面Ⅰ的走向/倾角/滑动角为109°/85°/-177°,节面Ⅱ的走向/倾角/滑动角为19°/88°/-4°,最佳矩心位置为30.590°N和83.784°E。在矩心深度平面网格区域内搜索最佳震源机制解对应的波形拟合图,方差减少量VR为0.71,与固定震中位置搜索结果一致,同时也表明,对于中小地震大多数初始破裂点与破裂的矩心位置是基本一致的(赵翠萍等,2008)。
|
图 6 不同网格点上震源机制解及波形拟合相关系数 五角星为震源机制搜索网格中心点在地表上的投影点;彩色条纹表示波形波形拟合相关系数;最大的震源球位置表示平面网格空间搜索的最佳震源机制解 |
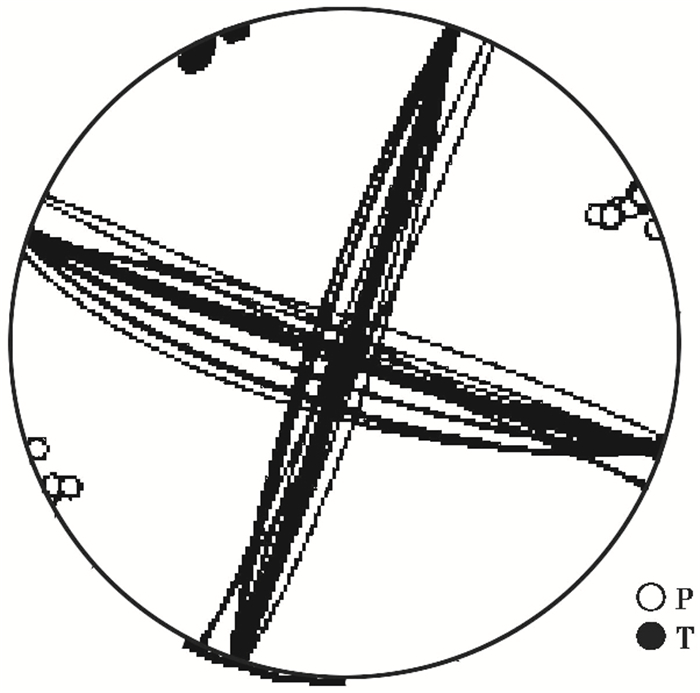
为了估算震源机制反演断层面解参数的不确定度,我们采用刀切法(Jackknifing method)对反演的参数进行不确定度分析(Sokos et al,2013;Boyd et al,2015)。考虑到不同方位和震中距地震记录对反演结果的影响,我们对参加反演的5个台站,每次减少1个台站共5次;每次减少1个分量共15次,合计进行20次反演,并把所有的反演结果投影在同一震源球上(图 7),由图 7可以看出,断层面节面线分布相对集中,说明多次反演结果比较稳定。
|
图 7 断层面参数不确定度的估计 黑色圆为P轴;白色圆为T轴 |
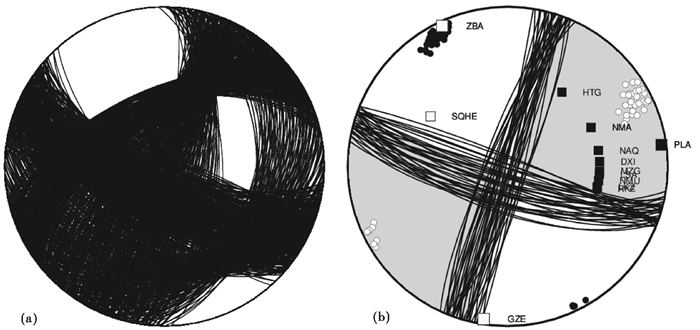
首先,我们采用FOCMEC方法,通过网格搜索,计算Crust2.0地壳速度结构模型下的震源机制解。反演过程中,设置的P波初动的矛盾数为0,得到500组可接受解(图 8(a))。由图 8所示,由于可用的P波初动资料少,且大部分台站分布集中,且初动向上,反演结果节面分布非常分散,很难判断哪组解为最佳解。
|
图 8 利用P波初动资料单独反演(a)和P波初动和波形约束反演(b)得到的仲巴地震的震源机制解 阴影区为ISOLA反演结果对应的压缩区;实心方形表示P波初动向上;空心方形表示P波初动向下;黑色圆为P轴;白色圆为T轴 |
为了得到最佳震源机制解,我们应用FOCMEC计算得到的多组走向角、倾角和滑动角值作为初动极性循环扫描法CSPS的输入值,采用ISOLA中纯双力偶约束的固定震源机制解求解方式,联合ZBA和GZE两个台站近震波形资料,计算观测波形与理论波形拟合程度VR值。通过选取0.9*VRopt~VRopt范围的解作为P波初动极性扫描计算得到的一组可行解,VRopt为最佳波形拟合震源机制解对应的方差减少量。本研究采用P波初动极性循环扫描法得到的最佳震源机制解为,节面Ⅰ的走向/倾角/滑动角为110°/67°/-172°,节面Ⅱ的走向/倾角/滑动角为17°/83°/-23°。
P波初动扫描计算的VRopt值为0.62,与全波形反演计算的VR值相比较小,波形拟合程度较低,但是通过P波初动循环扫描方法得到的可行解与ISOLA全波形反演结果相差不多,解的节面分布相对集中,P波初动方向与震源球体的压缩和膨胀特性相对应(图 8(b)),能够较好地反映小地震的震源特性。
总体来说,这2种方法给出的震源机制解具有很好的一致性。这在一定程度上验证了利用P波初动联合近震全波形求解震源机制解的可行性和可靠性。因此,我们认为应用极性扫描法方法约束反演震源机制解时,在台站数量较少时也能得到稳定可靠的结果,该方法对中小地震比较适用,有助于反演稀疏台网记录的中小地震震源机制解。
3 讨论与结论本研究利用ISOLA全波形反演方法,以西藏仲巴M4.7地震为例,计算稀疏台网记录的中小地震的最佳双力偶震源机制解,节面Ⅰ:走向109°/倾角85°/滑动角-177°,节面Ⅱ:走向19°/倾角88°/滑动角-4°,最佳矩心位置为30.590°N、83.784°E,最佳质心深度为6km,矩震级MW4.6。
西藏仲巴M4.7地震发生在喜马拉雅山西段,该区域地质构造较为复杂,发育着多条大型断裂(图 9)。从地质力学的角度来看,这个地方是构造应力易集中的地区,也是地震的易发区,震中区及周边发生的地震均为浅源地震,震源机制类型以正断层性质和走滑型性质地震为主。此次震中位于帕龙错-仓木错和嘉黎断裂交汇处。近年来,沿着这条断裂带曾发生过2004年7月6.7级地震、2005年4月6.5级地震(图 9)。震源机制结果表明,2017年1月4日西藏仲巴4.6级地震为走滑性质,这一结果与震源区域附近历史地震震源机制解具有相同性质。
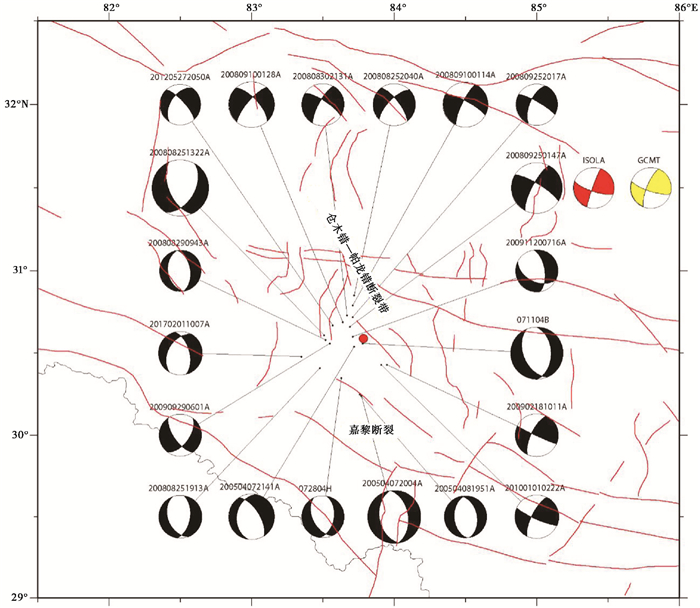
|
图 9 震源区附近历史地震震源机制解 黑色圆点代表研究区域历史地震(M≥5.0);圆形为本次仲巴地震初始震中位置;五角星形为矩心位置;红色沙滩球为本研究结果;黄色沙滩球为美国哈佛大学GCMT结果;黑线代表研究区内的主要断裂分布;历史震源机制来自于哈佛大学GCMT结果 |
为了比较近震全波形反演结果的稳定性和可靠性,我们进行多次反演,并对反演结果的不确定度进行定量分析,研究表明在少量台站记录波形参加计算的震源机制解存在较大的不确定性,反演过程中,不能单单依靠实际波形和理论波形拟合程度来判断结果的好坏,我们需要结合台站初动资料或更多台站参加反演来提高结果的准确性。
本文还采用P波初动和近震波形联合约束反演本次地震的震源机制,给出了最佳震源机制解,并与ISOLA近震全波形反演给出的结果具有较好的一致性。结果表明,当地震震级小,特别是台站较稀疏,初动资料少且方位角覆盖差,仅仅依赖P波初动资料很难确定震源机制解,在少量近台观测资料的情况下,联合少量台站的三分量波形记录进行约束反演,也能得到可靠的震源机制解。
ISOLA方法和现在较为广泛使用的CAP方法相同,均属于全波形反演方法,所不同的是反演时CAP方法是分别对体波和面波分别进行反演(张广伟等,2014;梁姗姗等,2017),而ISLOA方法是整个波形参与反演,并可将震源设置为单点源,也可以设置为多点源,且是在四维空间中搜索最优解。
综上,对于稀疏台网中小地震震源机制求解时,利用P波初动资料和近震波形联合约束反演方法是一种简洁明确的震源机制解量化方法,该方法可以稳定、可靠地计算中小地震的震源机制解。
致谢: 本研究使用了由希腊帕特雷大学提供的ISOLA近震全波形矩张量反演软件,大部分图件使用GMT软件包绘制,在此一并表示感谢。
崔效锋、胡幸平、俞春泉等, 2011, 汶川地震序列震源机制解研究, 北京大学学报(自然科学版):47(6), 47(6): 1063-1072. |
郭祥云、陈学忠、王生文等, 2014, 川滇地区中小地震震源机制解及构造应力场的研究, 地震工程学报, 36(3): 599-607. DOI:10.3969/j.issn.1000-0844.2014.03.0599 |
胡幸平、俞春泉、陶开等, 2008, 利用P波初动资料求解汶川地震及其强余震震源机制解, 地球物理学报, 51(6): 1711-1718. DOI:10.3321/j.issn:0001-5733.2008.06.011 |
李飞、张雪梅、陈宏峰等, 2017, 模拟退火方法在三维速度模型地震波走时反演中的应用, 中国地震, 33(3): 355-364. DOI:10.3969/j.issn.1001-4683.2017.03.001 |
梁姗姗、雷建设、徐志国等, 2017, 2016年1月21日青海门源MS6.4余震序列重定位和主震震源机制解, 地球物理学报, 60(6): 2091-2103. |
唐兰兰、赵翠萍、王海涛, 2012, 2008年新疆乌恰6.8级地震序列震源特征及帕米尔东北缘应力场研究, 地球物理学报, 55(4): 1228-1239. |
王勤彩、陈章立、郑斯华, 2009, 汶川大地震余震序列震源机制的空间分段特征, 科学通报, 54(16): 2348-2354. |
俞春泉、陶开、崔效锋等, 2009, 用格点尝试法求解P波初动震源机制解及解的质量评价, 地球物理学报, 52(5): 1402-1411. DOI:10.3969/j.issn.0001-5733.2009.05.030 |
张广伟、雷建设、梁姗姗等, 2014, 2014年8月3日云南鲁甸MS6.5地震序列重定位与震源机制研究, 地球物理学报, 57(9): 3018-3027. |
赵翠萍、陈章立、郑斯华等, 2008, 伽师震源区中等强度地震矩张量反演及其应力场特征, 地球物理学报, 51(3): 782-792. DOI:10.3321/j.issn:0001-5733.2008.03.019 |
Bassin C, Laske G, Masters G, 2000, The Current Limits of resolution for surface wave tomography in North America, Eos Trans AGU, 81: F897. |
Bouchon M, 1981, A simple method to calculate Green's functions for elastic layered media, Bull Seismol Soc Am, 71(4): 959-971. |
Boyd O S, Dreger D S, Lai V H, et al, 2015, A systematic analysis of seismic moment tensor at the geysers geothermal field, California, Bull Seismol Soc Am, 105(6): 2969-2986. DOI:10.1785/0120140285 |
Fojtíková L, Zahradnik J, 2014, A new strategy for weak events in sparse networks:the first-motion polarity solutions constrained by single-station waveform inversion, Seismol Res Lett, 85(6): 1265-1274. DOI:10.1785/0220140072 |
Snoke J A, 2003, FOCMEC:Focal mechanism determinations, Int Geophys, 81: 1629-1630. DOI:10.1016/S0074-6142(03)80291-7 |
Sokos E N, Zahradník J, 2013, Evaluating centroid-moment-tensor uncertainty in the New Version of ISOLA software, Seismol Res Lett, 84(4): 656-665. DOI:10.1785/0220130002 |
Sokos E N, Zahradnik J, 2008, ISOLA a Fortran code and a Matlab GUI to perform multiple-point source inversion of seismic data, Comput Geosci, 34(8): 967-977. DOI:10.1016/j.cageo.2007.07.005 |
Zahradnik J, 2005, Long-period pulses in broadband records of near earthquakes, Bull Seismol Soc Am, 95(5): 1928-1939. DOI:10.1785/0120040210 |
Zahradnik J, Plesinger A, 2010, Toward understanding subtle instrumentation effects associated with weak seismic events in the near field, Bull Seismol Soc Am, 100(1): 59-73. DOI:10.1785/0120090087 |
 2019, Vol. 35
2019, Vol. 35


