2. 上海市地震局, 上海 200062
2. Shanghai Earthquake Agency, Shanghai 200062, China
华北地区处于欧亚板块东缘,地质构造环境复杂,是我国大陆强震活动较频繁的地区之一。自GPS技术引入地震监测预测领域以来,华北地区一直是GPS重点观测区域(甘卫军等,2007),很多学者利用GPS资料对该区的水平运动与应变特征进行了研究(乔学军等,2008;刘峡等,2010;党学会等,2015;姚宜斌等,2015)。然而,华北地区形变信息较弱、干扰较强,计算地区应变场时,除收集采用高精度、高密度的输入数据外,应使用合理的计算模型,在避免引入系统误差的同时进行精度评定。
目前GPS应变场计算主要采用三角形法或插值法等方法,这类方法模型简明,但存在以下问题:①在数学上均存在一定的计算偏差;②对原始数据粗差抵抗性较差;③无法得到应变率计算精度以评价可靠性。
采用球面整体应变计算法计算应变率在数学上是无偏的(石耀霖等,2006;杨国华等,2010),但是,采用该方法需要位移或速度的数学解析式,而GPS站点分布不连续,其站点速率离散,采用多面函数法拟合GPS速度场可以获得区域运动速度解析式(刘经南等,2001),进而应用球面整体应变计算法。同时,由于得到了速度和应变率的数学解析式,可以根据误差传播率计算应变结果的误差,以评价结果的精度和可信度。
本文综合采用改进多面函数法和球面整体应变法构建无偏应变计算模型。利用华北中部地区CMONOC的GPS连续站数据,基于连续形变假设,采用改进多面函数法得到该区域GPS水平速率解析式,再用球面整体应变计算法计算华北中部地区地壳EW向线应变率、SN向线应变率、NE向剪应变率、面膨胀率,并初步评估其精度。
1 应变场计算模型及其精度评定 1.1 改进多面函数法拟合水平速度场采用多面函数拟合GPS水平速度场,可以由离散的GPS站点的位移或速率计算得到区域水平速度解析式,其数学模型为(Hardy,1978)
| $ {\mathit{\boldsymbol{S}}_{\left( {B,L} \right)}} = \sum\limits_{i = 1}^n {{\alpha _i}\theta \left( {B,L;{B_i},{L_i}} \right)} $ | (1) |
式中,B、L为纬度和经度;n为节点数;α为待定系数;θ(B,L;Bi,Li)为核函数。用矩阵的形式描述多面函数法,即
| $ \mathit{\boldsymbol{S}} = \theta \alpha $ | (2) |
根据正规方程可得
| $ \alpha = {\left( {{\theta ^{\rm{T}}}\theta } \right)^{ - 1}}{\theta ^{\rm{T}}}\mathit{\boldsymbol{S}} $ | (3) |
本文采用基于Tikhonov正则化的改进多面函数法(彭钊等,2019),该方法在经典最小二乘准则的基础上,引入正则化矩阵,删去核函数中的平滑系数,与原方法相比,其优点有:①规避了原方法平滑系数的不确定性;②去除了节点数不得大于已测点数的约束条件,采用更多的拟合节点,既可以有效提高拟合精度,又可以避免因站点分布不均造成的偏差,对于二维水平速度场拟合有重要价值。
引入Tikhonov正则化,原理是在偏差函数后增加一个正则化项,在正规方程里,通过在待定参数中引入正则化矩阵实现,即
| $ \alpha = {\left( {{\theta ^{\rm{T}}}\theta + {\mathit{\Gamma }^{\rm{T}}}\mathit{\Gamma }} \right)^{ - 1}}{\theta ^{\rm{T}}}\mathit{\boldsymbol{S}} $ | (4) |
取Γ=aIn,即单位矩阵的a倍,称为L2正则化。
此时式(4)变为
| $ \alpha = {\left( {{\theta ^{\rm{T}}}\theta + \lambda {I_n}} \right)^{ - 1}}{\theta ^{\rm{T}}}\mathit{\boldsymbol{S}} $ | (5) |
式中λ=a2为正则化系数,In为n阶单位矩阵。应用时,根据泛化误差最小化原则确定λ的取值。
1.2 球面整体应变计算法计算应变率球面整体应变计算法基于球面坐标而非直角坐标计算应变,在球面上计算应变,直接套用直角坐标系下的应变算式是有偏的。在已知平面运动解析式的情况下,基于球面坐标通过微分方程求解应变的计算式为(杨博等,2010;杨国华等,2010)
| $ \left\{ \begin{array}{l} {\varepsilon _{\rm{n}}} = \frac{1}{R}\frac{{\partial {V_{\rm{n}}}}}{{\partial {\boldsymbol{B}}}}\\ {\varepsilon _{\rm{e}}} = \frac{1}{{R\cos \mathit{\boldsymbol{B}}}}\frac{{\partial {V_{\rm{e}}}}}{{\partial L}} - \frac{{{V_{\rm{n}}}}}{R}\tan \mathit{\boldsymbol{B}}\\ {\varepsilon _{{\rm{ne}}}} = \frac{1}{2}\left( {\frac{1}{{R\cos \mathit{\boldsymbol{B}}}}\frac{{\partial {V_{\rm{n}}}}}{{\partial L}} + \frac{{{V_{\rm{e}}}}}{R}\tan \mathit{\boldsymbol{B}} + \frac{1}{R}\frac{{\partial {V_{\rm{e}}}}}{{\partial \mathit{\boldsymbol{B}}}}} \right)\\ {\varepsilon _\Delta } = {\varepsilon _{\rm{n}}} + {\varepsilon _{\rm{e}}} \end{array} \right. $ | (6) |
式中,εn、εe、εne、εΔ分别为NS向线应变率、EW向线应变率、NE向剪应变率、面膨胀率;Vn、Ve分别为N、E向速率;R为地球平均曲率半径。式(6)为应变计算的无偏算式,它适用于球面非均匀介质连续应变场的计算与分析。
采用改进多面函数法,可由离散点的N、E向的位移计算得到北、东向运动的解析式,进而计算研究区域内任一点N、E向速率Vn、Ve及其偏导。
1.3 精度评定根据式(1)、式(6),由离散GPS站点速率值计算得到区域应变率的数学解析式,进而可以根据误差传播率来计算应变率结果的误差。
由式(6)和误差传播律可求得各应变率分量方差为
| $ \left\{ \begin{array}{l} \sigma _{{\varepsilon _{\rm{n}}}}^2 = {\left( {\frac{1}{R}} \right)^2}\sigma _{\frac{{\partial {V_{\rm{n}}}}}{{\partial \mathit{\boldsymbol{B}}}}}^2\\ \sigma _{{\varepsilon _{\rm{e}}}}^2 = {\left( {\frac{1}{{R\cos \mathit{\boldsymbol{B}}}}} \right)^2}\sigma _{\frac{{\partial {V_{\rm{e}}}}}{{\partial L}}}^2 + {\left( {\frac{{\tan \mathit{\boldsymbol{B}}}}{R}} \right)^2}\sigma _{{V_{\rm{n}}}}^2\\ \sigma _{{\varepsilon _{\rm{e}}}}^2 = \frac{1}{4}\left[ {{{\left( {\frac{1}{{R\cos \mathit{\boldsymbol{B}}}}} \right)}^2}\sigma _{\frac{{\partial {V_{\rm{n}}}}}{{\partial L}}}^2 + {{\left( {\frac{{\tan \mathit{\boldsymbol{B}}}}{R}} \right)}^2}{\sigma ^2}{V_{\rm{e}}} + {{\left( {\frac{1}{R}} \right)}^2}\sigma _{\frac{{\partial {V_{\rm{e}}}}}{{\partial \mathit{\boldsymbol{B}}}}}^2} \right]\\ \sigma _{{\varepsilon _\Delta }}^2 = \sigma _{{\varepsilon _{\rm{n}}}}^2 + \sigma _{{\varepsilon _{\rm{e}}}}^2 \end{array} \right. $ | (7) |
根据式(2),各方向速率及其偏导数的方差为
| $ \left\{ \begin{array}{l} {\sigma _{{V_{\rm{n}}}}} = \theta {D_{{\alpha _{\rm{n}}}}}{\theta ^{\rm{T}}}\\ {\sigma _{{V_{\rm{e}}}}} = \theta {D_{{\alpha _{\rm{e}}}}}{\theta ^{\rm{T}}}\\ {\sigma _{\frac{{\partial {V_{\rm{n}}}}}{{\partial \mathit{\boldsymbol{B}}}}}} = \left( {\frac{{\partial \theta }}{{\partial \mathit{\boldsymbol{B}}}}} \right){D_{{\alpha _{\rm{n}}}}}{\left( {\frac{{\partial \theta }}{{\partial \mathit{\boldsymbol{B}}}}} \right)^{\rm{T}}}\\ {\sigma _{\frac{{\partial {V_{\rm{n}}}}}{{\partial \mathit{\boldsymbol{L}}}}}} = \left( {\frac{{\partial \theta }}{{\partial \mathit{\boldsymbol{L}}}}} \right){D_{{\alpha _{\rm{n}}}}}{\left( {\frac{{\partial \theta }}{{\partial \mathit{\boldsymbol{L}}}}} \right)^{\rm{T}}}\\ {\sigma _{\frac{{\partial {V_{\rm{e}}}}}{{\partial \mathit{\boldsymbol{B}}}}}} = \left( {\frac{{\partial \theta }}{{\partial \mathit{\boldsymbol{B}}}}} \right){D_{{\alpha _{\rm{e}}}}}{\left( {\frac{{\partial \theta }}{{\partial \mathit{\boldsymbol{B}}}}} \right)^{\rm{T}}}\\ {\sigma _{\frac{{\partial {V_{\rm{e}}}}}{{\partial \mathit{\boldsymbol{L}}}}}} = \left( {\frac{{\partial \theta }}{{\partial \mathit{\boldsymbol{L}}}}} \right){D_{{\alpha _{\rm{e}}}}}{\left( {\frac{{\partial \theta }}{{\partial \mathit{\boldsymbol{L}}}}} \right)^{\rm{T}}} \end{array} \right. $ | (8) |
参数α的单位权方差为
| $ \sigma _\alpha ^2 = \frac{{{V^{\rm{T}}}\mathit{\boldsymbol{P}}V}}{r} $ | (9) |
式中,V为残差;P为权矩阵;r为自由度。
其方差阵为
| $ \left\{ \begin{array}{l} {D_{{\alpha _{\rm{n}}}}} = {\left( {{\theta ^{\rm{T}}}\theta + \lambda {I_{\rm{n}}}} \right)^{ - 1}}\sigma _{{\alpha _{\rm{n}}}}^2\\ {D_{{\alpha _{\rm{e}}}}} = {\left( {{\theta ^{\rm{T}}}\theta + \lambda {I_{\rm{n}}}} \right)^{ - 1}}\sigma _{{\alpha _{\rm{e}}}}^2 \end{array} \right. $ | (10) |
采用华北中部地区93个CMONOC站(45连续站+48区域站)2011~2017年的连续时序数据计算各站点NS、EW两方向WGS84坐标系下的水平运动速率,根据稳定欧亚大陆的欧拉矢量将其换算到相对于稳定欧亚大陆的运动速率(图 1)。数据来自中国地震局GNSS数据产品服务平台(www.cgps.ac.cn)。
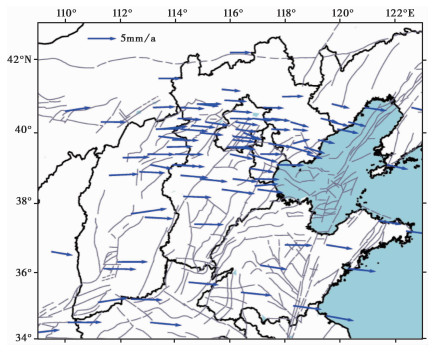
|
图 1 站点分布及其水平速率 |
采用改进多面函数法,根据式(2)、(5)得到区域内速率解析式;根据球面整体应变计算法代入式(6),计算0.1°×0.1°间隔点的EW向线应变率、SN向线应变率、NE向剪应变率和面膨胀率(刘经南等,2002);再利用式(7)~(10)计算各点应变率的精度,因所选取的站点都属于CMONOC站,观测条件和精度相仿,观测时间一致,故采用等权重方式进行计算。
2.2 改进多面函数法的拟合精度采用改进多面函数法,计算区域内速率解析式,核函数取基于大地长的正双曲型核函数(杨国华等,1990;黄立人等,1993),以全部93个站点作为节点。经过试算,NS向正则化系数取3.5,EW向正则化系数取0.9时,模型泛化误差最小,计算此时各站点的建模速率,其与实际速率的绝对值差值见表 1。
| 表 1 建模速率与实际速率的绝对差值(单位:mm/a) |
采用原多面函数法对站点速率进行拟合,取平滑系数为1,其余参数不变,其结果与改进多面函数的拟合结果的对比见表 2。
| 表 2 两种方法的拟合精度比较(单位:mm/a) |
由表 1、2可知,改进多面函数法各站点建模速率与实际速率相差不大,其平均残差为0.5mm/a左右,拟合精度相对于原方法有10%以上的提高,说明采用改进多面函数法建立的区域速度解析式符合整体速度场的趋势且精度高于原方法。计算1°×1°间隔点模型速率,区域模型推估速率分布如图 2所示。
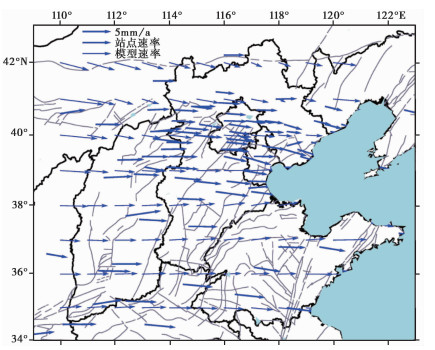
|
图 2 华北中部地区模型推估速率分布 |
计算得到的华北中部地区NS、EW向线应变率及其中误差如图 3、4所示。
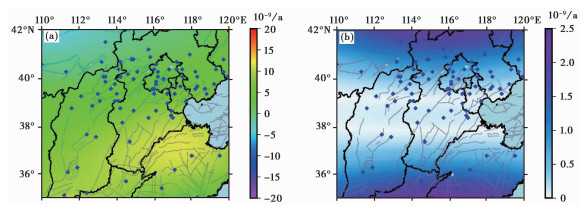
|
图 3 华北中部地区NS向线应变率(a)及其中误差(b) |
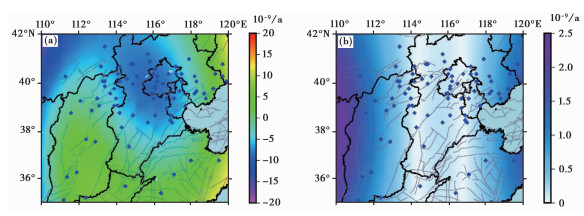
|
图 4 华北中部地区EW向线应变率(a)及其中误差(b) |
NS向线应变率的区间为-4.5×10-9~11.5×10-9/a,EW向线应变率为- 16.0×10-9~14.5×10-9/a,NS向线应变率的中误差为0.2×10-9~2.4×10-9/a,EW向线应变率的中误差的区间为0.2×10-9~2.5×10-9/a,计算结果精度较高。
在NS向,区域整体以张性为主,应变率相对较小,黄河下游带及向南延伸的区域呈相对张性高值,晋冀蒙交界及其以西地区呈较小的压性状态,区域内部呈近NW向的阶梯分布;在EW向,张渤带两侧及以西地区呈压性状态,山西带、黄河下游带及其以南地区呈张性状态,郯庐带山东段以东为张性相对高值地区,应变高值分布与大型断裂带分布基本一致,可能表明EW向线应变受构造运动控制较强。
2.4 华北中部地区NE向剪应变率和面膨胀率及其精度计算得到的华北中部地区NE向剪应变率及其中误差如图 5所示,面膨胀率及其中误差如图 6所示。
|
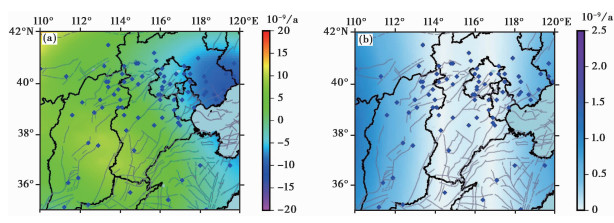
图 5 华北中部地区NE向剪应变率(a)及其中误差(b) |
|
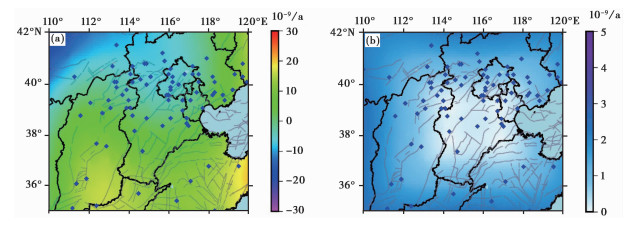
图 6 华北中部地区面膨胀率(a)及其中误差(b) |
NE向剪应变率区间为-10.5×10-9~14.0×10-9/a,中误差的区间为0.2×10-9~2.3×10-9/a,面膨胀率区间为-21.0×10-9~20.7×10-9/a,中误差的区间为0.3×10-9~2.5×10-9/a,计算结果精度较高。
区域内剪应变分布大体呈东负西正的特征,西部山西带中部和邢台地区,东部郯庐带山东段数值稍大,区域极值出现在唐山-秦皇岛地区,反映出该区域相对于首都圈其他地区较强烈的旋剪形变;面膨胀率分布整体表现为北压南张的格局,除晋冀蒙交界及其以西地区呈面收缩外,华北中部大部分地区呈面膨胀,山西带南部和郯庐带山东段数值较大。
2.5 应变率计算结果可靠性分析以应变率与应变率中误差的比值作为应变结果可靠性的评价指标,以2倍中误差作为应变计算结果真实可信的阈值,即
| $ E = \frac{\varepsilon }{{{\sigma _\varepsilon }}} \ge 2 $ | (11) |
式中,ε为应变率;σε为应变率中误差。
分别计算各格网点线应变率和剪应变率及其中误差的比值,其统计结果见表 3。
| 表 3 应变结果可靠性的统计 |
由表 3可知,NS、EW向线应变率和NE向剪应变率的计算结果评价为可信的比例都在85%以上,结合图 1~3,除了边缘地区误差稍高以外,大多数地区的应变率计算结果都真实可靠。
3 讨论与总结对弱形变地区的应变场采用无偏的计算方法是必要的,因为无偏模型能避免引入难以估计和消除的系统误差,而这样的系统误差对弱形变地区来说不可忽视,同时精度和可靠性评定也有助于评价计算结果的质量,并方便与其他研究者的结果进行对比。
本文综合采用改进多面函数法和球面整体应变法构建无偏应变计算模型,推导计算及精度评定公式,并给出可靠性的评价指标。基于华北中部93个CMONOC站2011~2017年的连续时序数据,计算华北中部地区线应变率及剪应变率,并计算相应的中误差及其比值,误差分析表明结果具有较高的精度和可靠性,证明采用基于改进多面函数和整体球面应变法的无偏应变计算模型计算弱应变应变率是可行的,且精度和可信度都较高,应变计算结果表明,华北中部地区应变率整体较小,高值区主要集中在大型断裂带及其附近区域,应变率梯度较高的区域主要有唐山地区、郯庐带山东段、山西带、张渤带等;区域整体以张性为主,晋冀蒙交界及其以西地区呈压性状态;唐山-秦皇岛地区具有区域内最高的剪应变率,表现出较强的旋剪形变。
本文采用的是同时间跨度CMONOC连续站和部分区域站的数据,计算使用等权方式,后续研究可通过补充更多区域站数据和多期流动GPS观测数据来提高应变场空间分辨率,反映更多细节信息,但是,不同区域站数据和流动观测数据的时间跨度和数据精度可能不同,需要采用不等权的方式进行计算。另外,本文仅就应变率场的分布特征进行了分析,在地质及地球物理构造解释方面存在不足,后续可通过结合地质、测震和其他地球物理信息对区域地壳构造变形及其动力学解释进行进一步研究。
党学会、郭炳辉、吕健, 2015, 基于GPS的华北地区地壳水平形变特征研究, 华北地震科学, 33(1): 1-4、24. DOI:10.3969/j.issn.1003-1375.2015.01.001 |
甘卫军、张锐、张勇等, 2007, 中国地壳运动观测网络的建设及应用, .国际地震动态, (7): 43-52. |
黄立人、陶本藻、赵承坤, 1993, 多面函数拟合在地壳垂直运动研究中的应用, 测绘学报, 22(1): 25-32. DOI:10.3321/j.issn:1001-1595.1993.01.004 |
刘经南、施闯、姚宜斌等, 2001, 多面函数拟合法及其在建立中国地壳平面运动速度场模型中的应用研究, 武汉大学学报(信息科学版), 26(6): 500-503、508. |
刘经南、姚宜斌、施闯, 2002, 中国地壳运动整体速度场模型的建立方法研究, 武汉大学学报(信息科学版), 27(4): 331-336. |
刘峡、马瑾、傅容珊等, 2010, 华北地区现今地壳运动动力学初步研究, 地球物理学报, 53(6): 1418-1427. |
彭钊、陈志遥、李赫, 2019, 一种基于Tikhonov正则化的改进多面函数拟合法, 大地测量与地球动力学, 39(3): 78-82. |
乔学军、陈颙、王琪等, 2008, 首都圈地区现今地壳运动的GPS观测与构造活动模拟, 武汉大学学报(信息科学版), 33(7): 692-696. |
石耀霖、朱守彪, 2006, 用GPS位移资料计算应变方法的讨论, 大地测量与地球动力学, 26(1): 1-8. |
杨博、张风霜、占伟等, 2010, 水平运动场滤波实验与应变计算, 大地测量与地球动力学, 30(5): 106-112. |
杨国华、黄立人, 1990, 速率面拟合法中多面函数几个特性的初步数值研究, 地壳形变与地震, 10(4): 70-82. |
杨国华、武艳强、杨博等, 2010, 应变计算与分析的若干问题及有关偏差的修正, 大地测量与地球动力学, 30(4): 59-63. |
姚宜斌、刘强、江国焰等, 2015, 华北地区应变率及其精度评定, 武汉大学学报(信息科学版), 40(10): 1317-1323. |
Hardy R L, 1978, The application of multiquadric equations and point mass anomaly models to crustal movement studies, NOAA Technical Report.
|
Wu Y Q, Jiang Z S, Yang G H, et al, 2011, Comparison of GPS strain rate computing methods and their reliability, Geophys J Int, 185(2): 703-717. DOI:10.1111/gji.2011.185.issue-2 |
 2019, Vol. 35
2019, Vol. 35


