昆明基准地震台地面与井下记录地震差异分析
李雷, 邓存华, 黄瑶, 钱文品, 谭文正
中国地震  2019, Vol. 35 2019, Vol. 35 Issue (1): 96-108 Issue (1): 96-108
|
云南地处高原地区,地震台站观测仪器直接放在山洞内基岩上,观测条件优于平原地区,但随着社会的发展尤其是城市的扩张和交通网的建设,地震台站的观测环境受到影响。深井观测与地面观测相比可以有效地降低人类活动造成的高频噪声干扰,深井观测能否解决云南地区面临的观测环境问题,是我们所关心的。我国井下地震观测始于20世纪70年代,观测台站主要分布于京、津、冀、沪等沉积层厚的平原地区,使用短周期地震仪,采用模拟记录进行观测。许多学者曾对地面和井下观测进行过对比研究,张寿康等(1986)对河北涿县井下摆(短周期768)与地面摆(短周期768)进行对比研究;周焕鹏(1986)对菏泽地震台深井摆(短周期768)与地面摆(DD-1)记录的地方震进行差异分析;蔡耐芳(1990)对天水地震台短周期井下摆与地面B73、64仪垂直向记录进行对比研究;张新东(2002)对邯郸台网的井下摆(短周期JD-2型)和地面摆震级和波形进行对比分析;仇中阳等(2006)对淮安地震台短周期井下摆记录震级与台网震级进行对比研究。“十五”以来我国地震观测进入数字化时代,井下地震观测也全面数字化,既有短周期又有宽频带观测。裴晓等(2013)对张江台地表与深井噪声进行对比分析;毛华锋等(2014)对江苏部分井下台与地面台震源参数进行对比研究;仇中阳等(2014)对苏北地面台与井下台地震波形进行频谱分析。研究表明对沉积层较厚的平原地区,短周期深井观测可以有效地降低背景噪声,提高观测系统的信噪比,获得更多微弱的地球物理信息。
笔者之前通过对背景噪声的分析,发现昆明基准地震台(以下简称“昆明台”)测震观测井在1~20Hz频带内降噪效果明显,0.010~0.033Hz频带内噪声不降反升(李雷等,2017),那么在记录地震方面情况又如何呢?本文将以昆明台为例,对地面和井下地震计所记录的地震进行信噪比、P波到时差、波形相关性和频谱分析,从而得出地面与井下记录地震的差异情况。
1 台站概况及资料的选取 1.1 台站概况昆明台地处昆明市北郊黑龙潭,位于滇东断裂系黑龙潭-官渡断裂带上,台基为二叠纪石灰岩。台站观测山洞位于台站办公楼后面山体内,山洞深47m,覆盖层厚度约40m,表 1中的地面台地震计就架设在山洞内。测震观测井位于台站院内,成井深度为202.5m,井底斜度为0.62°,地震计型号为GL-S60B井下宽频带地震计,校正方位角为5.75°,产出资料已经过方位角校正处理。
| 表 1 地面台与井下台的仪器情况 |
对2016年12月16日~2017年12月31日,地面摆BBVS-60(代码hlt)及井下摆GL-S60B(代码ksj)所记录的地震事件进行选取。
1.2.1 地震事件选取要求在速度波形上记录清晰,可识别P波、S波的地震事件,以减小背景噪声对分析结果的影响。本文共选取地震238个,其中近震124个,远震104个,极远震10个,来进行波形差异分析。近震的震级范围为1~7级,震中距范围0°~9°;远震的震级范围为4~8级,震中距范围9°~105°;极远震的震级范围为6~8级,震中距范围105°~180°。
1.2.2 数据长度本文采用地震全波形数据(包括地震体波和面波)进行波形差异分析,为保证地震波形完整,数据长度选取如下:相关分析时,取初至震相到时前10s作为数据起点,震中距大于2.5°时,取面波与初至波到时差的2.5倍作为数据长度;震中距小于2.5°时,取S波与初至波到时差的2.5倍加10s作为数据长度。频谱分析时,取初至震相到时作为数据起点,震中距大于2.5°时,取面波与初至波到时差的2.5倍作为数据长度;震中距小于2.5°时,取S波与初至波到时差的2.5倍作为数据长度。
2 地震波差异分析方法 2.1 互相关时延检测对2个不同的离散随机信号序列x(i)、y(i),互相关函数定义为
| $ \begin{array}{l} {R_{xy}}\left(m \right) = \frac{1}{n}\sum\limits_{i = 0}^{n - 1} {x\left(i \right){\rm{y}}(i + {\rm{m}})} \;\;\;\;\;{\rm{m}} \ge 0\\ {R_{xy}}\left(m \right) = \frac{1}{n}\sum\limits_{i = 0}^{n - 1} {y\left(i \right){\rm{x}}(i - {\rm{m}})} \;\;\;\;\;{\rm{m}} < 0 \end{array} $ | (1) |
式中,m为时延;n为信号长度。当互相关函数取得最大值时,对应的m就是2个信号的时延。对于某一确定的地震信号,同一台站2套地震仪记录到的2个波形x(i)、y(i),波形高度相似,只存在时间上的延迟,可以通过计算2个波形的互相关函数来得到时延m,这个时延就可认为是P波的到时差。
2.2 相关分析相关系数Rxy(《数学手册》编写组,1979)反映了2个变量x、y之间的线性关系的密切程度,定义为
| $ {R_{xy}} = \frac{{{l_{xy}}}}{{\sqrt {{l_{xx}}{l_{yy}}} }} $ | (2) |
式中,
|R|越接近1,线性相关越大。当|R| = 1,称为完全线性相关;当|R| = 0时,称全无线性相关。
相关分析可用于时域也可用于频域,在时域内,用相关系数可以定量地描述地震波形的相似性;在频域内,相关系数可以定量描述地震波频谱的相似性。
2.3 频谱分析地震波频谱分析是对地震波数据进行快速傅里叶变换,将时域信号变换到频域,得到地震波的频率成分分布。
快速傅里叶变换(FFT)是离散傅里叶变换的快速算法,由下列公式定义(万永革,2012)
| $ 正变换 \;\;X\left(k \right) = \sum\limits_{n = 0}^{N - 1} {x\left(n \right){{\rm{e}}^{ - j\frac{{2{\rm{ \mathsf{ π} }}}}{N}nk}}}, \;\;\;k = 0, 1, 2, 3, \ldots, n - 1 $ | (3) |
| $ 逆变换\;\; x\left(n \right) = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {X\left(k \right){{\rm{e}}^{j\frac{{2{\rm{ \mathsf{ π} }}}}{N}nk}}}, \;\;\;n = 0, 1, 2, 3, \ldots, n - 1 $ | (4) |
式中,x(n)为随机信号序列;X(k)为经过傅里叶变换后的频率域内信号序列,其模为振幅谱的绝对值,用频率作横坐标,振幅作纵坐标,就可得到振幅谱。
3 地震波差异分析 3.1 信噪比分析结果信噪比是一个无量纲值,用倍数或分贝表示。信噪比越大,说明信号越好,噪声越小。为了对比地面和井下记录地震事件的信噪比,本文取地震初至P波前30s的背景噪声振幅均方根s1与地震事件全波(数据长度为面波与初至波到时差的2.5倍)振幅均方根s2之比来估算信噪比,即振幅信噪比SNR = s2/s1,以分贝形式表示:SNR = 20lg(s2/s1)。
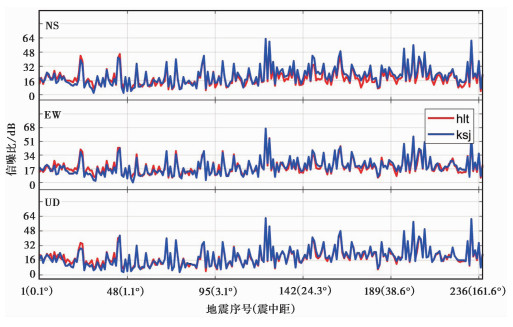
图 1为地面和井下记录地震事件三分向SNR对比图,238个地震事件按震中距由小到大排序。
|
图 1 地面和井下记录地震事件信噪比对比 |
为了便于分析,按震中距范围对地震事件信噪比进行偏差统计(表 2)。
| 表 2 地震事件信噪比偏差统计 |
当0° < Δ≤1°,井下台信噪比大多数比地面台信噪比低;当1° < Δ≤9°,井下台信噪比与地面台信噪比相比,NS、UD向多数地震略有提高;当9° < Δ < 180°,井下台信噪比与地面台相比均有提高,其中NS向提升最明显。
3.2 P波到时差异分析互相关时延计算P波到时差:对选取的地震,取地面台和井下台UD向记录波形,用式(1)计算波形的互相关函数,当互相关系数最大时,对应的时延就是两组地震波形的走时差,也就是P波到时差。
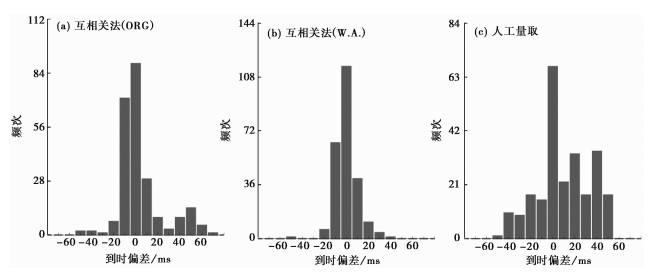
本文采用速度波形(ORG)和仿真W.A.波形分别计算互相关函数时延,到时偏差频次(图 2(a)、图 2(b))。可见,采用ORG波形互相关法计算的偏差范围为-50~70ms,主要偏差集中在-10~10ms,占总频次的78.1%;偏差-40~40ms的频次占总频次的90.9%;仿真W.A.波形计算的P波到时偏差范围为-50~40ms,主要偏差集中在-10~10ms,占总频次的90.5%;偏差-40~40ms间的频次占总频次的99.6%。
|
图 2 P波到时差频次分布 (a)速度波形结果;(b)仿真W.A.波形结果;(c)人工量取结果 |
为了与互相关法计算的P波到时差进行比较,人工量取238个地震事件P波到时,计算出P波到时差,绘出P波到时偏差频次分布图(图 2(c))。可见,人工量取偏差范围为-50~60ms,与互相关法基本一致,主要偏差集中在-40~50ms,偏差-10~10ms的频次占总频次的43%,偏差-40~40ms的频次占总频次的92.6%。
根据ORG互相关法、仿真W.A.互相关法和人工量取方法得到的结果,偏差最大仅70ms,可以认为地面台和井下台所记录地震的P波到时基本一致。
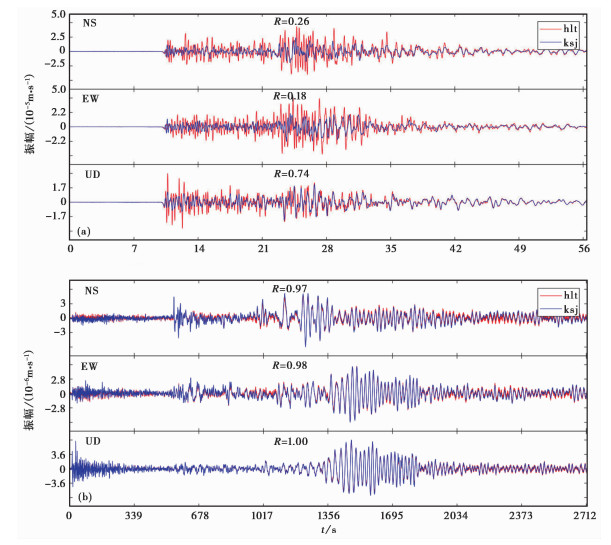
3.3 相关分析结果对选取的地震,按震中距排序,采用速度波形数据,根据式(2)计算地面台和井下台三分向波形的相关系数,地震波形相关性震例见图 3。图 3(a)为近震,NS和EW向地面和井下记录地震波差异较大,波形相似度很低,UD向相关性较NS、EW向好;图 3(b)为远震,NS和EW向波形相似度很高,UD向完全相关。
|
图 3 地震波相关性 (a)2017年5月1日云南峨山M4.0地震(Δ=1.0°);(b)2017年1月20日所罗门群岛M6.5地震(Δ=67.5°) |
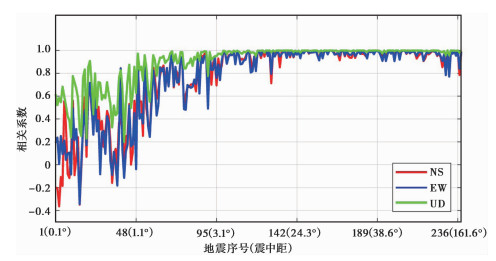
图 4为地面和井下记录地震三分向相关系数折线图,地震序号按震中距由小到大排序。由图 4可见,UD向的相关系数比NS、EW向大:UD向相关系数介于0.2~1.0,NS向相关系数介于-0.35~1.00,EW向相关系数介于-0.33~1.00。
|
图 4 时域波形相关系数 |
表 3为所选地震在不同震中距区间相关系数分布情况。由表 3可以看到,0° < Δ≤3.1°时,相关系数变化较大,几乎每个相关系数区间都有分布。
| 表 3 时域波形相关系数分布 |
3.1° < Δ < 180°时,波形相关度较高,NS向相关系数均大于0.7,完全相关的占23.8%,大于0.9以上占93%;EW向相关系数均大于0.7,完全相关的占18.2%,大于0.9以上占90.9%;UD向相关系数均大于0.9,完全相关的占65.7%,大于0.9以上占100%。
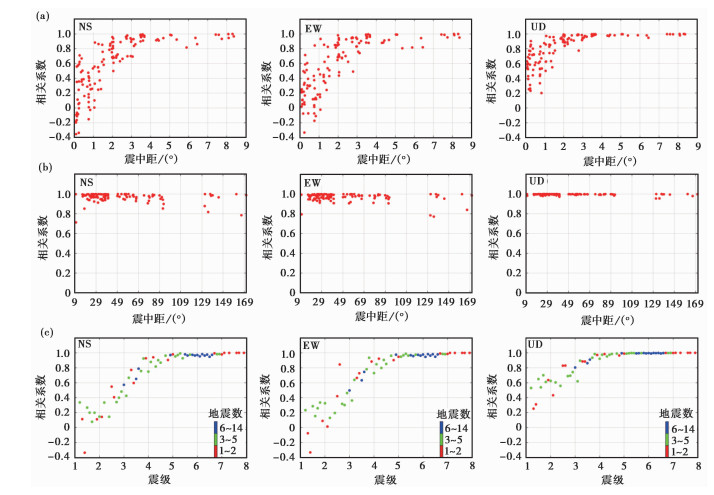
图 5为地震波形相关系数与震级、震中距的关系图。由图 5 (a)、5(b)可以看到,震中距小于1°时,相关系数很小,NS、EW向有负相关震例,随着震中距的增大,相关系数逐渐增大,震中距大于3.1°后,相关系数大多数大于0.9,少数介于0.7~0.9。
|
图 5 时域波形相关系数与震中距、震级的关系 (a)近震相关系数与震中距关系;(b)远震相关系数与震中距关系°;(c)相关系数与震级关系 |
图 5 (c)为相关系数与震级关系图,由图 5 (c)可以看到,当震级介于1~2级,地面台与井下台记录波形的相关系数较小,NS、EW向介于-0.4~0.4,UD向介于0.2~0.8,随着震级增大,相关系数线性增大,震级大于5级后相关系数趋于1.0。
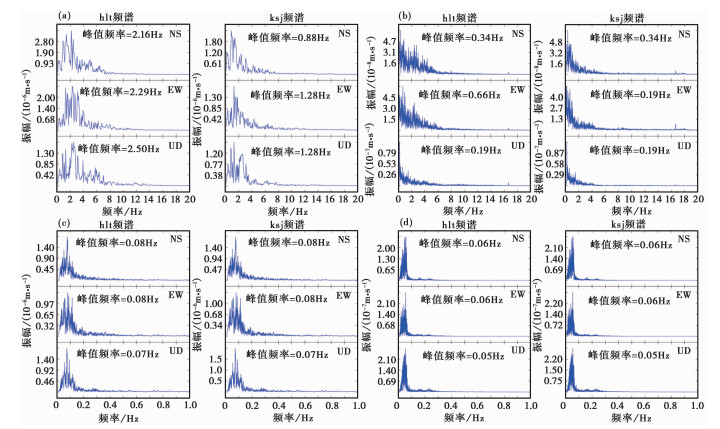
3.4 频谱分析结果对选取的地震,按震中距排序,采用速度波形数据,根据式(3)进行快速傅里叶变换,得到地面台和井下台三分向波形的频谱(图 6),图 6(a)~6(d)分别为地方震、近震、远震、极远震频谱,求出频谱的峰值频率。计算频谱时,近震频率范围取0.04~20.00Hz,远震、极远震的频率范围取0.008~10.000Hz。
|
图 6 地震波频谱 (a)2017年12月9日嵩明ML2.9地震(Δ=0.4°);(b)2017年3月30日云南鲁甸江ML4.1地震(Δ=1.9°);(c)2017年8月9日新疆M6.3地震(Δ=25.5°);(d)2016年4月25日智利M6.9地震(Δ=170.1°) |
通过对地震频谱图分析可以得出,近震的优势频率范围为0.06~8—15Hz,地面台和井下台的频谱差别较大;远震的优势频率范围为0.01~0.1—0.8Hz,地面台和井下台的频谱基本一致;极远震的优势频率范围为0.008~0.090Hz,地面台和井下台的频谱基本一致。
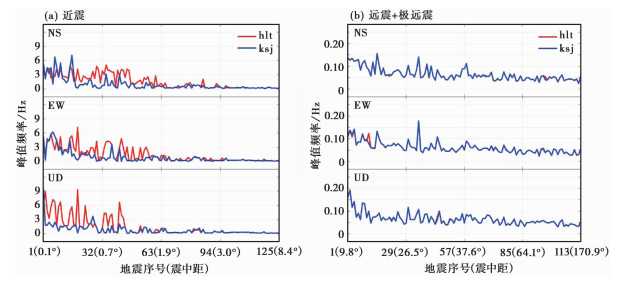
图 7为所选地震频谱峰值频率对比图,图 7(a)为近震峰值频率,图 7(b)为远震和极远震的峰值频率。由图 7可以看到,近震的峰值频率范围为0.10~9.57Hz,地面台和井下台的频谱峰值频率差别较大,震中距小于2°时,地面台的峰值频率明显高于井下台,震中距大于3.1°后,地面台与井下台的峰值频率基本一致;远震的峰值频率范围为0.03~0.19Hz,除个别震例外,两台的峰值频率基本一致;极远震的峰值频率范围为0.02~0.06Hz,两台的峰值频率完全一致。
|
图 7 频谱峰值频率对比 |
为了对地面台和井下台所记录地震的频谱差异有定量认识,本文对地震波振幅谱进行相关分析,用相关系数来表征二者的差异程度。
对选取的地震,按震中距排序,采用速度波形数据,根据式(3)进行快速傅里叶变换,得到地面台和井下台记录地震事件三分向波形的频谱,根据式(2)计算频谱相关系数。图 8为地面台和井下台记录地震的频谱相关性震例,其中,图 8(a)~8(e)为近震,震中距由小到大,图 8(f)为极远震。

|
图 8 地震波频谱相关性 (a)2017年12月9日嵩明ML2.9地震(Δ=0.4°);(b)2017年4月25日云南墨江ML3.7地震(Δ=2.1°);(c) 2017年8月15日广西靖西M4.4地震(Δ=3.7°);(d)2017年11月23日重庆武隆M5.1地震(Δ=6.3°);(e)2017年8月9日九寨沟M4.8地震(Δ=7.8°);(f)2017年5月11日南桑威奇M6.5地震(Δ=130°) |
通过对频谱相关性图分析可以得出:地面台水平向(EW、NS)在1.5~8.0Hz、UD在2~8Hz频段内频谱成分较井下台高,笔者认为属于地面台固有背景噪声,而地方震和近震优势频率恰好在这一频段内,导致地面台和井下台记录的地方震和近震频谱差别较大。随着震中距、震级的增大,对地震波频谱影响变小。远震和极远震优势频率分布小于1Hz,在频谱分析时未受影响。将远震和极远震频谱范围设置成0.008~20.000Hz,也可看到频谱差别(图 8(e)、8 (f))。
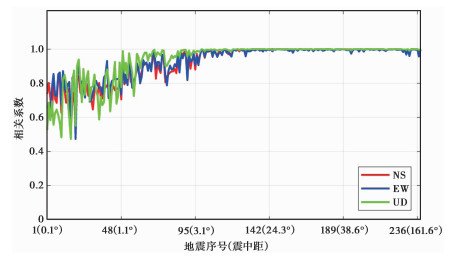
图 9为地面和井下记录地震三分向频谱相关系数折线图,地震序号按震中距由小到大进行排序。由图 9可以看到,震中距较小时频谱相关系数变化较大,NS频谱相关系数范围为0.52~1.00,EW、UD频谱相关系数范围均为0.47~1.00。震中距大于2°后,UD频谱相关系数大于NS、EW向。随着震中距增大,频谱相关系数逐渐增大。
|
图 9 频谱相关系数 |
表 4为所选地震在不同震中距区间频谱相关系数分布情况。由表 4可以看到,0° < Δ≤3.1°时,频谱相关系数变化较大,分布范围为0.47~1,且无完全相关震例。
| 表 4 频谱相关系数分布 |
3.1° < Δ < 180°时,频谱相关度较高,三分向相关系数全部大于0.9,频谱完全相关的NS向占81.1%,EW向占60.8%,UD向占90.2%。
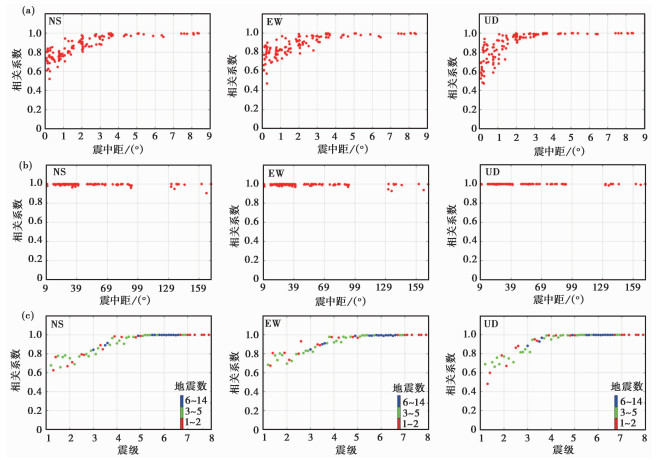
图 10为地面和井下记录地震频谱相关系数与震中距、震级关系图,图 10(a)为近震频谱相关系数与震中距关系图,由图 10(a)可以看到,随着震中距的增大,频谱相关系数逐渐增大,震中距大于2.1°后,频谱相关系数大于0.8,震中距大于3.1°后,频谱相关系数大于0.9。图 10(b)为远震和极远震频谱相关系数与震中距关系图,由图 10(b)可以看到,频谱相关系数全部大于0.9。图 10(c)为频谱相关系数与震级关系图,由图 10(c)可以看到,随着震级增大,频谱相关系数线性增大,震级大于5级后趋于1。
|
图 10 频谱相关系数与震中距、震级关系 (a)近震频谱相关系数与震中距关系;(b)远震频谱相关系数与震中距关系;(c)频谱相关系数与震级关系 |
通过对地面台和井下台在2016年12月16日~2017年12月31日所记录的238个地震进行信噪比、P波到时差、波形相关性和波形频谱分析,得到以下结论:
(1) 井下台信噪比与地面台信噪比相比提高有限。两台的信噪比高低与震中距有关,0° < Δ≤1°时,地面台信噪比比井下台信噪比高的占75%(NS)、77.3%(EW)、79.5%(UD);1° < Δ≤9°时,井下台NS向信噪比比地面台高的占59%,EW、UD向相差不大;9° < Δ < 180°时,井下台NS向信噪比提升明显,高于地面台的占97.3%,EW向高于地面台的占71.7%,UD向高于地面台的占63.7%。
(2) 用互相关时延法计算两台P波到时差,ORG波形和仿真W.A.波形计算结果一致性较好,但仿真W.A.的结果更优,P波到时偏差范围为-50~40ms,主要偏差集中在-10~10ms间,占总频次的90.5%;偏差为-40~40ms的频次占总频次的99.6%;偏差为-50ms的频次为1次,可以认为地面台和井下台记录地震的P波到时基本一致。
(3) 时域地震波相关系数UD向比NS、EW向大;相关系数分布于-0.35~1.00;相关系数与震中距、震级有关,震中距小于1°时,相关系数较小,NS、EW向有负相关的震例,随着震中距的增大,相关系数逐渐增大,震中距大于3.1°后,相关系数大于0.7,其中相关系数大于0.9以上的NS向占93%、EW向占90.9%、UD向占100%;随着震级增大,相关系数线性增大,当震级大于5级后趋于1。
将时域地震波转换到频域,进行频谱分析得出:频谱峰值频率与震中距有关,震中距小于2°时,地面台的峰值频率总体高于井下台,震中距大于3.1°后,两台的峰值频率基本一致;频谱相关系数分布范围为0.47~1.00;频谱相关系数与震中距、震级有关,随着震中距的增大,频谱相关系数逐渐增大,震中距大于3.1°后,频谱相关系数大于0.9;随着震级增大,频谱相关系数线性增大,当震级大于5级后趋于1。
综合时域相关分析和频谱分析结果得出,震中距小于3.1°时,地面台和井下台所记录地震波形差异较大,波形相关度很低甚至不相关;震中距大于3.1°后,两台记录地震波相关度很高。
(4) 地面台和井下台1.5~8.0Hz背景噪声差异,是震中距小于3.1°时地震波形差异的主要原因。在频域分析中,地方震和近震优势频率恰好在这一频段内,二台的频谱差别较大,随着震中距增大,地震波的优势频率逐渐离开此频段,对频谱的影响逐渐减小,随着震级增大,频谱差异减小;远震和极远震优势频率分布小于1Hz,未受此影响。而时域分析中,1.5~8.0Hz的成分差别一直都在,对震级大、信噪比高的地震影响小或无影响,对震级小、信噪比低的地震影响大。
(5) 李雷等(2017)得出在1~20Hz频段内,井下台噪声明显减小,2~8Hz降噪明显,最高达10dB;0.01~0.033Hz频段内,噪声不降反升。高频噪声结论与本文结论(4)基本一致,说明井下地震观测在降低地面高频噪声干扰的同时,对优势频率以高频为主的地方震及近震的地震波形有衰减。在本文分析中,虽是选取信噪比较高的地震,但近震波形较短且震级相对较小,可以看到高频噪声的影响;远震和极远震震级较大,低频噪声基本无影响。同时,在时域、频域相关分析时数据起点的选择和全波数据长度的取值等都可以减少背景噪声对分析结果的影响。
蔡耐芳, 1990, 兰州电传台网天水台井下摆记录特征, 地震地磁观测与研究, 11(5): 51-55. |
李雷、钱文品、邓存华等, 2017, 昆明地震台地面与井下地震观测背景噪声对比, 地震地磁观测与研究, 38(5): 86-95. DOI:10.3969/j.issn.1003-3246.2017.05.016 |
毛华锋、张义德、仇中阳等, 2014, 江苏部分测震台井下与地面观测震源参数对比, 四川地震, (3): 43-47. |
裴晓、尹继尧、杨庭春, 2013, 张江台地表与深井地震观测对比分析, 地震工程学报, 35(2): 366-371. DOI:10.3969/j.issn.1000-0844.2013.02.0366 |
仇中阳、郑照福、周政等, 2006, 淮安地震台井下测震的偏差研究及校正, 地震地磁观测与研究, 27(增刊): 40-50. |
仇中阳、毛华峰、陈健等, 2014, 苏北测震台网地面和井下地震记录波形频谱分析, 地震地磁观测与研究, 35(3/4): 105-111. |
《数学手册》编写组, 1979, 数学手册, 837~838, 北京: 高等教育出版社.
|
万永革, 2012, 数字信号处理的MATLAB实现, 2版, 343~345, 北京: 科学出版社.
|
张寿康、张碧晖、左素军, 1986, 井下与地面地震观测对比研究, 华北地震科学, 4(4): 79-84. |
张新东, 2002, 邯郸台网深井摆与地面摆记录分析对比, 地震地磁观测与研究, 23(1): 65-69. DOI:10.3969/j.issn.1003-3246.2002.01.011 |
周焕鹏, 1986, 深井摆与地面摆的记录差异, 地震地磁观测与研究, 7(6): 65-72. |