0 引言

地下水是分布于地壳深部岩体中最活跃的组分之一，对地震具有敏感的响应，这已经得到了很多前人的证明(Wang et al，2004)，因此井水位的同震响应也是学者用来监测地震的手段之一。井水位对固体潮的响应也较明显，引潮力(太阳、月亮及其它星球作用于地球的合力)使固体地球发生周期性的压缩与膨胀，含水层的孔压也会产生增大与减小，井与含水层之间产生压力差，进而发生水流交换，井水位发生周期性波动。通过研究井水位对固体潮的响应，计算井水位潮汐参数(潮汐因子和相位差)，分析潮汐参数变化特征，可了解到含水层介质及一些水力参数变化特征，特别是水流运动特性及其随时间演化的特性(Bredehoeft，1967)。

地震不仅可以影响近场应力，同时也可以以地震波形式产生动应变，不论是从引起孔压变化还是从沉积物固结与液化方面解释，地震都可以改变含水层的渗透系数。前人对地震可以改变含水层渗透系数进行过研究(Elkhoury et al，2006；Wang et al，2009)，然而，对于已知井-含水层本来的水流运动方向、地震发生前后井-含水层水流运动方向会发生哪些改变，及其改变原因的研究甚少。本文基于前人研究，在系统研究井水位同震响应的基础上，开展不同类型的地震前后井水位潮汐参数变化关系研究，分析变化特征并探讨其影响机理。

云南弥勒井井水位对地震具有敏感的响应，地震前后水位波动较大，潮汐响应也较明显，很多学者对云南弥勒井做过研究，车用太等(2015)在气汞(Hg)观测中记录到了2015年的尼泊尔8.1级地震的同震效应。石云等(2013)对于地下水异常分析的研究表明弥勒井是一口混合流井，且地震可以改变其含水层的导水性，从而引起井水位潮汐振幅和相位差的变化。Shi等(2014)通过对潮汐参数变化特征分析推导含水层水力参数的变化，研究表明含水层水力参数变化是引起弥勒井地下水位与温度呈正相关性的主要原因。唐彦东(2015)的研究表明弥勒井井水位的同震效应较明显，且有些地震震后水位会逐渐恢复，在地震波的作用下，震后含水层的水力参数发生改变，渗透系数增大。前人的研究结果表明云南弥勒井井水位同震响应较好，潮汐响应较显著。因此本文选取弥勒井来研究地震引起的水流变化特征。

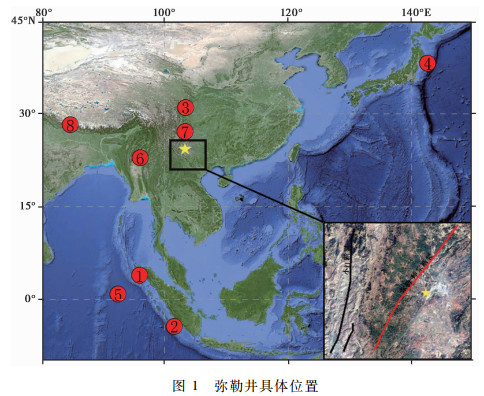
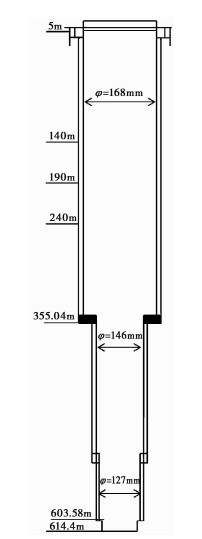
1 弥勒井概况

弥勒井位于弥勒-师宗活动断裂带附近(石云等，2013)，弥勒-师宗断裂为NE走向的走滑断层(图 1)。该井为自流井，流量约为116mL/s(唐彦东，2015)，井孔依次由直径168mm的套管、直径146mm的过滤管及127mm的过滤管组成，其中，直径168mm的套管和直径146mm的过滤管密封连接。井深614.4m，其表层0~5m为第四系覆盖层，由耕植土、冲湖积层夹碎石组成；5~140m为厚层状灰岩、白云岩，其中，102.16m以上裂隙、溶洞极为发育，与表层覆盖层一起构成潜水含水层；140~190m为页岩、泥质砂岩、粉砂岩3层，偶夹薄层泥质白云岩，为相对隔水层；190~240m为层状白云岩，偶夹粉、细砂岩，富水性较强，是承压含水带；240.0~614.4m为泥质页岩、含钙页岩，泥质及钙质粉砂岩、砂岩和薄层泥质灰岩、灰岩、白云岩互层，富水性较弱。下未见底，为非完整井。其中，含水层段为三叠系个旧组第二段，深度190~240m，观测井段为355.04~603.58m，与上覆含水层有一定水力联系(图 2)。

从2004年1月开始对该井进行数字化观测，其中水位观测仪器为LN-3型数字化水位仪。自观测以来，仪器正常，观测数据连续且稳定，采样率为每分钟1次，收集2004年1月~2015年12月的原始水位数据，并对其进行预处理，去除由仪器异常引起的水位异常(锯齿、突变)数据。2008年12月对该井及其泄流口进行清洗，导致井水位有明显突升，水位影响一直持续到2009年10月。

2 潮汐理论 2.1 径向流潮汐参数关系

Hsieh等(1987)提出了在径向流条件下井水位对含水层压力水头响应模型，在引潮力作用下，井与井周含水层之间发生水流交换，当引潮力作用于含水层到井-含水层之间发生水流交换，会产生一个时间滞后，即相位差，因此相位差一般均小于0。在井-含水层响应模型基础上，Hsieh等(1987)推导出井水位压力水头振幅比A_r和相位差μ_r的计算公式

$ {A_{\rm{r}}} = {({E^2} + {F^2})^{ - 1/2}} $

(1)

$ {\mu _{\rm{r}}} = - {\rm{ta}}{{\rm{n}}^{ - 1}}\left({\frac{F}{E}} \right) $

(2)

其中

$ E \approx 1 - \frac{{\omega r_c^2}}{{2T}}{\rm{Kei}}({\alpha _\omega }) $

(3)

$ F \approx {\rm{ }}\frac{{\omega r_c^2}}{{2T}}{\rm{Ker}}({\alpha _\omega }) $

(4)

$ {\rm{ }}{\alpha _\omega } = {r_\omega }\sqrt {\frac{{\omega S}}{T}} $

(5)

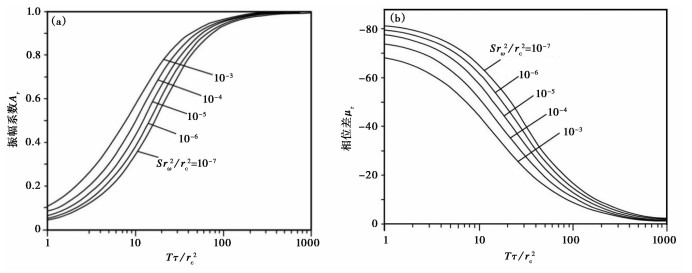
式中，A_r为径向流振幅系数，表示径向流条件下井水位波动振幅(数值上等于排水条件下水位波动振幅)与引潮力作用于含水层孔压(用水头表示)的扰动振幅(数值上等于不排水条件下水位波动振幅)的比值(廖欣等，2014)；μ_r为径向流条件下的相位差；ω为潮汐分波的频率；T为含水层导水系数，等于含水层渗透系数与含水层厚度的乘积；S为含水层贮水系数；r_ω为滤水管半径；r_c为井孔套管半径；Ker和Kei分别为开尔文函数的实部和虚部。式(1)~(5)表明，径向流振幅比A_r和相位差μ_r是关于导水系数T和贮水系数S的函数，计算振幅比A_r和相位差μ_r在不同Sr_ω²/r_c²值条件下，随Tτ/r_c²的变化(图 3)。

由图 3可知，在贮水系数一定的前提下，径向流振幅系数A_r随着Tτ/r_c²的增大而增大，径向流相位差μ＜0也随着Tτ/r_c²的增大而增大，由于τ/r_c²为定值，即振幅系数A_r和相位差μ均随着导水系数T的增大而增大；在导水系数一定的前提下，径向流振幅系数A_r随着Sr_ω²/r_c²的增大而增大，径向流相位差μ也随着Sr_ω²/r_c²的增大而增大，同样，r_ω²/r_c²为定值，即振幅系数A_r和相位差μ均随着贮水系数S的增大而增大。由此可知，在径向流条件下，振幅系数A_r与相位差μ同向变化。

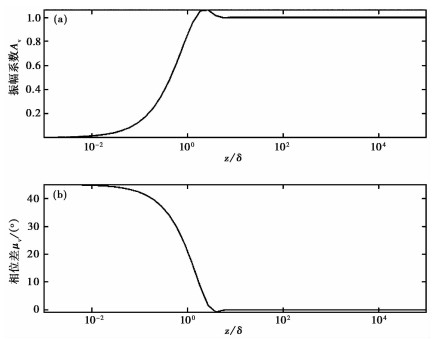
2.2 垂向流潮汐参数关系

对于承压井-含水层，当观测含水层上下岩石力学特征有差异时，在引潮力作用下2层的潮汐应变不同，在压力差驱动下将会产生水流交换；当承压井为非完整井时，含水层与其下伏地层可能会发生水流交换。这2种情况下产生的垂直方向上的水流交换简称垂向流。Roeloffs(1996)对潮汐垂向流进行了研究，计算表明M₂波潮汐相位一般为正值。在此基础上，Doan等(2006)研究了在只有垂向流条件下，潮汐参数垂向振幅系数和垂向相位差与含水层弥散系数的变化关系(图 4)，并提出其数学模型(Doan et al，2006；Wang et al，2018)。

$ P\left({z, \omega } \right) = B{K_{\rm{u}}}\varepsilon \left({1 - {{\rm{e}}^{ - \frac{{\left({1 + i} \right)z}}{\delta }}}} \right) $

(6)

$ {\rm{ }}{A_{\rm{v}}} = \left| {\frac{P}{{B{K_{\rm{u}}}\varepsilon }}} \right| = \left({1 - {{\rm{e}}^{ - \frac{{\left({1 + i} \right)z}}{\delta }}}} \right){\rm{ }} $

(7)

$ {\mu _{\rm{v}}}{\rm{ = arg}}\left| {\frac{P}{{B{K_{\rm{u}}}\varepsilon }}} \right| = {\rm{arg}}\left({1 - {{\rm{e}}^{ - \frac{{\left({1 + i} \right)z}}{\delta }}}} \right) $

(8)

式中，A_v为垂向振幅系数；μ_v为垂向相位差；P为引潮力作用下的压力；K_u为不排水体积模量；B为Skempton系数；ε为体应变，$\delta = \sqrt {\frac{{2D}}{\omega }} $；D为含水层弥散系数；z为井口至滤管深度。

由图 4可得，振幅系数A_v随着弥散系数的增大逐渐增大，达到一定数值后保持不变；相位差μ_v随着弥散系数的增大逐渐减小，达到一定值后持续不变。因此可知，在一定范围内，垂向流条件下振幅系数A_v与相位差μ_v呈反向变化。

2.3 弥勒井径混合流模型

大多数的井-含水层都是以混合流类型存在的，对于井周围含水层中的每一点水流运动方向均可以分解为径向流和垂向流2个方向。

图 5为弥勒井-含水层水流运动方向结构图。根据弥勒井的水文地质条件及其构造图可知，观测含水层与其上覆含水层以及下伏地层均会产生水流交换，表明弥勒井的垂向裂隙很发育。与前人的研究(石云等，2013；刘春平，2017)一致，弥勒井是以垂向流为主、径向流为辅的混合流井。

3 弥勒井井水位与潮汐响应特征分析 3.1 井水位同震响应特征分析

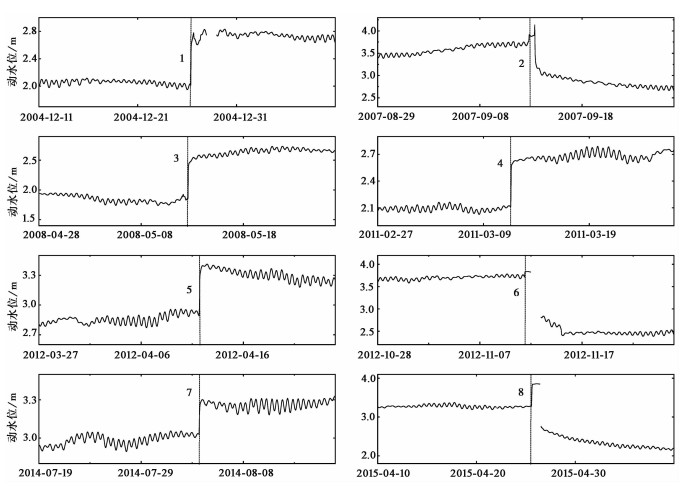
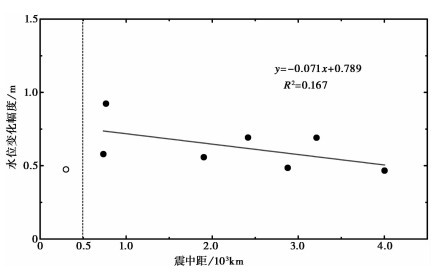
选取2004~2015年地震前后15天的水位变化数据(图 6)，分析其同震响应形态及水位变化特征(表 1)。结果显示：①水位同震响应形态上，弥勒井对地震的响应主要以阶变(阶升、阶降)为主(兰双双等，2011)。根据弥勒井观测日志记载，2012年11月9日17时、23时数据缺失，12时、14时数据突跳，预处理为缺数，水位动态下降；地震8(尼泊尔8.1级地震)水位阶变上升，井水溢出，26日10时15分被迫加大泄流量使水位恢复到可观测范围，将11、12时无效数据处理为缺数；因此根据水位记载变化趋势推测，地震6水位缓慢下降，地震8水位阶升后又缓慢下降。②水位变化幅度上，震中距与水位变化幅度可能存在一定的线性关系(图 7)。由图 7可知，在震中距大于500km时，震中距与水位变化幅度存在一个明显的负相关关系；在震中距小于500km时，由于统计的同震数据较少，不足以判断其相关性。当然，水位变化幅度还可能与地震的震级以及地震波能量密度等有一定的关系，仍有待于进一步研究。

3.2 潮汐响应的特征分析

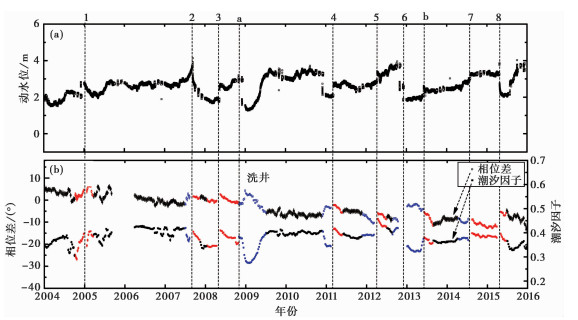
基于井水位潮汐变化，通过baytap-G软件，采用小时值的水位数据，取计算窗长为720hr(30天的观测资料)，滑动步长为168hr(7天的观测资料)(晏锐等，2012)，计算了M₂潮汐分波的潮汐因子(各个谐波的观测振幅与理论振幅之比)和相位差(潮汐的实测相位与理论相位之差，假设理论相位为零)及其误差值，并绘制了随时间的变化曲线(图 8)。

图 8为弥勒井的原始水位、M₂波潮汐因子和相位差随时间变化曲线，经查阅弥勒井的观测日志得知，在点a处对井进行了清洗，在点b处改造泄流装置。

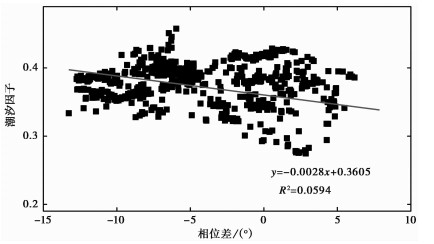
该井所反映出来的主要特征是井水位呈上升趋势，相位差由起初的大于零逐渐下降到小于零，很明显呈逐渐下降的趋势，表明该井渗透系数在逐渐减小，井-含水层常年处于堵塞的状态。在径向流条件下，随着渗透系数的增大，相位差和潮汐因子均逐渐增大，在垂向流条件下，随着渗透系数的增大，相位差逐渐增大，潮汐因子逐渐减小。因此，对于弥勒井(混合流井)来说，随着渗透系数的减小，潮汐因子在2种水流类型共存的情况下相抵消，即变化平稳。图 9为去掉同震时刻的相位差和潮汐因子的关系图，从图 9可得知，潮汐因子与相位差呈负相关关系，表明两者反向变化，与弥勒井的潮汐水流类型是以垂向流为主、径向流为辅的判断一致。但相位差有大于0，也有小于0，因此表明，在以垂向流为主的井-含水层中，相位差并非全为正值，与前人(Wang et al，2018)研究结果一致。相位差很明显呈逐渐下降趋势，可推断出图 8中潮汐因子呈微上升趋势。地震1、3、8震前和震后潮汐因子和相位差均同向变化，地震2、4、5、7震前潮汐因子和相位差反向变化，震后潮汐因子和相位差同向变化，地震6潮汐因子和相位差均反向变化。图 8中a点处对井孔泄压流量进行校测与调整，并更换了球阀，同时对泄流管进行了清洗，水位下降后又逐渐恢复，潮汐因子和相位差发生了明显的反向变化，持续影响到2009年底。b点处改造泄流装置，导致水位突升。b点前潮汐因子和相位差反向变化，b点后潮汐因子和相位差同向变化。对于井水位同震响应形态与潮汐因子和相位差的主要特征详见表 2。

对于地震1、3、8，地震前后潮汐因子和相位差均同向变化，表明水流运动方向以径向流为主，垂向流为辅；对于地震2、4、5、7，地震前潮汐因子和相位差反向变化，地震后潮汐因子和相位差同向变化，以及b(人工改造)前潮汐因子和相位差反向变化，b后潮汐因子和相位差同向变化，表明水流运动方向以径向流为主变为以垂向流为主，且地震1、2、3、4、5、7、8及点b水位变化形态都是以阶变型为主(阶升、阶降)。对于地震6，地震前后潮汐因子和相位差均反向变化，表明水流运动方向以垂向流为主，其水位变化形态主要为缓降。表 2中的地震波能量密度是根据前人(Wang et al，2010；Manga et al，2007)推导的地震波能量密度e与震中距r和震级M之间如下的经验公式计算获得

$ {\rm{lg}}\mathit{r} = 0.48M - 0.33{\rm{lg}}e - 1.4 $

(9)

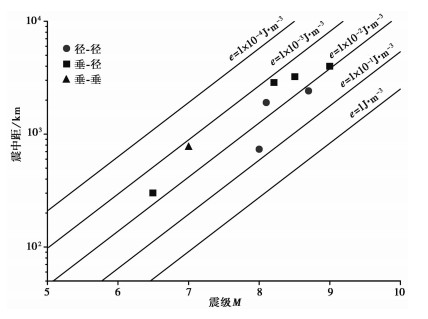
这一关系是利用美国南加利福尼亚的地震数据得出的，由于目前没有基于国内场地的相关数据，在没有更好关系的情况下，我们借用该经验公式作为近似值。利用式(9)进行震级、震中距与地震波能量密度关系分析，做出弥勒井震级、震中距的对数图(图 10)，确定不同地震的能量值。坐标轴中的直线代表不同震级与震中距对应的地震波能量密度。由图 10可知，震级一定时，地震波能量密度与震中距呈负相关；震中距一定时，地震波能量密度与震级呈正相关。从同震引起弥勒井井水位M₂波潮汐因子和相位差变化的几次地震中震级、震中距以及地震波能量密度关系上看，引起潮汐因子和相位差变化的地震波能量密度下限为10^-3J/m³，与Wang等(2010)研究结果一致。Wang等(2010)在研究地震波能量密度与震级、震中距之间关系时，认为地震波引起含水层渗透系数变化的能量密度下限约为10^-4J/m³，当地震波能量密度大于10^-3J/m³时，地震波对裂隙的剪切作用会更强，从而能更显著地引起含水层渗透系数的变化。从图 5可以看出，水流运动类型从垂向-径向、径向-径向的地震的地震波能量密度均较大一些，水流运动类型为垂向-垂向的地震的地震波能量密度较小一些。表明当地震波能量密度足够大时，可以使水流运动类型本以垂向流为主转变为以径向流为主，以径向流为主的仍以径向流为主；当地震波能量密度不够大时，水流运动类型本以垂向流为主的仍以垂向流为主。

弥勒井是一口非完整井，它的观测含水层不仅与上层含水层有一定的水力联系，与下伏地层也有一定的水流交换，它的垂向裂隙较发育。对于地震2、4、5、7，地震前潮汐因子和相位差呈反向变化，表明水流运动方向以垂向为主；地震后，潮汐因子和相位差呈反向变化，表明水流运动方向发生了变化，由垂向流变为径向流。对于地震1、3、8，地震前后潮汐因子和相位差均呈反向变化，表明地震前后水流运动类型一直为以径向流为主，地震只是改变了含水层渗透系数的大小，却没有改变其水流运动方向。对于地震6，地震前后潮汐因子和相位差均呈反向变化，表明地震前后水流运动类型一直为垂向流，同样，地震只是改变了渗透系数，没有改变水流运动方向。观察这些地震的地震波能量密度(表 2、图 10)，地震6的地震波能量密度最小，其它地震的地震波能量密度均较大。由此表明，在弥勒井本身以垂向流为主的前提下，在地震发生前，当水流运动方向为垂向流时，地震发生后并以地震波的形式传播到井-含水层，地震波传播对含水层产生剪切作用，产生的剪切力作用于含水层水平裂隙，导致裂隙中的胶粒物质得到了疏通和迁移，当地震波能量足够大时，致使水流运动类型发生改变，由以垂向流为主变为以径向流为主(如地震2、4、5、7)。在地震发生前，水流运动类型为径向流时，地震发生后，如果地震波能量密度足够大，地震波作用于裂隙介质的水平剪切力会使裂隙介质中胶体物质等得到更强的疏通和迁移，致使含水层渗透系数增大，从图 8可以看出在地震前后水流运动类型为径向流时，震后相位差均增大，渗透系数增大(如地震1、3、8)；在地震发生前，水流运动类型为垂向流时，地震发生后，如果地震波能量没有达到使含水层水流运动类型发生改变，地震只是改变了含水层渗透系数，震后相位差增大，渗透系数增大，没有改变含水层水流运动方向，震后水流运动方向仍是以垂向流为主，径向流为辅。对于a事件(洗井)，洗井前水流运动方向以径向流为主，对井清洗后，垂向裂隙得到了足够的疏通，水流垂向运动明显；对于事件b(改造泄流装置)，水位突升，b点之前水流运动类型以径向流为主，b点后水流运动类型以径向流为主。表明水位突升产生的能量足够大，致使含水层水平裂隙介质得到疏通，改变了水流运动方向。

4 结论与展望

(1) 地震波对近场和远场都有明显的影响作用，弥勒井对地震波的同震响应主要以阶变(阶升、阶降)为主，震中距大于500km的地震的同震响应幅度与震中距存在一定的线性关系。

(2) 在弥勒井井水位水流运动类型本身是以垂向流为主的前提下，当震前水流运动类型为垂向流，若地震产生能量足够大，地震波作用于径向含水层，使含水层水流运动类型由垂向变为径向；若地震产生能量不够大时，地震波作用于含水层不足以改变其水流运动方向，只是改变了含水层渗透系数，水流运动类型仍以垂向流为主。当震前水流运动类型为径向流时，地震波作用于径向含水层，使径向含水层渗透系数更大，水流运动类型仍以径向流为主。

(3) 自然因素(地震)和人工因素(洗井、改造泄流装置)均可改变含水层水流运动方向和含水层渗透系数。当一些自然因素或人为因素使井水位发生突变，产生的能量足够大时，含水层渗透系数发生改变，通过计算潮汐参数之间关系可知改变的渗透系数的方向(径向、垂向)，基于径向井-含水层响应模型(Hsieh et al，1987)、垂向井-含水层响应模型(Doan et al，2006)便可精确计算径、垂向含水层渗透系数，对水资源绿色开发与利用提供了一定的帮助。

(4) 地震引起径向或垂向含水层渗透系数变化的原因不仅仅是由地震波作用于含水层引起的，还可能与当地井-含水层的岩性、水动力条件以及其他影响因素有关，这有待于进行深入研究。

致谢: 审稿专家提出宝贵的修改意见，中国地震台网中心刘春国副研究员在文章成稿前给予思路上的指导，路彤绘制了部分图件，在此一并表示感谢。