2. 湖北省地震局, 武汉 430070;
3. 中国地震局第二监测中心, 西安 710000
2. Hubei Earthquake Agency, Wuhan 430070, China;
3. The Second Monitoring Center, China Earthquake Administration, Xi'an 710000, China
由于受西部印度-欧亚板块碰撞和东部太平洋板块俯冲作用,中国大陆内部强震频发、地震灾害严重(邓起东等,2002;陈颙等,2005;张培震等,2013)。因此,积极开展包括地震监测预报在内的防震减灾工作、最大限度减轻地震灾害是我国的基本国策,我国也是全球唯一以政府行为长期开展以减灾为目标的地震监测预报工作的国家(江在森等,2005;刘桂萍,2006;邵志刚等,2017)。
流动重力观测是地震监测预报的重要技术方法之一。早在1964年日本新潟、美国阿拉斯加等地震前后即观测到了重力变化(Fujii,1966;Barnes,1966)。我国自1966年邢台大地震后开始开展地震流动重力监测工作,并观测到了1975年海城7.3级、1976年唐山7.8级地震前后重力变化异常(卢造勋等,1978;陈运泰等,1980;李瑞浩等,1987)。近年来,利用流动重力观测资料,中国地震局重力学科专家对2014年云南鲁甸6.5级、2016年青海门源6.4级、2016年新疆呼图壁6.2级、2017年四川九寨沟7.0级等强震均进行了较好的年度、年中预测(祝意青等,2018)。
尽管前人早已观测到震前重力变化,且先后提出过质量迁移、膨胀扩容、闭锁剪力等“模式”用于解释震前重力场变化(陈运泰等,1980;李瑞浩等,1987;申重阳等,2011),但是,受地球内部的“不可入性”、大地震的“非频发性”、地震物理过程的复杂性等困难的制约(陈运泰,2009),地震预报还处于经验预报阶段。因此,从实践中不断总结经验,再应用于指导地震监测预报实践,是提高流动重力地震分析预报能力的重要方法。近年来,随着典型震例资料的积累,人们对地震孕育相关重力变化过程、范围、量级等逐步有了更多的认识。本文拟通过搜集相关文献资料,并结合笔者近年的流动重力地震分析预报实践工作,从实际震例中总结提炼地震孕育与重力变化异常之间的时空关系,尝试建立流动重力地震分析预报的定量依据。一方面有助于开展地震分析预报实践,另一方面也可作为未来发展物理预报方法的工作基础。
1 震前重力变化异常时变距S与量级G的定义地震学家指出,地震预测应同时给出未来地震的位置、大小、时间、概率4种参数(陈运泰,2009)。但是,受制于目前的科技水平,在实践层面,不同技术手段往往侧重于某一个或几个参数的预测评估。我国目前的流动重力观测复测周期为1~2期/年,主要应用于中长期、强震(≥6级)、危险区地点的分析,尤其是在危险区地点判定方面发挥了较好作用。
震例总结表明,强震孕育过程中经常可观测到重力变化的高梯度带、四象限等特征形态,且地震经常发生在高梯度带零值线或四象限图像中心附近。震级越大,孕震过程相关的重力变化范围和量级越大。一般发震时间、地点、震级与重力变化存在如下关系:
(1) 重力变化的空间分布特征与发震地点有关;
(2) 震前重力变化覆盖范围越大,则震级越大;
(3) 震前重力变化量级越大,则震级越大;
(4) 震前2~3年的观测对发震时间预测非常关键。
已有学者根据滇西地震预报实验场等区域震例资料,统计分析了震级与重力变化范围和量级之间的定量、半定量关系(贾民育等,1995、2000),并采用时变距S来描述重力变化异常范围。为保持关于震级与重力变化异常范围之间关系讨论的延续性,本文依然采用贾民育等(2000)对时变距S的定义,即时变距S为震中至正异常区中心的距离,是特征异常区的半径。由于本文收集的震例震中大多位于测网内部,能够识别较完整的重力变化异常图像,对时变距S再做如下两点说明:
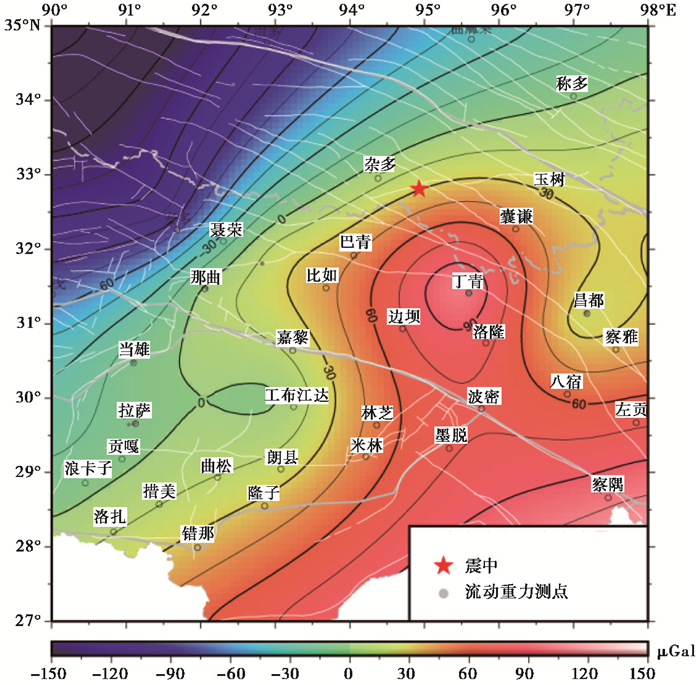
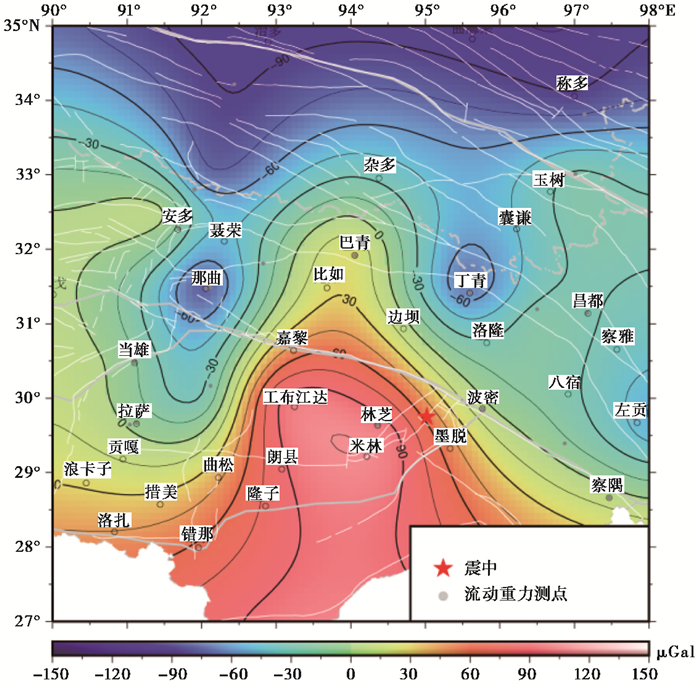
(1) 测网稀疏时,如图 1所示,2016年10月17日青海杂多6.2级地震时变距S取震中至重力变化最大点丁青的距离;或如图 2所示,2017年11月18日西藏米林6.9级地震时变距S取震中至其西部正变化显著点林芝和工布江达的距离平均值;
|
图 1 2016年10月17日青海杂多6.2级地震前重力变化(2010~2015年) |
|
图 2 2017年11月18日西藏米林6.9级地震前重力变化(2015~2017年) |
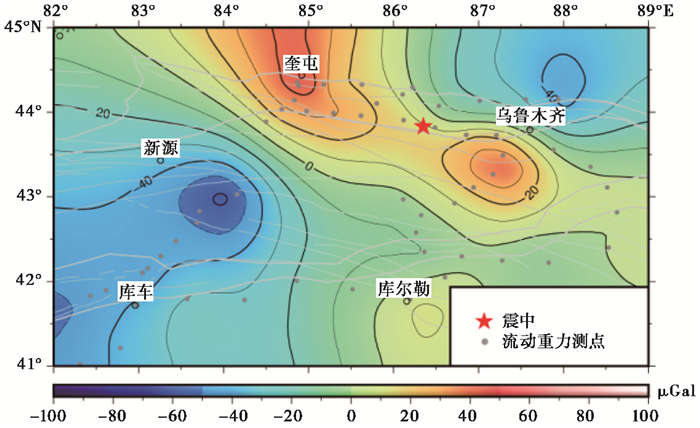
(2) 重力异常变化出现四象限图像时,如图 3所示,2016年12月8日新疆呼图壁6.2级地震时变距S为震中至2个正变化中心距离的平均值。
|
图 3 2016年12月8日新疆呼图壁6.2级地震前重力变化(2015年9月~2016年5月) |
重力变化异常量级G定义为地震、断裂构造运动相关重力变化差异:
(1) 重力变化异常图像出现梯度带和四象限特征时,取正负变化的最大差值;
(2) 仅有局部重力变化时,取最大变化值(如图 1,取丁青点变化值为90μGal);
(3) 由于强震前一般有较长时间的重力场演化过程,而流动重力观测时间间隔较长,无法确定哪一期观测到的重力变化异常最具代表性,因此当某地震有多期变化值时,取累计变化较为显著时期平均值作为G值(祝意青等,2018)。
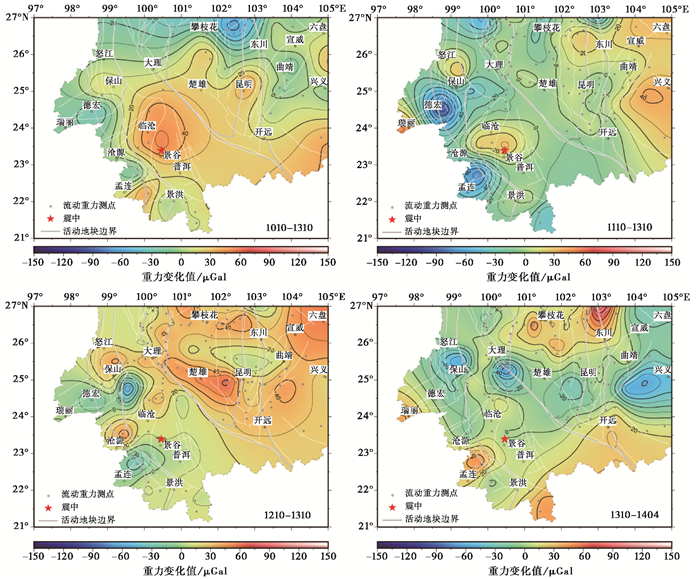
以2014年10月7日云南景谷6.6级地震为例,说明本文重力变化异常时变距S和量级G的确定过程。如图 4所示,震前重力变化过程如下:
|
图 4 2014年10月7日云南景谷6.6级地震前重力异常变化 |
(1) 1010-1310(表示2010年10月~2013年10月期间的重力变化,下同),滇西南地区重力变化梯度带在德宏-沧源-景洪一带与龙陵-澜沧断裂走向一致,震中核心区域正重力变化半径约113km,震中西南部重力变化差异约60μGal;
(2) 1110-1310,震中西南形成了南负-北正的重力变化梯度带,正变化区域半径约75km,重力变化差异约100μGal;
(3) 1210-1310,震中西南形成了垂直于龙陵-澜沧断裂的梯度带,震中至正重力变化中心距离约110km,重力变化差异约60μGal;
(4) 1310-1404,半年期重力变化显示,震中西南部有局部正重力变化异常,震中至正重力变化中心的距离约101km,重力变化差异约40μGal。
因此,景谷6.6级地震重力变化时变距S和量级G为上述前3个时段的平均值,即S约为100km、G约为73μGal。
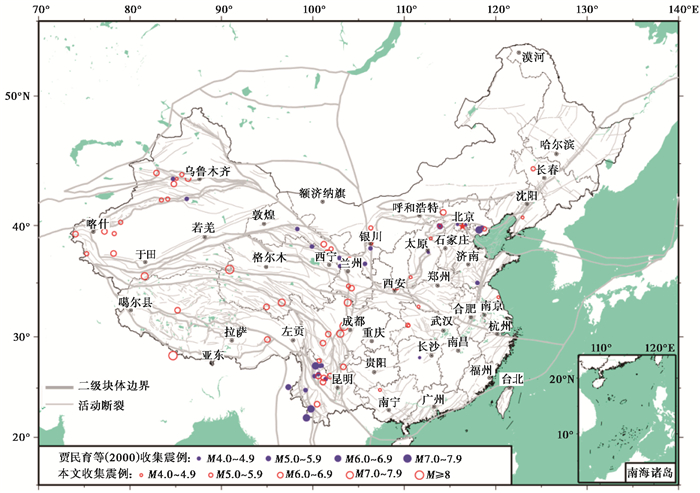
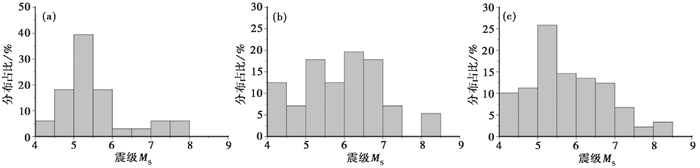
2 时变距S及量级G与震级MS间的关系 2.1 震例收集根据公开发表文献和中国地震局重力观测技术管理部总结,本文统计了56个震例对应的重力变化时变距S和量级G(表 1)。表 1中56个震例的空间分布见图 5。从图 5可以看出,表 1震例主要覆盖南北地震带、天山地震带,加上贾民育等(2000)给出的震例,对我国主要地震带形成了较好的覆盖。从震级分布看,贾民育等(2000)收集的4级以上震例共33个,其中5~6级占近60%(图 6(a))。本文增加了大量6级以上地震,56个震例中,5~6级地震约占40%,6~7级地震约占37.5%,从震级分布上更均衡(图 6(b))。
| 表 1 4级以上地震及其重力变化时变距S与变化量级G |
① 申重阳, 2017, 流动重力理论基础与地震预测研究实践。
|
图 5 贾民育等(2000)收集震例与本文统计震例空间分布 |
|
图 6 贾民育等(2000)收集震例(a)、本文统计震例(b)及全部震例(c)震级频率分布直方图 |
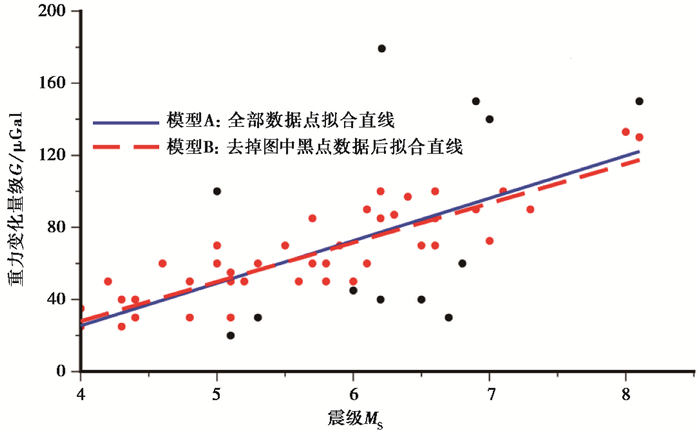
地震是岩石能量积累到突破其强度后,能量突然释放的结果。一般震级越大,则震前能量累积越多,孕震过程中岩石的形变、物质的迁移等规模也越大。因此,震级越大,可能意味着震前重力变化异常量级越大。图 7为重力变化量级G与震级MS间的关系。统计表 1中56个震例重力变化量级G与震级MS之间的关系,发现两者呈线性相关,相关度达0.682,线性拟合得出
| $ G = 23.56{M_{\rm{S}}} - 68.75 $ | (1) |
|
图 7 重力变化量级G与震级MS间的关系 |
拟合直线见图 7中蓝色实线(模型A)。去掉G与直线拟合结果之差大于1倍中误差的震例后,剩余44个震例,则G与MS之间线性相关度可达0.86,线性拟合得出
| $ G = 21.82{M_{\rm{S}}} - 59.37 $ | (2) |
拟合直线见图 7中红色虚线(模型B)。
根据式(1)、(2),可对4~8级地震对应的重力变化量级G作出评估(表 2)。从表 2可以看出,5、6、7、8级地震对应的震前重力变化异常量级分别为50、70、90、120μGal,与祝意青等(2018)的总结基本一致。
| 表 2 不同震级地震对应的震前重力变化异常量级G(单位:μGal) |
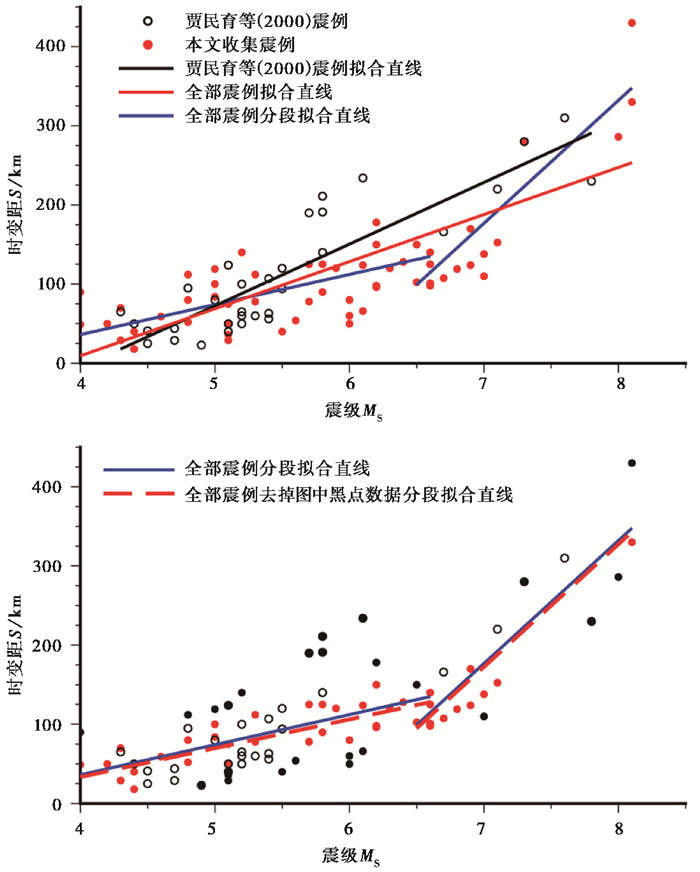
综合贾民育等(2000)和表 1中的震例,共计获得4级以上地震震例89个,图 8为根据全部89个震例分析的震级与时变距的关系(分段拟合),分析发现时变距S与震级MS之间线性相关度达0.778,线性拟合得出
| $ S = 59.49{M_{\rm{S}}} - 228.55 $ | (3) |
|
图 8 根据全部89个震例分析的震级与时变距的关系(分段拟合) |
拟合直线见图 8中红色实线。
图 8中黑色直线为贾民育等(2000)分析结果,其5.5~6级左右地震时变距S明显大于本文震例。从图 8可以看出,7级以上地震时变距S一般位于拟合直线的上方,意味着大地震时变距S增长更快。以6.5级地震为界,对MS与S之间关系进行分段统计。对所有89个震例分段线性拟合可得出
| $ \left\{ {\begin{array}{*{20}{l}} {S = 37.99{M_{\rm{S}}} - 115.69, {M_{\rm{S}}} \le 6.5}\\ {S = 155.31{M_{\rm{S}}} - 910.38, {M_{\rm{S}}} > 6.5} \end{array}} \right. $ | (4) |
拟合图像见图 8中蓝色实线。剔除偏差大于1倍标准差的震例后,尚余69个震例,分段拟合可得出
| $ \left\{ {\begin{array}{*{20}{l}} {S = 36.38{M_{\rm{S}}} - 112.06, {M_{\rm{S}}} \le 6.5}\\ {S = 154.89{M_{\rm{S}}} - 911.6, {M_{\rm{S}}} > 6.5} \end{array}} \right. $ | (5) |
拟合图像见图 8中红色虚线。
从图 8可以看出,时变距S随着震级增大而增大,特别是震级在6.5级以上时,时变距S增长更快。这与震级越大则能量积累越多,对应的孕震范围越大这一基本认识一致。根据上述统计公式(3)~(5),可评估不同震级对应的时变距S、重力变化异常范围及对测网覆盖范围的需求(表 3)。
| 表 3 重力变化时变距S、异常范围与震级MS之间关系统计 |
从表 3可以看出,震级为5、6、7、8级时,时变距S分别为72、109、175、330km。本文计算的6、7级地震时变距略小于贾民育等(2000)的计算结果。由于本文增加了较多的6~7级震例,且震中一般位于测网内部,观测到了较完整的震前重力场演化过程,因此本文的分析结果更为全面。震级为5、6、7、8级时,对应的重力变化异常范围分别约为140、220、350、660km,与祝意青等(2018)的总结基本一致。
3 讨论本文从地震分析预报实践需求出发,通过震例总结提炼震前重力场变化的定量指标,为分析预报实践、重力测网建设、重力场变化机理建模等提供基础数据。
(1) 对几个小震前重力变化的说明
表 1中肃南-门源交界5.1级地震(地震18)重力变化20μGal,及地震39、40、53、54等几个地震前重力变化也仅有20~30μGal,笔者将其列入统计,原因为:
① 虽然上述小地震的重力变化与流动重力观测精度为同等量级,但是,这些地震周围重力变化的区域特征明显。即,判断是否异常,往往不能简单根据误差理论去统计其量级,还应看整体重力变化区域特征。其原因为,如果按误差理论,误差随机分布,那么重力场变化图像在仅有误差的情况下不会呈现区域特征。
② 从分析预报的实践来看,小于5级的地震预报意义不大,本文将其纳入统计,主要是为了拓展统计边界,使5级以上地震对应的重力变化量级范围更清晰。
③ 从图 7、表 2的统计结果来看,纳入这几个地震后的统计结果没有出现大的离散(即没有导致统计线性关系的大幅偏离)。
此外,肃南-门源交界5.1级地震(表 1中地震18)重力变化20μGal、肃南5.0级地震(表 1中地震47)重力变化100μGal。这2个地震地点邻近、震级相近,但重力变化量级却差别很大,是表 1中5级左右地震重力变化统计的特例,出现这种差异的原因与测网分布、观测过程等均相关(梁伟锋等,2010;祝意青等,2016)。本文在表 2中的统计模型B中已将二者剔除,对最终统计结果影响不大。
(2) 流动重力观测技术的地震重力变化检测能力
当前,我国流动重力观测采用“绝对重力控制下的相对重力联测”方法。绝对重力观测采用实测精度为5μGal的FG5型绝对重力仪和实测精度为10μGal的A10型绝对重力仪。相对重力联测采用重复性为10μGal的CG5、LCR和Burris型相对重力仪,且采用A→B→C→……→C→B→A往返双程测量方法,以控制仪器漂移等产生的影响。实际作业中,流动重力观测能达到10~20μGal的精度(华北、南北带、东南沿海及新疆天山等重点监视区的观测精度能达到10μGal左右;青藏高原地区观测精度能达到20μGal以内),结合表 2中重力场变化量级的总结,认为当前的观测技术在理论上具备检测5级以上地震相关重力变化异常的能力。
(3) 震前区域性重力变化异常的意义
一般情况下,地震前兆所位于的地震孕震区是破裂尺度的2~3倍(刘杰等,2016)。孙银涛等(2016)统计分析了中国大陆地震震级与破裂长度之间的关系。若取孕震范围为破裂长度的3倍,则5、6、7、8级地震对应的孕震范围(地震孕育的“源”区)分别约为10.5、42、174、705km。除8级地震外,其他震级对应的孕震范围明显小于本文估算的重力变化异常范围(表 3),这是因为强震是在大构造活动背景下的局部断层差异化运动,造成局部应力积累突破岩石强度后会突然失稳破裂,其孕育的力学演化过程不局限于发震断层。因此,地震监测预报工作不仅要着眼于地震孕育的“源”,还应关注周边“场”的演化。流动重力观测获得的重力变化异常范围(“场”)大于根据破裂长度推算的孕震范围(“源”),恰恰说明“场”的演化对“源”起着重要作用。流动重力观测的是“场”兆,近年来在地震年度预测中主要作用于地点判定方面,是由“场”及“源”的体现。
4 结论本文通过震例总结,分析提炼了地震震级与重力变化异常范围和量级之间的统计关系,相关参数可作为地震分析预报、流动重力测网设计和测网监测能力评估等工作的定量依据。
一般情况下,地震预报的“时、空、强”与重力变化异常的“时、空、强”呈正相关,即重力变化异常的量级、范围越大,则对应震级越大,震级越大则震前重力场演化持续的时间可能越长,重力变化异常形态与未来发震地点密切相关。根据本文的分析,可得到如下结论:
(1) 5、6、7、8级地震震级判定的重力变化异常量级参考指标分别为50、70、90、120μGal,参见表 2;
(2) 5、6、7、8级地震震级判定的重力变化异常范围参考指标分别为140、220、350、660km,参见表 3;
(3) 以目前流动重力1~2期/年的复测周期,不能对震前重力场演化过程进行较详细跟踪,因此尚不能得出与时间的统计关系。
艾力夏提·玉山、李瑞、刘代芹等, 2017a, 2017年精河MS6.6地震前重力变化特征分析, 中国地震, 33(4): 749-756. |
艾力夏提·玉山、刘代芹、李杰等, 2017b, 2016年阿克陶MS6.7地震前后重力变化特征分析, 内陆地震, 31(2): 198-206. |
艾力夏提·玉山、刘代芹、李瑞等, 2017c, 2017年塔什库尔干MS5.5地震前重力变化特征分析, 大地测量与地球动力学, 37(增刊Ⅱ): 128-133. |
陈丽、刘代芹、李杰等, 2017, 新疆喀什及邻近区域流动地磁和流动重力联合分析研究, 震灾防御技术, 12(2): 423-432. |
陈颙、陈运泰、张国民等, 2005, "十一·五"期间中国重大地震灾害预测预警和防治对策, 灾害学, 20(1): 1-14. |
陈运泰, 2009, 地震预测:回顾与展望, 中国科学:D辑, 39(12): 1633-1658. |
陈运泰、顾浩鼎、卢造勋, 1980, 1975年海城地震与1976年唐山地震前后的重力变化, 地震学报, 2(1): 21-31. |
邓起东、张培震、冉勇康等, 2002, 中国活动构造基本特征, 中国科学:D辑, 32(12): 1020-1030. |
冯建林、檀玉娟、秦建增等, 2017, Cg-5重力仪一次项格值系数对宁夏重力场变化的影响, 大地测量与地球动力学, 37(3): 319-322. |
郝洪涛、李辉、孙少安, 2012, 华北地区流动重力观测资料的初步清理, 大地测量与地球动力学, 32(6): 54-58. |
郝洪涛、李辉、孙少安等, 2016, CG-5重力仪格值系数变化研究及应用, 大地测量与地球动力学, 36(增刊): 14-17. |
郝洪涛、李辉、张志坚, 2014, 岷县-漳县6.6级地震前后重力场变化, 大地测量与地球动力学, 34(3): 43-47. |
胡敏章、郝洪涛、宋浩等, 2019, 弱地震活动背景地区流动重力变化探析, 大地测量与地球动力学, 39(4): 339-343. |
黄健、詹景立、李爱霞, 2004, 雅江6.0级地震前后的重力变化异常特征, 四川地震, (1): 27-30. |
贾民育、邢灿飞、孙少安, 1995, 滇西重力变化的二维图象及其与5级(MS)以上地震的关系, 地壳形变与地震, 15(3): 9-19. |
贾民育、詹洁晖, 2000, 中国地震重力监测体系的结构与能力, 地震学报, 22(4): 360-367. |
江在森、任金卫、李志雄, 2005, 推进地震预测研究的战略对策问题, 国际地震动态, (6): 168-173. |
康开轩、李辉、刘少明等, 2015, 尼泊尔MS8.1地震前我国西藏及周边区域的重力长期变化, 大地测量与地球动力学, 35(5): 742-746, 757. |
李辉、申重阳、孙少安等, 2009, 中国大陆近期重力场动态变化图像, 大地测量与地球动力学, 29(3): 1-10. |
李瑞浩、陈益惠, 1987, 重力预报地震方法的实用性研究, 地震, (4): 60-62. |
李瑞浩、付兆珠, 1987, 唐山地震(M=7.8)前后的区域重力变化和扩容过程, 孙和平, 译, 内陆地震, 1(4), 426~434.
|
李子涛、梁放, 2003, 2002年6月17日海城4.0级地震前后重力场变化特征探讨, 东北地震研究, 19(3): 37-41. |
梁伟锋、祝意青、徐云马等, 2010, 2008年肃南5.0级地震前的重力变化, 大地测量与地球动力学, 30(2): 10-13. |
刘桂萍, 2006, 关于我国地震预报的几点思考, 国际地震动态, (3): 32-38. |
刘杰、张国民, 2016, "是否存在有助于预报的地震前兆"的讨论, 科学通报, 61(18): 1988-1994. |
刘善华、张鹤、李民, 2005, 滦县ML5.0地震前重力异常探讨, 大地测量与地球动力学, 25(1): 30-34. |
刘少明、孙少安、郝洪涛等, 2014, 湖北巴东MS5.1地震前的重力场变化, 大地测量与地球动力学, 34(3): 31-34. |
卢造勋、方昌流、石作亭等, 1978, 重力变化与海城地震, 地球物理学报, 21(1): 1-8. |
邵志刚、武艳强、江在森等, 2017, 中国大陆强震中期综合预测工作简介, 国际地震动态, (7): 14-23. |
申重阳、李辉、孙少安等, 2009, 重力场动态变化与汶川MS8.0地震孕育过程, 地球物理学报, 52(10): 2547-2557. |
申重阳、李辉、孙少安等, 2010, 2008年于田MS7.3地震前重力场动态变化特征分析, 大地测量与地球动力学, 30(4): 1-7. |
申重阳、谈洪波、郝洪涛等, 2011, 2009年姚安MS6.0地震重力场前兆变化机理, 大地测量与地球动力学, 31(2): 17-22, 47. |
苏树鹏, 2007, 张北6.2级地震及大同5.6级地震前的流动重力异常, 华北地震科学, 25(4): 55-58. |
苏树鹏、张纳莉、李菲等, 2008, 文安5.1级地震前的重力场变化, 华北地震科学, 26(2): 45-48. |
孙少安、郝洪涛、韦进, 2015, 云南景谷M6.6地震前重力场变化的区域性特征, 大地测量与地球动力学, 35(4): 613-615. |
孙银涛、徐国栋、龙海云等, 2016, 震级与破裂长度统计关系研究, 地震学报, 38(5): 803-806. |
王同庆、赵云峰、常金龙等, 2018, 东北地区重力场动态变化特征与前郭5.8级震群关系研究, 大地测量与地球动力学, 38(3): 249-253. |
王武星、石耀霖、张晶等, 2009, 河北文安5.1级地震前后重力场动态变化, 地震, 29(2): 40-47. |
谢汝一、秦建增、冯建林等, 2014, 山西原平4.2级地震前的重力场异常特征, 地震工程学报, 36(3): 639-644. |
徐云马、祝意青、程宏宾, 2008, 1998-2004年滇西地区重力场演化与MS ≥ 6.0地震, 大地测量与地球动力学, 28(2): 51-55. |
张培震、邓起东、张竹琪等, 2013, 中国大陆的活动断裂、地震灾害及其动力过程, 中国科学:地球科学, 43(10): 1607-1620. |
张永奇、丁晓光、曹建平等, 2017, 关中流动重力测网的中小地震映震能力分析, 地震研究, 40(2): 248-256. |
郑兵、王青华、罗海元等, 2015, 2012年宁蒗-盐源5.7级地震前的重力变化, 地震研究, 38(3): 370-376. |
祝意青、郭树松、刘芳, 2010, 攀枝花6.1、姚安6.0级地震前后区域重力场变化, 大地测量与地球动力学, 30(4): 8-11, 18. |
祝意青、胡斌、李辉等, 2003, 新疆地区重力变化与伽师6.8级地震, 大地测量与地球动力学, 23(3): 66-69. |
祝意青、胡斌、朱桂芝等, 2005, 民乐6.1级、岷县5.2级地震前区域重力场变化, 大地测量与地球动力学, 25(1): 24-29. |
祝意青、李辉、朱桂芝等, 2004, 青藏块体东北缘重力场演化与地震活动, 地震学报, 26(增刊): 71-78. |
祝意青、李铁明、郝明等, 2016, 2016年青海门源MS6.4地震前重力变化, 地球物理学报, 59(10): 3744-3752. |
祝意青、梁伟锋、湛飞并等, 2012, 中国大陆重力场动态变化研究, 地球物理学报, 55(3): 804-813. |
祝意青、梁伟锋、赵云峰等, 2017, 2017年四川九寨沟MS7.0地震前区域重力场变化, 地球物理学报, 60(10): 4124-4131. |
祝意青、刘芳、郭树松, 2011, 2010年玉树MS7.1地震前的重力变化, 大地测量与地球动力学, 31(1): 1-4, 8. |
祝意青、刘芳、李铁明等, 2015, 川滇地区重力场动态变化及其强震危险含义, 地球物理学报, 58(11): 4187-4196. |
祝意青、申重阳、张国庆等, 2018, 我国流动重力监测预报发展之再思考, 大地测量与地球动力学, 38(5): 441-446. |
祝意青、闻学泽、孙和平等, 2013, 2013年四川芦山MS7.0地震前的重力变化, 地球物理学报, 56(6): 1887-1894. |
祝意青、徐云马、梁伟锋, 2008, 2008年新疆于田MS7.3地震的中期预测, 大地测量与地球动力学, 28(5): 13-15, 132. |
祝意青、赵云峰、刘芳等, 2014, 新疆新源、和静交界6.6级地震前的重力变化, 大地测量与地球动力学, 34(1): 4-7. |
朱治国、艾力夏提·玉山、刘代芹等, 2017, 西天山地区重力场变化与地震研究, 大地测量与地球动力学, 37(9): 903-907, 922. |
Barnes D F, 1966, Gravity changes during the Alaska earthquake, J Geophys Res, 71(2): 451-456. DOI:10.1029/JZ071i002p00451 |
Feng J L, Wei J, Tan Y J, et al, 20016, Variation of gravity before the Alxa Zuoqi M5.8 earthquake, Geodesy Geodyn, 4(7): 295-301. |
Fujii Y, 1966, Gravity change in the shock area of the Niigata earthquake, Earthquake Ⅱ, 19(3), 200~216. Hao H T, Wei J, Hu M Z, et al, 2015, Temporal variation of gravity field prior to the Ludian MS6.5 and Kangding MS6.3 earthquakes, Geodesy Geodyn, 6(6), 429~436.
|
Okada Y, 1985, Surface deformation due to shear and tensile faults in a half-space, Bull Seismol Soc Am, 75(4): 1135-1154. |
 2019, Vol. 35
2019, Vol. 35


