0 引言

基于速率-状态依从摩擦定律，Dieterich(1994)将区域地震活动率分为稳定状态条件下(应力稳定释放)的背景地震活动率r及受到应力扰动变化的地震活动率两部分，并推导出总的地震活动率R与背景地震活动率r之间的关系。在一定假设条件下，上述应力扰动可由库伦应力变化表示(Dieterich，2000；Toda et al，2003、2005；Catalli et al，2008；仲秋等，2013)。基于这一理论和模型(以下简称R-S模型)，开展了一系列针对不同地震序列的回溯性预测研究(Toda et al，1998、2003、2005；Gross，2001；Parsons et al，2000；仲秋等，2013；贾若等，2014；米琦等，2015)。一般而言，模型可变参数主要有背景地震活动率r、背景应力加载速率$ {\dot \tau _r}$、状态参量Aσ以及余震持续时间t_a，普遍采用的数值拟合方法为Daley等(2003)给出的点过程状态下的对数最大似然函数法。

已有研究显示，无论是基于统计还是从物理角度分析，R-S模型中各参数存在着一定的相关性，即某一参数的变化会引起其他参数的变化，对模型预测结果也会产生一定的影响(Belardinelli et al，1999；Toda et al，2003；Gomberg et al，2005；Catalli et al，2008；Hainzl et al，2009；Cocco et al，2010；Woessner et al，2011)。但到目前为止，在详细考虑这些相关性后应如何针对特定序列来确定最优拟合方案的研究尚不多见。为探讨这一问题，本文以2013年吉林前郭5.8级强震群为例进行研究。根据某些特定参数的相关性，提出基于对数最大似然法的2种模型参数拟合方案：一是假定序列余震持续时间未知，即余震持续时间t_a非固定条件下的拟合；二是余震持续时间t_a固定条件下的拟合。基于对前郭震群余震目录的整理及统计分析，分别讨论了2种方案对该震群震后早期拟合的影响。

1 基本理论

Dieterich(1994)基于岩石力学实验结果及速率-状态依从摩擦定律，在地震成核理论的基础上，针对1个地震序列，建立了地震活动率与孕震区应力状态之间的定量关系

$ R = \frac{r}{{\gamma {{\dot \tau }_r}}} $

(1)

其中，r为背景地震活动率，表征区域稳定状态条件下的地震活动情况。$ {{{\dot \tau }_r}}$为背景应力加载速率，即稳定状态下的区域应力加载。这里所说的稳定状态，是指无应力扰动且应力稳定作用的状态。研究中通常假定背景地震活动率不随时间变化，但在一些大区域尺度的研究中要考虑随空间的变化(Toda et al，2005)。γ为状态变量，包括成核区域(即孕震断层面)的应力状态以及震源本身的固有状态，γ的微分表达式为(Dieterich，1994)

$ {\rm{d}}\gamma = \frac{1}{{A\sigma }}\left[ {{\rm{d}}t - \gamma {\rm{d}}\tau + \gamma \left({\frac{\tau }{\sigma } - \alpha } \right){\rm{d}}\sigma } \right] $

(2)

式中，τ为断层面上的剪切应力，A为与断面物理属性(如温度、压力)有关的固有状态参数，σ为正应力。通常将Aσ作为参数进行考虑，称其为“状态参数”。Dieterich(1994)给出，在$ {{{\dot \tau }_r}}$和σ为常数条件下，一次剪应力阶跃时γ的初值γ₀可表示为

$ {\gamma _0} = \frac{1}{{{{\dot \tau }_r}}}\exp \left({\frac{{ - \Delta \tau }}{{A\sigma }}} \right) $

(3)

假设应力阶跃前、后的应力加载速率恒定，根据式(1)、(2)、(3)可得一次剪应力阶跃后的地震活动率R对时间的函数

$ R(t) = \frac{r}{{1 + \left[ {\exp \left({ - \frac{{\Delta \tau }}{{A\sigma }}} \right) - 1} \right]\exp \left({ - \frac{{{{\dot \tau }_r}t}}{{A\sigma }}} \right)}} $

(4)

进一步研究发现，式(2)中等号右边的应力变化部分，即dτ-(τ/σ-α)dσ与库伦应力变化给出的形式相一致(Dieterich，2000；Toda et al，2003、2005；Catalli et al，2008；仲秋等，2013)。换言之，式(2)可进一步表示为

$ {\rm{d}}\gamma = \frac{1}{{A\sigma }}({\rm{d}}t - \gamma {\rm{dCFS}}) $

(5)

通过式(5)的引入，以包含有正应力信息的库伦应力阶跃代替了原有的剪切应力阶跃，以此作为模型的初始应力扰动。重复上述推导步骤，可以获得一次库伦应力阶跃ΔCFS后的地震活动率R(Catalli et al，2008)

$ R(t) = \frac{r}{{1 + \left[ {\exp \left({ - \frac{{\Delta {\rm{CFS}}}}{{A\sigma }}} \right) - 1} \right]\exp \left({ - \frac{{{{\dot \tau }_r}t}}{{A\sigma }}} \right)}} $

(6)

式中，r表示每平方公里每天发生的地震个数，$ {{{\dot \tau }_r}}$表示每天的应力加载量，ΔCFS和Aσ的单位为MPa。可见R实际上表征了单位面积、单位时间内的地震频次。因此，时间T、面积S内的地震总数N可表示为

$ N(T,S) = \int\limits_T {\int\limits_S R } (t,s){\rm{d}}s{\rm{d}}t $

(7)

利用R-S模型，已开展了多个地区的地震活动率的模拟研究(Toda et al，1998、2003、2005；Gross，2001；Parsons et al，2000；Catalli et al，2008；仲秋等，2013；贾若等，2014)。

式(6)中的库伦应力变化ΔCFS可由下式计算(King et al，1994；Harris，1998；Toda et al，1998、2003、2005)

$ \Delta {\rm{CFS}} = \Delta {\tau _{{\rm{rake}}}} + {\mu ^{'}}\Delta {\sigma _n} $

(8)

式中，Δτ_rake和Δσ_n分别为接收断层面滑动方向上的静态剪切应力变化和静态正应力变化(拉张为正)；μ′为视摩擦系数，包括孔隙流体和断层面上介质特性影响，一般取μ′为0.4~0.6(Okada，1992；King et al，1994；Toda et al，1998、2003、2005、2008)。由于基于静态库伦应力触发理论的余震活动研究较多，本文不再赘述。

利用上述模型对实际地震活动进行拟合的关键步骤及相关注意事项有：①确定研究区范围。所选研究区范围应尽可能地排除其他丛集活动的干扰，这就要求研究区范围不能过大，但过小的范围又会导致应力计算的不完全。通常情况下，对于同震库伦应力扰动而言，合适的研究区范围应在尽可能小的原则下，包含有全部0.01MPa以上的应力扰动区域及全部目标地震活动。②网格划研究区，计算同震库伦应力扰动。网格步长会影响计算效率、结果的精度。网格并非越小越好，应保证大部分网格内能够包含一定数量的地震活动。③利用每个网格内得到的应力扰动计算地震活动率，从而得到全区域地震活动率R随时间、空间的变化。④将理论值与实际值进行数值拟合，确定模型参数的最优解。

2 数据准备 2.1 震例简介及资料完备性分析

2013年10~11月，吉林松原前郭尔罗斯自治县发生5.8级强震群(以下简称前郭震群)，这是松辽盆地内部罕见的强震群型地震活动。根据防灾科技学院及松原市地震局项目研究结果^①，穿过震区的主要活动断裂有NE向的松原-肇东断裂、NW向的查干泡-道子井断裂以及平行于松原-肇东断裂并位于其北部30km附近的NE向克山-大安断裂，此次震群发生在NE向的松原-肇东断裂与NW向的查干泡-道子井断裂交汇地带。根据吉林地震台网记录，该震群在1个月的时间内先后发生5次5级以上地震，分别是10月31日M_S5.5和M_S5.0地震，11月22日M_S5.3地震以及11月23日M_S5.8和M_S5.0地震。截至2016年10月24日，共记录M_L＞0地震1353次，此后震区持续无震状态，直到2018年4月12日发生M_L3.6地震。据此可认为2013年前郭5.8级强震群余震活动在2016年10月24日前后已趋于结束，共持续约1089天。

① 沈军, 2012, 松原市活断层探测与地震危险性评价。

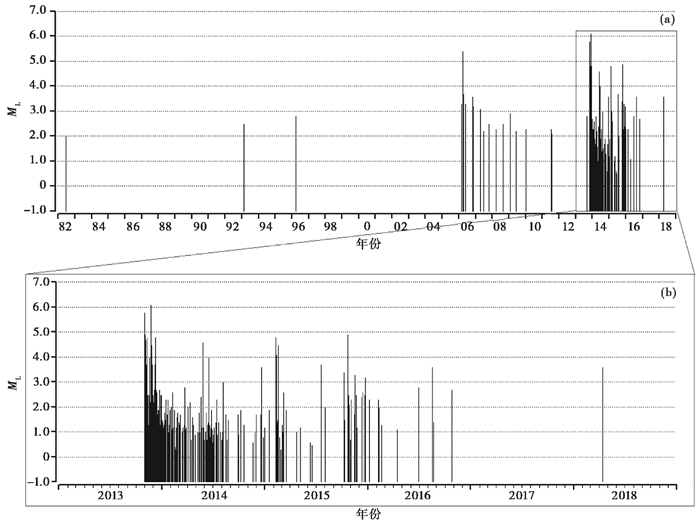
图 1为前郭震群2013年10月31日以来的余震活动及附近区域(44.3°~45.0°E，123.6°~124.8°N)1968年以来的历史地震分布，可见此次震群余震活动在空间上非常集中，基本分布在主震周围。对比附近区域1968年以来的历史地震活动(图 2(a))，前郭震群强震多且时间集中，伴随后续余震频次起伏衰减，多次主震具有多次应力触发特点(贾若等，2016)。

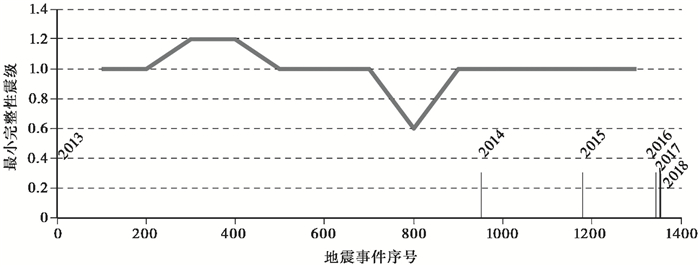
利用最大曲率法MAXC确定前郭序列最小完整性震级M_C(Wiemer et al，2000)。MAXC方法获得的M_C非常接近序列非累积频次最高点对应的震级值，也对应序列开始偏离G-R关系的震级。图 3为前郭震群M_L＞0地震最小完整性震级随时间的变化(频次统计步长取100)，可见平均最小完整性震级在M_L1.0左右，因此下文中选择M_L1.0作为拟合震级下限，尽可能消除资料不完备对结果的影响。

2.2 震源机制解及同震库伦应力变化

基于速率-状态依从摩擦定律的余震活动率模拟，需要计算主震对震区产生的应力阶跃。如前所述，在一定假设条件下，这种应力阶跃可由同震库伦应力变化表示。本文使用Coulomb3软件(Toda et al，2003、2005、2008)，在弹性半无限空间中计算了前郭震群5次5级以上主震的同震库伦应力变化，并假定接收断层参数与主震破裂面参数一致。

不同机构^②③和研究人员(吴微微等，2014；刘俊清等，2017)分别给出前郭震群主震的震源机制解，本文按以下原则确定用于库伦破裂应力计算的震源机制解结果：一是尽量使用近震台网结果，二是结果与其他单位相差不大，三是5次主震参数尽可能来源于同一单位。最终确定2013年10月31日M_S5.5、11月M_S5.3、M_S5.8和M_S5.0地震震源机制采用CEAIGP结果，10月31日M_S5.0地震震源参数选用刘俊清等(2017)结果，5次地震用于库伦应力计算的震源机制解列于表 1。由于震群震源机制解一致性较高，因而接收断层统一采用5次主震震源参数的平均值：走向314°、倾角60°、滑动角30°。

② http://www.cea-igp.ac.cn/

③ https://www.usgs.gov/

依据余震精确定位(薛艳等，2015；张洪艳等，2015；刘俊清等，2017)以及野外地质考察，认为前郭震群主发震构造为NW向系列断裂，且多次主震可能存在类似的破裂机制。依据断层破裂尺度与震级的统计关系，计算同震破裂尺度(Wells et al，1994)

$ \begin{array}{*{20}{l}} {M = {a_1} + {b_1} \cdot \lg {\rm{SRL}}}\\ {\lg {\rm{RW}} = {a_2} + {b_2} \cdot M} \end{array} $

(9)

其中，SRL(surface rupture length)为沿断层面水平走向的最短破裂长度，RW(downdip rupture width)为沿断层面深度方向的最短破裂宽度。参数a_i、b_i数值对不同类型断层有不同的优势分布范围(Wells et al，1994)，由于5次5级地震多以逆冲及走滑为主，而逆冲断层的a₁、b₁统计值为4.78~5.22、1.06~1.38，a₂、b₂统计值约为-1.41~-1.81、0.38~0.44，本文选择多组a_i、b_i值进行破裂尺度试算，参考余震重定位结果，认为最接近余震展布尺度的破裂尺度最为合理，最终确定a₁=4.78、b₁=1.08；a₂=-1.61、b₂=0.41。结果显示，几次5级地震的平均破裂尺度在10km左右。

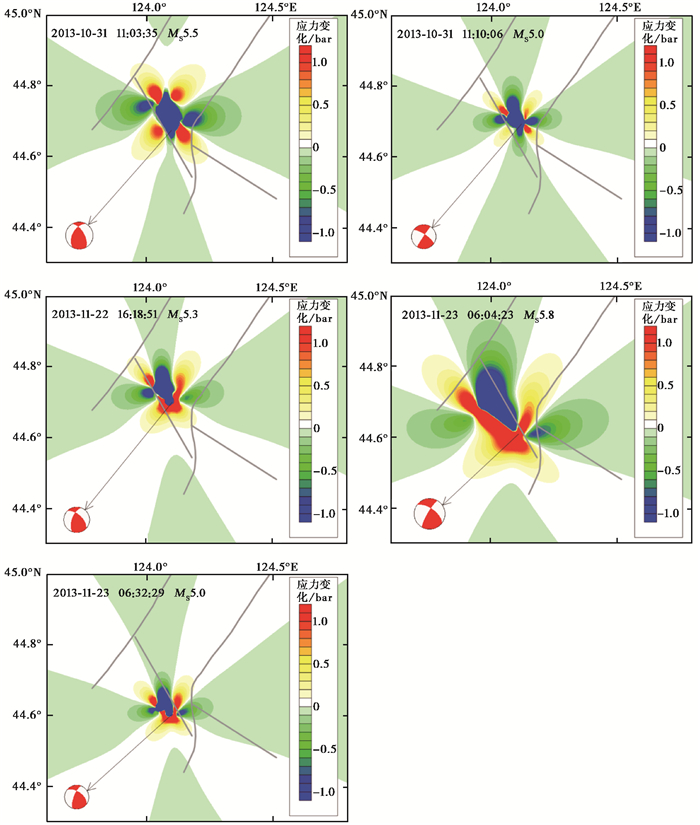
5次5级地震的同震库伦应力变化计算结果如图 4所示。计算中的视摩擦系数取为0.4，深度8km。可见11月23日M_S5.8地震的同震库伦应力扰动影响范围最大。根据所选定的接收断层参数，在破裂面附近的一些区域内，5次主震均产生了不同程度的应力卸载，即“应力影区”。在下文对地震活动率的拟合计算中，并未忽略这些“应力影区”的影响，因为负的应力阶跃会引起地震活动相对背景地震活动的降低(Dieterich，1994)。

3 模型参数拟合与余震活动率计算

根据式(6)可见，R-S模型中包含多个未知参数，若仅根据先验信息确定这些参数，在实际工作中会存在很大困难；而如果假定各参数完全相互独立，直接采用穷举法等进行数值拟合又会导致大量的循环计算，效率不高且还可能会因为多参数带来的多解性，出现收敛不稳定的情况。

根据以往研究，无论是基于统计实验还是物理推导，余震活动率模型参数间都存在一定的相关性(Hainzl et al，2009；Cocco et al，2010；Woessner et al，2011)。本文结合前人研究给出一些统计关系，首先通过先验信息确定一些基本参数，进而简化模型的可变独立参数为(r，Aσ)，然后进一步根据r和Aσ的相关性，提出2种基于对数最大似然法的数值拟合方式，一是考虑相关性的“余震持时t_a固定”条件下的拟合，二是不考虑相关性的“余震持时t_a不固定”拟合。下文以前郭5.8级震群为例，简要介绍这2种拟合方法，并在拟合效率、计算精度、结果可靠性、震例适用性等方面对比探讨二者的优劣势。

3.1 基本参数确定及最大似然拟合

式(6)中$ {{{\dot \tau }_r}}$表示背景应力加载速率，r表示背景地震活动率，分别代表某一地区在稳定状态条件下(应力扰动为0)的应力加载速率和平均地震活动率，r不包含区域范围内与应力扰动有关的丛集地震活动。根据式(6)，当ΔCFS=0时，地震活动率R=r。若假定余震活动为主震应力瞬时应力扰动导致的“丛集”地震活动，则余震活动率R_a=R-r。

研究显示，背景应力加载速率$ {{{\dot \tau }_r}}$与背景地震活动率r之间存在近似统计关系(Console et al，2006；Catalli et al，2008；Ward，1994)

$ {\dot \tau _r} \cong rM_0^*W_{{\rm{seism}}}^{ - 1}\frac{b}{{1.5 - b}}\left[ {{{10}^{(1.5 - b)\left({{m_{{\rm{max}}}} - {m_0}} \right)}} - 1} \right] $

(10)

式中，b为研究区长期背景地震活动的G-R关系比例系数，在历史地震资料丰富的地区可直接通过G-R关系拟合得到，若资料比较完备，一般不受震级上、下限影响。W_seism为孕震层厚度，对应于该地区地震活动可能达到的最大深度，由于松辽盆地浅源地震震源深度大多介于5~20km(高立新，2008；刘俊清等，2013；吴微微等，2014；薛艳等，2015；张洪艳等，2015)，因此本文取W_seism=20km。m₀和m_max分别为震级下限和上限，本文取m_max为序列最大地震震级M_L6.1，m₀为序列最小完备震级M_C=M_L1.0。M₀^*是震级为m₀的地震的地震矩，可由下式计算得到(Kostrov，1974；Kanamori et al，1975；Catalli et al，2008；Hainzl et al，2010)

$ M_0^* = {10^{9.1 + 1.5{m_0}}} $

(11)

显而易见，引入式(10)、(11)，可将R-S模型中的$ {{{\dot \tau }_r}}$由r的表达式替换，则未知参数简化为(r，Aσ)。对这2个参数的确定，本文采用对数最大似然拟合方法。根据Daley等(2003)的研究，时间段t₀~T内一次随机点过程的对数似然函数为

$ \ln L = \sum\limits_{{t_0} \le {t_i} \le T} {\ln } \lambda \left({{t_i}|\theta } \right) - \int_{{t_0}}^T \lambda (t|\theta){\rm{d}}t $

(12)

式中，t_i为地震事件的发生时刻，θ表示拟合参数向量，最优拟合的θ分布与最大lnL相对应。在本文中，λ为地震活动率R(或余震活动率R_a)，θ则为(r，Aσ)。

需要指出的是，通常情况下，背景地震活动率r和b一样，可通过历史地震活动资料确定，但在吉林前郭地区，由于历史地震活动弱、资料少，因而本文将背景地震活动率r和固有状态参数Aσ同作为需要拟合来确定的独立变量。同时，假定长时间尺度下的背景地震活动与序列在震级分布上具有近似特征，直接通过对余震活动的G-R关系拟合确定式(10)中b值，约为0.5。下文将进一步考虑r与Aσ的相关性，分2种情况进行拟合计算。选取用于拟合的实际观测资料为前郭震群10月31日~12月30日之间M_L＞1.0的全部余震活动。

3.2 余震持续时间非固定与固定条件下的拟合结果对比

根据Dietercih(1994)的研究，在状态参量Aσ确定、背景应力加载速率$ {{{\dot \tau }_r}}$恒定的条件下，余震持续时间t_a不依赖主震震级，可以表达为

$ {t_{\rm{a}}} = \frac{{A\sigma }}{{{{\dot \tau }_r}}} $

(13)

式中，$ {{{\dot \tau }_r}}$由式(10)确定。t_a的引入使Aσ、r具备了相关性。将式(10)、(13)联立后带入式(6)，有

$ R(t) = \frac{r}{{1 + \left[ {\exp \left({ - \frac{{\Delta {\rm{CFS}}}}{{{t_{\rm{a}}}{{\dot \tau }_r}}}} \right) - 1} \right]\exp \left({ - \frac{t}{{{t_{\rm{a}}}}}} \right)}} $

(14)

针对式(14)有2种拟合思路，一是不考虑这种相关性，直接与观测资料进行拟合，确定Aσ与r，进而利用式(13)计算t_a，称之为“余震持时非固定”条件下的拟合；二是考虑相关性，通过实际资料预先确定t_a，将Aσ用r表示，再进行拟合，称之为“余震持时固定”条件下的拟合。2种思路拟合结果的比较如下：

(1)“余震持时t_a非固定”条件下的拟合结果

此时有Aσ和r 2个可变参数，基于式(12)采用穷举法确定最优Aσ和r。首先要确定的是2个参数的拟合范围和搜索步长。

参考以往研究(Harris et al，1998；Toda et al，1998、2003；Guatteri et al，2001；Belardinelli et al，1999；Console et al，2006)，统计结果显示，Aσ一般分布在[0.0012，0.6]，本文取搜索范围为[0.001，0.6]，搜索步长0.001。

根据上文所述，前郭地区1978年以来的历史地震统计显示，所选研究区1978~2013年前郭震群发生前，共发生M_L＞1.0地震117次，则对应的该区平均历史地震活动率约为1.0×10^-6 d^-1km^-2。进一步考虑到历史地震资料的不完备，实际背景地震活动率r可能大于该量级。然而，当步长较小时，跨越多个数量级的搜索范围会使计算变得非常耗时。为了尽快找到r的精确拟合解，这里采用一种分步穷举的方案：首先分别在4个数量级下对r进行大步长的最大似然拟合搜索，分别为1.0×10^-6~9.0×10^-6，1.0×10^-5~9.0×10^-5，1.0×10^-4~9.0×10^-4，1.0×10^-3~9.0×10^-3，每个数量级下对应的搜索步长为分别为1.0×10^-n(n=6，5，4，3)，找到对数最大似然函数值的所在范围为1.0×10^-4~9.0×10^-4；然后，在该范围内，再取步长为0.1×10^-4进行拟合。

最终，得到最大对数似然函数值为1099.65，对应的r=1.1×10^-4d^-1km^-2，Aσ=0.006MPa。再根据式(10)和式(13)，计算得到余震持续时间t_a=435天，但这一结果与实际偏差较大。

(2)“余震持时t_a固定”条件下的拟合结果

如前所述，从实际资料来看，前郭震群自2013年10月31日开始至2016年10月24日基本结束，因而可粗略判定实际余震持续时间t_a=1089天，利用式(10)、(13)，此时未知参数只有r。同上文所述的对r的分步穷举搜索方案，得到最优结果r=1.0×10^-4d^-1km^-2，计算得到Aσ=0.0136MPa。对应的最大对数似然函数值1091.10。

对比上述2种条件下的拟合结果可见：

① 背景地震活动r差别不大，表明模型背景地震活动率受拟合资料影响不大；

② Aσ结果差异较大，余震持时t_a不固定条件下Aσ为0.006MPa，余震持时t_a固定条件下Aσ为0.0136MPa，二者近乎相差1个数量级。余震持时t_a不固定条件下计算得到的理论余震持续时间约为435天，与实际差异较大(实际余震活动持续时间约1089天)，因此当可以明确认定实际余震活动持续时间时，利用实际余震持续时间对模型拟合进行约束可能是有益做法；

③ 余震持时t_a不固定及固定2种条件下得到的lnL分别为1099.65、1091.10，进一步采用AIC方法(Akaike信息准则)对2种方法进行了综合判定：根据Akaike(1974)的研究，模型评价指标AIC=-2[lnL最大值]+2[参数个数]，AIC值越小，模型评价越好。计算得到t_a不固定AIC=-2195.3，t_a固定AIC=-2180.2。由此说明，对于震后早期(实际余震持时尚不能确定)而言，余震持续时间作为未知变量的拟合方式效果更好。

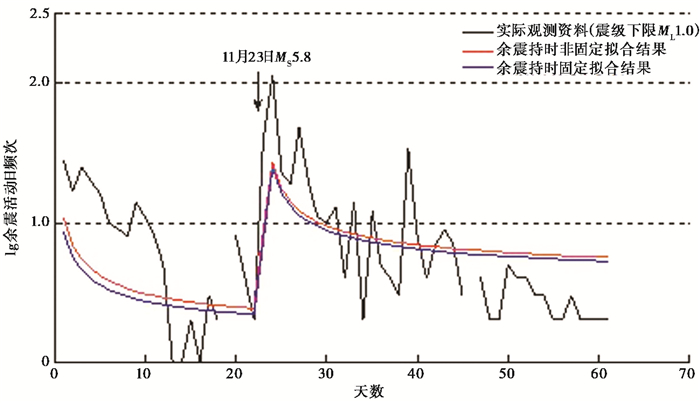
图 5给出2种拟合条件下理论地震活动率和实际地震活动率的对比。由图 5可见，尽管模型评价略有差别，但2者对前郭震群实际资料的拟合差别并不大，均能够较好地反映出实际余震频次的总体衰减特征。另外，实际余震活动的衰减特征更为复杂，具有不规则起伏，而理论计算结果则平滑渐变。由此可知，理论模拟的频次衰减实际上反映了拟合时段下频次衰减的总体特征，若要反映衰减特征随时间的变化，则可能需要更为复杂的模型构建，且模型参数随时间变化而变化。另一方面，从2种方法得到的前郭震区背景地震活动率r值均在约10^-4d^-1km^-2量级分布，说明该地区具有较低的背景地震活动特征，这与实际观测也较为一致。

3.3 余震活动率回溯性预测检验及讨论

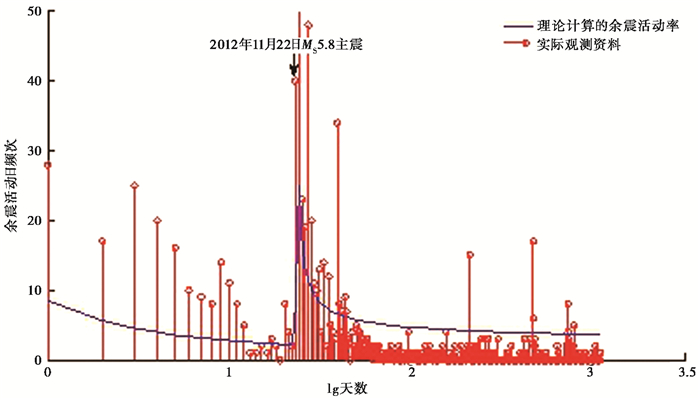
基于上述讨论，利用模型对前郭5.8级震群全部余震活动率随时间的变化进行了回溯性预测检验。由于前郭震群2016年10月24日前后就已基本结束，实际余震持续时间t_a=1089天，因此采用余震持续时间t_a固定的拟合方式确定参数，即Aσ=0.0136MPa、r=1×10^-4d^-1km^-2。图 6为截至2016年10月24日模型计算的理论余震活动率(日频次)变化和实际观测结果的对比。为了更好地显示早期的余震活动变化，取时间轴为对数坐标。可见预测结果与实际资料有较好的正相关，对于2组主震群前后的余震频次起伏有较好的呈现。大约100天后的理论地震频次略高于实际，说明模型计算的余震活动率衰减较慢。在11月23日的最大主震M_S5.8同震期间，理论频次远低于实际。分析其原因，一是同震库伦应力变化在主破裂面附近的负值分布，这些负值区对应于地震活动率相对背景活动率的降低区域，而在主震后早期时段，负的库伦应力带来的“降低”影响最大，随着时间推移，这种影响越来越小；二是介质粘弹性质(Dieterich，1994；Helmstetteret al，2009；蒋海昆等，2012)对应力扰动的滞后影响，事实上，主震同震应力扰动导致的直接余震活动并非余震活动的全部，余震发生还包括余滑、粘弹应力松弛等触发机制(Deng et al，1999；Perfettini et al，2004；曲均浩等，2012)；三是本文仅考虑了5次主震的余震触发，忽略了其他较强余震所导致的高阶余震活动(Ogata，1988；Marsan，2006)。许多强余震能够触发其自身的余震，特别是在震后早期强余震较为丰富阶段，序列实际地震频次包含了大量高阶余震活动，而这一部分在模型中并无体现。另外，2014年以后，虽然也发生了几次4级强余震，但根据实际观测目录显示，相对于5.8级主震同震期间而言，这几次4级余震后续频次的起伏变化并不显著，因此对模型预测结果的影响相对较弱。

4 结论

(1) 基于速率-状态依从地震活动率模型(Dieterich，1994)，以2013年前郭5.8级地震序列为例，探讨了模型参数相关性对实际拟合及预测结果的影响。根据余震持时t_a与Aσ、r的相关性，可分为余震持时固定和非固定2种拟合方式。实际拟合中，如果能依据实际资料确定余震持续时间，则采用余震持时固定的拟合方式可大大提升拟合效率。但当t_a不确定时，同时拟合Aσ和r反而能够获得更大的对数似然函数lnL值，适用于震后早期情况。由此也可以看出，由于模型参数相关性的影响，模型参数拟合存在多种可能的最优结果，对于参数的物理解释需倍加谨慎。

(2) 模拟了前郭5.8震群余震活动率随时间的变化。结果显示理论预测值与实际观测值在变化趋势上吻合较好，特别是前郭震群的前后2组主震对余震活动的连续触发现象，在5.8级地震同震期间，理论余震频次也达到了最高值。2种条件下的拟合结果均显示，前郭地区背景地震活动率为10^-4d^-1km^-2量级，基本符合前郭地区历史地震活动较弱的实际情况，也从侧面证明了模型参数拟合的合理性。存在的问题是，模型以同震库伦应力变化作为初始应力扰动，可能忽略了应力松弛、余滑等实际物理过程以及高阶余震活动的影响，这一假设条件可能导致了主震后早期理论余震频次与实际值之间的较大偏差。

致谢: 本研究使用了中国地震局地球物理研究所提供的震源机制解结果以及吉林省地震局产出的序列目录资料，使用了美国Golden software公司及MathWorks公司发布的一系列绘图及计算软件，谨此致谢。感谢编辑部老师对文章最终修改校稿的详细意见。