中国地震  2019, Vol. 35 Issue (3): 476-487
引用本文
唐明帅, 王海涛, 魏芸芸, 等. 2019. 接收函数分析中强地震前后地壳泊松比变化在新疆地区的初步应用. 中国地震, 35(3): 476-487.   
Tang Mingshuai, Wang Haitao, Wei Yunyun, et al. 2019. Preliminary Application of Crustal Poisson's Ratio Variations of Crustal Media before and after the Moderate-strong Earthquakes in Xinjiang by Using P Receiver Function. Earthquake Research in China, 35(3): 476-487.  
接收函数分析中强地震前后地壳泊松比变化在新疆地区的初步应用
唐明帅1, 王海涛2, 魏芸芸1, 李艳永1, 王琼1, 魏斌1, 苏金波1     
1. 新疆维吾尔自治区地震局, 乌鲁木齐 830011;
2. 中国地震台网中心, 北京 100045
收稿日期：2019-03-05; 修定日期：2019-05-31
项目类别：新疆维吾尔自治区自然科学基金（2016D01A061）、地震科技星火计划项目（XH15046）、国家自然科学基金（41674063、41474051）、新疆维吾尔自治区优秀青年科技人才培养项目、新疆主动震源创新研究团队共同资助
作者简介：唐明帅, 女, 1976年生, 高级工程师, 主要从事地震分析和地震学研究。E-mail:tmings65@sina.cn
通讯作者：王海涛, 通讯作者, 男, 1961年生, 研究员, 主要从事地震监测预报研究。E-mail:ht.wang@263.net
摘要：利用远震P波接收函数，联合接收函数H-κ叠加方法和时间窗滑动方法，分析了新疆31次中强地震前后地壳介质泊松比随时间的变化。结果显示，5次MS6地震中有4次地震、17次5.0≤MS≤5.8地震中有4次地震、9次4.6 ≤ MS ≤ 4.9地震中有1次地震观测到震前泊松比出现低值异常，变化形态特征呈“V”字型（乌苏台呈双“V”字型），地震发生在“V”字型的尾端，地震发生后，泊松比继续回升。根据地壳泊松比的下降幅度、后续变化过程、发震时间以及出现这些变化的地震震级和震中距，认为在新疆地区现有的台网密度下，利用远震P波接收函数可以对重点监视防御区的地下介质泊松比变化进行动态监测。6级以上地震限于震中距100km之内台站，5级以上地震限于震中距50km之内台站，在进行地壳泊松比滑动分析时，需要挑选相关性好、莫霍面一次反射转换波（Ps）清晰且到时一致的接收函数。结合31次震例分析，认为可在新疆东部选择雅满苏（YMS）、中部选择库米什（KMS）、北天山选择乌苏（WSU）、南天山中段选择乌什（WUS）、柯坪块体选择八盘水磨（BPM）、阿尔金断裂尾端选择于田（YUT）地震台用于动态监测附近区域地下介质泊松比变化，尽管喀什-乌恰交汇区地震频发，但由于乌恰（WUQ）台接收函数中莫霍面一次反射转换波Ps震相到时复杂，可能不适用于滑动分析MS5地震前后泊松比变化。
关键词：接收函数    中强地震前后    地壳泊松比变化    新疆地区    
Preliminary Application of Crustal Poisson's Ratio Variations of Crustal Media before and after the Moderate-strong Earthquakes in Xinjiang by Using P Receiver Function
Tang Mingshuai1, Wang Haitao2, Wei Yunyun1, Li Yanyong1, Wang Qiong1, Wei Bin1, Su Jinbo1     
1. Earthquake Agency of Xinjiang Uygur Autonomous Region, Urumqi 830011, China;
2. China Earthquake Networks Center, Beijing 100045, China
Abstract: We analyzed the variations characteristics of Poisson ratio in crustal media before and after the 31 moderate-strong earthquakes in Xinjiang by using P receiver function, stacking method of receiver function and time window sliding method. The results show that there are 4 events in 5 earthquakes with MS6.0 and 5 earthquakes in 5.0 ≤ MS ≤ 5.8 earthquakes have observed a significant low value anomaly in the Poisson's ratio before the earthquake. The morphological characteristics are of "V" type, and the earthquake occurred at the end of the formation of the"V". After the earthquake, the Poisson ratio continued to rise. According to the crustal Poisson's ratio of the descending process, variations process, seismic time, and the magnitude and epicentral distance of the earthquakes, it is considered that under the existing network density in Xinjiang, the P-wave receiver function can be used to monitor the dynamic change of Poisson's ratio of underground medium in the defense zone. Earthquakes with MS ≥ 6.0 are limited to stations within 100km and with MS ≥ 5.0 are limited to stations within 50km of the epicenter. In the performance of the analysis of crustal Poisson's ratio slip, it is necessary to select the good correlation and Moho surface reflection converted wave (Ps) with clear and consistent receive function. Due to the complex crustal structure in Xinjiang and the different receiving functions of different seismic stations, it is important to select the appropriate tracked stations. Combined with the analysis of 31 earthquake cases in this paper, it is considered that the selection of station are Yamansu(YMS) in the eastern part of Xinjiang, Kumishi(KMS) in the middle of Xinjiang, Wusu(WSU) in the northern Tianshan Mountains, Wushi(WUS) in the middle of the southern Tianshan Mountains, Bapanshuimo(BPM) in the Kalpin block, and Yutian(YUT) in the end of Altun break. It is feasible to choose 5 seismic stations for dynamic monitoring of the Poisson's ratio change of the underground medium in the nearby area. Although earthquake in the Kashgar-Wuqia intersection is frequent, due to the complex phase of the Moho surface reflection wave Ps in the receiving function of the Wuqia station, maybe it is not suitable to conduct slid analysis for the Poisson's ratio variations before and after the earthquake with MS5.0.
Key words: Receiver function     Before and after the Moderate-strong earthquakes     The crustal Poisson ratio variation     The Xinjiang area    
0 引言

新疆地处亚欧大陆腹地，在印度洋板块、亚欧板块和西伯利亚板块的相互推挤作用下，形成了由北到南的三大活动地震带(阿尔泰山地震带、天山地震带和昆仑山地震带)。新疆是中国大陆强震活动水平最高的地区之一，其地震频次高、强度大、分布广。新疆维吾尔自治区地震局不断加强地震预测科学基础研究，并积极尝试将各类新技术、新方法应用于地震预测研究工作中，以期提高地震预测的科学水平。在地震孕育过程中，由于孕震区应力的增加，地下介质将产生微破裂等变化，从而引起介质弹性参数发生变化，地震波通过孕育区时，波速会相应发生变化，这是利用波速比异常预测地震的重要依据(冯德益，1981)。远震体波接收函数方法是20世纪80年代发展起来的一种利用地震波形数据研究地球内部结构的重要方法。Zhu等(2000)提出了利用莫霍面一次反射转换震相Ps及多次反射转换震相(PpPs、PsPs+PpSs)叠加搜索能量最大值来确定地壳厚度(H)和地壳介质平均纵横波波速比(κ)的H-κ方法，该方法是目前利用天然地震获得地壳厚度和地壳介质波速比最有效的方法。泊松比表示介质受力后横向与纵向应变之比，是反映地壳介质性质的参数；波速比是介质泊松比的函数，随泊松比的增大而增大(李善邦，1981)。

20世纪50~70年代，日本、前苏联、美国地震科学工作者纷纷注意到了部分中强地震前后的波速异常变化(冯德益，1981)。自20世纪70年代，国内学者应用和达法陆续开展了对中强地震前后波速比异常特征的研究工作(冯德益等，1974；冯锐等，1976；王桂岭等，1979；张学民等，2004；黎明晓等，2004；刁桂苓等，2005；王林瑛等，2008、2011；龙海英等，2011a、2011b；钱晓东等，2013；高朝军等，2013；李艳娥等，2014；张琳琳等，2016)。远震P波接收函数是用远震P波波形的垂直分量对径向分量或切向分量作反褶积后得到的时间序列，由于其在很大程度上消除了震源时间函数和传播路径的影响，可以近似地认为代表了台站下方壳幔结构的响应，其主要由直达波、台站下方速度界面产生的一次反射转换波及多次反射转换波震相组成。与和达法相比，接收函数H-κ叠加方法受地壳介质非均匀性造成的不确定性大大降低，输入数据不受时间服务和震源深度的影响，且能获得整个地壳深度的介质波速比(泊松比)，弥补了使用和达法探测孕震区深部介质波速比变化的不足。

我们联合接收函数H-κ方法和时间窗滑动方法，探索分析2012年6月30日新疆新源-和静MS6.6地震震中距200km内11个固定地震台2009年1月~2012年12月(石场台2006年1月~2012年12月)的地壳介质泊松比变化特征，5个震中距小于130km台站的地壳介质泊松比相继出现了较为明显且持续的下降过程，认为利用远震P波接收函数可以对中强地震前后地下介质泊松比变化进行动态监测(唐明帅等，待刊)。“十五”期间建成的新疆数字测震台网，其台站密度和布局相比以前有较大改善，为本文提供了良好的数据支撑。基于上述背景，本文联合接收函数H-κ方法和时间窗滑动方法，滑动分析了新疆5次6级地震震中距200km范围内、26次4.5~5.9级地震震中距100km范围内的地震台站下方地壳介质泊松比在地震前后随时间的变化。对地震前后出现泊松比异常的震例，分析了地壳介质泊松比下降的时间、幅度和形态。

1 接收函数H-κ叠加搜索方法

对于一维水平单层地壳模型，当给定地壳内介质中P波和S波的平均速度vP和vS，便可以求得地壳的厚度

$ H = \frac{{{t_{{\rm{Ps}}}}}}{{\sqrt {1/\left({v_{\rm{S}}^2 - {p^2}} \right)} - \sqrt {1/\left({v_{\rm{P}}^2 - {p^2}} \right)} }} $ (1)

其中，tPs表示接收函数中莫霍面一次反射转换波Ps震相相对于初至P波的到时差；p为入射P波的射线参数。但是，利用式(1)计算莫霍面的深度需要解决莫霍面深度与波速比之间存在折衷的问题。联合利用莫霍面多次反射转换波震相(PpPs、PsPs+PpSs)与初至P波的到时差可以有效地获得台站下方的地壳厚度H和纵横波速比κ。Zhu等(2000)提出利用莫霍面一次反射转换波Ps及多次反射转换波(PpPs、PsPs+PpSs)叠加搜索能量最大值的方法确定地壳厚度H和纵横波速比κ

$ \begin{array}{*{20}{l}} {{t_{{\rm{Ps}}}} = H[\sqrt {1/\left({v_S^2 - {p^2}} \right)} - \sqrt {1/\left({v_{\rm{P}}^2 - {p^2}} \right)} ]}\\ {{t_{{\rm{P}}{{\rm{p}}{\rm{Ps}}}}} = H[\sqrt {1/\left({v_S^2 - {p^2}} \right)} + \sqrt {1/\left({v_{\rm{P}}^2 - {p^2}} \right)} ]}\\ {{t_{{\rm{PpSs}} + {\rm{PsPs}}}} = H[2\sqrt {1/\left({v_S^2 - {p^2}} \right)} ]}\\ {s(H, \kappa) = \frac{1}{N} \times \sum\limits_{n = 1}^N {{\omega _1}} r\left({{t_1}} \right) + {\omega _2}r\left({{t_2}} \right) - {\omega _3}r\left({{t_3}} \right)} \end{array} $ (2)

其中，r(t)为径向接收函数的振幅；t1、t2和t3表示Ps、PpPs和PsPs+PpSs震相在预测的地壳厚度H和纵横波速比κ条件下对应的到时；ωi(i=1，2，3)为Ps，PpPs和PsPs+PpSs震相的权重系数，且有Σωi=1。利用网格搜索方法可以确定函数s(H，κ)的最大值以及相应的地壳厚度H和地壳介质波速比κ，通过公式σ=0.5(κ2-2)/(κ2-1)可获得相应的地壳介质泊松比σ(李善邦，1981)。应用H-κ方法计算地壳波速比时，百分之几的初始速度模型误差几乎不影响κ值(Zhu et al，2000；危自根等，2011)。

基于接收函数H-κ叠加搜索方法，我们编写了波速(泊松)比随时间变化滑动分析的程序。实现波速(泊松)比随时间变化滑动分析的具体处理过程及思路为：①选择要分析的地震台站；②读取该台挑选好的接收函数；③设置滑动分析开始和结束时间(年-月-日)、滑动窗长和步长(天)；④根据③的设置，确定滑动次数、每次滑动分析的起始时间、包含的接收函数个数；⑤设置接收函数H-κ叠加搜索参数(初始速度、接收函数反射转换波(Ps、PpPs、PsPs+PpSs)权重、地壳厚度及波速比的搜索范围和滑动步长)；⑥计算每个滑动时间段的地壳厚度、波速(泊松)比±误差；⑦画出泊松比随时间的变化图；⑧输出滑动分析计算结果。

2 研究地震和资料选取 2.1 研究震例和台站分布

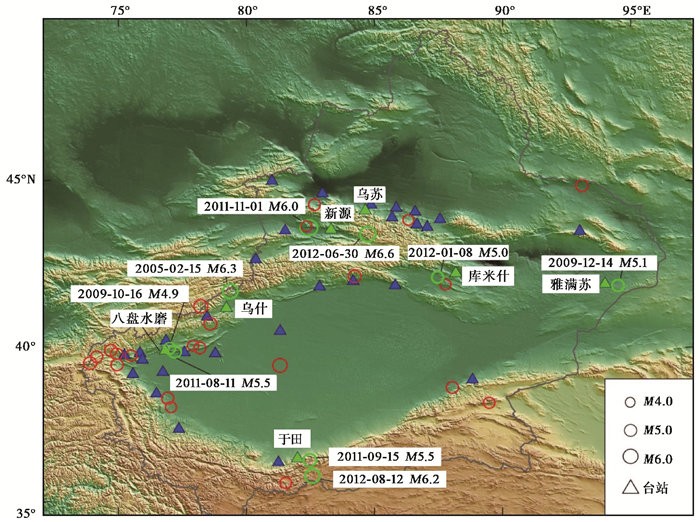
图 1为本文分析的31次中强地震的震中和滑动分析的地震台站分布。31次地震的震级分布为：6.0≤MS≤6.9 5次、5.0≤MS≤5.8 17次、4.6≤MS≤4.9 9次，表 1给出了每次地震的具体信息。对于MS＜6.0的地震，滑动分析震中距100km范围内的地震台站泊松比变化情况；对于MS≥6.0的地震，滑动分析震中距200km范围内的地震台站泊松比变化情况。

图 1 31次中强地震的震中分布和滑动的地震台站分布 绿色圆圈为地震前后出现异常的地震震中；绿色三角为地震前后地壳泊松比出现异常变化的地震台站

表 1 31次中强地震信息
2.2 资料选取及数据处理

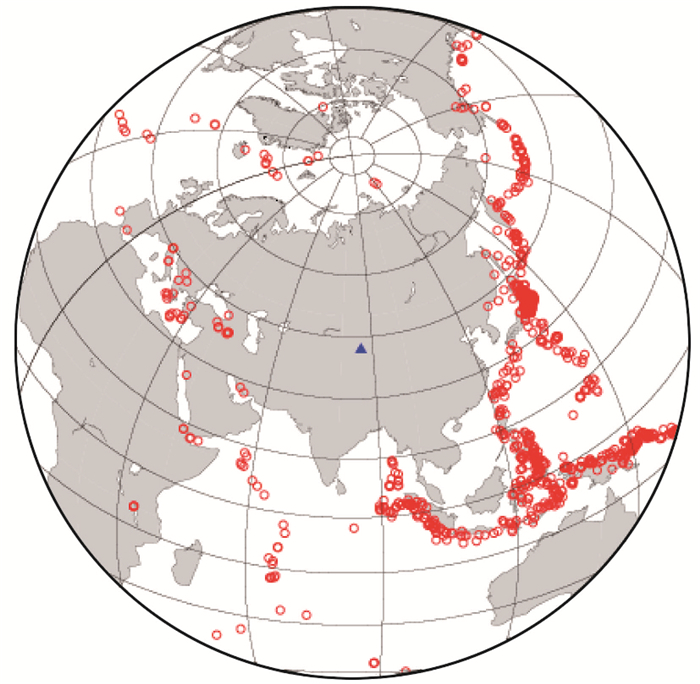
本文收集了36个固定数字地震台自台站建成至2012年12月记录的震中距介于30°~90°、震级M≥5.5的高质量远震波形数据，用于计算接收函数。图 2给出了计算新源台接收函数的远震震中分布。对收集到的远震波形数据进行预处理，应用时间域的迭代反褶积方法提取各台站的接收函数(Ligorría et al，1999)。从时域迭代拟合率≥90%的接收函数中筛选出相关性好、莫霍面一次反射转换波(Ps)清晰且到时一致的接收函数用于泊松比滑动计算。通过整理和归纳已有的关于研究区地壳结构的研究成果，确定vP为6.2km/s，为应用接收函数H-κ叠加方法滑动计算台站下方的地壳介质泊松比提供P波速度值。在滑动分析过程中，为了避免多个极值、H与κ折衷的影响，本文给定的地壳厚度范围为台站下方平均地壳厚度± 0.5km。

图 2 提取接收函数的地震震中分布 红色圆圈为地震分布；蓝色三角为新源台位置
3 地震前后地壳介质泊松比变化特征

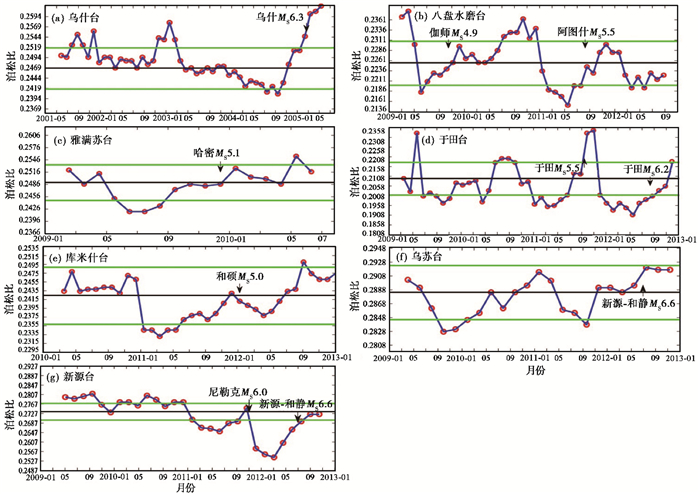
分析表 1中31次地震前后对应台站的地壳泊松比随时间的变化，结果显示，5次MS≥6.0地震中有4次地震观测到震前泊松比变小，26次4.6≤MS≤5.8地震中有5次地震观测到震前泊松比变小。针对震前地壳泊松比出现低值异常的9次地震，表 2给出了泊松比异常地震台站的相关信息，这些地震和台站的具体分布如图 1中的绿色圆圈和绿色三角，图 3为这些台站的地壳泊松比随时间的变化情况，纵坐标的取值范围不一致，主要是由于不同地震台站下方地壳平均泊松比值不同(表 2)。图 3(g)为新源台的地壳泊松比随时间的变化，该台距2012年新源MS6.6地震震中117km。

表 2 地震台站相关信息和泊松比变化信息

图 3 9次中强地震前地壳泊松比异常对应台站的泊松比变化 红色圆圈表示1个窗长对应的泊松比值，对应的时间为该滑动窗长的中间值；黑色直线表示台站下方地壳泊松比均值；绿色直线表示台站平均泊松比计算误差

震前地壳泊松比出现下降的台站，其下降过程较为明显且持续时间相对较长，地壳泊松比变化呈“V”字型，地震发生在“V”字型的回升尾端，地震发生后泊松比继续回升。这些台站的泊松比整体变化形状与祁连5.3级、门源6.4级地震前主动源观测到的震相走时变化形状(呈“V”或双“V”字型)相似(张元生等，2017)。但不同台站之间的泊松比下降幅度和低值持续时间存在差异，这些差异可能与台站观测环境、地下介质性质、地震大小以及震源距不同有关。

4 分析与讨论 4.1 方位变化对泊松比计算结果的影响

在初次滑动计算于田台泊松比时，只挑选时域迭代拟合率≥90%且Ps震相清晰的接收函数做滑动，未对接收函数Ps震相到时一致性做约束(图 4(a))，图 4(b)为这些接收函数的方位分布，图 4(c)为对应接收函数的H-κ叠加图，图 4(d)为泊松比随时间的变化，该台地壳泊松比在2011年于田MS5.5、2012年于田MS6.2地震前未出现持续下降和震后回升的过程。通过人机结合筛选出于田台相关性好、莫霍面一次反射转换波Ps震相清晰且到时一致的接收函数(图 4(e))用作泊松比滑动计算，图 4(f)为对应的方位分布，图 4(g)为对应的H-κ叠加图，图 4(h)为泊松比随时间的变化，地壳泊松比在于田2次地震前均出现不同程度的下降和震后回升过程(图 4(h))。图 4(d)和图 4(h)对应的滑动窗长和步长相同，对比2次滑动计算泊松比所用接收函数的反方位角，泊松比出现异常的接收函数的反方位角集中在80°~120°(图 4(f))，未出现异常的接收函数的反方位角分布较广(图 4(b))。针对接收函数随方位变化的台站，进行地壳泊松比滑动分析时，需要挑选相关性好、莫霍面一次反射转换波(Ps)清晰且到时一致的接收函数。

图 4 于田台接收函数剖面图(a)和(e)、方位分布(b)和(f)、H-κ叠加(c)和(g)与地壳泊松比变化图(d)和(h)
4.2 泊松比计算结果的合理性分析

由于影响泊松比计算精度的主要因素有接收函数波形的相似度、信噪比、方位差异、震中距范围、接收函数个数等，在滑动分析不同台站地壳泊松比之前，先挑选出时域迭代拟合率≥90%的接收函数，再通过人机结合，分析每个台站接收函数的特征，筛选出相关性好、莫霍面一次反射转换波Ps震相清晰且到时一致的接收函数用作泊松比滑动计算。在接收函数满足上述条件后，以2012年新源-和静MS6.6地震为例，另文分析了接收函数个数、后方位角和震中距分布范围对泊松比滑动计算精度的影响，认为这3个因素对计算结果的影响小于图 3观测到的泊松比变化。

接收函数中的莫霍面Ps震相为远震P波近垂直入射到台站下方莫霍面产生的一次反射转换波，由于地壳厚度不变，如果孕震区的波速发生变化，则在强震发生前后不同时间段的接收函数中莫霍面Ps震相到时(tPs)会出现变化。邵学钟等(2013)分析了应用远震Ps转换波随时间变化研究地壳介质动态变化的可行性。在《2012年新源-和静MS6.6地震前后地壳介质泊松比变化》一文中(唐明帅等，待刊)，默认接收函数波形中直达P波对应的时刻为0时刻，我们分析了地震前后地壳泊松比出现异常的乌苏、石场和新源3个台站准重复接收函数的莫霍面Ps转换波到时(tPs)变化，得到震前变小(Ps转换波在地壳内的走时变小)、震后变大(Ps转换波在地壳内的走时变大)的结果，这与观测到的震前泊松比持续降低的结果一致。“震源硬化模型”指出，在失稳源区，岩石在受力过程中存在“硬化”现象，硬化过程中其介质的刚度会增加(陈立德等，2003)，而刚度增加可能导致速度增加，从而使走时缩短。观测结果与利用主动源观测到祁连5.3级、门源6.4级地震前穿过孕震区的地震波走时变小的结论一致(张元生等，2017)。

表 2给出了各台站所用接收函数的数量、通过H-κ叠加所有接收函数得到的各台站的地壳平均泊松比和计算误差，考虑到图 3中各台站泊松比出现明显且持续的低值，表 2也给出各台站的地壳平均泊松比和负向计算误差。泊松比出现明显降低台站的泊松比负向计算误差在0.004~0.015之间，以平均值为参考，本文观测到的泊松比下降幅度均大于负向计算误差(表 2)。由于接收函数反映的是台站下方及周围较小距离的三维空间的介质结构，故不能排除由于莫霍面小尺度起伏、介质各向异性和非均匀体散射等造成的影响。本文未对计算结果做滑动平均处理，这些可能是图 3中泊松比在下降或上升过程中出现个别突跳的原因。Audet(2010)分析了PKD台站接收函数功率谱密度(PSD)随时间的变化，发现在2003年圣西米恩M6.5地震后，该台接收函数功率谱密度下降了5分贝(PKD台震中距为65km)，相当于泊松比降低0.02，本文的泊松比降低幅度在0.006~0.02之间。

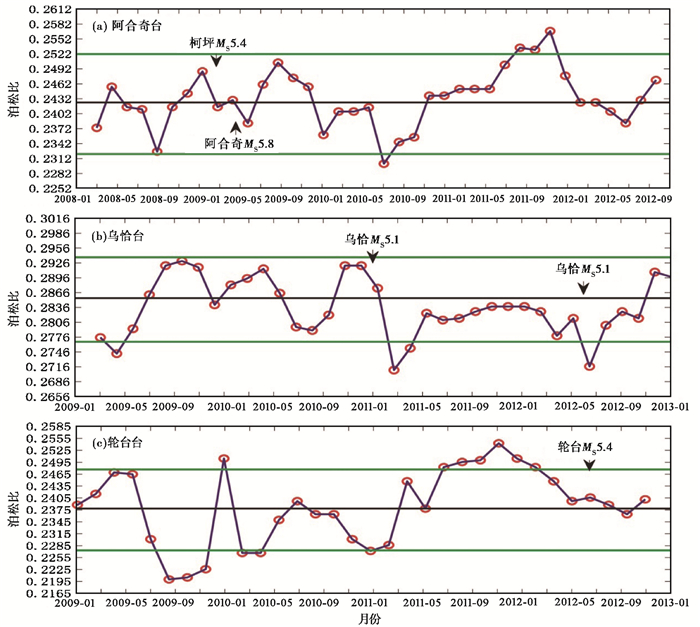
观察地壳泊松比在地震前后出现明显变化的9次地震震级和震中距(表 1中加“*”的地震，图 1中的绿色圆圈)，我们注意到表 1中序号2、3、10、23和24对应的5次5级地震(2009年柯坪MS5.4地震、2009年阿合奇MS5.8地震、2011年乌恰MS5.1地震、2012年乌恰MS5.1地震和2012年轮台MS5.4地震)在震中距介于15~41km的台站(阿合奇(AHQ)、乌恰(WUQ)和轮台(LTA)台)，其地壳泊松比在地震前后没有出现明显的变化(图 5)。通过分析3个台站的接收函数波形特征，发现阿合奇(AHQ)台接收函数中莫霍面的反射波震相Ps能量比较弱且到时不一致，乌恰(WUQ)和轮台(LTA)台的莫霍面反射波Ps震相能量较强但形状复杂、到时变化较多，这些因素可能是导致未观测到地壳泊松比在地震前后出现变化的原因。表 1中序号11对应的MS5.5地震前后八盘水磨(BPM)台(震中距31km)的地壳介质泊松比出现较为明显且持续的下降过程(图 3(b))，在该地震东部震中距为32km的西克尔(XKR)台未观测到该现象(图 1)。

图 5 5次5级震中距15~41km地震震前无明显下降的地壳泊松比变化图(图注同图 3)
5 结论

通过分析新疆31次中强地震前后地壳介质泊松比随时间的变化，5次MS6地震中有4次地震、26次4.6≤MS≤5.8地震中有5次地震观测到震前泊松比出现低值异常，变化形态特征呈“V”字型，地震发生在“V”字型的尾端，地震发生后，泊松比继续回升。根据地壳泊松比的下降幅度、后续变化过程、发震时间以及出现这些变化的地震震级和震中距，认为在新疆目前的台网密度下，利用远震P波接收函数可以对重点监视防御区地下介质泊松比变化进行动态监测。6级以上地震限于震中距100km之内的台站，5级以上地震限于震中距50km之内的台站。由于新疆地区地壳结构复杂，不同地震台站的接收函数特征不同，因此被跟踪台站的选择十分重要，位于新疆东部的雅满苏(YMS)和新疆中部的库米什(KMS)地震台站接收函数波形比较清晰、莫霍面一次反射转换波Ps震相清晰且到时一致，可用于动态监测台站附近区域地下介质泊松比变化，北天山可选择乌苏(WSU)台、南天山中段可选择乌什(WUS)台、柯坪块体可选择八盘水磨(BPM)台、阿尔金断裂尾端可选择于田(YUT)台用于动态监测地下介质泊松比变化。尽管喀什-乌恰交汇区地震频发，由于乌恰(WUQ)台接收函数中莫霍面Ps震相复杂且到时丰富，不宜用于滑动分析MS5地震前后地壳泊松比变化。

致谢: 感谢审稿专家提出的宝贵意见和建议。
参考文献
陈立德、付虹, 2003, 地震预报基础与实践, 北京: 地震出版社.
刁桂苓、周仕勇、刘杰等, 2005, 岫岩地震序列的平均波速比前兆异常, 华北地震科学, 23(4): 1-5. DOI:10.3969/j.issn.1003-1375.2005.04.001
冯德益, 1981, 地震波速异常, 北京: 地震出版社.
冯德益、谭爱娜、王克芬, 1974, 近地震波速异常与地震预报, 地球物理学报, 17(2): 84-98.
冯锐、庞庆衍、傅征祥等, 1976, 海城地震前后地震波速比的变化, 地球物理学报, 19(4): 295-305.
高朝军、宋春燕、张琳琳等, 2013, 新疆新源、和静交界6.6级地震前后波速比异常特征研究, 内陆地震, 27(2): 121-126. DOI:10.3969/j.issn.1001-8956.2013.02.003
黎明晓、张晓东, 2004, 应用多台法测定华北地区地壳的平均波速比, 地震, 24(1): 163-169. DOI:10.3969/j.issn.1000-3274.2004.01.024
李善邦, 1981, 中国地震, 北京: 地震出版社.
李艳娥、王林瑛、郑需要, 2014, 汶川地震前后波速比变化特征的再研究, 地震学报, 36(3): 425-432. DOI:10.3969/j.issn.0253-3782.2014.03.008
龙海英、聂晓红、唐兰兰, 2011a, 新疆和静5.6级地震前波速比异常震例分析, 中国地震, 27(2): 147-154.
龙海英、聂晓红、唐兰兰, 2011b, 新疆乌苏5.1级地震前波速比异常震例研究, 地震研究, 34(2): 126-130.
钱晓东、苏有锦, 2013, 2008年攀枝花6.1级地震前后波速比变化研究, 地震研究, 36(1): 15-23. DOI:10.3969/j.issn.1000-0666.2013.01.003
邵学钟、张家茹、范会吉, 2013, 地震转换波测深, 北京: 地震出版社.
唐明帅、王海涛、魏芸芸等, 2019, 2012年新源-和静MS6.6地震前后地壳介质泊松比变化, 地震地质, 待刊.
王桂岭、吴秀莲、敖雪明, 1979, 新疆一些中强震前后的波速比异常, 西北地震学报, 1(2): 1-8.
王林瑛、郭永霞、刘芳等, 2008, 文安地震前后首都圈分区波速比时变特征, 地震学报, 30(3): 240-253. DOI:10.3321/j.issn:0253-3782.2008.03.003
王林瑛、李艳娥、李芳等, 2011, 汶川地震前后地震波速比和视速度变化特征的研究, 地震学报, 33(1): 1-14. DOI:10.3969/j.issn.0253-3782.2011.01.001
危自根、陈凌、杨小林, 2011, 辽东台隆、燕山带和兴蒙造山带台站下方地壳厚度和平均波速比(vP/vS)的横向变化及其构造意义, 地球物理学报, 54(11): 2799-2808. DOI:10.3969/j.issn.0001-5733.2011.11.010
张琳琳、高朝军, 2016, 新疆天山地区的波速比异常分析, 中国地震, 32(1): 118-126. DOI:10.3969/j.issn.1001-4683.2016.01.011
张学民、刁桂苓、束沛镒等, 2004, 华北地区地下介质波速比值(vP/vS)研究, 地震地质, 26(2): 305-317. DOI:10.3969/j.issn.0253-4967.2004.02.012
张元生、王宝善、陈颙等, 2017, 两次强震发生前后主动源观测走时数据的变化, 地球物理学报, 60(10): 3818-3822.
Audet P, 2010, Temporal variations in crustal scattering structure near Parkfield, California, using receiver functions, Bull Seism Soc Am, 100(3): 1356-1362.
Ligorría J P, Ammon C J, 1999, Iterative deconvolution and receiver-function estimation, Bull Seism Soc Am, 89(5): 1395-1400.
Zhu L P, Kanamori H, 2000, Moho depth variation in Southern California from teleseismic receiver functions, J Geophys Res, 105(B2): 2969-2980. DOI:10.1029/1999JB900322