中国地震  2019, Vol. 35 Issue (3): 531-540
引用本文
杨晶琼, 杨周胜, 许亚吉, 等. 2019. 云南地震台网震级对比研究. 中国地震, 35(3): 531-540.   
Yang Jingqiong, Yang Zhousheng, Xu Yaji, et al. 2019. Comparative Study on the Magnitude of Yunnan Digital Seismic Network. Earthquake Research in China, 35(3): 531-540.  
云南地震台网震级对比研究
杨晶琼, 杨周胜, 许亚吉, 秦敏, 张会苑, 蔡明军, 李姣     
云南省地震局, 昆明 650224
收稿日期：2019-04-30; 修定日期：2019-07-25
项目类别：中国地震局地震科技星火计划项目（XH18043）资助
作者简介：杨晶琼, 女, 1968年生, 高级工程师, 主要从事地震编目分析与数字地震资料应用研究。E-mail:yjq6@163.com
通讯作者：杨周胜, 通讯作者, 男, 1967年生, 副研究员, 主要从事地震监测研究。E-mail:yeayzs@sohu.com
摘要：利用云南地震台网记录的云南及其周边地区2000~2017年的宽频带数字地震资料，按照新的震级国家标准《地震震级的规定》（GB17740- 2017）的测定方法，使用同一套软件，对地方性震级ML、面波震级MS、宽频带面波震级MS（BB）、短周期体波震级mb、宽频带体波震级mB（BB）和矩震级MW重新进行人工测量。并分别用一般线性回归和正交回归方法，对不同震级之间的关系进行对比，给出它们之间的经验关系式。研究结果表明：①当M < 4.5时，各种震级之间相差不大，使用地方性震级ML可以较好地表示地震的大小，也能够更加充分地反映区域特性；当4.5≤M < 8.0时，宽频带面波震级MS（BB）和矩震级MW均能较好地表示地震的大小，但矩震级MW的测定需要一定时间，因此在速报工作和大震应急中，可以使用MS（BB）表示地震的大小；MS（BB）的测定方法与国际接轨，消除0.2的震级偏差。②对于面波震级MS和宽频带面波震级MS（BB），由于面波测量的位置、计算公式和量归函数不同，MS比MS（BB）系统偏高0.2左右；短周期体波震级mb较宽频带体波震级mB（BB）整体偏小0.2左右，主要区别在于仿真模式。③宽频带面波震级MS（BB）和宽频带体波震级mB（BB）均在垂直向原始宽频带记录上直接测定，取消波形仿真环节，另外，相比测定mB（BB）震中距要求大于5度，许多台站被限制，MS（BB）更利于区域台网测定。④当3.5≤ML≤6.5时，ML较MW整体偏大；MS≥3.5时，MS也较MW整体偏大，且均随着震级增加，偏差值呈上升趋势。⑤当M≥8.0时，面波震级出现饱和现象，使用矩震级MW表示M≥8.0地震的大小。
关键词：震级国家标准    地方性震级    面波震级    体波震级    矩震级    
Comparative Study on the Magnitude of Yunnan Digital Seismic Network
Yang Jingqiong, Yang Zhousheng, Xu Yaji, Qin Min, Zhang Huiyuan, Cai Mingjun, Li Jiao     
Yunnan Earthquake Agency, Kunming 650224, China
Abstract: Using the broadband digital seismic data recorded by the Yunnan Digital Seismic Network in Yunnan and its surrounding areas during 2000~2017, according to the determination method of the New National Standard "Earthquake Magnitude Regulation" (GB17740- 2017), the same set of software should be used to re-measure manually the local magnitude ML, the surface wave magnitude MS, the wide band surface wave magnitude MS(BB), the short period body wave magnitude mb, the wide band wave magnitude mB(BB) and the moment magnitude MW. The relationship between different magnitude is compared with the general linear regression and orthogonal regression methods respectively, and the empirical relations between them are given. The results show that there is little difference between the various magnitude:① When M < 4.5, and the size of the earthquake can be better represented by the local magnitude ML, and can reflect the regional characteristics more fully. When 4.5 ≤ M < 8.0, the wide band surface wave magnitude MS(BB) and the moment magnitude MW can better represent the magnitude of the earthquake. However, the determination of moment magnitude MW takes a certain amount of time. So in the rapid reporting work and earthquake emergency response, MS(BB) can be used to indicate the size of the earthquake. MS(BB) determination method and international standards, eliminate 0.2 of the magnitude deviation. ② For surface wave magnitude MS and wide band surface wave magnitude MS(BB), the calculation formula and the regression function are different. The MS ratio MS(BB) system is about 0.2 higher. The short period body wave magnitude mb is smaller than the wide band Body wave magnitude mB(BB), and the overall is about 0.2. The main difference should be in the simulation mode. ③ Wide band surface wave magnitude MS(BB) and wide band wave magnitude mB(BB) are directly measured vertically to the original wide band record, eliminating the waveform simulation link. In addition, compared to the determination of mB(BB) epicenter distance requirements greater than 5 degrees, many stations will be limited. MS(BB) is more conducive to regional network measurement. ④ When 3.5 ≤ ML ≤ 6.5, ML is larger than MW as a whole. When MS ≥ 3.5, MS, MW is also the overall size, and with the increase of the magnitude, the deviation value is on the rise. ⑤When M ≥ 8.0, the surface wave magnitude appears saturated, with the moment magnitude MW to indicate the size of the earthquake with M ≥ 8.0.
Key words: National standard of magnitude     Local magnitude     Surface wave magnitude     Body wave magnitude     Moment magnitude    
0 引言

震级是对地震大小的相对度量，在地震预报和其他有关地震的研究中是一个重要的参数(陈运泰等，2000、2004)。1935年，Richter(1935)在研究美国南加州的地震时引入了第一个震级标度——地方性震级ML，为震级的发展奠定了基础，使地震定量研究得到不断发展。1945年，Gutenberg(1945)将测定地方性震级ML的方法推广到远震，提出了面波震级标度和体波震级标度。为了克服大地震的震级饱和问题，Kanamori(1977)、Purcaru等(1978)、Hanks等(1979)几乎同时提出了矩震级标度MW。

2000年以后，世界各国地震台站逐步完成了数字化改造，数字地震观测系统得到广泛应用，国际地震学与地球内部物理学联合会(IASPEI)制定了新的震级标准，矩震级测定纳入国际地震中心、美国地质调查局国家地震信息中心等国际地震监测机构的日常工作中。中国地震局于2012年成立工作组，开展对国家标准《地震震级的规定》(GB 17740—1999)的修定工作，新的震级国家标准《地震震级的规定》(GB 17740—2017)(以下简称新国标)于2017年5月12日正式发布(刘瑞丰等，2017)。

使用不同的震级标度测定同一地震，通常会得到多个不同的震级，而不同震级标度测定值之间的关系一直备受地震学界的关注(刘瑞丰等，2005、2011；Bormann et al，2007；任克新等，2008；唐淋等，2018)。考虑到不同震级测量的方法不同，所使用的仪器也不同，因此在地震台网的震级测定中，不同的震级之间一律不进行换算，但是在地震活动性分析，特别是在地震预测研究中，通常使用经验公式将不同的震级换算成统一的一种震级(刘瑞丰等，2006；杨晶琼等，2013b)，新的震级国家标准实施后，科研人员急需了解各种震级如何测定，震级之间又有怎样的经验关系，基于此，本文按新震级国家标准规定的测定方法，使用同一套软件，重新测定了云南台网各类震级，并进行回归计算，给出不同的关系式。

1 震级及其测定

新国标规定了地方性震级ML、短周期体波震级mb、宽频带体波震级mB(BB)、面波震级MS、宽频带面波震级MS(BB)和矩震级MW的测定方法，其中，ML、mb和MS是相对于固定地震波周期的震级，而MS(BB)和mB(BB)是宽频带震级，所使用面波周期为3s < T < 60s，体波周期为0.2s < T < 30.0s(刘瑞丰等，2018)。

地方性震级是选用震中距为1000km以内地震波(S波或Lg波)记录测定的震级，用ML表示。面波震级是选用地震面波记录测定的震级，通常用水平向面波记录测定，用MS表示；选用垂直向宽频带面波记录测定的面波震级称为宽频带面波震级，用MS(BB)表示。体波震级是选用地震体波记录测定的震级，其中选用短周期体波记录测定的体波震级称为短周期体波震级，用mb表示；选用宽频带体波记录测定的体波震级称为宽频带体波震级，用mB(BB)表示。矩震级是用地震矩换算的震级，用MW表示。各种震级具体的测定方法，见表 1。

表 1 各种震级的测定

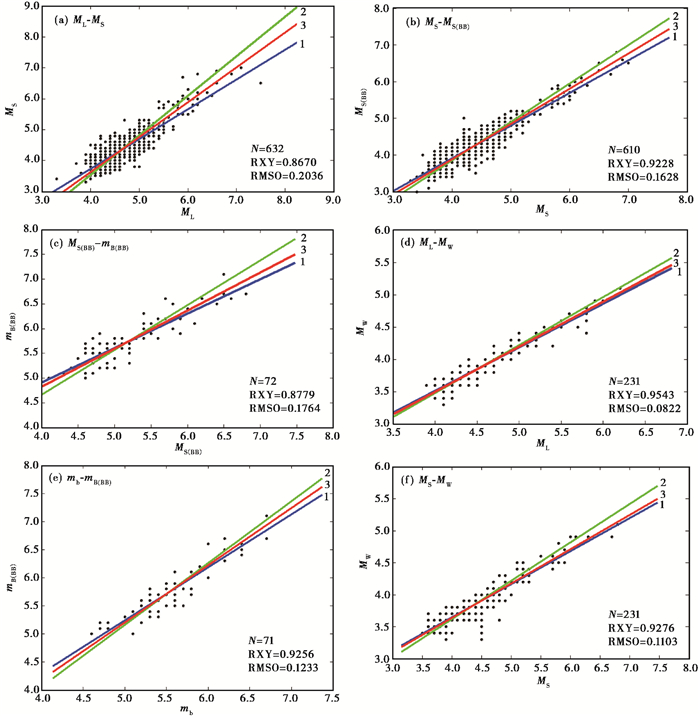
直线1为SR1线性回归结果；直线2为SR2线性回归结果；直线3为OR正交回归结果；N为地震数；RXY为正交回归的相关系数；RMSO为正交回归的均方根

2 不同震级之间的对比

按照新国标规定的测定方法，对于4.0级以上地震，同时测定ML、MS和MS(BB)；对于5.0级以上的地震，除此之外，还要测定mb和mB(BB)；对2008年以来ML≥3.0的地震波形数据，反演震源波谱参数，计算地震矩Mo，得到矩震级MW，并分别对不同震级之间的关系进行回归分析与对比，得到的回归关系式如表 2所示，相应的回归直线如图 1所示，图 2~7为不同震级之间实际测量结果的差值分布图，表 3~8为用正交回归方法(OR)(刘瑞丰等，2007)得到的不同震级之间的关系对照表。

表 2 不同震级之间的关系

图 1 不同震级之间的关系 注:表中SR1和SR2表示一般线性回归, OR表示正交回归。

图 2 ML和MS差值分布

图 3 MS和MS(BB)差值分布

图 4 MS(BB)和mB(BB)差值分布

图 5 ML和MW差值分布

图 6 mb和mB(BB)差值分布

图 7 MS和MW差值分布

表 3 ML与MS对照表

表 4 MS与MS(BB)对照表

表 5 MS(BB)与mB(BB)对照表

表 6 ML与MW对照表

表 7 mb与mB(BB)对照表

表 8 MS与MW对照表
2.1 地方性震级ML与面波震级MS之间的对比

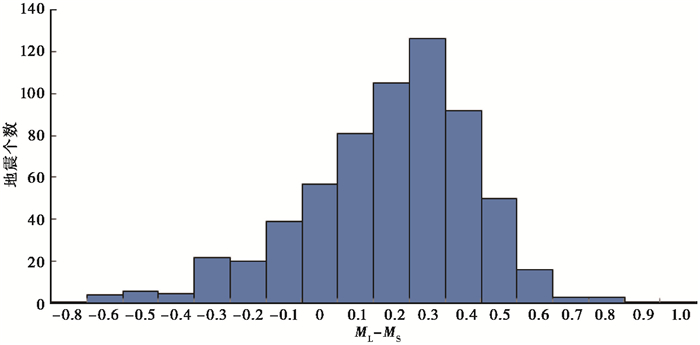
用于回归分析的资料为2000~2017年的632次地震，其震中距的范围为1000km以内，震级范围为3.3≤ML≤7.5，ML与MS差值分布见图 2，由图 2可见，绝大多数地震的ML与MS之间的差值在-0.3~0.5之间，差值为0.3的地震数最多，震级差绝对值最大为1.0，最小为0，平均为0.26，在0.3以内的事件有450个，占总数的71.2%。从图 1可以看出，由正交回归得到的ML与MS的关系即直线3的斜率略大于1，并且在线性回归得到的直线1和2中间，由正交回归方法得到的如下表达式

$ {M_{\rm{S}}} = 1.13{M_{\rm{L}}} - 0.87 $ (1)

这与该区域之前的一些研究结果较相似(杨晶琼等，2013b)，与1971年郭履灿①根据邢台地震资料进行统计得到的关系式

①郭履灿, 1971, 华北地区的地方性震级ML和面波震级MS经验关系(全国地震工作会议资料)。

$ {M_{\rm{S}}} = 1.13{M_{\rm{L}}} - 1.08 $ (2)

之间存在明显系统偏差。

由式(1)得到表 3，从表 3可以看出，对于ML < 4.5地震，ML与MS之间差异偏大，这是因为云南地区ML < 4.5地震的面波不发育，测量中较难完全满足新国标对测定MS在震中距和周期方面的要求。

2.2 面波震级MS与宽频带面波震级MS(BB)之间的对比

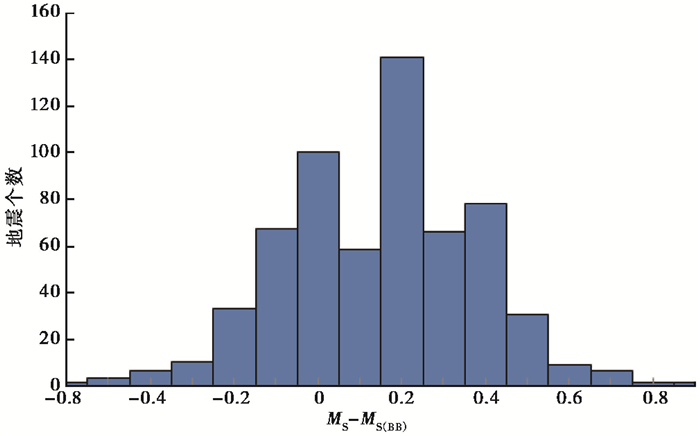
选用资料为2000~2017年的610次地震，其震中距为22 < Δ < 130，震级范围为3.3≤MS≤7.0，由图 1可以看出，由正交回归得到的MS与MS(BB)的关系即直线3的斜率几乎等于1，拟合相关系数高达0.9228，均方根为0.1628，回归的离散性非常小。MS与MS(BB)差值分布见图 3，由图 3可以看出，绝大多数地震的MS与MS(BB)差值在-0.2~0.5之间，差值为0.2的地震数量最多，震级差绝对值最大为0.9，最小为0，平均为0.20。从表 4可以看出，MS与MS(BB)存在一定系统偏差，差值在0.2左右。对于MS < 4.5的地震，MS比MS(BB)偏大0.1；而对于MS≥4.5的地震，MS比MS(BB)偏大0.2。

MS平均偏高的原因可归结为：MS(BB)使用垂直向面波资料测定，而MS使用2个水平向记录，垂直向只包含了独立的瑞利波，而水平向却包含了叠加在一起的瑞利波和勒夫波；另外，两者使用的量规函数不一样，由式(1)、(2)可以看出，两者使用的量规函数相差0.2，这应该是最主要的原因。垂直向只包含具有膨胀成分的瑞利波，瑞利波与震源类型关系不是很密切，用不同震中距、不同方位角的台站记录的瑞利波测定面波震级比较稳定。另外，MS(BB)只在1个方向且是在原始记录上测量，相较MS要快很多。

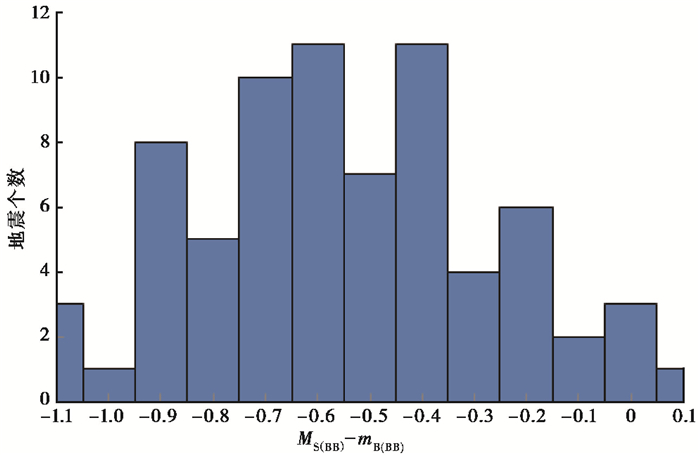
2.3 宽频带面波震级MS(BB)与宽频带体波震级mB(BB)之间的对比

MS(BB)和mB(BB)是IASPEI制定的新的震级标准中的2个震级新标度(Bormann et al，2009)，本文用于回归分析的资料为2000~2017年的72次地震，震级范围为4.1≤MS(BB)≤6.8，MS(BB)与mB(BB)差值分布见图 4，由图 4可以看出，绝大多数地震的MS(BB)与mB(BB)差值在-0.9~-0.2之间。虽然二者都不经过仿真，在垂直向上直接测定，但由于测量波列和方法上存在的差异，对于不同大小的地震，它们是不一样的。从表 5可以看出，对于MS(BB)7.5左右的地震，二者几乎相等，而对于MS(BB) < 7.0的地震，MS(BB)均小于mB(BB)。

2.4 地方性震级ML与矩震级MW之间的对比

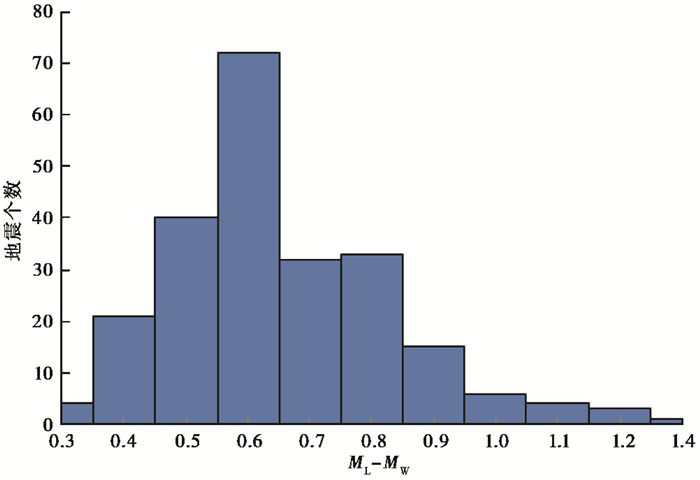
矩震级是一个均匀的震级标度，本文所用数据为2008~2017年的231次地震，震级范围为3.9≤ML≤6.2，图 1显示，拟合相关系数高达0.9543，均方根为0.0822，回归的离散性非常小。表 1中由OR得到的表达式，与该区域之前的研究结果非常相似(杨晶琼等，2013a)。由ML与MW差值分布图(图 5)可以看出，绝大多数地震的ML与MW之间的差值在0.4~0.9之间，差值为0.6的地震数最多，震级差绝对值平均为0.7。从表 6可以看出，ML较MW整体偏大，且偏差值随着震级增加而增大。

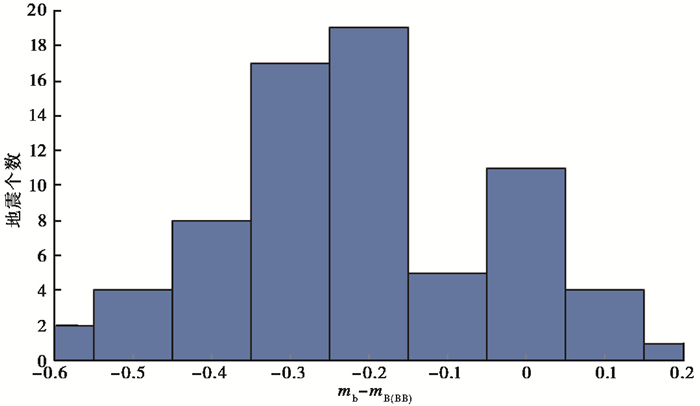
2.5 短周期体波震级mb与宽频带体波震级mB(BB)之间的对比

本文用于回归分析的资料为2000~2017年的71次地震，震级范围为4.6≤mb≤6.7，mb与mB(BB)差值分布见图 6。由图 6可以看出，绝大多数地震的mb与mB(BB)之间差值在-0.4~0之间，差值为-0.2的地震数量最多，震级差绝对值最大为0.6，最小为0。从表 7可以看出，mb较mB(BB)整体偏小0.2左右，主要区别在于测定P波振幅的周期差异以及仿真模式，mB(BB)可测量0.2~30 s的体波，mb仅可测量T < 3s的体波，对于区域台网，震中距多在1000km以内，在测量mB(BB)和mb时，无论仿真与否，P波波列周期基本均在0.2~3s之间，因此周期差异影响相对较小，更多考虑的是仿真模式的差异；mb是将垂直向宽频带记录仿真成DD_1短周期地震仪记录后再测量，而mB(BB)则是在垂直向速度型宽频带记录上直接测量。

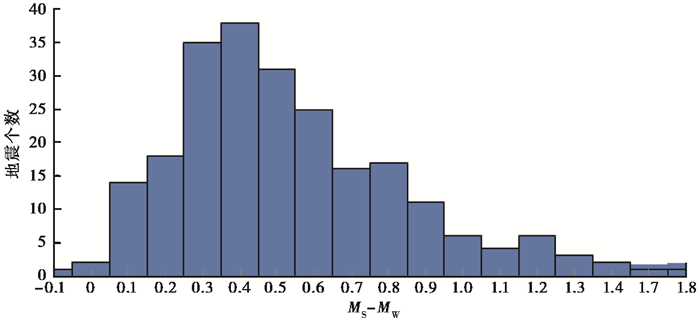
2.6 面波震级MS与矩震级MW之间的对比

选用2008~2017年的231次地震，震级范围为3.5≤MS≤6.8，MS与MW差值分布见图 7。图 7中绝大多数地震的MS与MW之间差值在0.1~0.8之间，差值为0.4的地震数最多，震级差绝对值最大为1.8，最小为0。从表 8可以看出，当MS≥3.5时，MS较MW整体偏大。

3 结论与讨论

按照新的震级国家标准《地震震级的规定》(GB17740—2017)的方法，利用大量实际观测资料对6种震级重新进行人工测量，并对它们之间的关系进行了正交回归分析，得到以下结论：

(1) 当M＜4.5时，各种震级之间相差不大，使用地方性震级ML可以较好地反映区域特性。当4.5≤M＜8.0时，MS(BB)和MW均能较好地表示地震的大小，但MW的测定需要一定时间，因此在地震速报和大震应急中，使用MS(BB)更有优势。

(2) 对于MS和MS(BB)，由于面波测量的位置、计算公式和量归函数不同，MS比MS(BB)系统偏高0.2左右。

(3) 虽然MS(BB)与mB(BB)均是在垂直向上直接测定，但由于测量波列和方法上存在的差异，对于不同大小的地震，二者是不一样的。另外，由于MS(BB)取消波形仿真环节，能较好地提高地震速报和应急处置的时效性，相比mB(BB)震中距要求大于5度，许多台站会被限制，因此，MS(BB)更利于区域台网测定。

(4) 虽然测定mb和mB(BB)使用的P波波列相同，但对区域台网，震中距多在1000km以内，仿真前后P波波列周期也基本均在0.2~3s之间，而mb较mB(BB)整体偏小0.2左右，主要区别在于仿真模式，mb是将垂直向宽频带记录仿真成DD_1短周期地震仪记录后再测量，而mB(BB)则是在垂直向速度型宽频带记录上直接测量。

(5) 当3.5≤ML≤6.5时，ML较MW整体偏大；MS≥3.5时，MS较MW也是整体偏大，且均随着震级增加偏差值呈上升趋势。

(6) 当M≥8.0时，面波震级出现饱和现象，使用矩震级MW表示M≥8.0地震的大小。

致谢: 感谢中国地震局地球物理研究所刘瑞丰研究员对本研究给予的指导和帮助。
参考文献
陈运泰、刘瑞丰, 2004, 地震的震级, 地震地磁观测与研究, 25(6): 1-12. DOI:10.3969/j.issn.1003-3246.2004.06.001
陈运泰、吴忠良、王培德等, 2000, 数字地震学, 1-30, 北京: 地震出版社.
刘瑞丰、陈运泰、Bormann P等, 2005, 中国地震台网与美国地震台网测定震级的对比(Ⅰ)——体波震级, 地震学报, 27(6): 583-587. DOI:10.3321/j.issn:0253-3782.2005.06.001
刘瑞丰、陈运泰、Bormann P等, 2006, 中国地震台网与美国地震台网测定震级的对比(Ⅱ)——面波震级, 地震学报, 28(1): 1-7. DOI:10.3321/j.issn:0253-3782.2006.01.001
刘瑞丰、陈运泰、任枭等, 2007, 中国地震台网震级的对比, 地震学报, 29(5): 467-476. DOI:10.3321/j.issn:0253-3782.2007.05.003
刘瑞丰、任克新、张立文等, 2011, 利用宽频带数字地震资料测定地震震级的方法研究, 地震地磁观测与研究, 32(3): 1-8. DOI:10.3969/j.issn.1003-3246.2011.03.001
刘瑞丰、陈运泰、许绍燮等, 2017, 地震震级的规定(GB 17740-2017), 北京: 中国标准出版社.
刘瑞丰、陈运泰、王丽艳, 2018, 新的震级国家标准的技术要点与主要特点, 地震地磁观测与研究, 39(1): 1-11.
任克新、刘瑞丰、张立文等, 2008, IASPEI新震级标度与传统震级标度的对比, 地震地磁观测与研究, 29(5): 16-21. DOI:10.3969/j.issn.1003-3246.2008.05.003
唐淋、祁国亮、苏金蓉等, 2018, 新国家标准震级标度与传统震级标度对比研究, 地震学报, 40(2): 121-131.
杨晶琼、刘丽芳、杨周胜, 2013a, 云南中小地震矩震级的测定, 地震研究, 36(3): 306-312.
杨晶琼、杨周胜、蔡明军等, 2013b, 云南地区近震震级与面波震级转换关系研究, 中国地震, 29(4): 513-521.
Bormann P, Liu R F, Ren X, et al, 2007, Chinese national network magnitudes their relation to NEIC magnitudes, and recommendations for new IASPEI magnitude standards, Bull Seismol Soc Am, 97(1B): 114-127. DOI:10.1785/0120060078
Bormann P, Liu R, Xu Z, et al, 2009, First application of the New IASPEI teleseismic magnitude standards to data of the China national seismographic network, Bull Seismol Soc Am, 99(3): 1868-1891. DOI:10.1785/0120080010
Gutenberg B, 1945, Amplitudes of surface waves and magnitudes of shallow earthquakes, Bull Seismol Soc Am, 35(1): 3-12.
Hanks T C, Kanamori H, 1979, A moment magnitude scale, J Geophys Res Solid Earth, 84(B5): 2348-2350. DOI:10.1029/JB084iB05p02348
Kanamori H, 1977, The energy release in great earthquakes, J Geophys Res, 82(20): 2981-2987. DOI:10.1029/JB082i020p02981
Purcaru G, Berckhemer H, 1978, A magnitude scale for very large earthquakes, Tectonophysics, 49(3-4): 189-198. DOI:10.1016/0040-1951(78)90177-4
Richter C F, 1935, An instrumental earthquake magnitude scale, Bull Seismol Soc Am, 25(1): 1-32.
云南地震台网震级对比研究
杨晶琼, 杨周胜, 许亚吉, 秦敏, 张会苑, 蔡明军, 李姣