0 引言

河南及邻区(31°~37°N，110°~117°E)位于我国中部略偏东，西部有秦岭东延的豫西山地，包括崤山、熊耳山、伏牛山、外方山，西南有南襄盆地，北部有太行山，南部有桐柏山、大别山，中部和东部为平原，大地构造跨华北板块和扬子板块，地层发育齐全，岩浆活动频繁，地质构造复杂，为内外生成矿作用提供了有利条件，是研究华北、华南乃至中国地壳演化的重要地区(林德超等，1998)。近年来，随着数字地震台站的增加，已经取得了很多关于中国东部地区噪声层析成像的成果。例如，叶庆东等(2014)基于噪声层析成像研究了大别-苏鲁及其邻近地区勒夫波群速度结构，吴萍萍等(2015)研究了大别-苏鲁及其邻区的瑞雷波群速度结构，宫猛等(2017)研究了华北东部壳幔三维S波速度结构等。尽管上述研究部分覆盖本文研究区域，但研究尺度相对较大，且结果讨论关注区域不同，并未针对河南地区地壳速度结构及地质意义进行详细探讨，因此研究该区地壳速度结构，对探讨其速度分布及可能的地质意义具有一定价值。

噪声层析成像作为一种新的成像技术，具有不依赖地震事件、分辨率高等特点。利用该方法可以在地震活动性较弱但地震台站分布较好的地区开展高精度的成像研究。由于噪声层析成像的优越性，近些年该方法在中国大陆及邻区(易桂喜等，2008；Sun et al，2010)、东北地区(Zheng et al，2011；余大新等，2014)、华北地区(唐有彩等，2011；房立华等，2013)、华南地区(Zhou et al，2012；高佳佳等，2017)、天山及周边地区(郭志等，2010)和青藏高原地区(范文渊等，2015；杨志高等，2018)等均得到广泛应用。本文利用河南及周边6个省份39个宽频带和甚宽频带地震台站记录的垂直分量地震背景噪声数据，提取各台站间的经验格林函数，进而将研究区域划分成1°×1°的网格，利用噪声层析成像方法获得了研究区8~25s的瑞利波群速度分布图像。

1 数据来源

收集了河南地震台网及周边河北、山西、陕西、湖北、安徽、山东台网共计39个固定地震台站(图 1)记录的连续波形数据。地震计主要类型为BBVS-60、BBVS-120、CMG-3ESPC和CTS-1，其中多数台站为宽频带(50Hz~60s)地震仪，少数台站为甚宽频带(50Hz~120s)地震仪。从图 1可以看出，除河南东部地区台站分布相对稀疏外，整体分布基本均匀。由于本文提取瑞利波格林函数，因此仅用到瑞利波能量较强的垂直分量的连续波形记录，时间选取范围为2014年1月~2015年12月。

2 数据处理方法

目前，噪声层析成像方法已较为成熟，其数据处理流程由5部分组成：①单台数据预处理；②两两台站长时间波形记录互相关计算与叠加；③频散曲线测量；④质量控制；⑤噪声层析成像。

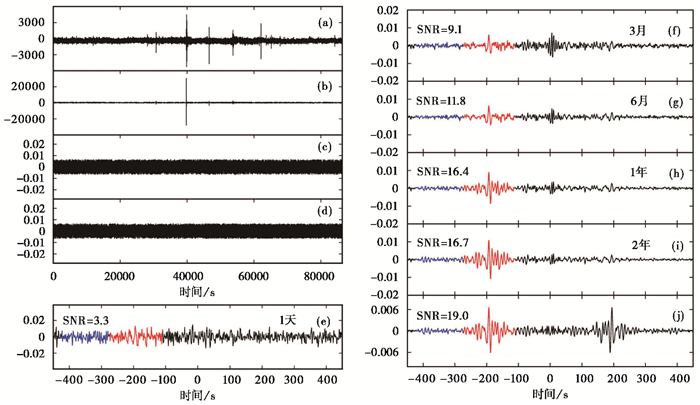
2.1 单台数据预处理

单台数据预处理主要参考Bensen等(2007)提出的方法，包括重采样(1Hz)、去仪器响应、去均值、去趋势、带通滤波(4~60s)、时间域归一化和频谱白噪化。其中，时间域归一化在单台数据预处理中尤为重要，本文采用滑动绝对平均法进行处理，可以有效降低地震信号、仪器异常信号和台站附近非平稳噪声源的影响。图 2(c)、(d)分别给出了商南(SHNA)和淮北(HBE)2个单台数据预处理后的波形，对比图 2(a)、(b)可以看出，地震信号及异常信号得到有效去除，得到了较为“纯净”的噪声信号。

2.2 互相关计算与叠加

单台数据预处理后，对研究区内所有台站每日的连续波形数据在相同时间段内做两两互相关计算，再将2年互相关波形进行叠加，以获取台站对的最终互相关函数，即经验格林函数。图 2(e)~(i)给出了不同时长互相关波形叠加结果，从图中可以看出，随着叠加时长的增加，互相关函数的信噪比随之增加，面波信号也随之凸显。对任意2个台站背景噪声数据做互相关运算，均会得到正、负2个分支，而这2个分支往往呈现非对称性。研究表明，台站附近噪声源的非均匀分布，是引起互相关波形正、负分支非对称性的主要原因(Stehly et al，2006；李昱等，2010；王琼等，2014)。为降低噪声源非均匀分布的影响，本文做了正、负分支反序叠加处理。前人研究表明，互相关波形正、负分支反序叠加，能有效提高互相关函数的信噪比(Lin et al，2008；Zheng et al，2008)，对比图 2(i)、(j)可以发现，正、负分支反序叠加后的信噪比由16.7提高到19.0。图 3给出了部分台站对互相关波形2年叠加后再经正、负分支反序叠加的结果，从图中可以看出，互相关波形呈对称分布，且面波信号明显，从而为进一步提取群速度频散提供了可靠的数据保障。

2.3 群速度频散曲线测量及质量控制

采用多重滤波技术对瑞利波群速度的频散曲线进行提取，在提取过程中借助了姚华建等(2004)基于图像分析方法编制的软件，该软件实现了群速度频散曲线的全自动快速批提取。图 4给出了焦作(JZ)和麻城(MCH)台站对的群速度频散曲线提取示意图。为确保群速度频散曲线提取的可靠性，本文基于经验格林函数信噪比和台间距条件对频散测量进行质量控制。不同周期下的信噪比(SNR)定义为该周期下面波信号窗口振幅最大值与噪声信号窗口振幅平均值之比(图 4(a))。面波信号(图 4(b)中红色波形)窗口通过预设瑞利波群速度范围(本文取2~5km/s)来截取，噪声信号(图 4(b)中蓝色波形)窗口取面波信号窗口后150s。研究表明，SNR≥5便可获得可靠的频散测量结果(郭瑛霞等，2017；张丽娜等，2018)，因此本文剔除了信噪比小于5的频散点。此外，为满足远场近似条件，只保留了台间距大于等于3倍波长的频散数据。

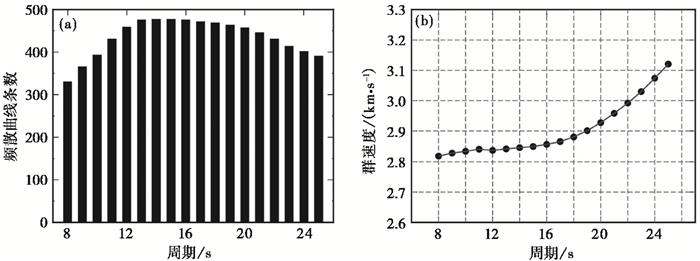
尽管本文研究使用了39个地震台站数据，理论上可以提取741条群速度频散曲线，但为了确保反演结果的可靠性，通过对频散数据提取进行SNR≥5和台间距大于等于3倍波长的质量控制，最终获得了498条群速度频散曲线，用于瑞利波群速度反演。图 5给出了不同周期反演所用射线路径统计和各周期群速度平均值，图中射线路径最少周期(8s)也在330条以上，从而确保了反演结果的可靠性。图 6给出了4个典型周期(8s、14s、20s、25s)射线路径分布情况，图中除研究区边缘射线密度较低外，整体覆盖良好。

2.4 瑞利波群速度层析成像

采用基于连续模型的最小二乘反演方法(Tarantola et al，1982；Montagner，1986)进行瑞利波群速度层析成像。目标函数Φ(s)参考Yao等(2006)给出的公式

$ \mathit{\Phi} \left(s \right) = {(t - {t_{{\rm{obs}}}})^T}C_{\rm{D}}^{ - 1}(t - {t_{{\rm{obs}}}}) + {(s - {s_{\rm{p}}})^T}C_{\rm{M}}^{ - 1}(s - {s_{\rm{p}}}) $

(1)

其中，t和t_obs分别为预测群速度走时和观测群速度走时，s和s_p分别为预测群速度慢度和先验群速度慢度，C_D和C_M分别为数据和模型协方差矩阵。模型空间的协方差为

$ {C_{\rm{M}}}({r_1}, {r_2}) = {\sigma ^2}_s{\rm{exp}}\left({ - \frac{{{{({r_1} - {r_2})}^2}}}{{2{L^2}}}} \right), {\sigma _s} = {\rm{ }}\frac{{{\sigma _c}}}{{c_0^2}} $

(2)

式中，σ_s表示先验慢度的不确定性，σ_c表示先验群速度的不确定性，L表示模型参数的空间相关长度。经过大量试算及数据残差分析，本文最终确定各周期瑞利波群速度反演的计算参数为：σ_c取各周期群速度平均值的6%，c₀取各个周期群速度平均值，L=max(50km，c₀T/2)。在群速度层析成像中，采用1°×1°的网格对研究区划分，最终得到了8~25s的瑞利波群速度分布图像。

3 分辨率检测

采用检测板测试法对群速度层析成像结果的空间分辨能力进行检测。其原理是通过给定不同周期瑞利波群速度理论模型，按实际射线分布计算理论走时，并对理论走时加上一定的随机误差，得到合成数据，再使用与实际数据反演相同的方法和控制参数进行反演，最终分析反演结果能否恢复理论速度模型。

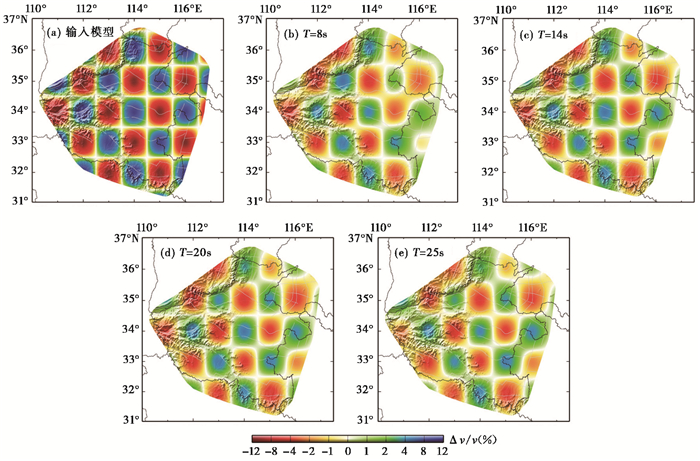
根据检测板测试原理，对研究区进行了1°×1°的网格划分，并在不同周期瑞利波群速度平均值基础上添加±12%的扰动量作为输入模型，按实际射线路径计算理论走时并加上1%的随机误差构成合成数据，最后反演合成数据获得不同周期的检测板测试结果。图 7给出了输入模型(在相对色标(Δv/v，单位：%，其中v表示速度)下，不同周期输入模型扰动样式和幅度相同)和8s、14s、20s、25s的检测板测试结果。结果表明，射线覆盖直接影响反演结果的分辨率，除射线分布稀疏区域的扰动样式和幅度恢复相对较差外，其它大部分地区的分辨率均能达到1°×1°，扰动样式和幅度均可基本恢复，因此本文采用1°×1°进行网格划分是合理的，其成像结果比较可靠。

4 结果和讨论

根据上述群速度层析成像方法，最终获得了河南及邻区8~25s的瑞利波群速度分布图像。前人研究表明，某一周期的群速度对1/3波长深度的剪切波速度结构最为敏感(Lin et al，2007；Yang et al，2007)，不同周期的群速度分布分别表征了不同深度范围内的构造差异(房立华等，2009；高东辉等，2011)。根据各周期群速度分布特征，本文选取了4个典型周期的群速度分布图像(图 8)进行讨论。

周期为8s的群速度分布图像(图 8(a))主要反映地壳浅层速度结构特征。该周期低速异常分布于华北平原；高速异常分布于太行山、崤山、熊耳山、伏牛山、外方山、桐柏山和大别山。山区与平原高、低速分布界限明显，其分布特征与山脉和平原构造有一定相关性。低速异常主要由平原沉积层引起，高速异常主要由造山带结晶基底引起。值得注意的是，有沉积层覆盖的南襄盆地并未观测到明显低速异常，这可能与研究区边缘射线覆盖较低、分辨率不高有关。

周期为14s、20s的群速度分布图像(图 8(b)、(c))对中上地壳结构较为敏感。14s、20s周期的群速度分布与8s周期在山区地区有相似特征，太行山、崤山、熊耳山、伏牛山、外方山、桐柏山和大别山等仍表现为高速异常，说明山区地区中上地壳与地壳浅部结构有一定的相关性和继承性。华北平原地区表现为低速异常，且低速异常范围从14s开始有所减小，到20s进一步减小并呈现高、低速异常交错分布的特征，这一现象在叶庆东等(2014)研究结果中也有所体现。

周期为25s的群速度分布图像(图 8(d))反映了下地壳速度结构变化。该周期群速度分布受莫霍面起伏影响较大。大致以太行-武陵重力梯度带为界，西部表现为低速异常，东部至研究区中部以高速异常为主，体现了地壳东薄西厚的结构特征。华北平原地区地壳厚度为31~35km，是减薄大陆地壳(徐纪人等，2003；徐纪人等，2004)，施程成等(2014)的噪声层析成像结果显示华北平原moho面深度较中西部地区浅，因此在地壳相对较薄的华北平原地区，该周期却表现为大范围低速异常，这可能体现了减薄大陆地壳的结构特征，与吴萍萍等(2015)的研究结果基本一致。

5 结论

本文利用河南及邻区39个宽频带和甚宽频带地震台站2年(2014年1月~2015年12月)的连续波形数据，通过近年来新发展的噪声层析成像方法获得了河南及邻区8~25s的瑞利波群速度分布图像，反演结果揭示了河南及邻区地壳结构的横向不均匀性。地壳浅层的高、低速分布与沉积层厚度、结晶基底埋深等区域地质构造密切相关，平原地区表现为低速异常，山区表现为高速异常。山区地区在中上地壳表现出的高速异常与地壳浅层相似，说明中上地壳与地壳浅层结构有一定相关性和继承性。华北平原地区在中上地壳存在低速异常随周期增加而减小的现象。华北平原地区在下地壳表现出的低速异常，可能与大陆地壳减薄有关。大致以太行-武陵重力梯度带为界，下地壳表现出的西部低速、东部至研究区中部高速异常差异，体现了地壳东薄西厚的结构特征。

本文获得的河南及邻区地壳群速度分布，为进一步获得该地区地壳剪切波速度结构奠定了基础。随着2018年河南省地震局各市、县台及邻省共享台站的接入，台网密度实现了大幅提高，这将为进一步开展河南及邻区更高精度的地壳结构研究提供充足的数据保障，而高精度的地壳结构信息，将对研究河南及邻区区域构造活动及探讨地震分布和成因等具有一定意义。

致谢: 本文使用了梁春涛博士提供的背景噪声数据处理程序以及姚华建博士提供的频散提取及面波反演程序，河南省地震局为本文提供了连续波形数据，在此一并表示感谢。