0 引言

据中国地震台网中心(CENC)测定：2019年5月26日15时41分(北京时间), 秘鲁北部发生M7.8地震, 此次地震震中位于5.85°S、75.18°W, 震源深度为100km。该地震是2019年1月1日以来在全球范围内规模最大的一次地震, 也是秘鲁地区12年以来规模最大的一次地震。地震所在区域的地震活动极其活跃, 2019年3月1日, 震源区附近曾发生M7.0地震(14.58°S, 70.05°W)。尽管此次地震震级较大, 但由于其属于中深源型地震, 此次强震仅造成1人死亡和11人受伤, 50多间民房被毁。根据欧洲地中海地震信息中心(EMSC)收到的报告, 秘鲁以及包括厄瓜多尔、哥伦比亚、巴西等在内的周边多国有震感。由于此次地震发生在内陆地区, 据太平洋海啸预警中心(PTWC)报道, 此次地震未能产生海啸。

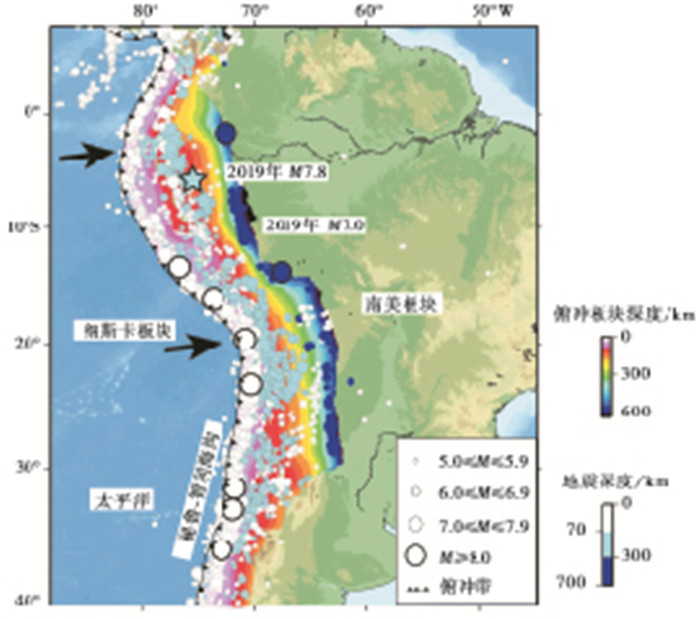
秘鲁M7.8地震震中位于纳斯卡板块向南美板块俯冲的秘鲁-智利海沟北部区域。纳斯卡板块是太平洋东部的一个相对年轻的板块, 构造活动剧烈。该板块以每年约66mm的速率向东俯冲至南美板块之下(Kendrick et al，2013；崔清辉等, 2017), 板块的俯冲导致了安第斯山脉隆起, 秘鲁丘陵形成火山, 且2个板块之间存在一条巨型的秘鲁-智利海沟。由于板块的俯冲作用以及俯冲板块空间几何分布不规则, 导致俯冲角度不尽相同, 使得该地区地震深度呈现浅源、中源和深源3种类型。俯冲带内的浅源地震包括浅源板间和板内地震, 而中源和深源地震皆为板内地震。海岸和海沟处的地震多为浅源地震, 活动频繁且破坏性地震较多。据美国地震信息中心(NEIC)提供的历史地震目录显示, 自1900年以来, 沿秘鲁-智利俯冲板块界面发生了7次8.0级及以上地震(图 1), 这些地震大多为板间浅源地震, 这些地震容易引发破坏性海啸(Okal et al，2006)。由图 1可知, 该区域的中深源地震强度明显小于浅源地震, 本次地震是该地区发生的一次震级最大的中深源地震。由于纳斯卡板块持续向南美板块下俯冲, 地震最深深度达630km, 相比浅源地震而言, 深源地震的强度和频率明显降低。

大量的研究表明, 地震破裂过程对理解强震破裂方式和尺度以及断层错动方式和震源区介质性质的非均匀性均有重要的现实意义, 同时也有利于判断断层活动特征及未来强余震的发展趋势, 可为震后快速判定灾害情况及救灾工作提供依据(王琼等, 2015；赵翠萍等, 2009；刘成利等, 2014)。因此, 为更好地得到秘鲁M7.8地震的破裂过程, 我们首先采用W震相方法(Kanamori et al，2008), 得到此次地震的断层面几何参数、地震矩、矩心位置、矩心深度等震源特征参数。随后, 采用远震体波有限断层模型(Kikuchi et al, 1982、1991、1993)反演破裂面上的滑移量分布以及破裂尺度、破裂方向等有限震源模型参数。本研究结果可为今后大震应急产品工作产出提供有意义的经验积累, 同时也为研究秘鲁地区的地震活动特征和孕育机制提供初步科学参考和依据。

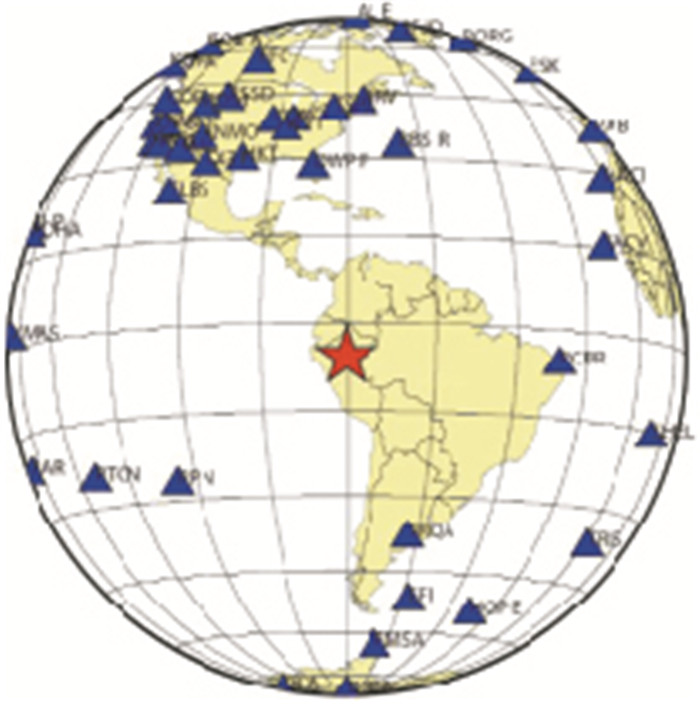
1 资料与方法

本研究采用美国地震学研究联合会数据管理中心(IRIS/DMC)提供下载的全球数字地震台网(GSN)记录的宽频带垂直分量地震波形数据, 选择震中距为5°~85°内47个台站进行矩张量解和有限断层震源破裂过程快速反演, 由台站分布情况(图 2)可看出, 台站围绕震源处有较好的分布, 反演时速度模型均采用AK135全球一维走时速度模型。

本文采用W震相求取矩张量解的方法反演得到最佳断层面解。由于W震相是P波和S波之间斜坡状的长周期震相(100~1000s), 其能量为P、PP、SP和S等多个震相的叠加, 该震相比传统的面波速度快, 且振幅不易被裁剪, 适用于较大震级地震快速测定震源参数, 为大地震应急救灾和海啸预警服务(梁姗姗等, 2018)。反演过程中, 参考Duputel等(2012)给出的M_W8.0以上地震滤波参考范围, 采用0.001~0.005HZ带通滤波器对波形数据进行滤波处理, 选取初至P波后15倍震中距(单位为°)的时间窗(单位为s)自动提取W震相。基于中国地震台网中心所测定的地震基本参数(包括发震时刻、震中经纬度、震源深度和震级)作为初始值, 采用AK135全球一维走时速度模型计算的格林函数, 基于简振正型叠加方法计算理论波形。

由W震相反演未知震源参数向量m可表示为

$ {\boldsymbol m} = \left({\frac{{\boldsymbol f}}{{{{\boldsymbol \eta} _c}}}} \right) $

(1)

其中, 地震矩张量f =[M_rr, M_pp, M_tt, M_rp, M_rt, M_pt]^t表征质心时空坐标η_c=[θ_c，Φ_c，h_c，τ_c]^t, 参数θ_c，Φ_c，h_c和τ_c分别表示质心余纬度、质心经度、质心深度及质心相对发震时刻的时间偏移。式(1)中共包含10个未知参数。

为了确定最佳的质心时空坐标η_c, 可以通过网格搜索法, 使得定义的误差函数最小

$ \chi \left({\boldsymbol m} \right) = \frac{1}{2} \cdot \left({{{\boldsymbol S}_w}\left({\boldsymbol m} \right) - {{\boldsymbol d}_w}} \right)\left({{{\boldsymbol S}_w}\left({\boldsymbol m} \right) - {{\boldsymbol d}_w}} \right) $

(2)

其中, 向量S_w表示W震相的理论波形, 向量d_w为W震相的实际波形。

在确定秘鲁M7.8地震的发震断层面解参数后, 我们采用Kikuchi等(1993)提出的非负最小二乘法(NNLS)来反演此次地震的地震矩及其静态滑移量分布。该方法基本思路为：首先对视震源时间函数的形状做出假设, 通过反演得到其幅值, 同时以震源时间函数为基础, 分割出子事件并反演出子断层的时空参数, 最终得到整个事件的空间位置和滑动分布(冀战波等, 2014；赵翠萍等, 2013)。通过多次计算尝试, 将发震断层划分为14×8个单位面积13km×13km的子断层, 将每个子断层近似看作位于子块中心的点源, 破裂速度设为2.5km/s, 光滑约束权重因子设为1.0。在反演过程中, 对波形拟合不好的台站进行降权处理, 以调整该台站波形记录数据参与计算的权重。采用平面层状介质模型的广义反射、透射系数矩阵法计算47个台站的格林函数(Kennett et al，1979；李飞等, 2017)。同时, 对所有波形数据和计算得到的格林函数进行滤波处理, 考虑到震源破裂过程的细节信息包含在高于拐角频率的波形里, 采取的滤波频带为0.01~0.5HZ。其反演基本原理如下。

假设在点源位错模型下, 远程点源位移可以近似表达为

$ {U_i}\left({r, t} \right) = {G_{ij, k}}\left({r, t} \right) * {M_{jk}}\left(t \right) $

(3)

其中, U_i(r，t)为t时刻r处的位移在i方向的分量；G_ij，_k(r，t)为反映介质传播效应的格林函数；M_jk (t)为地震矩张量, 由于地震震源的角动量守恒, 实际上矩张量只有6个独立分量。

在进行平面有限断层的震源破裂过程反演时, 通常将断层划分为N个子断层, 每个子断层都视为1个点源, 某一观测点在某一时刻的理论位移为所有子断层在此观测点产生的位移叠加, 运用线性叠加原理, 并在等式两边同时与台站的仪器响应进行褶积, 则得到台站i的远场位移表达式

$ D'\left( t \right) = \sum\nolimits_{j = 1}^N {{M_j}{s_j}\left( t \right) * } G_j^i\left( {t - {\tau _{ij}}} \right) $

(4)

其中, D′(t)为台站i包含仪器响应的远场地震位移记录, M_j为子断层j的地震矩, s_j(t)为子断层j的远场震源时间函数, G_jⁱ(t)为台站i对子断层j破裂产生包含仪器响应的格林函数, 每个台站在每个时间点的理论位移, 是每个子断层在该台站产生的理论地震图的叠加。

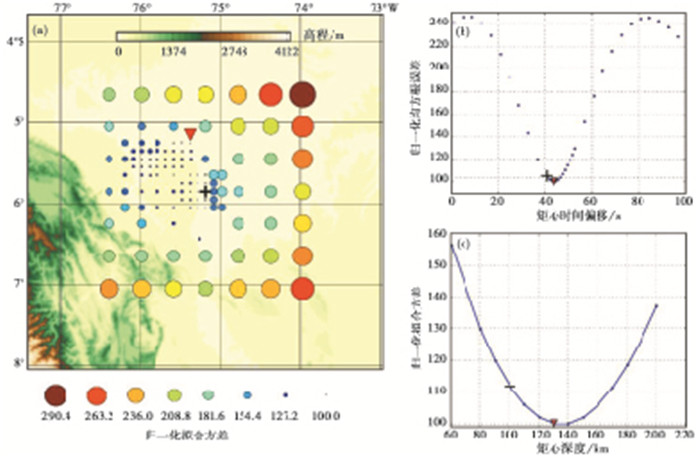
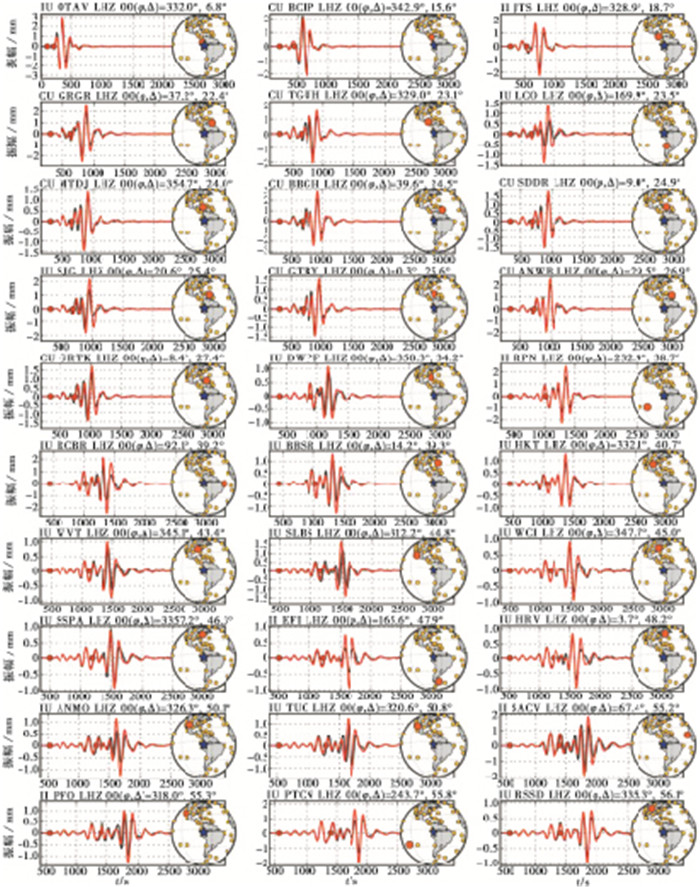
2 结果 2.1 矩张量解反演

经过多次反复迭代, 最终反演得到秘鲁M7.8地震的矩张量解和相关震源特征参数。通过网格搜索法获得最佳矩心水平位置、矩心时间偏移和矩心深度(图 3), 其中, 断层面节面Ⅰ走向348.9°/倾角60.9°/滑动角-84.7°；节面Ⅱ走向158.2°/倾角29.5°/滑动角-99.4°, 矩震级M_W8.0, 所得到矩心位置为(75.28°W, 5.25°S), 相比初始破裂点(75.18°W, 5.85°S)向NNW方向偏移约81km(图 3(a)), 矩心深度为123km, 比破裂起始深度略深。通过台站记录到的观测波形与W震相获得的矩张量解拟合波形对比(图 4), 可以看出大部分波形拟合较好, 波形拟合均方根误差仅为0.053。为更好地评价本研究结果的可靠性, 采用最小空间旋转角(万永革, 2019；万永革等, 2019)来衡量本研究结果与其他研究机构的差别, 选取本研究得到的矩张量解为参考解, 计算其与其他三家机构的最小旋转角, 由表 1可以看出最小旋转角在5.4°~8.9°之间, 变化范围不大, 这也验证了本文矩张量解反演结果的可靠性。本研究和其他三家地震机构一样, 均显示出该地震为一次正断型为主事件。

由矩张量反演结果可知, 水平最大主压应力为近EW向, 平行于海岸线方向。我们认为此次地震的发生与海洋板块内部变形有关, 推测该地震可能由于正在向下俯冲的纳斯卡板块产生规模巨大的伸展变形所致, 而该伸展应力实际上是由密度更为致密的下沉板块的重力牵引造成的(Dorbath et al，1990)。

2.2 基于有限断层模型的破裂过程反演

在破裂过程反演中, 一般需要借助区域地质构造、余震分布和多普勒效应等判断真实断层节面(张勇等, 2014)。由图 1可知, 由于纳斯卡板块持续向东俯冲到南美板块之下, 我们认为南美板块为断层的上盘, 而纳斯卡板块为断层的下盘, 相应的断层走向与节面Ⅰ走向一致。因此, 推断此次地震的发震断层节面为NNW向(走向349°), 倾向为ENE向(倾角61°)。

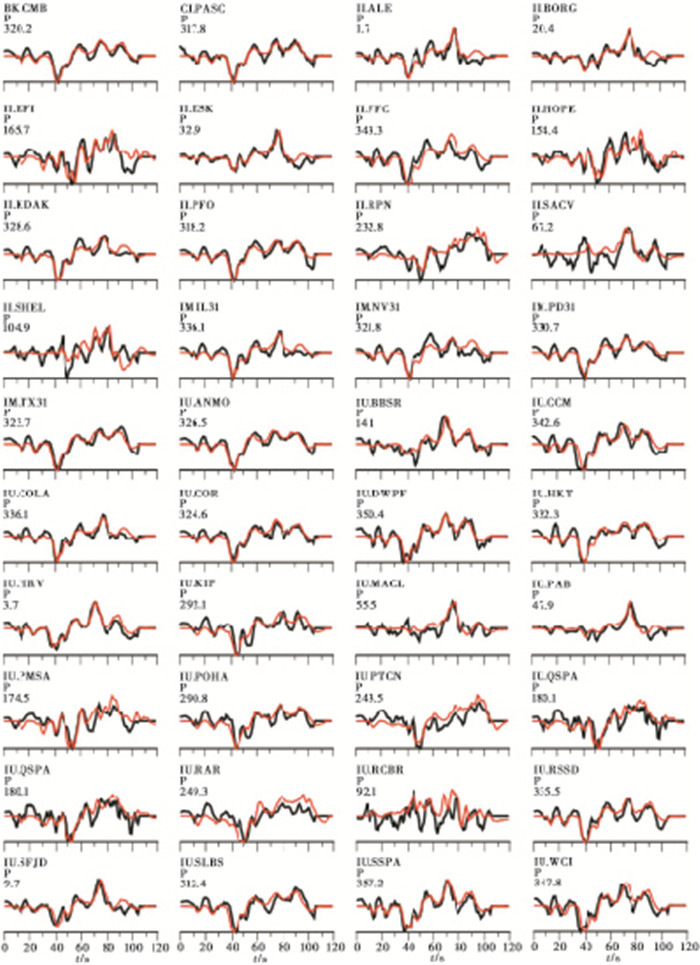
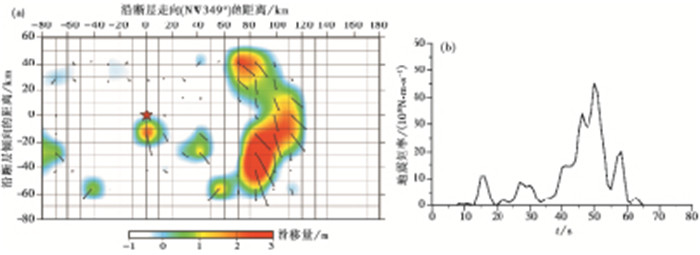
基于本研究矩张量解所得到的断层几何参数, 反演得到本次秘鲁地震的震源破裂过程。反演结果的理论地震图与实际观测垂直向记录拟合如图 5所示, 由图 5可以看出, 基于有限断层震源模型计算得到的理论位移与观测资料能较好地吻合, 证明了远场反演结果的可靠性与稳定性。从反演得到的断层面分布来看(图 6), 断层破裂从初始破裂点开始, 从震中主要向WN向延伸破裂, 并显示深部破裂的特征, 最终形成的滑动区域集中在140km×200km的上地幔内, 最大位移在震中NNW方向, 最大位移量约3m, 除此之外, 断层沿走向的方向上的两侧有一些滑动零星分布, 但规模不大。此次地震释放的标量地震矩为0.-539×10²¹N·m, 相当于矩震级为M_W7.8, 略小于本研究矩张量解反演所得到的M_W8.0。此外, 模型结果显示此次地震破裂时间为70s, 在40~60s时释放了整个地震80%的地震矩, 主要破裂区域在震后40s才开始形成, 在40s之前, 破裂的集中程度和地震矩释放的规模均较弱, 断层在破裂开始后逐渐加速破裂, 约50s时地震矩释放速率达到峰值, 60s后破裂迅速愈合(图 6(b))。图 7为发震断层滑动分布地表投影示意图, 由图 7可以看出, 此次地震破裂过程相对简单, 但破裂最大量并不在震中附近, 而是在震中北偏西约80km处的2次破裂, 其中更靠N方向的破裂幅度更大一些, 最大滑动量达到3m。将本研究反演所得到的矩心位置和GCMT所得矩心位置同时标注在滑动分布地表投影示意图上(图 7), 两者结果均显示出破裂中心位置相对于初始破裂位置向NNW方向偏移, 本研究的结果与破裂滑移面的最大位移滑移处更为接近, 与断层最大滑移量分布具有更好的相关性。

地震发生后, 美国地质调查局(USGS)在第一时间给出根据有限断层模型得到的震源破裂过程图像。本研究滑动分布结果整体与美国地质调查局结果有较好的一致性, 均是沿断层走向60~80km处的滑动位移最大, 所不同的是本研究结果显示出在最大位移处有2次破裂, 而美国地质调查局结果仅为1次破裂, 且最大滑动量有所差异, 美国地质调查局最大滑动量仅为2.3m。造成本研究与USGS在滑移量和破裂次数差异的原因可能是选取资料和反演约束的不同。

3 讨论与结论

本文使用IRIS全球数字地震台网记录的宽频带波形数据, 采用W震相矩张量解反演方法和有限断层模型反演方法快速得到秘鲁北部M7.8地震的破裂过程。矩张量解反演结果表明此次地震是一次正断型为主的事件, 矩心深度约123km, 断层面节面Ⅰ走向348.9°/倾角60.9°/滑动角-84.7°；节面Ⅱ走向158.2°/倾角29.5°/滑动角-99.4°, 矩震级为M_W8.0, 获得的矩张量解结果与其他研究给出的结果基本一致。

结合震源区区域构造背景, 初步认为节面Ⅰ为此次地震的发震断层面, 即NNW向(349.0°), 节面倾角为60.9°。我们认为此次地震的发生与海洋板块内部变形有关, 推测该地震可能由正在向下俯冲的纳斯卡板块产生规模巨大的伸展变形所致。

基于NNW走向断层模型, 得出此次地震释放的标量地震矩为0.539×10²¹N·m, 相当于矩震级为M_W7.8。此次地震的初始破裂点在滑动区域的边缘, 最大滑移量约3m, 位于震源NNW方向且深度在140~180km的上地幔内, 破裂主要发生在深部区域, 这也许能解释如此大震级的地震并未造成大量人员伤亡和巨大损失的原因。从地震破裂的时间演化过程来看, 整个地震的破裂持续时间较长, 约为70s, 地震能量主要集中在震后40~60s释放出来。

本次地震的发生反映了秘鲁断裂的主要构造活动过程, 推测该地震可能由正在向下俯冲的纳斯卡板块产生规模巨大的伸展变形所致, 受到俯冲板块相对弯曲的控制而产生的张性破裂, 而该伸展应力实际上是由密度更为致密的下沉板块的重力牵引造成的。本研究针对此次秘鲁地震, 求取震源机制解, 探讨震源破裂特征, 为理解大地震的发震机制和孕育机理提供科学依据。震源机制和震源破裂特征反演不仅有助于认识震源物理特征, 而且对地震防灾减灾有重要的现实意义。特别是大地震发生后, 可以根据断层面反演结果和已有地震构造背景, 识别真实发震断层面, 快速确定地震破裂过程, 为地震救灾响应和进一步的地震趋势研判提供有益帮助。

致谢: 本研究使用的数字波形数据均来自国际地震学联合研究会数据管理中心(IRIS/DMC), 在此表示感谢。