0 引言

地电阻率观测从最初的土地电观测到现在的数字观测系统, 已有三十多年的历史, 目前整个观测系统已较成熟。地电阻率观测作为前兆观测存在几个特点：观测系统具备完善的标定和检查装置, 探测的物理量独立于电极(探头), 最大的探测深度可以达到400~500m, 探测对象为一定体积范围内的视电阻率, 观测物理量的前兆意义明确, 具备场兆和源兆不同表现的物理识别。基于以上几点, 地电阻率观测的真实性、可重复性、具备一定范围和深度等特征具备了作为前兆现象观测的一些重要要素。经过三十多年的发展, 目前全国已有80多个地电阻率观测数字化观测场地, 积累了大量的观测资料, 在很多中强震和大地震前可以发现一些突出的中短期异常, 很多学者均做了相关方面的工作。陆阳泉等(1980、1990、1998)、陈大元等(1992)、张洪魁等(1996)进行了岩石破裂物理实验, 给出了破裂过程中地电阻率的变化过程；钱复业等(1982、1990、1998)、钱家栋(1993)、钱家栋等(1998、2013)、王志贤(1990)、杜学彬(2010)对全国各地地电阻率的一些震前变化做了系统的整理, 给出了地电阻率异常形态、幅度、异常时间与地震的关系；沈红会等(2017)认为地电阻趋势变化与周围区域应力场的相对变化有关。综上所述, 在三十多年的地电阻率观测和研究中, 前人对地电阻率观测的观测机理、影响因素、震例总结等方面均做了很多详细的分析, 肯定了地电阻率在地震预报中的预测意义, 也给出了利用地电阻率预测地震的一些研究方法和指标建设。本文结合前人的研究成果, 对江苏地区的地电阻率预测指标进行探讨。

1 地电阻率观测结果的机理分析

一般地电阻率观测采用对称四极法, 观测对象为地下一定体积内的视电阻率, 探测深度由供电极距和地下电性结构决定(钱家栋等, 1985)。对于层状介质有

$ \frac{{\Delta {\rho _{\rm s}}}}{{{\rho _{\rm s}}}}{|_{AB}} = \sum\limits_{i = 1}^n {{S_i}} \frac{{\Delta {\rho _i}}}{{{\rho _i}}} $

(1)

其中, ρ_s为观测电阻率, ρ_i为各层电阻率, S_i为各层电阻率的影响系数。

在实际观测中, 观测层一般为非饱和水与饱和水岩石, 每一层的电阻率可以由独立的Archie定律计算得出

$ \rho = {\rho _o}{{\mathit \Phi} ^{ - m}}{\theta ^{ - n}} $

(2)

其中, ρ_o孔隙流体电阻率, m、n为结构常数, 一般在1~2之间, θ为岩石水饱和率。根据式(1)、(2), 可以认为影响地电阻率观测结果的主要因素为影响系数S_i、孔隙度Φ和岩石水饱和率θ。其中, 影响系数S_i在装置建设完成后已基本确定, 体现了各层电阻率的权重影响, 一般在观测中不作为变量进行考虑, 因此, 在实际观测中, 主要考虑孔隙度Φ和岩石水饱和率θ的影响。下面分非构造活动和构造活动两方面进行讨论。

(1) 非构造活动

非构造活动主要指降雨、灌溉、注水、抽水等, 为非前兆性影响, 一般孔隙度不易变化, 主要考虑饱和率的影响。在实际观测中, 表层土壤或岩石的水具有不饱和性, 降雨、灌溉等表层水位变化引起土壤或岩石的饱和度变化, 表层电阻率下降, 从而通过式(1)中的影响系数S₁或S₂对表层电阻率造成影响：S₁或S₂为正值时, 表现为短期下降变化或正年变变化, 反之为短期上升变化或负年变变化。在含水层以下的土壤或岩石一般趋于饱和, 因此深层注水或抽水一般对岩石饱和度改变较小, 对地电阻率观测结果影响不大。在实际观测中，华东地区大部分地区均存在深层采水或注水现象, 深层水位观测表现为单向的长年趋势变化, 周围的地电阻率长期观测结果与水位观测结果的长趋势变化并不一致, 因此, 非构造活动下的深部水位变化对地电阻率观测结果影响不大。因此, 在非构造活动下, 目前影响地电阻率观测的主要是表层降雨、灌溉等(场地内的金属管线、漏电、周围铁气化铁路等可以理解为单一环境性干扰)。

(2) 构造活动

马瑾等(1995)根据岩石变形不同阶段的应力特征, 把震前分为线性、屈服和失稳阶段3个阶段, 不同的阶段对应不同的岩石力学特征, 表现为不同学科的前兆异常。从应力场变化特征来看, 这3个阶段可以理解为线形应力变化阶段、应力变化转折阶段和应力释放阶段(失稳阶段)；从介质变化特征来看, 则主要体现在岩石裂隙的变化, 即裂隙的收缩或拉张阶段、裂隙导通阶段、裂隙的大幅扩容扩散阶段；从地电阻率观测结果来看, 主要表现为接近线性的长趋势变化、趋势转折、大幅度下降变化(破年变变化), 这一过程和很多的实验室岩石破裂实验非常一致。震前岩石变形不同阶段主要指震源断层的变化, 3个阶段中线性阶段和屈服阶段是可逆的, 而失稳阶段是不可逆的, 因此, 在非震源区, 只能观测到线性阶段和屈服阶段, 在实际观测中, 尤其是地震震级较小的情况下, 大部分观测点并不在震中区, 很多前兆只是岩石变形的线性阶段和屈服阶段的表现。根据上述分析可知, 地电阻率的前兆可以分为2种异常变化, 一种是无论在震源区或非震源区均可以观测到的趋势变化和趋势转折, 二是和震源有关的大幅度下降变化(破年变变化)。长期的趋势变化主要与应力场变化有关, 根据赵玉林等(1990)的实验研究结果得到岩石形变与电阻率的关系

$ K = \left( {\Delta \rho /\rho } \right)/\left( {\Delta V/V} \right) $

(3)

式中，ΔV/V为应变量。在岩石形变的线性阶段, 地电阻率一般表现为趋势的上升或下降变化；在岩石形变的屈服阶段, 周围应力变化出现趋势转折, 相应的地电阻率一般也会出现趋势转折变化；但震源附近(或局部岩石破裂敏感区域)出现介质裂隙的扩容扩散后, 由于裂隙水的大量导通, 岩石电阻率会出现明显的下降变化。

综合以上分析, 地电阻率的前兆异常表现为两类异常变化, 一是构造活动下的长期趋势变化, 反映周围区域应力场的变化, 与周围地震存在一定的对应关系, 但一般不存在明确的一一对应关系, 与水位、形变等观测反映的应力变化具有一定的同步性；二是震源附近的快速变化或破年变变化, 一般为下降变化, 和地震存在明确的一一对应关系。

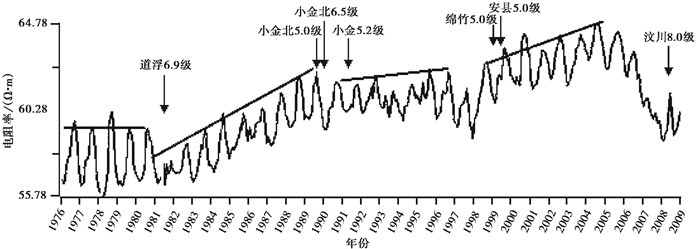
以成都台观测结果对以上3类变化进行分析。图 1为成都台地电阻率SN向1976~2008年的月均值曲线, 长期观测结果基本包含了以上三类变化, 一是具有明显的年变化特征, 主要为季节因素造成的表层地电阻率变化；二是地电阻率的长期变化基本上是趋势向上的, 龙门山断裂带受西北巴彦喀拉活动地块的挤压是一个长期的单向过程, 在这个过程中, 龙门山断裂带不断重复应力积累和释放的过程, 地电阻率的长期趋势向上反映了周围长期应力积累的过程, 而周围200km范围内的地震均是发生在趋势转折的位置；三是在2008年5月12日的汶川M_S8.0地震前, 从2006年下半年开始出现了明显的破年变加速下降异常, 考虑到震中距仅约69km, 可以认为是震源的变化引起的。

无论是长期近似由西向东单一方向的应力挤压还是汶川地震前岩石破裂后的裂隙扩容, 成都台地电阻率的观测结果均与很多实验室的实验过程非常接近, 因此表现出的观测结果也和实验室的结果基本一致。在实际观测中, 全国大部分地电阻率观测结果则未必能清晰地展示这一过程, 主要原因是周围应力场的相对变化方向可能仅几年就会发生变化, 另外, 在有限的观测期间, 大部分观测场地均较难位于某次地震的震源区或应力反应的敏感区。依据大部分观测场地的观测结果, 结合构造作用下地电阻率的变化, 综合考虑地电阻率的预测指标, 可以给出两类异常指标, 一是与震源区的变化直接相关的下降或破年变变化；二是一年以上的趋势变化并出现转折。下面梳理了江苏1980年以来5个地电阻率场地观测结果, 对地电阻率的预测指标做进一步讨论和验证分析。

2 江苏地电阻率场地震例分析 2.1 选取资料

选取江苏5个地震台站(南京台、高邮台、江宁台、新沂台、海安台)自1981年以来的直流地电阻率观测数据, 考虑到在30多年的观测中, 各台站的观测场地均多次变更, 观测数据连续性差, 并且部分时段场地的数据受干扰较多, 因此选择观测场地5年以上连续观测相对比较可靠的数据进行计算分析。分析地震为1981年以来江苏及邻区300km范围内M≥4 4地震(表 1)。

2.2 计算方法

主要采用距平或傅氏滑动方法去年变(计算方法略)。由于大部分观测场地均存在明显的年变, 因此无论是分析破年变变化还是长趋势变化, 一般观测数据应先进行去年变分析, 本文计算过程均采用日均值数据进行傅氏滑动分析去年变, 然后采用归一化速率方法建立预测指标。

相对速率方法以一定的步长对日值曲线计算曲线对时间轴的斜率, 并通过相对均值进行归一化, 观测数据曲线对时间轴的斜率可以表示为

$ {k_i} = \frac{{\sum\limits_{j = 1}^n {{T_j}\sum\limits_{j = 1}^n {{y_j} - n\sum\limits_{j = 1}^n {{T_j}{y_j}} } } }}{{{{\left( {\sum\limits_{j = 1}^n {{T_j}} } \right)}^2} - n\sum\limits_{j = 1}^n {T_j^2} }} $

(4)

自相关系数为

$ {R_i} = \frac{{n\sum\limits_{j = 1}^n {{T_j}{y_j}} - \frac{1}{n}\left( {\sum\limits_{j = 1}^n {{T_j}} \sum\limits_{j = 1}^n {{y_j}} } \right)}}{{\sqrt {\left[ {\sum\limits_{j = 1}^n {T_j^2} - \frac{1}{n}{{\left( {\sum\limits_{j = 1}^n {{T_j}} } \right)}^2}} \right] \cdot \left[ {\sum\limits_{j = 1}^n {y_j^2} - \frac{1}{n}{{\left( {\sum\limits_{j = 1}^n {{y_j}} } \right)}^2}} \right]} }} $

(5)

归一化速率法序列为

$ {S_i} = {R_i} \times {K_i}/{\sigma _{n - 1}},i = n,n + 1, \cdots ,N $

(6)

其中, n为滑动步长, N为资料长度, σ_n-1为(N-n)个R_i×K_i的时间序列的均值, {y}为等间隔数据时间序列, {T}为相应的等间隔时间序列。本文中采用归一化速率方法计算趋势变化, 计算中均采用365天作为相关、斜率和归一化速率的计算窗长, 步长为1天。

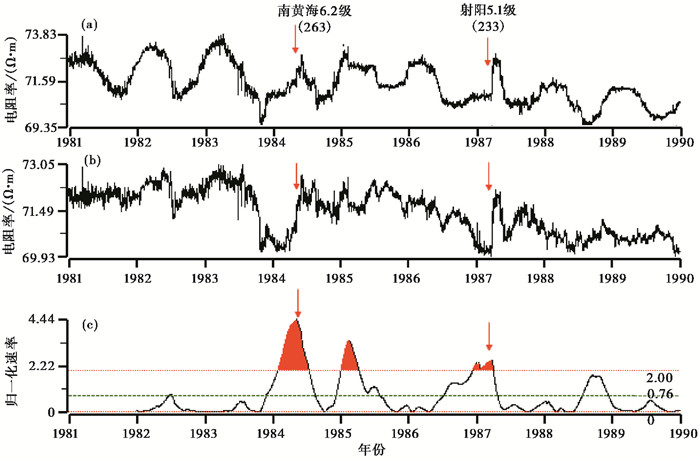
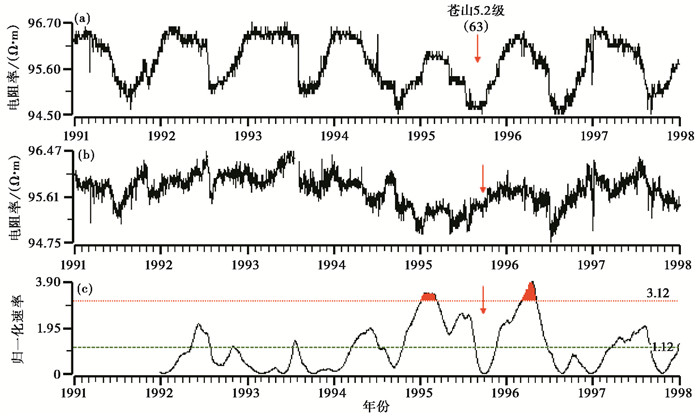
2.3 典型震例 2.3.1 地电阻率的破年变变化

图 2(a)、2(b)为南京台地电阻率EW向1981~1989年的日值和去年变曲线, 图中显示在1984年5月21日的南黄海6.2级地震和1987年2月17日的射阳5.1级地震前, 观测数据出现明显的破年变现象, 去年变后在震前均表现为下降漏斗型异常, 地震发生在漏斗底部或转折恢复时, 2次地震前的异常幅度分别为3.27%和1.92%(沈红会等, 2001)。这2次地震的震源距离南京台分别为263km和233km, 严格来说南京台不在震源区, 一般不在震源附近出现破年变的漏斗型下降的情况较少, 推测南京台观测场地位于某方向应变的敏感区。对去年变数据进行365天归一化速率计算后得到图 2(c)，图中显示2次破年变异常前归一化速率值也出现明显异常, 异常幅度分别为4.4和2.5, 变化速率均超过2倍均方差。值得注意的是, 归一化速率值在1985年初也出现一高值异常, 对比破年变曲线, 很明显这一高值异常是漏斗型异常造成的, 本质上还是和前面的异常为同一性质, 因此不作为新的异常, 由于破年变异常往往下降幅度大, 异常呈现漏斗型, 因此在做归一化速率处理时可能震后也会出现异常, 应注意异常的重复计算。图 3(a)、3(b)为新沂台地电阻率EW向1991~1997年的日值和去年变曲线, 图中显示在1994年年底前出现明显的破年变现象, 去年变后显示在1995年9月20日的山东苍山5.2级地震前, 观测数据表现为下降漏斗型异常, 地震发生在下降转折恢复时, 震前的异常幅度为1.34%。苍山地震的震源距离新沂台为63km, 新沂台地电阻率的下降异常可能与震源有关。对去年变数据进行归一化速率计算后得到图 3(c)，图中显示苍山5.2级地震前归一化速率值出现高值, 超过2倍均方差, 异常幅度为3.3。和图 2类似, 破年变异常往往是漏斗型变化, 因此震后也容易再次出现归一化速率的高值, 但不是新的异常。在下面分析的趋势变化中一般不会出现这种现象。

除了以上3次破年变异常外, 在江苏长期的观测中没有发现更多明显的破年变下降异常, 结合全国的观测结果来看, 破年变下降异常很少被观测到, 一般只在一些大震前, 如1976年唐山7.8级地震、2008年汶川8.0级地震等震前可以明确观测到, 主要与震源区岩石裂隙的微破裂有关, 因此非干扰的破年变的下降异常与周围地震对应关系密切, 一般可以作为地电阻率最可靠的预测指标。在实际观测中更常见的是地电阻率的趋势异常变化。

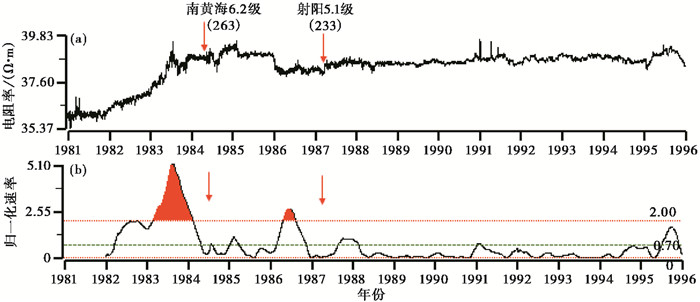
2.3.2 地电阻率的长趋势变化

图 4为1981~1995年南京台地电阻率NS向日值和归一化速率曲线, 图中显示从1981年年底开始观测数据出现趋势上升变化, 1983年8月到达峰值后转平, 上升的最大相对幅度约7.7%, 之后发生了1984年5月21日的南黄海6.2级地震, 震中距为263km；另外, 在1987年2月17日的射阳5.1级地震前, 观测数据出现1年左右的趋势下降变化。从归一化速率曲线来看, 这2次趋势变化速率均超过2倍均方差, 最大归一化速率值分别为5.1和2.7, 震前的异常变化在15年的观测中非常显著。采用同样的方法处理了1989~1998年海安台SN向的数据(图 5)。

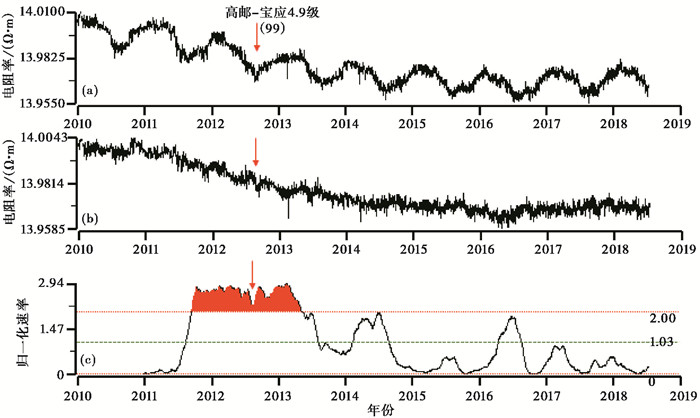
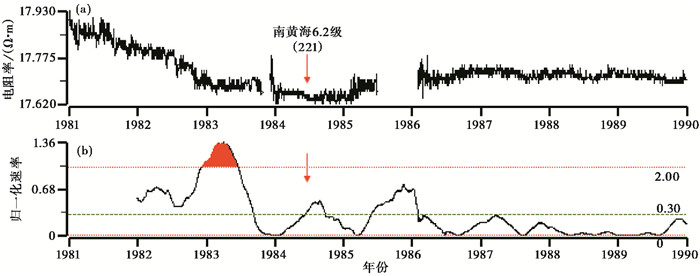
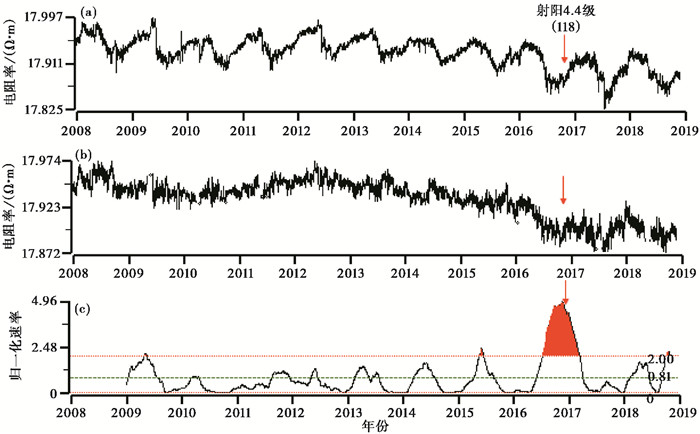
图 5显示1990年年底至1991年年底出现趋势下降变化, 最大相对变化幅度约为0.99%, 之后1991年11月5日在射阳发生4.7级地震, 地震后数据变化平缓, 直到1995年年中再次出现快速上升变化趋势, 之后1996年11月9日在南黄海发生6.1级地震, 震前趋势变化相对幅度约为1.4%。从归一化速率曲线来看, 这2次趋势变化速率均超过2倍均方差, 最大归一化速率值分别为2.8和3.1。图 6为2010~2018年海安台新场地SN向地电阻率日值和归一化速率曲线, 图中显示2010年以来观测数据存在长期的趋势下降变化, 在下降过程中发生了2012年7月20日高邮-宝应4.9级地震, 从归一化速率曲线来看, 2011年9月底出现高值, 超过2倍均方差, 最大归一化速率值为2.9。图 7为1981~1989年高邮台旧场地EW向地电阻率日值曲线, 图中显示1981年以来观测数据存在长期的趋势下降变化, 在下降的底部区域发生了1984年5月21日南黄海6.2级地震, 趋势下降最大幅度约为1.1%, 从归一化速率曲线来看, 趋势变化速率超过2倍均方差, 最大归一化速率值为1.4。图 8为2008~2018年高邮台新场地EW向地电阻率日值曲线, 图中显示2014年后观测数据的趋势下降变化明显, 在下降的底部区域发生了2016年10月20日射阳4.4级地震, 趋势下降最大幅度约为0.31%, 从归一化速率曲线来看, 趋势变化速率超过2倍均方差, 最大归一化速率值为4.9。

根据图 4~图 8的分析, 地电阻率观测数据出现明显的趋势变化, 在趋势变化结束或转折后, 周围容易发生显著地震。考虑到各观测场地的电性结构不一致, 一般很难定义趋势变化幅度的异常量, 采用365天的归一化速率处理后, 从实际的检验效果来看, 采用2倍方差定义指标是合理的。

2.4 预测检验

根据以上分析, 采用365天归一化速率计算对两类异常现象建立统一的预测指标：超过5年的连续观测数据中, 归一化速率超过2倍方差判断为异常。根据这一规则, 对江苏所有观测场地进行了扫描(去除观测不超过5年的场地和干扰明显的数据, 如新沂台的SN向长期受蔬菜大棚干扰, 南京台高淳基地的铁塔干扰等), 同一场地的不同方向测道同时出现异常时, 只采用1个方向的异常, 一共得到了11次异常。6级及以上地震对应空间为台站周围300km, 5~6级地震对应空间为台站周围250km, 4.4~5级地震对应空间为台站周围200km, 结合表 1, 得到表 2。表 2显示每个场地的异常变化幅度差别较大, 但同一场地年变化幅度和归一化年速率值越大, 对应的震级越大, 采用归一化年速率值的预测时间均在12个月之内, 11次异常的对应率为10/11, 如果预测时间采用9个月, 对应率为9/11, 同时存在5级及以下地震的漏报情况, 漏报地震7个。

R值检验有多种计算方法, 王晓青(2000)对R值计算方法进行了讨论。采用如下计算公式(国家地震局科技监测司, 1990)

$ R = \frac{{报对的地震次数}}{{预测范围内发生地震总次数}} - \frac{{预测占用时间}}{{预测研究的总时间}} $

(7)

式(7)的第一部分考虑了漏报问题, 第二部分考虑了虚报问题。考虑到涉及多个台站观测场地, 因此把所有场地的报对次数、应报次数、预测占用时间、预测研究总时间均进行求和计算(同一场地多次预测, 研究总时间不累加, 只累加预测时间)。根据表 2, 给出的有效预测时间取最大为9个月(去掉预测时间为12个月的), 虚报的预测时间均取9个月, 得到报对次数9次, 应报地震数16个, 预报占用时间64个月, 预测研究的总时间为1320个月。代入式(7), 得出$R = \frac{9}{{16}} - \frac{{64}}{{1320}} = 0.513$，以上R值计算具有97.5%置信率, 对应R₀为0.277, R/R₀=1.9, 因此, 可以认为预测是比较有效的, 给出的预测指标是合理的。

2.5 预测指标

根据以上的计算分析结果, 给出江苏地区地电阻率的预测指标。基本算法为：5年以上连续观测数据先进行傅氏拟合去年变, 采用365天窗长计算归一化速率；异常判据指标：归一化速率值2倍方差以上；预测规则：归一化速率值达到最大异常后, 9个月以内, 台站周围200km、250km、300km存在分别发生4.4~5级、5~6级、6级及以上地震的可能, 归一化速率值越大, 震级越高。

3 讨论

(1) 岩石实验和实际观测均表明, 具有前兆性质的地电阻率异常变化与岩石裂隙变化有关。在岩石裂隙变化的线性阶段, 一般地电阻率的变化也接近线性, 表现为趋势向上或向下；在岩石裂隙的扩容扩散阶段, 一般地电阻率的变化为非线性的下降变化或破年变变化。两类异常变化在实际观测中均具有一定的预测意义, 但由于观测场地的参数、地下电性结构等不同, 即使采用相对变化, 一般很难通过原始数据给出相对统一的预测指标。鉴于此, Du等(2001)给出了归一化月速率判定方法, 并给出了归一化速率值为2.4的判定指标。在实际的观测中, 由于短期的降雨等影响, 很多场地的观测数据的年变不是非常规则, 数据分析也较难将年变处理干净, 采用月速率法处理时发现引入干扰的情况较多, 而从两类异常来看, 异常的形成时间一般比较长, 因此本文采用了一年窗长的归一化速率判定方法；此外, 考虑到不同的观测场地对计算归一化速率值的影响, 采用2倍方差作为异常判定指标, 表 2中给出的归一化速率值基本都在2.5以上, 与Du等(2001)给出的异常数值较一致。

(2) 根据实际观测结果完成预测指标和预测检验存在很多问题, 一是由于观测台址条件和环境的不同, 不同观测场地的异常形态和幅度可能会存在较大差异, 因此一般很难给出一个学科或方法的统一预测指标, 而采用以单台观测数据建立的预测指标, 一般存在观测数据连续性、对应地震样本数等问题而无法作出合理的预测检验。另外, 单学科或方法给出的预测指标存在很多局限性, 预测三要素中往往只能给出1~2个要素, 一般给出的预测指标得到的R值检验结果大多并不理想, 因此如何综合各学科或方法建立预测指标, 并更多地从物理机制出发给出预测三要素的判定指标是值得探讨和思考的