τc方法在内蒙古地区预警震级计算中的应用
郝美仙, 周银兴, 张建中, 张珂, 尹战军
中国地震  2020, Vol. 36 2020, Vol. 36 Issue (1): 136-145 Issue (1): 136-145
|
地震预警是减轻地震灾害的有效手段之一, 该技术已被国际上越来越多的国家和地区所重视, 相应地建立了各自的地震预警系统, 并在实际应用中取得了较为明显的减灾效果(Allen et al,2003;Wu, 2005;Bose et al,2009)。其基本原理是利用部署在潜在震源区周围的实时传输地震观测台站, 在破坏性地震发生后的极短时间内, 根据距离震中较近的若干个触发台站的信息, 迅速测定地震发生的地点和规模, 并利用地震波P波传播速度大于更具破坏性的S波和面波传播速度的特点和地震波传播速度远远小于电磁波的原理, 在破坏性地震动到达之前向周围可能遭受地震影响的地区发出警报(马强, 2008)。
随着我国经济的快速发展和城市化进程的加快, 核电站、大型石化工程等重大基础设施不断涌现, 高速铁路、长输管线、城市管网等生命线工程日趋密集、复杂。重大基础设施和生命线工程一旦遭遇破坏性地震, 在遭受直接灾害的同时, 还会导致更为严重的次生灾害, 造成重大的社会影响。如何减轻地震灾害、最大限度地降低地震造成的人员伤亡和经济损失, 是政府和全社会极为关注的课题。地震预警系统可以在检测到破坏性地震发生时, 自动启动城市及重大工程地震紧急处置系统, 快速地向相关行业及公众提供预警信息, 切实地减轻地震灾害。《国家中长期科学和技术发展规划纲要(2006~2020年)》 ①中明确提出要“重点研究开发地震、台风、暴雨、洪水、地质灾害等监测、预警和应急处理关键技术, 森林火灾、溃坝、决堤险情等重大灾害的监测预警技术以及重大自然灾害综合风险分析评估技术”;陈颙(2004)在《2020年中国地震科学和技术发展研究》中更是明确提出了要建设地震灾害预警平台。目前, 我国正在开展建设的国家地震烈度速报与预警工程的关键核心任务之一就是建设覆盖全国范围的地震预警系统。
① http://www.most.gov.cn/mostinfo/xinxifenlei/gjkjgh/200811/t20081129_65774_6.htm
但是, 地震预警系统中存在着一个关键的难题, 就是如何从一个正在发生的地震事件中估算出震级大小(金星等, 2012a)。由于计算预警震级时往往只有附近少数触发台站的有限时间长度内的信息可以利用, 因此不可能采用常规震级算法进行计算。同时,地震预警系统还要求所发布的信息具有足够可靠性, 因此必须发展一些非常规的、稳定可靠的实时震级计算方法(金星等, 2012a)。
目前国际上已发展了一些实用的实时震级计算方法, 根据方法的特点大致可分为三类(张红才等, 2012):与周期或频率相关的算法、与幅值相关的算法以及与辐射能量强度相关的算法。我国学者也针对其开展了一定的研究,金星等(2012b)利用日本KiK-net台网数据和四川汶川地震余震序列获取到了特征周期τc和位移幅值Pd与震级的相关性, 并将其应用到福建研发的地震预警系统中;彭朝勇等(2013)使用2008年汶川地震序列强震动观测数据来研究适用于四川地区的预警参数与最终震级大小之间的相关性, 为建立适用于四川地区的地震预警系统提供参考。从上述研究结果可以看出, 预警震级估算方法有其地域特点。因此, 在建设地震预警系统时, 需要首先利用本地的数据重新构建地震预警系统震级估算模型, 并对其开展分析研究, 以进一步提高预警震级的可靠性。
本文使用内蒙古地区测震台站记录到的地震事件数据, 来研究适用于本区域的τc值与预警震级之间的相关性, 为“十三五”国家地震烈度速报与预警工程在我区的实际应用提供技术支撑。
1 τc方法简介Nakamura(1988)提出P波卓越周期(τp), 即利用实时速度记录计算地震动卓越周期的算法。多位学者(Allen et al,2003;Kanamori, 2005;Olson et al,2005)采用该方法进行了一系列相关研究, 其计算公式如下
| $ {\tau _{{\rm{p}}i}} = 2{\rm{ \mathit{ π} }}\sqrt {\frac{{{X_i}}}{{{Y_i}}}} $ | (1) |
式中,
针对τp方法的局限性, Kanamori(2005)提出另外一种改进后的P波特征周期计算方法, 即τc方法, 其计算公式如下
| $ {\tau _c} = 2\pi \sqrt {\frac{{\int_0^{{t_0}} {{u^2}} (t){\rm{d}}t}}{{\int_0^{{t_0}} {{{\dot u}^2}} (t){\rm{d}}t}}} $ | (2) |
式中, 积分区间[0, t0]从台站触发开始计时, t0的单位为s, u(t)代表高通滤波后垂直分向地震动位移值。时间窗长度t0的选择直接关系到预警信息发布的时间, 如果t0选择太长, 预警信息发布的时间就会变短;如果t0选择太短, 则不能对地震规模进行准确的估算。Kanamori(2005)结合各种因素综合考虑, 建议一般情况下t0取值为3s。在实际应用中, 不同学者对τc方法计算震级有各自的研究结果。Wu(2005)通过研究得出, 在该段时间内, 可以利用τc参数较为准确地估算地震的大小, 对其是否具有破坏性能够作出快速的判断。
运用巴什瓦(Parseval)定律对式(2)进一步分析表明,得出的τc就是位移谱重心位置处的周期。采用中小地震的Brune震源模型可以证明, 计算得出的周期参数τc其实就是P波的拐角频率;对于破坏性较大的地震, τc是确定地震大小的有效参数。因此, 本文采用τc方法进行计算。
2 数据选取和预处理张红才等(2012)在地震预警震级计算方法研究中得出, τc方法更适用于我国台网建设的现状, 即使使用单个台站的波形数据也能得到比较稳定的震级估算值, 推荐该方法作为我国地震预警系统中优先采用的震级算法之一。根据内蒙古测震台网台站间距较大、单个地震事件记录台站较少的实际情况, 本文对震级估算仅采用τc方法进行研究。
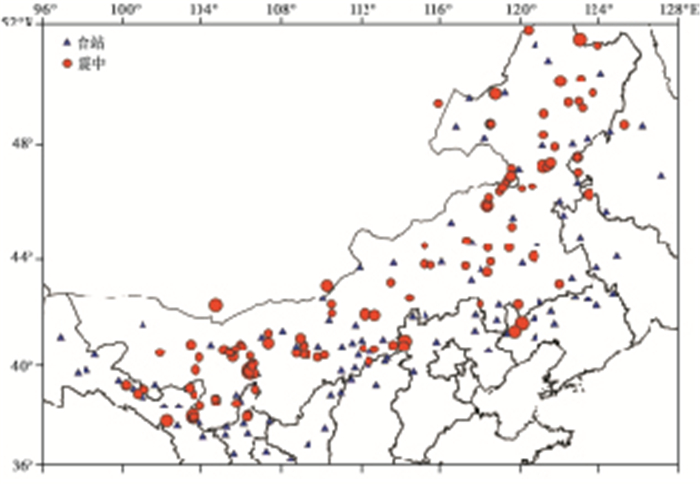
本文采用内蒙古测震台网地震波形数据, 选取时间范围为2016~2018年, 因内蒙古地区发生的较大地震较少, 故选取ML≥2.0地震波形数据(Kuyuk et al,2013), 共120条。本研究所测定的震级标度为ML。所选地震事件和台站分布如图 1所示, 所用事件和记录情况统计如图 2所示。
|
图 1 本文选取地震事件与台站分布 |
|
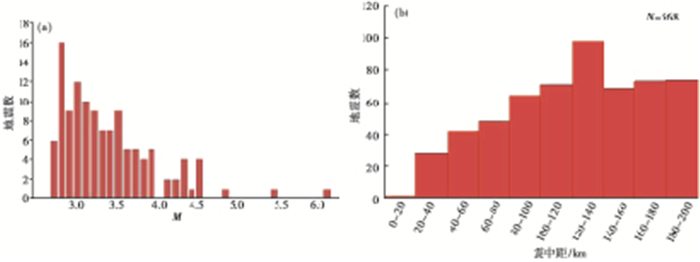
图 2 本文所用事件和记录情况统计 (a)所用事件的震级情况;(b)所用记录的震中距情况 N为记录事件个数 |
因地震发生的成因很复杂, 对于同一个地震的不同台站的波形记录, 所提取的特征参数不尽相同。但对同一个地震事件取多个台站的观测结果, 用平均值进行相关研究, 震级统计结果将更具有可靠性。鉴于目前内蒙古台网现状, 我们选择了震中距在200km以内的台站记录参与分析计算。实际上地震预警需要更密集的观测网。
对于筛选得到的各台站事件记录数据, 首先通过手动方式选取P波和S波到时, 然后对台站垂直向的速度记录和加速度记录分别进行一次积分和二次积分, 以获取位移时程, 并对位移时程进行连续巴特沃斯(Butterworth)高通滤波器滤波处理(截至频率0.075Hz),以移除由于积分操作带来的低频漂移影响。前人研究结果显示, 在对数据进行滤波处理时, 利用较多的滤波器极点数目可以有效地压制τc值的发散性, 从而提高震级估算结果的准确度。考虑到我国的测震观测数据相对于国外数据质量较差, 而τc参数对数据质量要求较高, 因此, 本文在对数据进行预处理时采用的是含有4个极点的巴特沃斯高通滤波器, 而不是通常使用的只含有2个极点的巴特沃斯高通滤波器。最后, 根据P波后3s时间窗内垂直向位移时程和P波全波段(P波到达后至S波之间)垂直向位移时程, 计算周期参数τc值。
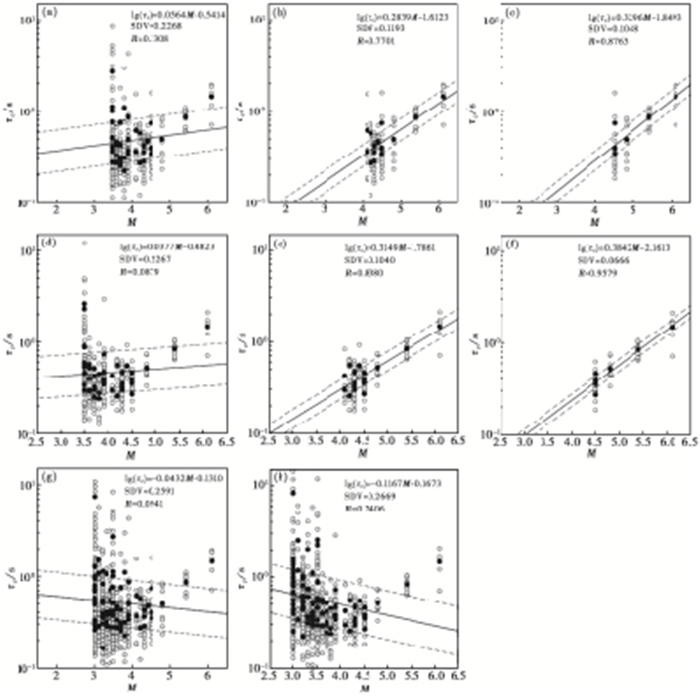
3 τc方法计算结果本研究基于选取的内蒙古测震台网记录的地震事件波形, 采用P波后3s时间窗内垂直向位移时程和P波全波段垂直向位移时程, 分别按照不同梯度的地震震级进行计算, 具体为M≥3.0、M≥3.5、M≥4.0和M≥4.5四个震级标度区间计算τc值, 再采用M=a+blg(τc)拟合, 分别得到了不同震级段P波3s内和P波全波段特征周期与震级之间的关系, 拟合结果如图 3所示。实际应用时推荐采用M≥4.5的拟合公式, 同时加上其他预警参数或地震动参数阈值判定, 以避免由于小震震级估高带来的误报问题。
|
图 3 特征周期τc与震级在时窗P波后3s(a)、(b)、(c)、(g)和P波全波段(d)、(e)、(f)、(h)的相关关系 圆点表示每条台站记录的τc值;黑色实线表示线性拟合曲线;黑色虚线表示1倍标准方差;实心圆为一次地震各个台站τc值的均值;空心圆为每个台站计算得到的τc值 |
图 3(a)~3(c)为分别采用P波后3s时间窗内按照不同震级计算得出的τc值与震级之间的拟合关系式。实际结果完全符合使用的一般规律:“小报大, 大报小, 不大不小还好”, 即用P波前几秒处理地震震级往往是小地震时会偏大, 大地震时会偏小, 而中等地震还比较接近。当然这里指的是地震预警的最快的警报, 也就是第一报, 这其实是地震预警的技术局限性之一。后续的警报会越来越准确, 但是这样发出去的警报将会使预警盲区越来越大, 接收警报的人就越来越少, 地震预警减少灾害的效能越来越小。图 3(d)~3(f)分别为采用P波全波段时按照不同震级计算得出的τc值与震级之间的拟合关系式。从图 3的结果可以看出, 根据斜率、SDV(标准偏差)及R(相关系数)参数的对比, 随着震级下限的增大, 斜率随之增大。利用M≥4.0地震拟合时, 上述3个参数的3条线斜率基本是一定的, 周期参数τc能较好地反映地震规模, 且采用P波全波段计算得到的τc值统计关系的离散性明显优于采用窗长3s的计算结果。此外, 图 3(h)、3(i)分别为M≥3.0地震采用P波后3s时间窗和P波全波段计算得出的τc值与震级之间的拟合关系式, 从图 3可以看出, 2.0≤M<3.5地震由于记录数据的信噪比较低, 再加上小地震频谱复杂程度比大地震高, 使得计算获得的τc值变化范围过大。
特征周期τc对于信噪比的要求较高, 通常来说小地震频谱较高, 但是小地震的频谱复杂程度要比大地震高, 也就是说, 如果地震波传输路径带有非线性介质, 是可能产出多种频率成分的, 因此使用τc法往往会使小震误报为大震, 因此较小的地震事件(如M<4.0)不适宜采用该方法估计预警震级。
4 数据实际应用分析为了将本文的研究结果应用到实际中, 选取文中统计震例范围外的2次地震事件开展震级估算线下模拟, 分别为2017年6月3日18时11分内蒙古阿拉善左旗ML5.4地震和2016年6月23日08时37分河北尚义ML4.5地震, 分别按照M≥4.0、M≥4.5全波段值和窗长3s的P波段信息拟合的特征周期τc与地震震级间的关系式, 对地震震级进行计算
| $ \begin{array}{*{20}{l}} {lg\left( {{\tau _c}} \right){\rm{ = }}0.3149M{\kern 1pt} - {\kern 1pt} {\kern 1pt} } \end{array}1.7861 $ | (3) |
| $ \begin{array}{*{20}{l}} {lg\left( {{\tau _c}} \right){\rm{ = }}0.2839M - {\kern 1pt} {\kern 1pt} } \end{array}1.6123 $ | (4) |
| $ \begin{array}{*{20}{l}} {lg\left( {{\tau _c}} \right){\rm{ = }}0.3842M{\kern 1pt} - {\kern 1pt} {\kern 1pt} } \end{array}2.1613 $ | (5) |
| $ \begin{array}{*{20}{l}} {lg\left( {{\tau _c}} \right){\rm{ = }}0.3296M - {\kern 1pt} {\kern 1pt} } \end{array}1.8493 $ | (6) |
M≥4.0地震P波全波段与P波后窗长3s特征周期τc与震级统计如式(3)、(4)所示, M≥4.5地震P波全波段与P波后窗长3s特征周期τc与震级统计如式(5)、(6)所示。
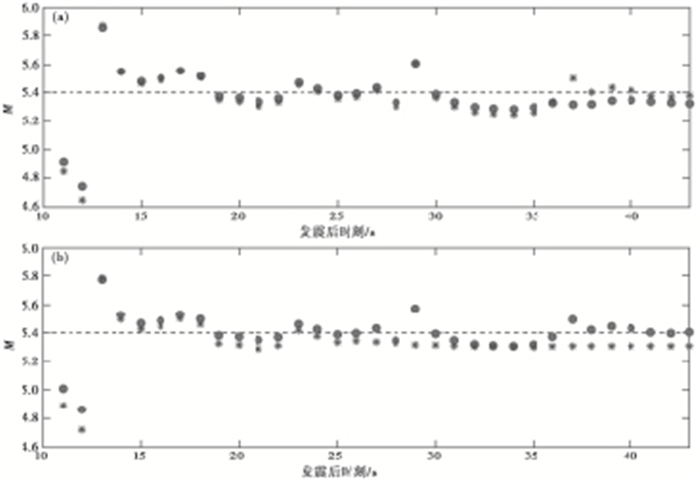
图 4(a)、5(a)为利用式(3)、(4)计算的震级值, 图 4(b)、5(b)为利用式(5)、(6)计算的震级值。结果显示, 采用P波全波段值拟合τc与地震震级间的关系式计算得出的震级, 震级离散型更小, 明显优于采用窗长3s的P波段拟合关系式得出的震级值。但由于现有内蒙古测震台网台间距过大, 超过150km, 导致在对地震震级进行估算时, 需要较长的时间。
|
图 4 内蒙古阿拉善左旗ML5.4地震震级拟合图 (a)按照M≥4.0地震拟合公式得出;(b)按照M≥4.5地震拟合公式得出实点为P波全波段τc拟合;*为P波后3sτc拟合 |
|
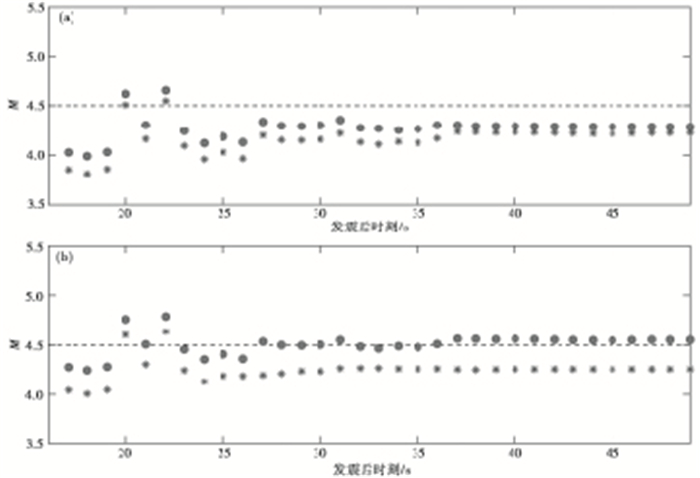
图 5 河北尚义ML4.5地震震级拟合图 (a)按照M≥4.0地震拟合公式得出;(b)按照M≥4.5地震拟合公式得出实点为P波全波段τc拟合;*为P波后3sτc拟合 |
此外, 利用M≥4.5地震拟合关系式得出的震级值, 更接近所选地震的最终编目震级, 且震级总体变化趋势更为集中, 偏差较小。
利用本文的全P波τc方法, 对于5级左右地震, 在P波到达20s后即可接近实际地震震级, 这对于快速测定地震震级具有实际应用价值。同时, 对于地震预警, 在3s之内的测定的震级仍然有较大误差, 这符合上述的结论, 而这个问题从地震观测原理来说, 是由于3s内P波并不能代表地震释放的全部能量, 所以用它来快速测定地震震级, 会带来误差, 这也恰恰是地震预警技术需要改进和突破的瓶颈。在目前这种情况下, 地震预警技术发布策略也是需要引起注意的问题。
5 讨论与结论本文根据内蒙古测震台网地震目录, 选取了内蒙古测震台网满足一定筛选条件的波形记录, 对所选记录进行人工识别P波和S波震相, 之后对P波后3s时间窗内和P波全波段的垂直向位移时程进行τc值计算, 得出在M≥3.0、M≥3.5、M≥4.0和M≥4.5时, P波3s时间窗和P波全波段的τc值与地震震级之间的关系。统计结果显示, 随着计算τc值时选取震级的增大, 拟合结果直线的斜率也随之增加。因为τc方法对数据噪声要求比较高, 因此, 当采用M≥3.0、M≥3.5地震事件记录时, 拟合曲线斜率很小, 使得该参数失去了实时震级估算的意义。当采用M≥4.0事件记录计算时, τc值更为收敛, P波全波段的τc值较P波3s时间窗计算值收敛性更好, 拟合相关系数更接近1。由于本文没有7级以上地震的实例, 因此无法用此方法对大地震进行震级计算的验证。尽管如此, 我们获得了大量实际观测和计算的宝贵数据, 综合研究表明:
(1) 特征周期τc能够对预警地震震级作出较好的估计, P波全波段的τc值较P波3s时间窗计算值收敛性更好。实验表明P波全波段τc方法对于5级左右地震, 在P波到达20s以后即可接近实际地震震级, 但较小的地震事件(如M<4.0)不适宜采用该方法估计预警震级,这对于快速测定地震震级具有实际应用价值, 可以大大提高区域地震台网地震速报的速度。但是, 本研究表明, 利用τc方法无法在地震预警要求的极短时间内(例如3s)测量计算出较准确的震级, 也就是说, 这个方法在地震到达台站15~20s之内测量震级的误差还是比较大的。这个现象还表明, 地震P波前3s或者P波全波段的信息还无法代表整个地震能量释放的信息, 因此无法代表地震准确的震级。在这种情况下, 最初发出的地震预警信息中地震震级误差较大是必然的, 这个问题就是我们常说的目前地震预警技术的局限, 也是地震预警技术在震级快速测定上需要不断改进之处。
(2) 对于地震预警,即使理想状态下可以很快地测算出准确的地震参数, 也很难预估出警报接收地的震动强度, 这里同样受到地震破裂过程、地震波传播特性、警报接收地当地场地效应等诸多因素的影响。因此, 地震预警的警报发布需要根据目前地震震级测定水平及地震预警接收地的地震烈度估计水平等复杂的情况,确定警报发布的策略和方式。单一的周期参数在一定程度上能够反映地震的规模, 但不能反映地震的全部特征。因此, 预警震级的估算应结合多个参数综合判定。
(3) 由于内蒙古自治区内台站少、分布广, 目前平均台间距超过150km, 导致在较小地震发生后, 大部分台站记录的信噪比较低, 使得利用P波特征周期计算预警震级的稳定性和可靠性受到限制, 预警盲区较大。但是, 随着国家地震烈度速报与预警工程的建立, 台网密度将会大大增加,盲区的范围将大大缩小, 对预警震级的准确测定会有极大的提升。
只有密集的地震预警网才能发挥地震预警的效益, 一般认为地震预警网的台站密度应为台间距10km, 这需要大量采用低成本的MEMS传感器。尽管如此, 对于内蒙古地区应该根据实际情况来布设的, 对于人口稠密的地区和大中城市, 应该布设密集的地震预警台网, 当然, 对于高烈度区域或者具有发生大地震的危险区域, 也需要布设密集地震预警网, 一方面, 对于该地区发生大地震可以快速预警, 另一方面, 也是对远处人口稠密地区的守备式地震预警。对于人口稀少和无人地区则无需密集的地震预警网。
(4) 综上所述, 地震预警技术在实际应用中, 存在对地震震级快速测定的不确定性, 通常是“小报大, 大报小, 不大不小还好”及“快就不准”, 这必定影响地震预警参数计算的不确定性, 导致在指定对应的阈值时会出现较大的偏差。Minson等(2018、2019)指出在使用较低的预警参数阈值时, 目前采用以快速发出警报优先的策略, 对于经过有效训练的公众来说, 虽然收到的误报事件会很多, 但是却能将预警效能最大化, 因为公众在收到预警信息后所采取的动作(如蹲下、掩护、抓紧)的成本投入非常低。对于内蒙古地区而言, 在实际部署和运行地震预警系统时, 也可以采用类似的方法, 以便有效提高预警系统的效能。对于其处理策略和方法, 今后还需进一步开展研究。
本文主要针对内蒙古地区开展预警参数关系式研究, 采用的全P波段的方法也是Peng等(2017)所采用的一种新方法。这种方法只是在做拟合关系时的应用, 实际在做线下模拟和应用至地震预警系统时, 采用的仍然是P波触发后第一秒数据就开始持续应用的模式, 一直到S波截止, 不同的是采用新的拟合关系式进行震级估算。由于缺乏M≥ 7.0大地震的实例检测, 本文的研究结果仅限于中强以下地震。
致谢: 感谢彭朝勇研究员在本文撰写过程中给予的指导, 感谢审稿专家对本文提出的宝贵修改意见。
陈颙, 2004. 2020年中国地震科学和技术发展研究.见: 2020年中国科学和技术发展研究暨科学家讨论会论文集(下册).北京: 中国科学技术协会.
|
金星、张红才、李军等, 2012a, 地震预警连续定位方法研究, 地球物理学报, 55(3): 925-936. |
金星、张红才、李军等, 2012b, 地震预警震级确定方法研究, 地震学报, 34(5): 593-610. |
马强, 2008.地震预警技术研究及应用.博士学位论文.哈尔滨: 中国地震局工程力学研究所. http://d.wanfangdata.com.cn/Thesis/Y1597107
|
彭朝勇、杨建思、薛兵等, 2013, 基于汶川主震及余震的预警参数与震级相关性研究, 地球物理学报, 56(10): 3404-3415. DOI:10.6038/cjg20131016 |
张红才、金星、李军等, 2012, 地震预警震级计算方法研究综述, 地球物理学进展, 27(2): 464-474. DOI:10.6038/j.issn.1004-2903.2012.02.009 |
Allen R M, Kanamori H, 2003, The potential for earthquake early warning in southern California, Science, 300(5620): 786-789. DOI:10.1126/science.1080912 |
Bose M, Hauksson E, Solanki K, et al, 2009, A new trigger criterion for improved real-time performance of onsite earthquake early warning in southern California, Bull Seismol Soc Am, 99(2A): 897-905. DOI:10.1785/0120080034 |
Kanamori H, 2005, Real-time seismology and earthquake damage mitigation, Annu Rev Earth Planet Sci, 33: 195-214. DOI:10.1146/annurev.earth.33.092203.122626 |
Kuyuk H S, Allen R M, 2013, A global approach to provide magnitude estimates for earthquake early warning alerts, Geophys Res Lett, 40(24): 6329-6333. DOI:10.1002/2013GL058580 |
Minson S E, Baltay A S, Cochran E S, et al, 2019, The Limits of earthquake early warning Accuracy and Best Alerting strategy, Sci Rep, 9(1): 2478. |
Minson S E, Meier M A, Baltay A S, et al, 2018, The limits of earthquake early warning:Timeliness of ground motion estimates, Sci Adv, 4(3): eaaq0504. DOI:10.1126/sciadv.aaq0504 |
Nakamura Y, 1988. On the Urgent Earthquake Detection and Alarm System(UrEDAS). In: Proceedings of Ninth World Conference on Earthquake Engineering. Tokyo-Kyoto: 9WCEE Organizing Committee, 673~678.
|
Olson E L, Allen R M, 2005, The deterministic nature of earthquake rupture, Nature, 438(7065): 212-215. DOI:10.1038/nature04214 |
Wolfe C J, 2006, On the properties of predominant-period estimators for earthquake early warning, Bull Seismol Soc Am, 96(5): 1961-1965. DOI:10.1785/0120060017 |
Wu Y M, 2005, Rapid assessment of damage potential of earthquakes in Taiwan from the Beginning of P Waves, Bull Seismol Soc Am, 95(3): 1181-1185. DOI:10.1785/0120040193 |
Peng C Y, Yang J S, Zheng Y, et al, 2017, New τc regression relationship derived from all P wave time windows for rapid magnitude estimation, Geophys Res Lett, 44(4): 1724-1731. |