2. 中国科学院大学, 地球与行星科学学院, 北京 100049;
3. 福建农林大学, 交通与土木工程学院, 福州 350002;
4. 中国地震台网中心, 北京 100045
2. College of Earth and Planetary Sciences, University of Chinese Academy of Sciences, Beijing 100049, China;
3. College of Transportation and Civil Engineering, Fujian Agriculture and Forestry University, Fuzhou 350002, China;
4. China Earthquake Networks Center, Beijing 100045, China
板块边界带附近的应力场主要由两部分构成,即一阶应力场和二阶应力场。其中,一阶应力场是由与板块运动的动力驱动机制直接相关的力产生的,比如洋脊推力、板片拉力、大陆碰撞力等,其水平尺度往往超过1000km,构成某一地区的背景应力场。而二阶应力场主要是由与局部构造直接相关的力产生的,比如局部岩石层的挠曲,局部横向密度差异、横向岩石强度差异等,其水平尺度为100~200km,叠加在大尺度应力场上,反映了局部的地质构造特征(Zoback,1992;黄玺英等,2003、2004;Wan,2010)。岩石层中的应力主要来源于板块的构造运动,板块运动驱动力的大小决定着岩石层应力的强度,而岩石层的应力状态又决定着构造变形的特征以及板块边界和板块内部的地震活动(谢富仁等,2003)。在俯冲带地区,其构造应力场的特征十分复杂,板块水平运动的大洋板块推力、导致板块重力下沉的大洋板块拉力、海沟附近的断层闭锁和板块俯冲的负浮力等共同制约着俯冲带内的应力场(高祥林等,1994)。俯冲板块内部的应力状态随着区域变化而变化,且同一俯冲板片内的应力状态在沿着俯冲方向及其垂向上均存在变化(张克亮等,2008)。不同俯冲带内应力状态随地理位置、俯冲深度的不同而存在差异,且有些俯冲地区呈现非平行俯冲方向的应力状态(孙振添等,2013)。
地震震源机制是反映地球深部应力状态的主要参数,资料来源最为广泛,因此,基于震源机制解来研究深部构造应力场成为主流方法之一(许忠淮等,1983、1989;郑建常等,2013;Gephart et al,1984;Matsumoto et al,2015;Yoshida et al,2016;Xu et al,2016;Konstantinou et al,2017;Wu et al,2017;)。随着构造应力反演技术的逐步完善,利用地震资料反演俯冲带应力场,成为俯冲带动力学研究的热点问题。Wada等(2010)通过震源机制解反演得到了卡斯卡地亚俯冲带的俯冲板片内部的应力场状态。Kumar等(2016)利用震源机制解研究了秘鲁中部、南部贝尼奥夫带以及纳兹卡板块俯冲板片的应力状态。Christova研究小组利用Gephart等(1984)提出的FMSIA方法反演了北海道贝尼奥夫带(Christova et al,2000)、勘察加半岛贝尼奥夫带(Christova,2001)、瓦努阿图(Christova et al,2003)、琉球群岛-九州俯冲带(Christova,2004)、伊豆-小笠原(Christova,2005)、千岛群岛贝尼奥夫带(Christova,2015)等地区的构造应力场特征。Meighan等(2013)采用阻尼张量反演方法,发现波多黎各海沟存在板片撕裂现象。黄骥超等(2016)基于Global CMT目录,利用网格搜索法对汤加-克马德克俯冲带区域进行应力张量反演,得到研究区域内精细的应力场图像,证实了地幔流导致应力场偏转,还发现主俯冲带深部西侧“偏移”板片与主俯冲带是分离的。崔华伟等(2019)利用阻尼应力张量反演方法,得到了帕米尔-兴都库什地区构造应力场图像。杨佳佳等(2018)基于NIED F-net矩张量解目录中的震源机制解,采用阻尼应力张量反演方法得到日本海沟俯冲带MW9.0地震震源区应力场图像。李天觉等(2019)基于Global CMT提供的地震矩心矩张量解,对西北太平洋俯冲带日本本州至中国东北段的应力场进行反演,得到了从浅表到深部俯冲带应力状态的完整分布图像。
已有的俯冲带应力场研究成果(Christova,2001、2004、2005、2015;黄骥超等,2016;李天觉等,2019)丰富了我们对俯冲过程中俯冲板片的形态及俯冲带内部应力状态的认识。但是,对于鄂霍次克微板块东部边界的日本地区、千岛地区和勘察加地区的俯冲带应力场特征,目前仍缺乏更加细致的对比研究。因此,本文对鄂霍次克微板块东部俯冲带区域内的地震资料进行构造应力场反演,对上述3个地区(日本地区、千岛地区和勘察加地区)俯冲带不同深度区域的应力场图像进行细致描绘,并分析其各自应力场分布的异同点。研究结果有助于更加清晰地了解板块边界处的地球动力学过程及其二阶应力场分布特征,并可帮助我们认识板块内部的应力场产生机制和该板块的运动驱动机制。
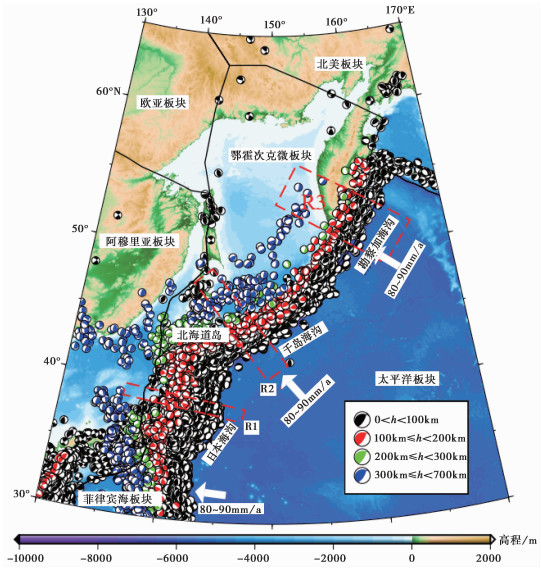
1 区域构造环境概况西北太平洋俯冲带地震频发,是全球最活跃的俯冲带之一。太平洋板块、菲律宾海板块、欧亚板块以及北美板块等在此相互作用,以俯冲为主兼有走滑运动,从而影响各个相关板块边缘及板块内部的动力过程、应力场特征和构造运动(臧绍先等,1996)。鄂霍次克微板块自北美板块独立出来,楔形插入欧亚板块和太平洋板块之间,南部与菲律宾海板块相接,东部边界受到太平洋板块的强烈俯冲作用,地震活动频繁发生(Seno et al,1996;DeMets et al,2010)(图 1)。在鄂霍次克微板块东部边界,俯冲带的几何形态特征自北向南有所变化,勘察加海沟地区的俯冲角度为55°(Levin et al,2002)。千岛群岛分布在环太平洋西岸45°N至53°N之间,太平洋板块以每年80~90mm的速率向千岛群岛下俯冲了65~85Ma,是环太平洋板块俯冲发生较早的地区之一(何建坤等,1998)。由于太平洋板块俯冲,在千岛群岛岛弧西侧发育了拉伸成因的且现已由大洋地壳和过渡性地壳构成的鄂霍次克边缘海(何建坤等,1998)。在鄂霍次克海南部区域,存在因俯冲作用导致弧后扩张形成的千岛海盆,目前依然处于扩张阶段(任建业等,2000)。千岛群岛和达-贝尼奥夫带(Wadati-Benioff)比较规则,呈NE走向,俯冲带倾向310°,俯冲倾角由东北端的47°向西南减缓至31°,平均俯冲倾角为45°;北海道岛浅源地震呈NEE走向,俯冲带倾向322°,俯冲倾角36°,北海道岛及其附近地区受日本海俯冲带向西强烈俯冲影响,浅源地震分布走向变化较大,由千岛群岛的NE向到该区转为近EW向(孙文斌等,2004);日本海沟地区和达-贝尼奥夫带(Wadati-Benioff)较平直,走向近SN,俯冲带倾向283°,平均俯冲倾角29°(孙文斌等,2004)。
|
图 1 鄂霍次克微板块及其附近地区震源机制解分布(据Seno等(1996)) 地形图根据ETOPO1高程数据绘制①;白色箭头表示太平洋板块俯冲方向;黑色实线为板块边界 |
① https://www.ngdc.noaa.gov/mgg/global/global.html
2 方法和数据 2.1 方法根据地震资料的震源机制解获取某一地区的应力场分布,主要有2种方法。一种方法直接对该地区内的所有地震震源机制解进行统计分析,每个地震震源机制解均给出了其主压应力轴(P轴)、中间应力轴(B轴)和主张应力轴(T轴)的走向、倾伏角等信息,对P轴、T轴方位信息进行归纳分类,多个地震震源机制解的平均P轴、T轴方位与震源区实际应力主轴方位近似(宁杰远等,1987;吴忠良等,1989;徐纪人等,2003、2008)。另一种方法是基于多个地震震源机制解来反演该区域的应力张量,目前成熟的法向应力反演技术主要基于2个假设:①研究区域地壳范围内应力场是均匀的;②断层的滑动方向与应力张量投影在断层面上的剪切应力方向一致(Wallace,1951;Bott,1959)。估计应力场方向和相对大小是非线性求解问题,既可以直接求解,也可采用线性化求解(王晓山等,2015)。前人提出的应力场反演的网格搜索法(Gephart et al,1984;Wan et al,2016)和基于采样优化的蒙特卡洛方法(Angelier,1984;Xu,2004)均属于非线性求解。目前被广泛应用的最小二乘法是线性反演方法(Michael,1984;Hardebeck et al,2006)。Hardebeck等(2006)开发了SATSI软件,采用阻尼最小二乘反演得到各网格格点的应力张量并进行平滑处理。
本研究所使用的MSATSI软件是在SATSI软件基础上进一步完善的MATLAB应力反演程序包(Martínez-Garzón et al,2014),该软件包由2个程序组成,第1个程序是msatsi.m,第2个是msatsi_plot.m。程序msatsi.m的功能是完成应力反演工作,根据需求可选择0D(单个网格的应力反演)、1D(应力场随时间变化)、2D、3D和4D(时空分布)5种计算方式;程序msatsi_plot.m的功能是将反演结果绘制出图像。应力反演结果的精度依靠自动重采样方法进行评估,本研究设置的采样次数为2000次,反演应力场参数置信水平的设定范围为95%。
反演结果最终以应力张量解的特征值及其对应的特征向量表示,其中特征值σ1、σ2和σ3分别为最大主应力(主压应力)、中间主应力及最小主应力(主张应力),他们之间的关系为σ1≤σ2≤σ3(以拉张为正)。使用应力形因子R来表征主应力量值间的相对大小关系(Gephart et al,1984)
| $R=\left(\sigma_{2}-\sigma_{1}\right) /\left(\sigma_{3}-\sigma_{1}\right) $ | (1) |
当R=0.5时,应力张量的本征值呈等差排列,反演得到的3个主应力轴在数值上为等间距的,主压应力轴和主张应力轴均确定。随着R不断增大,中间应力本征值逐渐靠近主张应力本征值。在仅考虑偏应力的情况下,中间应力轴也表现为张应力的性质,R值越大,中间应力轴表现的张应力状态越明显。在R=1的极端情况下,中间应力轴和主张应力轴表现的张应力状态一致,此时主张应力轴和中间应力轴交换并不影响应力状态的描述,主张应力轴在与主压应力轴垂直的平面内自由旋转,即呈单轴压缩状态。同理,随着R值自0.5不断减少,中间应力本征值逐渐靠近主压应力本征值,中间应力轴也表现为压应力的性质。R值越小,中间应力轴表现的压应力状态越明显。在R=0的极端情况下,中间应力轴和主压应力轴表现的压应力状态一致,此时压应力轴和中间应力轴交换并不影响应力状态的描述,主压应力轴在与主张应力轴垂直的平面内自由旋转,即呈双轴压缩状态(Gephart et al,1984;万永革等,2011;万永革,2015;黄骥超等,2016)。
2.2 数据从国际地震中心(International Seismological Centre,ISC)获取鄂霍次克微板块及其附近区域1970年1月~2016年12月期间的震源机制解数据。图 1展示了14234个MW≥4地震的震源机制数据,其震源深度h在100km以内的有12858个,在100~200km的有626个,在200~300km的有174个,震源深度大于300km的有576个。本研究参照世界应力图的划分标准(Zoback,1992),根据震源机制解P轴、B轴、T轴倾伏角的大小,将震源机制解类型划分为6种:正断型(NF)、正断兼走滑型(NS)、走滑型(SS)、逆冲兼走滑型(TS)、逆冲型(TF)和不确定型(U),具体分类标准见表 1。对上述地震类型进行统计,逆冲型地震占比例最大。
| 表 1 震源机制解类型划分(据Zoback(1992)) |
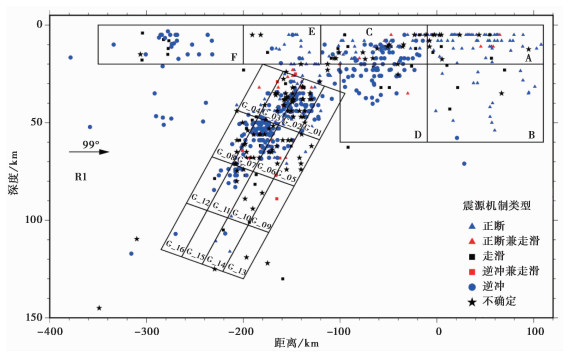
由图 1可以看出,大部分地震分布在俯冲带区域,沿着海沟走向展布。为了便于研究,在日本地区、千岛地区和勘察加地区分别选取一个有代表的区域,即R1、R2和R3(图 1),选取的矩形区域均与各自地区的海沟走向垂直,与俯冲方向近乎一致(Hayes et al,2012)。R1区域宽度为100km,长度为1000km;R2区域宽度为200km,长度为1000km;R3区域宽度为390km,长度为1000km。为了更加清晰直观地观察各个小区域的地震分布特征,将3个区域内的地震数据投影到对应的矩形剖面上,如图 2、图 3、图 4所示,图中各个剖面与海沟交汇点为0km处,剖面走向分别为99°、142°和124°。
|
图 2 R1区域剖面震源机制解类型分布 |

|
图 3 R2区域剖面震源机制解类型分布 |

|
图 4 R3区域剖面震源机制解类型分布 Figure 4 S |
根据Zoback(1992)震源机制类型划分标准,将各个区域内地震进行分类统计。在图 2、图 3和图 4中,根据俯冲板片的轮廓将区域内地震目录事件按照其位置、深度、震源机制类型密集度等标准划分成不同的小区域,其中对浅部俯冲系统的不同部位着重做了区分,比如海沟洋壳一侧的大洋板片上部、弧前大洋板片平缓俯冲段、地幔楔、岛弧区、弧后地区以及陡倾俯冲段等(李天觉等,2019),再使用区域阻尼应力反演方法对各个小分区内的应力场进行反演解算。
3 构造应力场反演结果与分析因为研究区域构造十分复杂,根据不同研究区域的特点,使用不同的划分方法分区,使用0D反演模式得到每个小区域的构造应力场,计算时每个小区域的阻尼因子默认为1.0。反演结果的主要参数包括主压应力轴(σ1)、中间应力轴(σ2)、主张应力轴(σ3)的方位角(azimuth)和倾伏角(plunge)以及应力形因子R值。
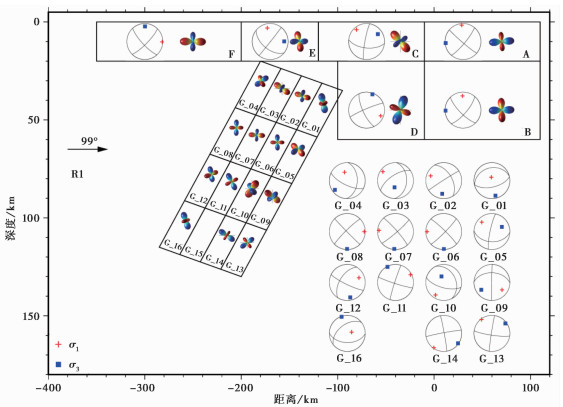
将R1区域细分成A、B、C、D、E、F、G等7个小区域,其中G区域又按照俯冲形状再分成16个小区域。对每一个小区域分别进行构造应力0D反演,应力反演结果如图 5所示。A区域反演得到的主压应力轴(σ1)方位角为163°,倾伏角为79°,主张应力轴(σ3)方位角为281°,倾伏角为5°,应力形因子R为0.3,应力类型为NF(表 2,图 5)。结果显示A区域主张应力轴与太平洋板块俯冲方向基本平行,与日本海沟走向近似垂直,而主压应力轴走向与海沟走向近似平行。分析认为,太平洋板块弯曲,弯曲外侧表现为正断型,局部张力超过板块强度,在俯冲板块弯曲的海沟地区发生张性破裂,多产生正断层型地震。图 5中B区域应力特征与A区域类似,且A、B两区域应力形因子R值均小于0.5,俯冲板片的拖曳作用导致正断型应力。
|
图 5 区域R1应力反演结果 σ1轴和σ3轴最优解为沿剖面走向(99°)里半球投影;主应力空间投影为沿剖面走向(99°)视图;红色代表主压应力轴;蓝色代表主张应力轴 |
| 表 2 区域R1反演得到的应力场参数 |
Zhao(2012)的地震层析成像结果显示,图 5中的C、D区域俯冲板片的俯冲角度约为10°~25°;俯冲板片与上覆板块耦合比较强烈,地震频发。发生在C、D区域内的地震多为逆冲型(TF)地震(图 2)。我们的反演结果显示2个区域的主压应力轴方位角近EW向,与俯冲方向的方位角近似,但是倾伏角有所差别,上部的C区域倾伏角为47°,而下部的D区域倾伏角为21°;2个区域主张应力轴(σ3)的方位角近乎相等,分别为247°和256°,倾伏角有所不同,下部的D区域倾伏角更大,为69°;上部的C区域内应力形因子R值为0.82(表 2),大于D区域;根据应力类型划分标准,C区域为不确定型(U),但是根据其3个主应力轴的倾伏角来看,接近于逆冲型,D区域为逆冲型(TF);上部的C区域所受的构造应力相对于D区域更加复杂。
E区域反演得出主压应力轴(σ1)的方位角为153°,倾伏角为63°;主张应力轴(σ3)的方位角为254°,倾伏角近水平向(1°);应力类型为正断层型(NF),应力形因子R值为0.56;该区域主压应力轴的方位角与俯冲方向不相符,该区域所受构造应力不均匀性较强,可能是因为弧后地区受张性应力环境的影响。F区域反演得到主压应力轴(σ1)的方位角为96°,倾伏角为1°;主张应力轴(σ3)的方位角为190°,倾伏角为73°,近垂直向;应力类型为逆冲型(TF),应力形因子R值为0.65;该区域主压应力轴的方位角与太平洋板块俯冲方向一致。
综上所述,在R1区域的浅部地区(深度20km以内),自海沟洋壳一侧(A区域)逐渐向陆壳一侧延伸的过程中,反演结果显示的构造应力类型是逐渐变化的,即正断型(NF)—逆冲型(TF)—正断型(NF)—逆冲型(TF)(图 5)。
俯冲板片逐渐下插入岩石层和上地幔中,对上覆板块进行推挤,从而多形成逆冲型地震(图 2中G区域)。但是在更具体的不同位置,其地震类型及数量分布有所区别。为了进一步分析不同位置的构造应力特征,对G区域进行细化分区,根据其几何形态划分成等大小的16个小区域,并分别对每个小区域的构造应力场进行反演。研究结果显示G_01、G_02、G_03和G_04小区域深度较浅,所受的构造应力更加复杂,中间区域主压应力轴的方位角与俯冲带俯冲板片的俯冲方位一致,近NWW—SEE向,应力形因子均大于0.7,近似单轴压缩;而两侧区域则有所不同,应力形因子均小于0.5,尤其是右侧(东侧)的G_01区域,其R=0.1,近似于双轴压缩。G_06、G_07和G_08区域主压应力轴的方位角与俯冲板片的俯冲方位一致,倾伏角近乎水平,主张应力轴的倾伏角近乎垂直,应力类型均为逆冲型(TF)。G_05区域主应力轴方位角与前述3个小区域类似,但应力类型为走滑型(SS)。在G_09~G_16震源深度较大的区域内,开始表现出应力类型上下分层的特征:下层的G_09、G_13为不确定型(U),G_10、G_14为正断层型(NF),上层的G_11、G_12、G_16为逆冲型(TF);上层小区域主压应力轴的方位与俯冲方位近似,而下层小区域主张应力轴的范围与俯冲方位近似。我们的反演结果证实了该地区的俯冲深度范围内存在双地震带。
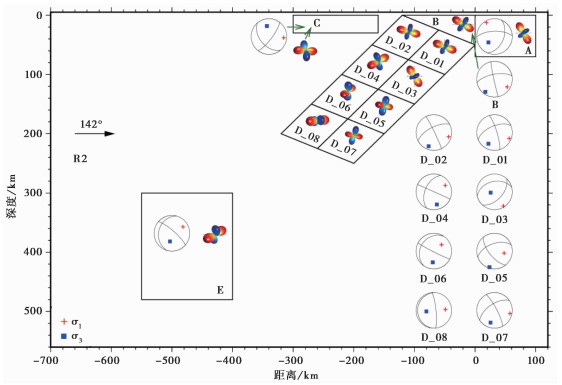
图 6为千岛地区的R2区域反演结果,同样为了方便统计,将R2细分成A、B、C、D、E等5个小区域,其中D区域再细分成8个更小的区域。反演结果显示A区域的主压应力轴(σ1)方位角为161°,倾伏角为58°;主张应力轴(σ3)方位角为20°,倾伏角为26°;应力形因子R值为0.80,应力类型为NF。该区域位于海沟洋壳一侧,处于太平洋板块弯曲拉张应力状态。B、D_01、D_02小区域内主压应力轴的走向与俯冲板片的俯冲方位近乎平行,根据其各个主应力轴的倾伏角大小,B区域和D_01区域的应力类型虽然为U型,但是比较接近逆冲型(TF),应力形因子大于0.5。C区域为弧后地区,该区域的反演结果显示其应力类型为逆冲兼走滑型(TS),主压应力轴方位角与俯冲方向近乎一致。反演结果显示D_03区域的主压应力轴方位角为128,倾伏角为57°;主张应力轴方位角为32°,倾伏角为4°;应力类型为正断层型(NF)。D_04区域主压应力轴方位角为290°,倾伏角为26°;主张应力轴方位角为74°,倾伏角为59°;应力类型为逆冲型(TF)。D_05区域主压应力轴的方位角为95°,倾伏角为8°;主张应力轴的方位角为339°,倾伏角为72°;应力类型为逆冲型(TF)。D_06区域主压应力轴的方位角为269°,倾伏角为28°;主张应力轴的方位角为43°,倾伏角为53°;应力类型为逆冲型(TF)。区域D_05和D_06的主压应力轴方位角与板块俯冲方向近似一致。在深部的D_08区域及E区域,根据其主压应力轴和主张应力轴的倾伏角可知,应力类型均接近于走滑型(SS),主压应力轴的方位与俯冲方位近似(表 3)。
|
图 6 区域R2应力反演结果 σ1轴和σ3轴最优解为沿剖面走向(142°)里半球投影;主应力空间投影为沿剖面走向(142°)视图;红色代表主压应力轴;蓝色代表主张应力轴 |
| 表 3 区域R2反演得到的应力场参数 |
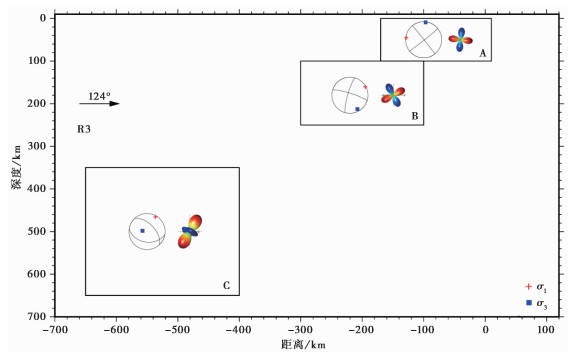
在勘察加地区的R3区域,震源机制数量较少,俯冲带浅部区域震源机制类型也比较单一(图 4)。将该地区分成3个小区域,反演结果显示A区域的主压应力轴的方位角为124°,与俯冲方位近乎平行,倾伏角为7°;主张应力轴的方位角为296°,倾伏角为83°;应力形因子接近0.5,应力类型为逆冲型(TF)(图 7)。B区域的主压应力轴的方位角为301°,与俯冲方位近乎平行,倾伏角为28°;主张应力轴的方位角为95°,倾伏角为59°;应力形因子接近0.5,应力类型为逆冲型(TF)。C区域的主压应力轴的方位角为287°,与俯冲方位近乎平行,倾伏角为59°;主张应力轴的方位角为191°,倾伏角为3°;应力形因子接近0.92,应力类型为正断层型(NF)(表 4)。从该区反演结果(图 7)可以看到,区域自上而下主压应力轴的方位角变化不大,但是倾伏角逐渐增大;在地壳及岩石层区域,俯冲板片对上覆板块进行逆冲推挤,多形成挤压型地震;在350~650km深度范围的地幔中,俯冲板片呈拉张应力状态。
|
图 7 区域R3应力反演结果 σ1轴和σ3轴最优解为沿剖面走向(124°)里半球投影;主应力空间投影为沿剖面走向(124°)视图;红色代表主压应力轴;蓝色代表主张应力轴 |
| 表 4 区域R3反演得到的应力场参数 |
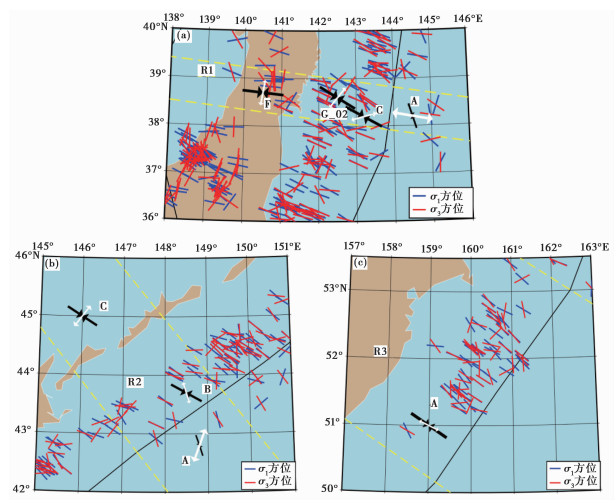
世界应力图计划2008(WSMP 2008)共有21750个应力数据②,其中在鄂霍次克微板块及其附近地区有1502个有效数据,而给出主应力轴方位角和倾伏角的数据有1456个。在该区域内,WSMP2008的应力数据绝大部分是由震源机制解给出,并且深度均小于50km。将区域R1、R2和R3范围内的应力数据的主应力方位分别绘制成图(图 8(a)、8(b)、8(c)),并和对应区域的反演结果主应力轴方位角进行对比。在R1区域内(图 8(a)),A、C、G_02和F区域的反演结果(应力类型和主应力轴方位)与WSMP2008数据基本一致,这里选择G_02区域而不使用E区域,是因为WSMP2008在该经纬度范围内的数据深度为30~50km,与G_02及G_03区域的范围深度更为符合。在R2区域内(8(b)),B和C区域的反演结果(应力类型和主应力轴方位)与WSMP2008数据较为吻合,而A区域的反演结果其应力类型与WSMP2008一致,均为NF型,但主张应力轴方位有所不同,可能是区域内地震类型比较复杂且数量较少(图 3),导致反演结果有稍微偏差。在R3区域内(图 8(c)),A区域的反演结果(应力类型和主应力轴方位)与WSMP2008数据比较吻合,其主压应力轴方位角和板块俯冲方向一致。
|
图 8 世界应力图数据及部分反演结果的主应力方位分布 (a)日本地区;(b)千岛地区;(c)勘察加地区;其中,世界应力图数据来源于WSMP2008(Heidbach et al,2010);蓝色横线表示主压应力轴方位;红色横线表示主张应力轴方位;箭头表示反演结果;黑色箭头表示主压应力轴方位;白色箭头表示主张应力轴方位 |
② http://www.world-stress-map.org
4 讨论根据3个俯冲带区域的剖面分区反演结果,可以归纳出俯冲带区域从浅到深不同的应力场分布特征。
在日本海沟俯冲带地区,浅部区域自海沟附近洋壳一侧逐渐向陆壳一侧延伸的过程中,所受到的构造应力类型是逐渐变化的,即正断型(NF)—逆冲型(TF)—正断型(NF)—逆冲型(TF)。太平洋板块在海沟附近处,顶层区域(A区域)板块张裂,板块中下层(B区域)受俯冲板片下行的拖曳作用(slab pull)而发生弯曲,总体上呈水平拉张的应力环境。自海沟起大洋板块进入低角度的俯冲,对弧前缘(C、D区域)的上覆板块呈强烈挤压作用,而且此处大洋板块与上覆板块耦合较强烈(Uyeda,1992;Christophersen et al,2015;李天觉等,2019)。在岛弧部位(E区域),除了承受来自海沟方向的板块挤压作用以外,随着俯冲板片下潜到深部的含水矿物到达一定深度后失稳脱水、加入到次级对流中,进而导致底辟流上升形成拉张应力环境(Uyeda,1992;Stern,2002;李天觉等,2019)。而距离海沟更远的F区域受大洋板块推挤作用的大环境影响,主要呈现出挤压应力环境。
在大洋板片开始俯冲下行的区域(G区域),较浅部的G_01~G_08主要以逆冲挤压应力环境为主,而在更深的区域(G_09~G_16),表现出上下分层的情况,即上层沿着俯冲方向压缩、下层沿着俯冲方向拉张的应力状态,这种情况属于双地震带“I”型,在日本本州东北、日本关东、千岛-勘察加岛弧等地区均存在(张克亮等,2011)。在海沟处俯冲并弯曲的海洋板块,俯冲到一定深度时会伸直,使其上、下部分分别产生DDC(down-dip compression)、DDT(down-dip tension)的应力分布状态,并到大约200km深度时完全汇合(Hasegawa et al,1978、1994;Yamasaki et al,2003)。
在区域构造应力反演过程中,每个震源机制解权重是一样的,为了防止小震数据过多而掩盖真实信息,将每个区域内7级及以上地震的震源机制解各项参数单独列出进行讨论(表 5、表 6、表 7),表中以发震时间作为每个震源机制的编号。在区域R1内有9个7级及以上地震的震源机制解,均位于浅部区域。其中,震源机制20051114位于A区域,震源机制类型为NF,T轴走向与俯冲方位近似一致。震源机制20121207位于B区域,类型为TF,P轴走向与俯冲方位近似一致;震源机制20110710位于C区域,类型为U,T轴走向为284°,与俯冲方位近似一致;在海沟附近地区,海沟展布不是严格的直线以及震中定位可能有偏差,20110710、20121207这2个地震投影到剖面时位于x=0附近,因此,2个震源机制的类型与区域应力反演结果不一致也属于正常情况。震源机制19810118和20050816均位于G_03小区域,TF类型,P轴走向与俯冲方位近似一致,与区域反演结果一致。震源机制20030526和20110407位于G_08小区域,TF类型,P轴走向与俯冲方位近似一致,与区域反演结果也一致。震源机制20110309和20110311位于C区域,TF类型,P轴走向与俯冲方位近似一致;x=-102及x=-116(图 2、图 5),处于俯冲板块与上覆板块耦合强烈的地区(C区域)。
| 表 5 区域R1内7级及以上地震震源机制解各项参数 |
| 表 6 区域R2内7级及以上地震震源机制解各项参数 |
| 表 7 区域R3内7级及以上地震震源机制解各项参数 |
千岛地区的地震资料分布和反演结果显示,该地区俯冲板片倾角变化不大,海沟洋壳一侧受板块弯曲作用呈拉张状态,海沟陆壳一侧受大洋板块的挤压作用,主压应力轴的方位呈NWW向,且接近于水平。而在俯冲带上应力场随深度不同发生变化,较为浅部的区域(D_01、D_02)主要以挤压应力类型为主,主压应力走向与俯冲方向一致;D_03和D_04区域呈现双地震带“I”型特征,在D_03区域为拉张应力环境,D_04区域为挤压应力环境;而在D_05和D_06区域,双地震带汇合(到200km深度左右),均呈挤压应力环境。在300~450km深处的E区域,主压应力轴接近俯冲带走向,但是整个区域地震资料较分散,U型和SS型震源机制解数量占比较大,应力场不均匀性较强。本文反演的结果与吴忠良等(1989)利用地震资料统计P、T轴的走向和倾伏角等信息得出的结果类似,并与Christova(2015)采用FMSIA方法描绘千岛地区不同深度区域的构造应力场图像结果相似。千岛俯冲带地区浅部区域主要的地球动力学驱动力是板片拉力(slab pull)和洋脊推力,在中部深度区域伸直的板片处观察到双层地震应力图像,而在深部区域出现的应力场不均匀性主要是由于地幔阻力所导致(Christova,2015)。在R2区域内,7级及以上地震的震源机制解共有5个(表 6)。其中震源机制19780323、19840324和19941109位于B区域,且均为TF类型,与区域应力反演结果一致,P轴走向与俯冲方位近似一致。震源机制19941004位于D_01小区域,为TS类型,P轴走向与俯冲方位近似一致。震源机制19781206位于D_08小区域,属于中源地震,与区域应力场反演结果一致。
在勘察加地区,本研究所采用的ISC震源机制解数据量较少,故在分区时只按照深度划分了3个小区域。由图 1和图 4可见,在海沟洋壳一侧也存在少量正断型地震,而在陆壳一侧以逆冲型地震为主,浅部区域的应力类型分布状态与千岛海沟地区类似,在图 4中,距离海沟200~300km的浅部地区存在有少量正断型地震,可能与弧后扩张有关;俯冲带中部区域(B区域)主要为挤压型应力特征,主压应力轴的方位也与俯冲方位一致;而在深部区域(C区域)主要呈拉张型应力状态,俯冲板片的拖曳力导致俯冲带前缘板片平行受压,板片内部向下延伸至平行方向(Christova,2001)。在R3范围内7级及以上地震的震源机制解有5个(表 7),其中震源机制19930608和19931113位于A区域,均为TF类型,P轴走向与俯冲方位近似一致,各项参数符合区域构造应力反演结果。高原等(1995)用宽频带波型拟合方法研究了震源机制解19931113的破裂过程,研究表明复杂的破裂图像与该地区的地壳结构和构造应力场具有直接的关系,太平洋板块的挤压在此处比较强烈,并且是导致这次地震的主要成因。震源机制20160130位于B区域,类型为NS,P轴走向与俯冲方位近似一致。震源机制20081124和20130524位于C区域,类型为U,P轴走向与俯冲方位近似一致,倾伏角较大,而T轴倾伏角较小,近似于拉张型。
ISC提供的地震震源机制解数据其震源深度有一定的误差,但是误差范围相对较小,因此,震源深度误差并不影响本文的反演结果。综上所述,在整个鄂霍次克微板块东部俯冲带地区,日本海沟、千岛海沟和勘察加海沟3个不同区域所受应力场特征既有相似之处,又存在各自的特点,西北太平洋板块对鄂霍次克微板块的强烈俯冲是整个俯冲带地区挤压型应力场的主要来源,而3个区域的俯冲板片不同俯冲角度以及上覆板块的地质特征差异造成了其各自二阶应力场差异。
5 结论通过使用MSATSI软件,对鄂霍次克微板块东部俯冲带地区不同区域的震源机制解资料进行构造应力场反演,反演得到的剖面应力场图像展示了不同深度区域的应力分布特征,主要得到以下结论:
(1) 在日本海沟、千岛海沟和勘察加海沟地区的浅部区域水平面内的主压应力轴与西北太平洋板块的俯冲方位一致,与海沟走向近似垂直。海沟地区洋壳一侧以拉张型应力状态为主,陆壳一侧以挤压型应力为主,且在弧后区域均存在拉张的应力状态;80~200km深度范围区域表现出双地震带“I”型构造应力场特征。
(2) 日本海沟地区的俯冲带由于俯冲角较小(相对于千岛和勘察加海沟地区),水平方向沿北西西向延伸更远,大洋板块与上覆板块之间耦合更加强烈,逆冲型地震发生数量最多。
(3) 对于深部区域(h>300km),千岛地区应力场表现出非均匀性特征,可能是由地幔阻力导致的;而勘察加地区应力场表现出拉张型,可能是因为俯冲板片的拉伸拖曳作用更强。
致谢: 本文图件使用开源软件GMT软件绘制,主应力空间图样部分的绘图程序由万永革研究员提供,黄骥超对本文计算部分提供了帮助,匿名审稿专家对本文提出了建设性的修改意见,在此一并表示衷心感谢。
崔华伟、万永革、黄骥超等, 2019, 帕米尔-兴都库什地区构造应力场反演及拆离板片应力形因子特征研究, 地球物理学报, 62(5): 1633-1649. |
高祥林、罗焕炎、平原和郎, 1994, 日本俯冲带应力产生与传播的数值模拟, 地震地质, 16(2): 97-108. |
高原、吴忠良, 1995, 1993年11月13日堪察加大地震的破裂过程及其构造意义, 地球物理学报, 38(1): 55-63. DOI:10.3321/j.issn:0001-5733.1995.01.007 |
何建坤、刘福田, 1998, 俯冲板片形貌特征和活动大陆边缘演化体制的关系, 地球物理学进展, 13(2): 15-25. |
黄骥超、万永革、盛书中等, 2016, 汤加-克马德克俯冲带现今非均匀应力场特征及其动力学意义, 地球物理学报, 59(2): 578-592. |
黄玺英、魏东平、陈棋福等, 2003, 全球观测应力场的短波分量分析, 地震学报, 25(1): 40-46. DOI:10.3321/j.issn:0253-3782.2003.01.005 |
黄玺英、魏东平, 2004, 全球板块运动对板块边界带应力场的影响, 中国科学院研究生院学报, 21(2): 227-232. |
李天觉、陈棋福, 2019, 西北太平洋俯冲带日本本州至中国东北段应力场反演, 地球物理学报, 62(2): 520-533. |
宁杰远、臧绍先, 1987, 日本海及中国东北地震的深度分布及其应力状态, 地震地质, 9(2): 49-61. |
任建业、李思田, 2000, 西太平洋边缘海盆地的扩张过程和动力学背景, 地学前缘, 7(3): 203-213. DOI:10.3321/j.issn:1005-2321.2000.03.019 |
孙文斌、和跃时, 2004, 西太平洋Benioff带的形态及其应力状态, 地球物理学报, 47(3): 433-440. DOI:10.3321/j.issn:0001-5733.2004.03.011 |
孙振添、魏东平、韩鹏等, 2013, 板块运动与地震各向异性及应力场的相关性统计分析, 地震学报, 35(6): 785-798. DOI:10.3969/j.issn.0253-3782.2013.06.002 |
Uyeda S, 1992.日本岛弧和俯冲作用.潘秋霞, 译.海洋地质翻丛, (4): 41~46.
|
万永革, 2015, 联合采用定性和定量断层资料的应力张量反演方法及在乌鲁木齐地区的应用, 地球物理学报, 58(9): 3144-3156. |
万永革、盛书中、许儒雅等, 2011, 不同应力状态和摩擦系数对综合P波辐射花样影响的模拟研究, 地球物理学报, 54(4): 994-1001. DOI:10.3969/j.issn.0001-5733.2011.04.014 |
王晓山、吕坚、谢祖军等, 2015, 南北地震带震源机制解与构造应力场特征, 地球物理学报, 58(11): 4149-4162. |
吴忠良、臧绍先, 1989, 千岛-鄂霍次克海地区的地震分布、震源机制及应力状态, 地震地质, 11(2): 85-95. |
谢富仁、崔效锋、赵建涛, 2003, 全球应力场与构造分析, 地学前缘, 10(增刊Ⅰ): 22-30. |
徐纪人、赵志新、河野芳辉等, 2003, 日本南海海槽地震区域应力场及其板块构造动力学特征, 地球物理学报, 46(4): 488-494. DOI:10.3321/j.issn:0001-5733.2003.04.010 |
徐纪人、赵志新、石川有三, 2008, 中国大陆地壳应力场与构造运动区域特征研究, 地球物理学报, 51(3): 770-781. DOI:10.3321/j.issn:0001-5733.2008.03.018 |
许忠淮、汪素云、黄雨蕊等, 1989, 由大量的地震资料推断的我国大陆构造应力场, 地球物理学报, 32(6): 636-647. DOI:10.3321/j.issn:0001-5733.1989.06.004 |
许忠淮、阎明、赵仲和, 1983, 由多个小地震推断的华北地区构造应力场的方向, 地震学报, 5(3): 268-279. |
杨佳佳、张永庆、谢富仁, 2018, 日本海沟俯冲带MW9.0地震震源区应力场演化分析, 地球物理学报, 61(4): 1307-1324. |
臧绍先、宁杰远, 1996, 西太平洋俯冲带的研究及其动力学意义, 地球物理学报, 39(2): 188-202. DOI:10.3321/j.issn:0001-5733.1996.02.006 |
张克亮、魏东平, 2008, 环太平洋俯冲带内双地震带及其成因机制研究进展, 地球物理学进展, 23(1): 31-39. |
张克亮、魏东平, 2011, 双地震带的影响因素探讨, 地球物理学报, 54(11): 2838-2850. DOI:10.3969/j.issn.0001-5733.2011.11.014 |
郑建常、王鹏、李冬梅等, 2013, 使用小震震源机制解研究山东地区背景应力场, 地震学报, 35(6): 773-784. DOI:10.3969/j.issn.0253-3782.2013.06.001 |
Angelier J, 1984, Tectonic analysis of fault slip data sets., J Geophys Res Solid Earth, 89(B7): 5835-5849. DOI:10.1029/JB089iB07p05835 |
Bott M H P, 1959, The mechanics of oblique slip faulting, Geological Magazine, 96(2): 109-117. DOI:10.1017/S0016756800059987 |
Christophersen A, Berryman K, Litchfield N, 2015. The GEM Faulted Earth Project, Version 1.0. GEM Technical Report 2015-02 V1.0.0.
|
Christova C, 2001, Depth distribution of stresses in the Kamchatka Wadati-Benioff zone inferred by inversion of earthquake focal mechanisms, J Geodyn, 31(4): 352-372. |
Christova C, 2004, Stress field in the Ryukyu-Kyushu Wadati-Benioff zone by inversion of earthquake focal mechanisms, Tectonophysics, 384(1-4): 175-189. DOI:10.1016/j.tecto.2004.03.010 |
Christova C, 2005, Space distribution of the contemporary stress field in the Izu-Bonin Wadati-Benioff zone by inversion of earthquake focal mechanisms, J Geodyn, 39(4): 413-428. DOI:10.1016/j.jog.2005.03.002 |
Christova C, Scholz C H, 2003, Stresses in the Vanuatu subducting slab:A test of two hypotheses, Geophys Res Lett, 30(15): 1790. DOI:10.1029/2003GL017701 |
Christova C, Tsapanos T, 2000, Depth distribution of stresses in the Hokkaido Wadati-Benioff zone as deduced by inversion of earthquake focal mechanisms, J Geodyn, 30(5): 557-573. DOI:10.1016/S0264-3707(00)00009-0 |
Christova C V, 2015, Spatial distribution of the contemporary stress field in the Kurile Wadati-Benioff zone by inversion of earthquake focal mechanisms, J Geodyn, 83: 1-17. DOI:10.1016/j.jog.2014.11.001 |
DeMets C, Gordon R G, Argus D F, 2010, Geologically current plate motions, Geophys J Int, 181(1): 1-80. |
Gephart J W, Forsyth D W, 1984, An improved method for determining the regional stress tensor using earthquake focal mechanism data:Application to the San Fernando Earthquake Sequence, J Geophys Res:Solid Earth, 89(B11): 9305-9320. DOI:10.1029/JB089iB11p09305 |
Hardebeck J L, Michael A J, 2006, Damped regional-scale stress inversions:Methodology and examples for southern California and the Coalinga aftershock sequence, J Geophys Res:Solid Earth, 111(B11): B11310. |
Hasegawa A, Horiuchi S, Umino N, 1994, Seismic structure of the northeastern Japan convergent margin:A synthesis, J Geophys Res:Solid Earth, 99(B11): 22295-22311. DOI:10.1029/93JB02797 |
Hasegawa A, Umino N, Takagi A, 1978, Double-planed structure of the deep seismic zone in the northeastern Japan arc, Tectonophysics, 47(1-2): 43-58. DOI:10.1016/0040-1951(78)90150-6 |
Hayes G P, Wald D J, Johnson R L, 2012, Slab1.0:A three-dimensional model of global subduction zone geometries, J Geophys Res:Solid Earth, 117(B1): B01302. |
Heidbach O, Tingay M, Barth A, et al, 2010, Global crustal stress pattern based on the World Stress Map database release 2008, Tectonophysics, 482(1-4): 3-15. DOI:10.1016/j.tecto.2009.07.023 |
Konstantinou K I, Mouslopoulou V, Liang W T, et al, 2017, Present-day crustal stress field in Greece inferred from regional-scale damped inversion of earthquake focal mechanisms, J Geophys Res:Solid Earth, 122(1): 506-523. DOI:10.1002/2016JB013272 |
Kumar A, Wagner L S, Beck S L, et al, 2016, Seismicity and state of stress in the central and southern Peruvian flat slab, Earth Planet Sci Lett, 441: 71-80. DOI:10.1016/j.epsl.2016.02.023 |
Levin V, Shapiro N, Park J, et al, 2002, Seismic evidence for catastrophic slab loss beneath Kamchatka, Nature, 418(6899): 763-767. DOI:10.1038/nature00973 |
Martínez-Garzón P, Kwiatek G, Bohnhoff M, et al, 2014, MSATSI:A MATLAB package for stress inversion combining solid classic methodology, a new simplified user-handling, and a visualization tool, Seismol Res Lett, 85(4): 896-904. DOI:10.1785/0220130189 |
Matsumoto S, Nakao S, Ohkura T, et al, 2015, Spatial heterogeneities in tectonic stress in Kyushu, Japan and their relation to a major shear zone, Earth Planets Space, 67: 172. DOI:10.1186/s40623-015-0342-8 |
Meighan H E, Pulliam J, Ten Brink U, et al, 2013, Seismic evidence for a slab tear at the Puerto Rico Trench, J Geophys Res:Solid Earth, 118(6): 2915-2923. DOI:10.1002/jgrb.50227 |
Michael A J, 1984, Determination of stress from slip data:Faults and folds, J Geophys Res, 89(B13): 11517-11526. DOI:10.1029/JB089iB13p11517 |
Seno T, Sakurai T, Stein S, 1996, Can the Okhotsk plate be discriminated from the North American plate?, J Geophys Res:Solid Earth, 101(B5): 11305-11315. DOI:10.1029/96JB00532 |
Stern R J, 2002, Subduction zones, Rev Geophys, 40(4): 3-1-3-38. |
Wada I, Mazzotti S, Wang K, 2010, Intraslab stresses in the cascadia subduction zone from inversion of earthquake focal mechanisms, Bull Seismol Am, 100(5A): 2002-2013. DOI:10.1785/0120090349 |
Wallace R E, 1951, Geometry of shearing stress and relation to faulting, J Geol, 59(2): 118-130. |
Wan Y G, 2010, Contemporary tectonic stress field in China, Earthq Sci, 23(4): 377-386. DOI:10.1007/s11589-010-0735-5 |
Wan Y G, Sheng S Z, Huang J C, et al, 2016, The grid search algorithm of tectonic stress tensor based on focal mechanism data and its application in the boundary zone of China, Vietnam and Laos, J Earth Sci, 27(5): 777-785. DOI:10.1007/s12583-015-0649-1 |
Wessel P, Uieda L, Luis J M F, et al, 2017. The generic mapping tools 6: Classic versus modern mode. In: AGU Fall Meeting, AGU Fall Meeting Abstracts. AGU. https://ui.adsabs.harvard.edu/abs/2017AGUFMIN44A.02W/abstract.
|
Wu W N, Lo C L, Lin J Y, 2017, Spatial variations of the crustal stress field in the Philippine region from inversion of earthquake focal mechanisms and their tectonic implications, J Asian Earth Sci, 142: 109-118. DOI:10.1016/j.jseaes.2017.01.036 |
Xu P L, 2004, Determination of regional stress tensors from fault-slip data, Geophys J Int, 157(3): 1316-1330. DOI:10.1111/j.1365-246X.2004.02271.x |
Xu Z G, Huang Z C, Wang L S, et al, 2016, Crustal stress field in Yunnan:implication for crust-mantle coupling, Earthq Sci, 29(2): 105-115. DOI:10.1007/s11589-016-0146-3 |
Yamasaki T, Seno T, 2003, Double seismic zone and dehydration embrittlement of the subducting slab, J Geophys Res:Solid Earth, 108(B4): 2212-2232. |
Yoshida K, Hasegawa A, Okada T, 2016, Heterogeneous stress field in the source area of the 2003 M6.4 Northern Miyagi Prefecture, NE Japan, earthquake, Geophys J Int, 206(1): 408-419. |
Zhao D P, 2012, Tomography and dynamics of Western-Pacific subduction zones, Monogr Environ Earth Planets, 1(1): 1-70. DOI:10.5047/meep.2012.00101.0001 |
Zoback M L, 1992, First-and second-order patterns of stress in the lithosphere:the World Stress Map Project, J Geophys Res:Solid Earth, 97(B8): 11703-11728. DOI:10.1029/92JB00132 |
 2020, Vol. 36
2020, Vol. 36



