南海西缘走滑带中南段的热模拟研究
方桂, 张健, 王蓓羽, 艾依飞, 董淼
中国地震  2020, Vol. 36 2020, Vol. 36 Issue (2): 221-233 Issue (2): 221-233
|
南海是中国唯一具有洋壳结构的边缘海,海盆两侧的被动陆缘上形成了多个沉积盆地,无论在地质基础理论方面还是油气资源方面,均具有重要的研究意义(姚永坚等,2018)。从20世纪80年代开始,国内外许多专家学者针对南海的构造演化和热历史开展了相关的研究工作,也取得了一定的研究成果。但是,目前国内外对南海西缘走滑带的研究大多只是关于构造特征的研究,对西缘走滑带的热效应研究还相对欠缺(张健等,2000;唐晓音等,2014)。因此,本文针对南海西缘走滑带中南段进行热模拟,旨在分析其在走滑过程中的热效应,以丰富对南海西缘走滑带的热动力学研究。
南海西缘是南海陆缘中结构构造最复杂、研究程度相对较低的海陆构造边界,同时也是研究走滑带周缘新生代盆地构造热演化史的重要地区(孟林等,2014)。前人依据大规模的南海地质、地球物理综合调查资料,已对西缘走滑带的岩石圈圈层结构、海底热流活动等开展了许多研究,西缘走滑断裂带是走滑活动的集中地带,其热效应与海底热流活动及其走滑活动等密切相关(刘海龄等,2015;王鹏程等,2017)。在前人的研究基础上,开展对西缘走滑带中南段热效应的数值模拟研究,计算该带因发生走滑摩擦而产生的温度和热流范围,为研究西缘走滑带地区地震的孕育过程提供相应的热动力学依据。
虽然前人对西缘走滑带以及其邻近地区进行了大量的理论研究和实际观测,但是对该带在发生主要走滑活动以来的走滑生热史的研究还相对欠缺,仍有许多问题还未解决(周蒂等,2002;高红芳,2011)。本文基于定性的走滑带地质模型,通过数值计算,开展对该带热效应的定量研究,分析海底热流活动与走滑断层摩擦生热的关系,为研究西缘走滑带周缘新生代盆地中烃源岩的热史及成熟史提供了基础理论依据,为该带周缘盆地的油气勘探潜力评价提供理论支撑。
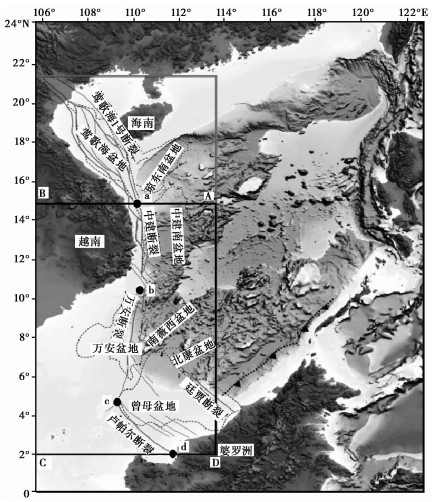
1 构造特征西缘走滑带总体呈NS向展布(105°E~113°E,2°N~21°N),走滑带中段越东断裂全长约500km,向南经过中建南盆地,延伸至万安盆地与走滑带南段万安断裂相连,万安断裂全长约800km。万安断裂继续向SE延伸至加里曼丹岛西北部,与NW向展布的卢帕尔断裂相接,一起形成NS向规模宏大的断裂系统(Lü et al,2012),西缘断裂系统如图 1所示。
|
图 1 西缘断裂系统分布(据刘海龄等(2015)) |
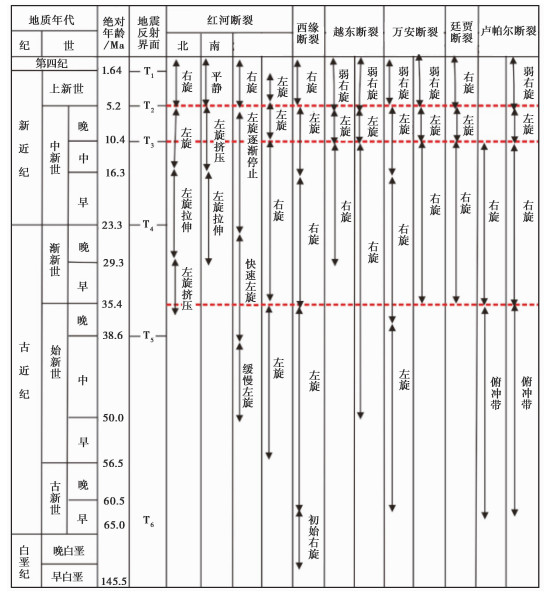
南海西缘整条断裂带均具有明显的伸展和走滑现象,走滑带中南段两侧地块沉积层主要由湿石英岩组成,平均厚度约为2km;上地壳主要由湿石英岩组成,平均厚度约为12km;下地壳主要由斜长岩组成,平均厚度约为10km(Morley,2002)。西缘走滑带的走滑运动具有多期次活动、左-右旋向交替转换的显著特征。综合前人的研究结果,对该走滑带的活动期次及旋向进行了总结,如图 2所示。
|
图 2 西缘断裂带走滑活动期次和旋向(据高红芳(2011)) |
由图 2可见,西缘走滑带中段(越东断裂)在距今50Ma至10Ma发生了较漫长的右旋走滑活动,在距今10Ma至5Ma经历了短暂的左旋活动,而从距今5Ma到现今则以弱右旋或右旋活动为主;而南段(万安断裂、卢帕尔断裂)则在距今35Ma至10Ma发生了右旋活动,之后构造发生反转,在距今10Ma至5Ma变为短暂的左旋活动,而从距今5Ma到现今则以弱右旋或右旋活动为主,整个断裂带在走滑活动历史时期的平均走滑速率大约为0.5cm/a(刘海龄,1999)。依据上述走滑带构造特征,本文建立数值模型,对走滑带中南段的热效应进行计算。
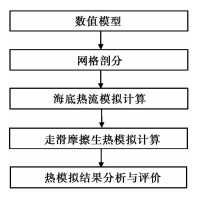
2 数值模拟基于上述西缘走滑带中南段的构造特征研究结果,运用数值软件Comsol进行数值计算,计算流程如图 3所示。
|
图 3 模拟计算流程 |
首先,需要根据走滑带的构造特征建立相应的地质模型,再对模型进行网格剖分;其次,通过建立固体传热场和摩擦生热场,分别对海底热流传热和走滑带走滑摩擦生热进行模拟计算;最后,对热模拟计算结果进行分析和评价。
2.1 数值模型搭建根据西缘走滑带地质地形图,框选出矩形研究区域ABCD,并确定各断裂带的分界点a、b、c、d,从而确定各断裂带的具体位置(图 1),其中ab段为越东断裂,bc段为万安断裂,cd段为卢帕尔断裂。
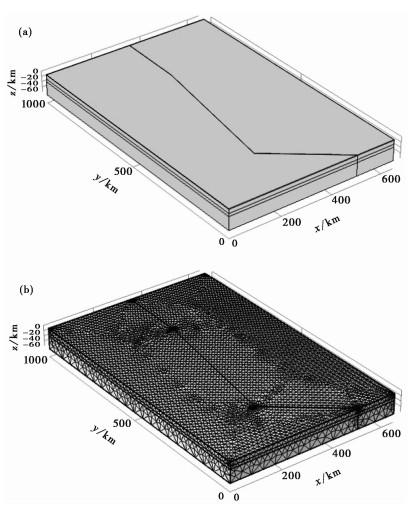
从框选区域ABCD提取相关几何参数,得到ab段越东断裂长度为500km,bc段万安断裂长度为800km,cd段卢帕尔断裂长度为650km。结合前人对西缘走滑带中南段岩石圈圈层结构的研究结果(林长松等,2009),将模型定义为4层分层结构,模型表层为沉积层(厚度取2km),中间2层分别为上地壳(厚度取12km)和下地壳(厚度取10km),底层为地幔(厚度取46km),模型总厚度为70km,搭建三维地质模型,如图 4(a)所示。模型各层主要组成物质:沉积层和上地壳为湿石英岩,下地壳为斜长岩,地幔为湿橄榄岩。参照前人在南海西南海盆构造演化的热模拟研究中给予岩石圈各层物质的物性参数值(张健等,2005;余尚江等,2019),并结合西缘走滑带的实际情况,给定模型各层组成物质的密度、恒压比热容、生热率、热导率等参数值,如表 1所示。
|
图 4 西缘走滑带中南段三维模型(a)及网格剖分结果(b) |
| 表 1 走滑带中南段热模拟物质参数 |
进行热模拟数值计算之前,需对模型进行网格剖分。一般而言,网格剖分越精细,数值求解结果越精确,但计算耗时也越长。通过测试,本文确定了一个最优的网格剖分方案,具体参数见表 2。
| 表 2 网格化单元参数 |
利用表 2给定的网格化单元化参数,对走滑带地质模型进行网格剖分,如图 4(b)所示。
2.3 海底热流传热模拟在进行热模拟计算前,需先建立相应的热场。西缘走滑带的热效应主要来源于两部分,即海底热流向上传导的热和走滑带走滑摩擦产生的热。对于海底热流向上传热部分,需构建固体传热场来进行计算。根据傅里叶导热定律,热量总是从高温物体流向低温物体,且热流量与温度梯度成正比,比例系数为K,称作热导系数(张健等,2017),可表示为
| $q=-K \nabla T $ | (1) |
其中,q为热流密度(mW/m2),K为热导系数(W/(m·℃)),▽T为地温梯度(℃/m)。温度T的变化率为
| $\rho C \frac{\partial T}{\partial t}=\nabla \cdot(-q)+A $ | (2) |
联立式(1)、(2),则可得到固体热传导方程为
| $\rho C \frac{\partial T}{\partial t}=\nabla \cdot(K \nabla T)+A $ | (3) |
其中,ρ为密度(kg/m3),C为恒压比热容(J/(kg·℃)),t为时间(s),A为生热率(μW/m3)。
考虑到走滑带中南段的海底热流主要来源于深部的地幔热,且至今为止,莫霍面处的热流仍有60~90mW/m2。同时,参考Gemmer等(2002)对北海东部的三维热模拟过程,给定海底热流传热的边界条件,模型顶部边界定义为恒温边界,给定温度值T0=10℃,底部边界为热流边界,给定热流值Q0=40mW/m2,模型其余外部边界均为绝热边界,进行海底热流传热稳态模拟计算,结果如图 5所示。

|
图 5 海底热流传热稳态模拟计算温度(a)及热流分布结果(b) |
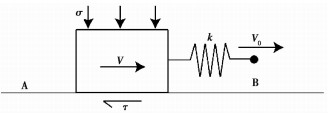
在进行走滑摩擦生热模拟计算前,需先建立摩擦生热场。参考Kato(2001)对摩擦生热模型的研究,采用一维弹簧-滑块模型模拟走滑断层,如图 6所示。该模型以滑块沿面A滑动摩擦而产生的热来模拟走滑断层因走滑摩擦而产生的热。
|
图 6 一维弹簧-滑块模型 |
滑块底部与面A之间的接触面代表走滑断层两盘走滑时的接触面,弹簧代表走滑断层周围的弹性介质。滑块底部受到的摩擦应力τ大小为
| $\tau=k\left(u_{0}-u\right) $ | (4) |
其中,k为弹簧弹性系数,u0为载荷点B的位移(m),u为滑块的位移(m)。滑块受到的摩擦应力τ应遵循“速度-状态-温度摩擦定律” (Zhang et al,2011)
| $\tau=\mu \sigma $ | (5) |
其中,σ为滑块所受到的有效压应力(Pa),μ为接触面的摩擦系数,其表达式为
| $\mu=\mu_{0}+a\left[\ln \left(\frac{V}{V_{0}}\right)+\frac{Q_{a}}{R}\left(\frac{1}{T}-\frac{1}{T_{0}}\right)\right]+b \theta $ | (6) |
其中,μ0为当V=V0、T=T0时的参考摩擦系数,V为滑块滑动速度(m/s),T为绝对温度(K),a和b为与实验有关的摩擦参数,Qa为表面激活能(KJ/mol),V0为参考速度(m/s),T0为参考温度(K),R为气体常数,θ表示滑块与面A之间的滑动接触状态。滑块的控制方程为
| $\frac{\mathrm{d} \tau}{\mathrm{d} t}=k\left(V_{0}-V\right) $ | (7) |
其中,τ为滑块所受的摩擦应力(Pa),V0为载荷点B的参考速度(m/s),V为滑块运动速度(m/s),k为弹簧弹性系数,也称断层刚度。
相比于海底热流传热模拟,摩擦生热模拟需定义热接触边界,即走滑断层接触面边界条件。参考尹凤玲等(2018)对板块挤压碰撞应力的研究结果,给定模型两盘之间的接触压力为3MPa。结合走滑带的断层面情况,给定模型两盘的相对走滑平均速率为4.5mm/a,模型两盘的接触面粗糙平均高度为0.4m,粗糙平均斜率为0.8(闫伟等,2013)。考虑到走滑带发生主要走滑活动的时间,给定模拟总时间为30Ma,在计算过程中时间步长取0.1Ma。选取4个时间节点t=0、t=10Ma、t=20Ma、t=30Ma的温度和热流分布进行成图,结果如图 7、图 8所示。

|
图 7 摩擦生热模拟温度结果 |
|
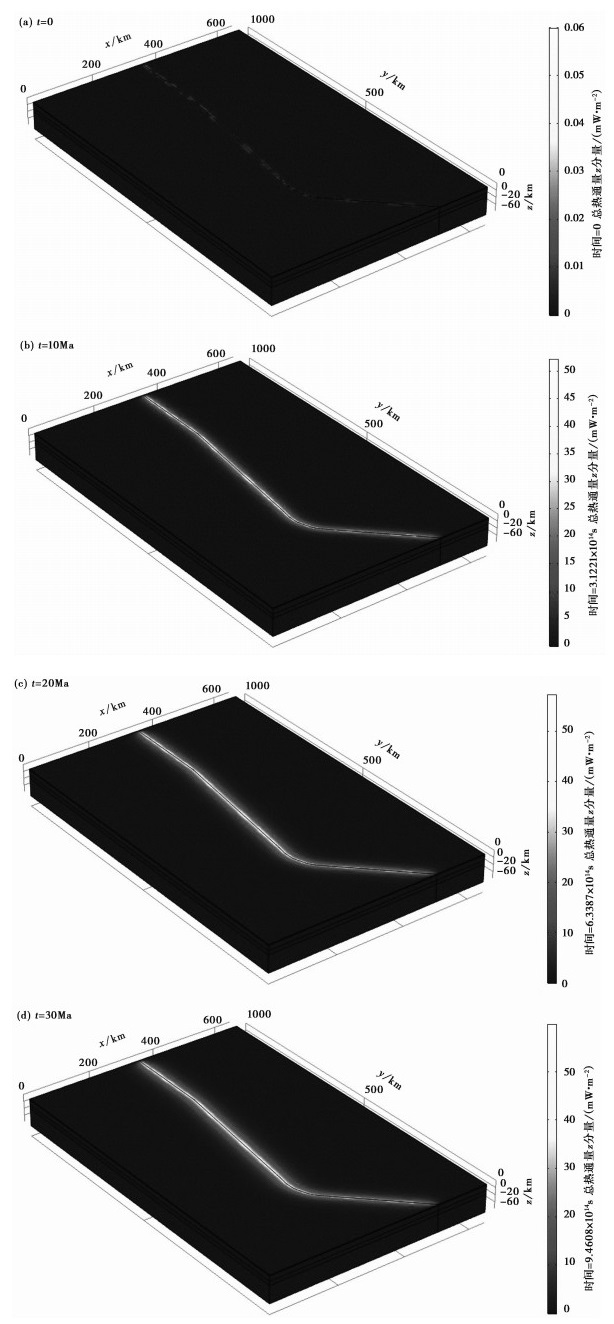
图 8 摩擦生热模拟热流结果 |
由图 5可见,海底热流向上传导达到稳态时,岩石圈温度的分布情况由地幔向上逐渐降低,地幔温度大致在1000~1200℃,最高温度达到1270℃;莫霍面处的温度大约为1000℃,莫霍面处的热流约为55mW/m2。
3.1.2 模拟结果评价参考南海西缘地区的相关地质资料(Gao et al,2012),现今西缘地区莫霍面处的热流为50~90mW/m2,莫霍面处温度为800~1000℃,地幔温度在1300℃左右。而根据本文模拟的结果,地幔温度为1000~1200℃,莫霍面处温度约为1000℃,莫霍面处的热流约为55mW/m2,海底热流传热模拟结果与实际情况基本相符。
3.2 摩擦生热 3.2.1 模拟结果分析由图 7、图 8可见,随时间推移,走滑断层开始发生走滑摩擦,热量逐渐生成。当时间t=10Ma时,断层接触面温度已明显升高,中南段越东-万安断裂接触面温度约为250℃,热流约为40mW/m2;南段卢帕尔断裂接触面温度则低一些,为200℃左右,热流约为30mW/m2。随着断层继续走滑,热量持续生成并累积。当时间t=20Ma时,中南段越东-万安断裂接触面温度约为350℃,热流约为50mW/m2;南段卢帕尔断裂接触面温度为250℃左右,热流约为35mW/m2。当时间t=30Ma时,中南段越东-万安断裂接触面温度约为400℃,热流约为55mW/m2;南段卢帕尔断裂接触面温度在300℃左右,热流约为40mW/m2。从计算结果可以看出,走滑接触面在不断产热的同时,产生的热量也在沿接触面法线方向不断向外扩散,且中南段越东-万安断裂的生热量整体高于南段卢帕尔断裂。
根据本文热模拟结果可以推测,西缘走滑带中南段在发生主要走滑活动的地质历史时期,由于走滑摩擦而产热,在70km深度范围内,其断裂面最高温度可达434℃,最大热流可达55mW/m2。
3.2.2 模拟结果评价参考广州海洋地质调查局在南海西缘地区的海底热流实测值①,对模拟结果进行评价。根据实测热流结果可知,走滑带中南段越东-万安断裂的热流值基本为110mW/m2左右,南段卢帕尔断裂热流值稍低,为90mW/m2左右。由于实测海底热流值是走滑带走滑摩擦与海底热流向上传热的综合响应,因此在对摩擦生热结果进行评价时,需将走滑摩擦产生的热流与海底热流传导产生的热流相加,再与实测海底热流值进行比较。模拟结果评价见表 3。
| 表 3 摩擦生热模拟结果评价(单位:mW/m2) |
① 徐行,2018.南海地热流探测与分析.广州海洋地质调查局内部资料.
将走滑带中南段越东万安断裂因走滑摩擦产生的热流与海底热流传导产生的热流相加,得到综合热流值为115mW/m2,与实测海底热流值110mW/m2相比,相对误差为4.5%;将走滑带南段卢帕尔断裂因走滑摩擦产生的热流与海底热流传导产生的热流相加,得到综合热流值为100mW/m2,与实测海底热流值90mW/m2相比,相对误差为11.1%,模拟结果误差控制在15%以内。
3.3 热模拟结果与地震孕育的关系分析根据本文模型计算得出,该地区走滑带中南段在距今约30Ma时间尺度下的由于走滑摩擦所产生的最大热流在40~55mW/m2之间,该热流值相对较小,说明该带走滑摩擦作用较弱。因此,可以推断出该走滑带活动较为缓慢,断层两盘无强烈的挤压,热应力无法在较短时间内快速累积,属于较为稳定的走滑断层,不具备地震成核和孕育的相关条件,基本不会产生较大的地震。
4 结论本文模拟计算了西缘走滑带中南段在距今约30Ma时间尺度下因走滑摩擦而产生的温度和热流。热模拟计算结果表明,中南段越东-万安断裂在距今约30Ma时间尺度下、70km深度范围内,由于走滑摩擦而产生的最高温度约为434℃,产生的最大热流约为55mW/m2;而南段卢帕尔断裂在相同的时间尺度和深度范围内,由于走滑摩擦而产生的最高温度约为300℃,产生的最大热流约为40mW/m2;模拟结果与实测结果相比,误差控制在15%以内。根据本文模拟计算结果,可分析该走滑带在新生代的走滑生热史,为研究走滑带周缘新生代盆地中烃源岩的热史以及成熟史提供基础理论支持,为研究走滑带地区地震的孕育过程提供相应的热动力学依据。
本研究下一步还需进行的工作有:①修改模型,调试参数,优化热模拟结果;②考虑走滑带受力形变对热模拟结果的影响;③模拟走滑带在海底热流和走滑摩擦2种热源机制影响下的热效应及产热对周围含油气盆地和断裂带地震孕育的影响。
高红芳, 2011, 南海西缘断裂带走滑特征及其形成机理初步研究, 中国地质, 38(3): 537-543. |
林长松、高金耀、赵俐红等, 2009, 南海西缘断裂带的地球物理特征及其构造地质意义, 海洋学报(中文版), (2): 97-103. |
刘海龄, 1999, 南沙西部海域伸缩型右旋走滑双重构造系统及其动力学过程, 海洋地质与第四纪地质, 19(3): 11-17. |
刘海龄、姚永坚、沈宝云等, 2015, 南海西缘结合带的贯通性, 地球科学, 40(4): 615-632. |
孟林、张健, 2014, 南海西南海盆残余洋脊岩浆活动机制的热模拟研究, 中国科学:地球科学, 44(2): 239-249. |
唐晓音、胡圣标、张功成等, 2014, 珠江口盆地大地热流特征及其与热岩石圈厚度的关系, 地球物理学报, 57(6): 1857-1867. |
王鹏程、李三忠、郭玲莉等, 2017, 南海打开模式:右行走滑拉分与古南海俯冲拖曳, 地学前缘, 24(4): 294-319. |
闫伟、武艳强、牛安福等, 2013, 基于择优的块体模型解算南北地震带中南段主要断层滑动速率, 中国地震, 29(1): 81-90. |
姚永坚、吕彩丽、王利杰等, 2018, 南沙海区万安盆地构造演化与成因机制, 海洋学报, 40(5): 62-74. |
尹凤玲、蒋长胜、韩立波等, 2018, 红河断裂带库仑应力演化及未来地震危险性估计, 地球物理学报, 61(1): 183-198. |
余尚江、成万里、陈波等, 2019, 南襄盆地及邻区地壳厚度与泊松比研究, 中国地震, 35(2): 286-294. |
张健、汪集旸, 2000, 南海北部陆缘带构造扩张的深部地球动力学特征, 中国科学D辑:地球科学, 30(6): 561-567. |
张健、宋海斌、李家彪, 2005, 南海西南海盆构造演化的热模拟研究, 地球物理学报, 58(6): 1357-1365. |
张健、董淼、吴时国等, 2017, 南沙海槽岩石圈热-流变结构与动力学演化分析, 地学前缘, 24(3): 27-40. |
周蒂、陈汉宗、吴世敏等, 2002, 南海的右行陆缘裂解成因, 地质学报, 76(2): 180-190. |
Gao X, Zhang J, Sun Y J, et al, 2012, A simulation study on the thermal structure of Manila trench subduction zone, Chin J Geophys, 55(1): 35-45. |
Gemmer L, Nielsen S B, Huuse M, et al, 2002, Post-mid-Cretaceous eastern North Sea evolution inferred from 3D thermo-mechanical modelling, Tectonophysics, 350(4): 315-342. |
Kato N, 2001, Effect of frictional heating on pre-seismic sliding:a numerical simulation using a rate-, state-and temperature-dependent friction law, Geophys J Int, 147(1): 183-188. |
Lü C L, Yao Y J, Gong Y H, et al, 2012, Deepwater canyons reworked by bottom currents:sedimentary evolution and genetic model, J Earth Sci, 23(5): 731-743. |
Morley C K, 2002, A tectonic model for the Tertiary evolution of strike-slip faults and rift basins in SE Asia, Tectonophysics, 347(4): 189-215. |
Zhang J, Xiong L P, Wang J Y, 2011, The characteristics and mechanism of geodynamic evolution of the South China Sea, Chin J Geophys, 44(5): 595-603. |