2. 涉县地震台, 河北涉县 056400;
3. 河北省地震局, 石家庄 050021
2. Shexian Seimic Station, Shexian 056400, Hebei, China;
3. Hebei Earthquake Agency, Shijiazhuang 050021, China
地形变作为地震前兆观测的基本手段,可以比较直接地显示震前近场与远场地壳垂向运动差异性的变化(牛安福等,2012)。地震学家将地面倾斜和升降作为重要地震前兆来论述(Housne,1995)。用地形变观测结果可以提取有效的地震前兆信息(徐东卓等,2017),也可检测球形自由振荡(孟方杰等,2018)。DSQ型水管仪是我国自行研制、用于测量地倾斜变化的仪器,河北涉县台水管仪安装于台站西侧约400m的山洞中,自安装以来运行稳定,但观测质量较易受到周边环境因素的影响。因地磁台建设需要,2013年3~5月对山洞附近地表土进行了大量外移,实施期间会对数据分析及应用造成一定影响(陈凯等,2018)。土体载荷的变化是否会对观测产生影响,是台站观测人员和地震预报专家密切关注的问题。在以往同类研究中,杜瑞林等(2004)采用Farrell(1972)的数值模拟方法计算了长江三峡水库蓄水引起的地形变变化量,毛伟建(1984)利用格林函数计算了地球对表面任何负载的响应,这2种载荷均属于面积大、体积大、质量大的情况。邱泽华(2004)分别用不同模型估计了观测点到干扰源的最小“安静”距离,而马栋等(2014)、张磊等(2016)根据其理论分析了载荷变化与蓟县台和永年台水管倾斜仪的异常关系,该模型将载荷变化视为作用在一个质点上。闫伟等(2015)基于不规则载荷模型计算了近地表的垂向位移理论值,但没有给出应用实例。
本文在前人工作基础上,研究了涉县台土体载荷变化与地倾斜的定量关系,即将载荷散点化处理,通过赋予散点不同的权重进行载荷重新分配,然后用矢量法获取水管仪各端点位移,根据倾斜量计算公式对土体载荷的影响进行计算并加以分析,以期为台站干扰因素分析和异常核实提供一定帮助。
1 台站及施工动土概述涉县地震台位于河北涉县河南店镇河二村西,为晋、冀、豫三省交界处,高程500m,属于涉县盆地南部边缘的低山丘陵地区,无较大断层通过台址(张丽晓等,2019)。形变山洞洞体进深约120m,引洞深约60m,岩石为下古生界中奥陶系石灰岩,洞体覆盖层为15m厚黄土。洞室内装有水管仪、垂直摆、伸缩仪,年温度变化小于0.1C°,资料质量较好。根据《地震台站观测环境技术要求》及《地震台站建设规范:地形变台站》(中国地震局,2004a、2004b)的要求,对周围环境进行了详细调查,距台站东南方向2km处为青红高速公路,东南方向1km处为县级公路,台站距11kV高压线0.5km、距矿山2.5km、距电气化铁路2.5km、距发电厂10km、距水位年涨落1~2m的清漳河1.5km,东北方向的饮用抽水井距台站0.4km,抽水量>100m3/d。从干扰的情况看,台站位置基本符合规范要求。
地磁场地建设主要集中在2013年3~5月。为满足地磁建设及环境要求,施工方对台站内大量土体进行了清理外运,其中树木及杂草暂不计重量,施工动土位置分为3个区域(图 1)。其中,A区域共计动土3015.5m3,形状近似于长50m、宽20m、高3m的长方体;B区域共计动土8220.5m3,可近似看作长55m、宽50m、高3m的长方体;C区域共计动土6171.8m3,也可近似看作长30m、宽20m、高10m的长方体;土方量总计约17408m3,B、C区域动土量最大,施工情况见表 1。
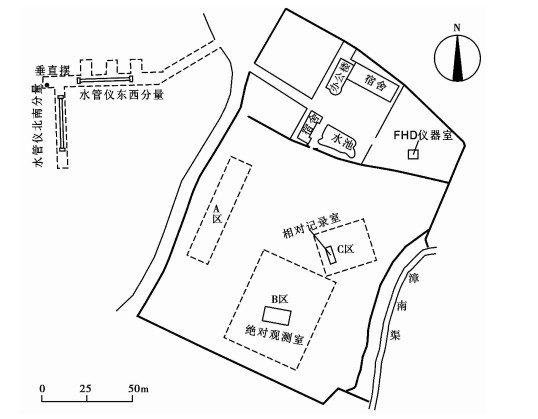
|
图 1 场地区域清理示意图 |
| 表 1 阶段性动土情况(单位:m3) |
将涉县台动土区域与山洞近似看为一个整体,并假定为密度均匀的半空间弹性体。动土区域变化设为集中载荷变化,以o为集中力F作用原点,x、y、z为直角坐标系三分量,M为受力点,r、R分别为M受力平面半径和三维空间受力半径,模型如图 2所示。

|
图 2 模型受力示意图 |
质点载荷模型这一问题最早由Boussinesq(1985)求得解答,所以通常称之为波西内斯克解
| $ {u_2} = \frac{{\left({1 + \mu } \right)F}}{{2\pi E}}\left[ {\frac{{{z^2}}}{{{R^3}}} + \left({1 - 2\mu } \right)\frac{1}{R}} \right] $ | (1) |
| $ R = \sqrt {{x^2} + {y^2} + {z^2}} $ | (2) |
其中,x、y、z为以集中力点为原点建立的空间直角坐标系的三分量,R为集中力点与作用点的距离,uz为产生的垂向位移,E为杨氏模量,μ为泊松比,F为载荷。仪器布设处的山洞岩体为完整灰岩,取E=3×1010Pa、μ=0.25,土体的比重为1.4t/m3,F=mg(m为运移土体的质量,g=9.8m/s2)。图 1中A区域的中心位置距台站水管仪E、W、S、N 4个端点的距离分别为155m、140m、145m、165m;B区域的中心位置距台站水管仪E、W、S、N 4个端点的距离分别为160m、185m、170m、190m;C区域的中心位置距台站水管仪E、W、S、N 4个端点的距离分别为220m、220m、215m、235m;三个区域与台站仪器布设位置的高差分别为0、-4m、-7m。
求出A区域4个端点产生的垂向位移,然后再对北南分量、东西分量分别做差值计算,可求出两分量的位移变化,分别为3.3375×10-7m和-3.8327 ×10-7m;B区域北南分量、东西分量的位移变化分别为6.952×10-7m、-9.4828×10-7m;C区域北南分量、东西分量的位移变化分别为3.3375×10-7m、-3.8372×10-7m。涉县台水管仪北南基线长度为30.2m,东西基线长度为28.23m。根据水管仪高差转换倾斜量公式(吴云,2009)有
| $ \Delta \varphi = 206265 \times \frac{{\Delta h}}{L} $ | (3) |
其中,Δφ为倾斜量,Δh为水管仪两端点的高差,L为水管仪基线长度,产生的单位为角秒。则A区域北南分量、东西分量的倾斜量变化分别为2.4ms、2.1ms;B区域北南分量、东西分量的倾斜量变化分别为4.7ms、-6.9ms;C区域北南分量、东西分量的倾斜量变化分别为2.3ms、-2.8ms;将3个区域的倾斜量相加则得到总的变化量,北南分量为9.4ms、东西分量为-7.6ms。由于涉县台水管仪每日变化量为2~5ms,可知动土对观测数据虽产生了一定影响,但按整月来计算,总体影响并不太明显。
2.2 二维载荷模型二维不规则载荷模型同样基于波西内斯克解的原理,将动土区域散点化处理,高度看作一个固定值。将动土的3个区域分别分割为n个网格,每个动土区域的长x平均分为n1份、宽y平均分为n2份,则n=n1×n2。F平均分布其上,则每个网格的载荷为Fi=F/n。
将载荷平均到每个网格内,计算出每个网格产生的位移,再对每个区域产生的位移进行叠加,最后将3个区域产生的总位移按照水管仪倾斜量公式(式(3))进行计算。增加网格数n,结果收敛于一个稳定值。经计算,A区域北南分量、东西分量产生的位移分别为1.4141×10-7m、-1.8172×10-7m;B区域北南分量、东西分量的位移变化分别为2.6047×10-7m、- 2.2376×10-7m;C区域北南分量、东西分量的位移变化分别为-3.7583×10-7m、- 1.62712×10-7m。A区域北南分量、东西分量的倾斜量变化分别为0.1ms、-1.3ms;B区域北南分量、东西分量的倾斜量变化分别为1.8ms、-1.6ms;C区域北南分量、东西分量的倾斜量变化分别为-2.6ms、-1.2ms;将3个区域的倾斜量相加则得到总的变化量,北南分量为2ms、东西分量为-4.2ms。与质点载荷模型相比,其收敛值小,结果的收敛特征也说明其结果的可行性和正确性,网格数n越大,越接近实际动土情况。
2.3 三维载荷模型三维载荷模型原理与二维载荷模型相同,根据动土范围把动土区域看作3个长方体,将x平均分为n1份、y平均分为n2份、z平均分为n3份,n=n1×n2×n3。将每个区域的总载荷平均分布到每个网格内,再对每个区域产生的位移进行叠加,最后将3个区域产生的总位移按照水管仪倾斜量公式(式(3))进行计算。增加网格数,结果收敛于稳定值。三维载荷模型建立后,经计算,A区域北南分量、东西分量产生的位移变化分别为1.4157×10-7m、-1.8202×10-7m;B区域北南分量、东西分量的位移变化分别为2.6111×10-7m、-2.2428×10-7m;C区域北南分量、东西分量的位移变化分别为-3.7648 ×10-7m、-1.6494×10-7m。A区域北南分量、东西分量的倾斜量变化分别为0.1ms、-1.3ms;B区域北南分量、东西分量的倾斜量变化分别为1.8ms、-1.6ms;C区域北南分量、东西分量的倾斜量变化分别为-2.6ms、-1.2ms;将3个区域的倾斜量相加则得到总的变化量,北南分量为2ms、东西分量为-4.2ms。同样,网格数越大,模型越接近直实情况,当网格数n大于3000时,与二维载荷模型相比,其结果趋于相同,三维载荷模型计算结果的收敛特征也说明了其结果的可行性和正确性。
2.4 观测曲线实际变化计算2012年1月~2014年12月涉县台水管仪每月的变化幅度,时间选取范围包括了动土开始前1年和动土完成后1年,每月变化量如图 3、图 4所示。
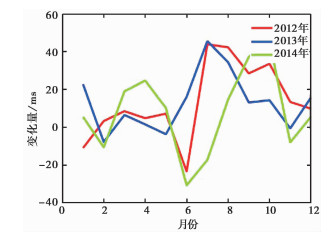
|
图 3 水管仪NS分量每月变化量 |
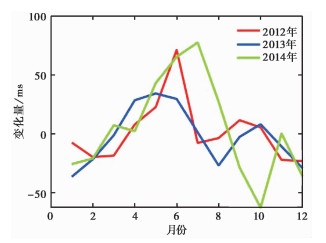
|
图 4 水管仪EW分量每月变化量 |
由图 3、图 4可以看出,水管仪每月的变化量呈不规则形态。北南分量的最大月变量为2012年7月的43.9ms、2013年7月的45.6ms和2014年10月的45.6ms;东西分量的最大月变量为2012年6月的71.1ms、2013年1月的-36.4ms和2014年7月的77.4ms。2012~2014年水管仪北南分量的平均月变化分别为13.4ms、13.2ms和8.0ms,东西分量的平均月变化分别为1.4ms、-2.3ms和4.0ms,可见在动土前后与动土期间并未出现明显的变化。
3种模型相比较,由质点载荷模型得出的位移量与倾斜量均较大,而理论上二维、三维载荷模型更接近实际动土情况,3种结果均表明土体载荷变化未对水管仪日常曲线的观测趋势造成影响。
2.5 内精度分析决定倾斜观测资料质量的内精度指标是调合分析得到的M2波潮汐因子和长周期拟合噪声水平(卢双苓等,2011),公式为
| $ \alpha = \frac{S}{R} $ | (4) |
式中,α为内精度,S为M2波的中误差,R为M2波的潮汐因子。通过内精度指标的计算和验证,能够客观公正地评价地形变观测资料的质量,以保证其在地震监测预报和科学研究等领域的可靠使用。计算2012年1月~2014年12月涉县台水管仪每月的内精度,时间选取范围包括动土开始前1年的每月精度值到动土完成后1年的每月精度值,结果如表 2、表 3所示。
| 表 2 水管仪NS分量内精度值 |
| 表 3 水管仪EW分量内精度值 |
2012~2014年水管仪北南分量的内精度年均值分别为0.0026、0.0030和0.0022,东西分量的内精度年均值分别为0.0019、0.0029和0.0018。可以看出动土前后的2012年、2014年与2013年动土期间有略微不同,2012年、2014年的内精度要比2013年高。将动土期间的3月、4月、5月与2012年和2014年的3月、4月、5月进行对比,2012年、2013年和2014年3个月的水管仪北南分量内精度平均值分别为0.34、0.43、0.20,东西分量内精度平均值分别为0.0020、0.0048、0.0022,可以看出动土时间段内水管仪两分量与2012、2014同时段相比,内精度明显较差。再将动土时间段的3个月与同年的前后月份进行对比,水管仪两分量3个月的均值分别为0.0043、0.0048,其余9个月的均值分别为0.0025、0.0022,可以看出动土时间段的内精度明显比同年度未动土时间段差。由上述数据可以得出,涉县台地磁场地施工动土对水管仪内精度产生了一定影响,导致观测资料质量变差。
2.6 观测数据的连续性或完整率对内精度的影响数据的连续性或完整率是保证观测质量的基本条件,也是衡量仪器是否正常工作的首要指标,只有达到一定规范标准才能对各种影响因素进行有效分析。统计涉县台水管仪2012~2014年的数据完整率,并查阅该期间的观测日志,发现影响因素有数据采集器、电源、人为干扰和气压变化等,其中人为调零、校准和电源故障是主要影响因素,按照要求,台站人员每年对仪器只做2次校准,以减少人为影响。统计结果表明,施工动土期间资料连续、未缺数,可以完好地进行理论计算及分析。2012年6月1~2日,因公用数据采集器遭雷击,造成缺测;2013年2月25~26日和8月29日,因电源故障又导致缺测,故相应月的内精度受影响变差,进一步说明施工动土期间载荷变化确实会造成观测资料内精度降低。
3 结论与讨论因地磁观测场地建设造成了涉县台土体载荷变化,本文分别用质点、二维、三维载荷模型解算理论值,发现施工对山洞水管仪的观测曲线没有明显影响,但会导致观测资料内精度有所降低。研究结果表明,二维、三维模型更接近真实情况,随着网格加密,2种模型的解渐趋一致。
然而,模型假设半空间弹性体密度均匀、各向同性,但实际施工动土区域与仪器布设位置并非如此理想,且地层结构又是分层的,故理论值可能存在一定误差。
致谢: 感谢闫伟副研究员、佘雅文博士在文章写作中给予的理论指导以及匿名审稿专家提出的修改意见。
陈凯、曹坤剑、易江, 2018, 重庆地震台BBVS-120与KS-2000型地震计系统性能对比分析, 高原地震, 30(1): 34-39. |
杜瑞林、乔学军、王琪等, 2004, 长江三峡水库蓄水荷载地壳形变-GPS观测研究, 自然科学进展, 14(9): 1006-1011. |
卢双苓、林秀娜、邢伟伟等, 2011, 泰安地震台伸缩仪运行分析, 地震地磁观测与研究, 32(4): 83-89. |
马栋、陈建国、张双凤等, 2014, 永年地震台水管加速N倾异常分析, 地震地磁观测与研究, 35(3-4): 192-197. |
毛伟建, 1984, 地球表面质量负荷的静态响应, 地球物理学报, 27(1): 74-83. |
孟方杰、张燕, 2018, 利用不同倾斜仪和应变仪检测地球自由振荡的对比与分析, 中国地震, 34(1): 133-140. |
牛安福、张凌空、闫伟等, 2012, 汶川地震近震源区地形变短期前兆现象的解析, 地震, 32(2): 52-63. |
邱泽华, 2004, 倾斜观测载荷干扰源最小"安静"距离理论分析, 地震, 24(4): 80-86. |
吴云, 2009, 地形变测量:试用本, 北京: 地震出版社.
|
徐东卓、尹海权、朱传宝等, 2017, 九寨沟7.0级地震前后地壳形变时空演化特征及相关问题的讨论, 中国地震, 33(4): 549-562. |
闫伟、牛安福、陈国琴, 2015, 不规则载荷影响地表近场垂向位移和倾斜观测的定量计算, 中国地震, 31(2): 297-307. |
张磊、邵永新、曹井泉等, 2016, 蓟县台水管倾斜仪NS向加速北倾异常分析, 大地测量与地球动力学, 36(4): 372-376. |
张丽晓、闫俊岗、谭青等, 2019, 河北南部及邻近地区中小地震震源机制特征分析, 地震地磁观测与研究, 40(3): 7-14. |
中国地震局, 2004a, GB/T 19531.3-2004地震台站观测环境技术要求第3部分:地壳形变观测, 北京: 地震出版社.
|
中国地震局, 2004b, DB/T T8.2-2003地震台站建设规范:地形变台站第2部分:钻孔地倾斜和地应变台站, 北京: 地震出版社.
|
Boussinesq J, 1885, Application des Potentiels à l'Etude de l'Equilibre et du Mouvement des Solides Elastiques, Paris:Gauthier-Villars. |
Farrell W E, 1972, Deformation of the earth by surface loads, Rev Geophys, 10(3): 761-797. |
Housner G W, 1995, Earthquakes and geological discovery, Earthquake Spectra, 11(1): 167-168. |
 2020, Vol. 36
2020, Vol. 36


