0 引言

据中国地震台网正式测定，2014年8月3日16时30分云南省昭通市鲁甸县(27.1° N，103.3°E)发生M_S6.5地震，震源深度12km。截至2014年8月11日08时00分，此次地震共记录到余震总数为1335个，其中5.0~5.9级地震0个，4.0~4.9级地震4个，3.0~3.9级地震8个^①。鲁甸地震是2000~2019年期间云南境内发生的最大地震，属于典型的浅源地震，地表震动强烈，加之震区人口稠密、建筑物抗震能力较弱、地质构造复杂，地震造成的次生灾害频发，震级不大却造成了重大人员伤亡和财产损失，因此引起了地震学界的广泛关注(房立华等，2014；刘成利等，2014；王未来等，2014；徐涛等，2014；徐锡伟等，2014；张广伟等，2014；张勇等，2014)。据云南省民政部门统计，截至2014年8月7日19时，此次地震共造成615人死亡、114人失踪、3143人受伤，22.97万人紧急转移安置，108.84万人受灾。

①https://www.cea.gov.cn/cea/xwzx/rdbd/5216253/index.html

徐锡伟等(2014)对鲁甸地震发震断层的判定研究认为，鲁甸M_S6.5地震是川滇菱形块体SSE向运动在青藏高原东缘与华南地块相互作用边界变形带上发生的一次中等强度地震，其发震断层为NW向的包谷垴-小河断裂，具有左旋走滑性质，属大凉山断裂南端部组成部分(徐锡伟等，2014；房立华等，2014；张勇等，2014)。刘成利等(2014)基于有限断层模型反演方法，采用区域宽频带数据反演得到了鲁甸M_S6.5地震的震源破裂过程，其结果显示此次地震的发震断层走向为NNW向，破裂主要以左旋走滑为主，起破点深度约为11km。张勇等(2015)进一步采用近震宽频带和强震资料以及远震体波资料进行反演，得到了鲁甸地震的破裂过程，认为鲁甸地震是在NW向主压应力与NE向主张应力的统一应力场下发生的2条共轭断层先后破裂的一次复杂地震事件。

王未来等(2014)采用双差定位方法对鲁甸M_S6.5地震序列进行重定位研究，其定位结果显示鲁甸地震主震位于27.11°N、103.35°E，震源深度约为15km；地震序列主要呈“L”形优势分布，呈现近垂直的震源分布特征，显示此次地震为走滑型，并存在2个不同方向的破裂面。张广伟等(2014)采用双差定位方法对鲁甸M_S6.5地震主震及余震序列进行了重新定位，其重定位结果显示鲁甸地震主震震源深度约为13.3km，与破裂过程显示的初始破裂深度较为接近，余震序列显示出近EW-NW向的不对称共轭状分布；小震分布展示出发震断层高倾角分布，且与包谷垴-小河断裂活动相关；其震源机制解结果显示主震质心深度约为5.0km，本次主震错断了互为共轭的2条断裂，认为这种共轭破裂模式与矩心深度较浅可能是本次地震致灾严重的重要原因。

王未来等(2014)的重定位结果沿纬度、经度和深度方向的定位误差分别为0.7km、0.8km、1.5km。房立华等(2014)的重定位结果给出的水平定位误差为0.4km，深度定位误差为1.8km。震源深度的定位误差明显大于水平位置的误差，因此对鲁甸地震主震震源深度进行精确测定具有研究意义。

地震射线追踪是地震定位、层析成像等应用领域的关键正演环节(李飞等，2013、2017a、2017b、2018；Li et al，2014)。传统的运动学射线追踪方法包括试射法(Langan et al，1985；Sun，1993；Sambridge et al，1995；徐涛等，2004)和弯曲法(Julian et al，1977；Thurber et al，1980；Um et al，1987)。试射法在全局搜索接收器方面效果较好，而弯曲法的计算效率较高。在前期的研究工作中，针对传统网格结构和层状结构在描述三维复杂地质模型时的困难，我们采用块状建模的介质描述方式，并发展了与之相适应的逐段迭代射线追踪方法(徐涛等，2004；Xu et al，2006、2010、2014；李飞等，2013)，可以快速获取地震射线路径和走时信息。基于前人对鲁甸地区速度结构的相关研究成果(熊绍柏等，1993；徐涛等，2014)，本文采用块状建模方法建立鲁甸地区地下三维速度结构模型，使用搜集到的主震震中距150km范围内的近震Pg波震相走时数据，通过逐段迭代射线追踪走时拟合，获得了鲁甸M_S6.5地震的震源深度。

1 三维地质模型中的快速射线追踪

在正演过程中，进行模型参数化时采用块状建模方法来描述三维复杂地质模型，并用三角形网格描述块体之间的间断面。在块状结构模型中，地质体被看作由大小不等、形状各异的地质块组成的集合体，每个地质块定义有各自的地质属性，如地震波速度、密度等，并与其他的地质块存在相邻的边界(李飞等，2013)。不同地质块之间的物性分界面由一系列的三角形面片拼接而成。三维地质体的描述采用“体-块-面-三角形-点”的层次结构(徐涛等，2004；Xu et al，2006、2010；李飞等，2013)。

在描述三维地质模型内部非均匀速度分布时，对地质体每个块体内部速度场进行单独定义，建立独自的三维速度网格，并在网格节点上定义速度值(李飞等，2013；Li et al，2014)。对于某块体内部任意点P(x，y，z)，首先找到该点落在网格中的位置，通过线性插值，由周围8个网格节点位置处的速度获得该点的速度v(x，y，z)，由此可以定义任意速度分布的三维地质模型。

对于非均匀速度分布的三维地质模型，李飞等(2013)、Xu等(2014)基于费马原理，发展了逐段迭代射线追踪方法。对于任意速度分布的非均匀介质，假设P_K-1、P_K+1为跨过界面的射线路径起始点和终止点，P_K为落在界面上的路径点，则满足界面方程

$ {x_k} = {x_k}\left({\xi, \eta } \right) $

(1)

其中，(ξ，η)为路径点P_K的坐标。

为了满足射线走时的费马原理，假设修正后的路径点位置为(ξ+Δξ，η+Δη)，射线轨迹走时T为路径点P_K坐标的函数，则有如下的偏导数方程成立

$ {\left. {\frac{{\partial T}}{{\partial \xi }}} \right|_{\left({\xi = \xi + \Delta \xi, \eta = \eta + \Delta \eta } \right)}} = 0, {\left. {\frac{{\partial T}}{{\partial \eta }}} \right|_{\left({\xi = \xi + \Delta \xi, \eta = \eta + \Delta \eta } \right)}} = 0 $

(2)

对公式(2)进行泰勒展开并保留一阶小量，可以得到射线路径中间点的一阶修正公式

$ \Delta \xi = \frac{{{U_{13}}{U_{22}} - {U_{23}}{U_{12}}}}{{{U_{11}}{U_{22}} - {U_{12}}{U_{21}}}}, \Delta \eta = \frac{{{U_{11}}{U_{23}} - {U_{21}}{U_{13}}}}{{{U_{11}}{U_{22}} - {U_{12}}{U_{21}}}} $

(3)

其中，(Δξ，Δη)为射线路径中间点坐标修正量，U_ij(i=1，2;j=1，2，3)为中间变量。

逐段迭代射线追踪方法属于弯曲法的范畴，通过对射线路径点采用一阶显式增量修正，射线追踪相对于传统的迭代法(Zhao et al，1992)更加高效省时。联合逐段迭代法与伪弯曲法(Um et al，1987)，提出了“连续三点”的射线追踪扰动修正方案，可以适应具有三维复杂非均匀介质且存在速度间断面的层状模型和块状模型，相对于传统的试射法和弯曲法具有更高的射线追踪效率，本文采用的射线追踪方法参考李飞等(2013)和Xu等(2014)给出的方法原理。

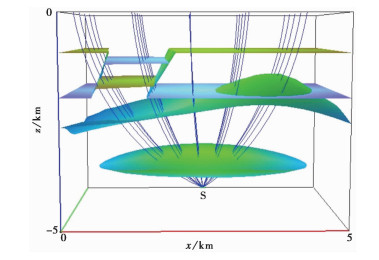
设计三维复杂块状模型中的射线追踪模型实验，如图 1所示，模型在x、y、z 3个方向的尺度均为5km，定义z轴向上为正，震源位于地下某一深度，台站均匀分布于地表，该组合模型包含断层、侵入体、透镜体等复杂地质构造。三维模型的尺度及震源、台站的空间位置可以在一定范围内任意设定。

2 数据及鲁甸地区三维速度模型构建 2.1 鲁甸M_S6.5地震近震Pg波震相走时数据

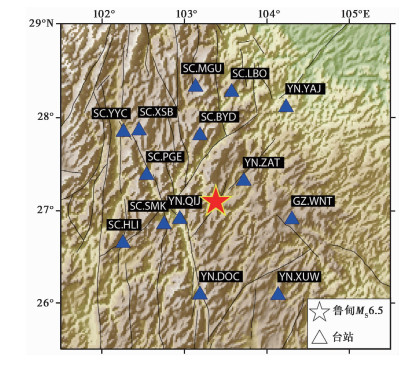
本文使用中国地震台网中心提供的鲁甸地震主震正式观测报告数据^②，搜集了鲁甸M_S6.5地震震中距150km范围内的近震Pg波震相数据，选取震中周边14个地震台站记录到的初至Pg波震相走时数据。鲁甸M_S6.5地震震中位置及本文使用的台站分布见图 2，由于鲁甸震区位于四川、云南交界位置，因此近震台站主要属于四川地震台网和云南地震台网，图中标注了各台网代码及台站代码，其中最近台为昭通台(YN.ZAT)，震中距约为41km。

② 中国地震台网中心，2014.地震编目系统正式观测报告.内部资料.

2.2 鲁甸地区三维速度模型构建

徐涛等(2014)利用宽角地震资料的初至波震相，通过有限差分反演揭示了丽江-清镇剖面的上地壳速度结构，由于该深地震测深剖面与鲁甸主震区的距离不超过50km，因此可以为鲁甸震区的地震定位、地震孕育机制等研究提供深部速度模型。其人工源速度剖面显示剖面结晶基底厚度平均约为2km，剖面结晶基底速度约为5.8km/s。

在进行鲁甸地震主震震源深度测定时，本文使用的鲁甸地区P波速度模型参考了熊绍柏等(1993)的壳内速度模型以及徐涛等(2014)的地壳浅部速度结构(表 1)。

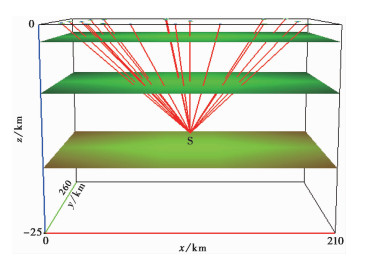
基于三维块状建模方法，并参照前人对该地区地壳浅部速度结构的相关研究成果(房立华等，2014；王未来等，2014)，建立鲁甸地区三维P波速度结构模型。在将经纬度坐标转换为直角坐标系后，建立了三维观测系统，震源近似位于三维模型中心位置，台站分布于地表，如图 3所示。该三维模型在水平方向的尺度分别为210km和260km，最大深度为25km，定义深度方向向上为正，模型在水平方向和垂直方向为非等比例表示。

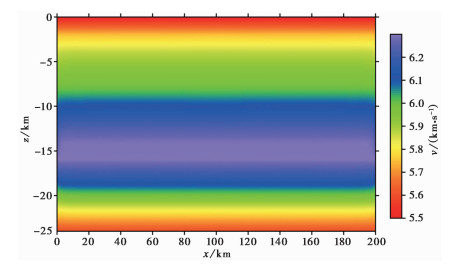
在三维模型中，水平方向速度均匀分布，纵向速度随深度增加线性递增，并在地下24km深度处存在1个低速层。各层介质内部速度由其层界面处的速度通过线性插值获得。鲁甸地区三维非均匀速度场在y=100km处的速度切片如图 4所示。

3 鲁甸M_S6.5地震震源深度测定

在前人对鲁甸M_S6.5地震重定位的研究结果中，震中位置的定位结果基本一致，而震源深度定位结果相差较大。因此，本文震中位置仍采用王未来等(2014)的双差定位结果(27.11°N、103.35°E)，在一定范围内对震源深度进行搜索，通过射线追踪走时拟合方法对鲁甸地震主震的震源深度进行测定。当震源位于地下某一深度(12km)时，采用逐段迭代射线追踪方法得到的鲁甸M_S6.5地震三维射线追踪结果见图 3。

不同震源深度的鲁甸M_S6.5地震三维射线追踪走时拟合曲线如图 5所示，当震源深度为12km时，通过三维模型中的射线追踪获得的鲁甸地震计算走时与台站记录到的观测走时之间的平均走时残差最小，约为0.75s。因此，认为鲁甸M_S6.5地震的最佳震源深度约为12km，该结果与国内外各相关研究机构的定位结果(刘成利等，2014；张广伟等，2014)基本一致。

4 结论与讨论

基于三维块状建模及逐段迭代快速射线追踪方法，本文建立了鲁甸地区地下三维速度结构模型，并进行了鲁甸M_S6.5地震的正演射线追踪模拟研究，将射线追踪获得的理论计算走时与震中周边150km范围内的地震台站记录到的近震初至Pg波震相数据进行拟合，获得鲁甸M_S6.5地震的最佳震源深度约为12km。该结果与前人相关研究成果基本一致，表明了本文采用的三维块状建模与逐段迭代射线追踪方法的有效性，为三维地质模型中的地震精定位方法研究奠定了基础。

本文建立的鲁甸地区三维速度结构模型相对较为简单，对于更复杂的三维模型中的地震精定位问题，地震定位与速度结构联合成像将是未来工作的重点。

致谢: 本文使用了中国地震台网中心提供的鲁甸M_S6.5地震的震相走时数据，部分图件使用GMT软件包绘制，匿名审稿专家提出了有益的修改建议，在此一并表示感谢。