0 引言

磁暴是空间天气扰动的主要形式之一，对卫星通讯、地面通讯、电网系统、油气管道运输系统等的正常运行均会产生严重影响(Albertson et al，1974；刘连光等，2014；张鹏飞等，2015)，因此，磁暴的快速自动识别至关重要。由于行星际激波通常和指向南的行星际磁场共同出现，因而急始(Sudden Commencement，简称SC)和磁暴往往同时出现(Curto et al，2007)。急始是识别磁暴发生的明显标志，可看作是磁暴的指示器。在急始后出现的磁暴称为急始型磁暴(Sudden Storm Commencement，简称SSC)，急始后未出现磁暴则将其称为急始脉冲(Sudden Impulse，简称SI)。

自格雷厄姆1722年第一次观测到磁暴变化至今，磁暴的观测工作者和建模工作者互相促进，尤其是随着地面以及卫星观测技术的不断提升，人们对磁暴的认识达到全新的高度(Loewe et al，1997；Curto et al，2007)。其中，较多学者从理论层面对磁暴及急始型磁暴机理进行了研究(Dessler et al，1960；Ondoh，1963；Burlaga et al，1969)，也有部分学者从地震预报的角度研究了磁暴与大震发震之间的规律(郭增建等，2018)，而更多的研究者是从磁场及实际生产生活(如电网、通信等)的角度研究如何快速、自动检测磁暴。Joselyn(1985)提出通过使用分钟值数据检测磁场快速变化的急始型磁暴检测方法；Shinohara等(2005)提出能够自动实时检测急始的太空天气监测系统，通过统计2000~2004年磁暴急始的振幅、上升时间、最大斜率，为急始检测系统制定了3条标准；Hafez等(2012、2013)将离散小波变换(DWT)以及最大交叠离散小波变换(MODWT)应用于1min、3s、1s尺度的地磁数据进行急始检测；Bailey等(2016)进一步对3种用于搜索以及定位急始型磁暴的方法(MODWT、一阶差分、AIC准则)进行对比研究，结果显示针对1s采样率的磁场数据，MODWT算法的效果最好，并且与Hafez等(2013)的算法得到的准确度大致相同。

上述研究均表明，磁暴急始检测拾取方法的精度提高，不仅得益于使用数据采样率的不断提高，即从最初的分钟值数据、3s采样数据逐渐发展为1s采样数据，更为重要的是取决于拾取技术的不断改进。而在1s尺度下对急始起跳时刻的拾取一直是磁暴领域的难点。为实现在秒采样率下的高精度磁暴自动拾取，本文基于Walsh变换与Akaike信息准则，针对性地设计出急始拾取算法，实现了基于1s采样率的磁场H分量数据的急始起跳点高精度定位拾取；并与多种传统方法如基于AIC的突跳拾取及最大交叠离散小波变换等进行比较。结果显示，根据本文提出的方法得到的拾取结果的平均偏差、标准差、误差区间均处于较低值，因此该方法是一种适合于秒数据尺度下急始定位的有效方法。

1 原理与方法 1.1 磁暴急始检测拾取方法

磁暴发生时，最典型的标志是其水平分量突然增加，呈现正脉冲变化，这种变化最接近于台阶函数，随着观测地区和时间的不同，形状也不尽相同(Araki，1977)，这种变化称为磁暴急始。詹贤鋆(1981)将磁暴的急始分为4种类型：立上急始型、负脉冲型、脉动型急始和阶梯状急始。值得注意的是，虽然在分钟尺度下磁暴急始的形态看起来非常尖锐，但在1s尺度下，地磁水平分量的上升十分缓慢，有些磁暴急始的水平分量一阶差分在0.2nT范围内，因此在1s尺度下对SC起跳时刻的拾取是一个难点。

参考Shinohara等(2005)的预警系统，采用磁暴急始的统计特征(包括持续时间、最大变化率、平均变化率、振幅等信息)，通过设定合适阈值来实现磁暴急始的粗检测，在此基础上，在秒数据尺度下利用Walsh-AIC算法实现磁暴急始的精确拾取。

1.2 Walsh变换

Walsh变换是以Walsh函数为基本函数的正交变换(Walsh，1923)，Walsh函数是取值只能为±1的完备正交函数系。由于只存在实数的运算，Walsh变换计算速度快、存储空间小。

Walsh函数系定义为

$ {w_k}\left( x \right) = \mathop \Pi \limits_{r = 0}^{P - 1} {\rm{sgn}}{\left( {\sin {2^{r + 1}}\pi x} \right)^{{k_r}}} $

(1)

其中，0≤x≤1；k=0，1，2，⋯；sgn为符号函数；k_r是序数k的P位二进制码中第r位的值，Walsh函数系的序共有4种，当k分别表示自然码、反自然码、Gray码、反Gray码时，Walsh函数序对应着Paley序、Hadamard序、Walsh序和反Walsh序(于洋，2016)。

假设序列长N=2ⁿ，则离散序列f(x)(x=0，1，2，⋯⋯，N-1)的Walsh变换为

$ W\left(u \right) = \frac{1}{N}{\sum\limits_{x = 0}^{N - 1} {f\left(x \right)\prod\limits_{i = 0}^{n - 1} {\left({ - 1} \right)} } ^{{b_i}\left(x \right){b_{n - 1 - i\left(u \right)}}}} $

(2)

其中，u=0，1，2，⋯，N-1；b_i(z)是z的二进制编码第i位的值。Walsh反变换的公式为

$ f\left(x \right) = {\sum\limits_{u = 0}^{n - 1} {W\left(u \right)\prod\limits_{i = 0}^{n - 1} {\left({ - 1} \right)} } ^{{b_i}\left(x \right){b_{n - 1 - i\left(u \right)}}}} $

(3)

对信号做Walsh变换得到变换系数，选择部分系数进行反变换，即可重构得到不同尺度的信号。

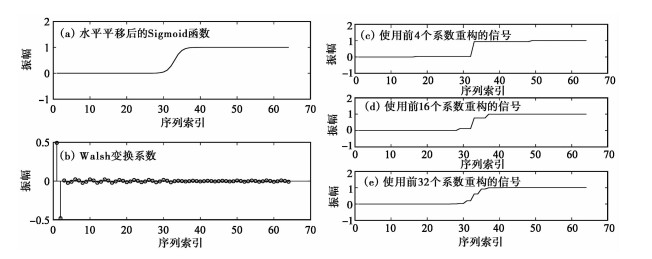
对64点水平平移后的Sigmoid函数做Walsh变换，并利用部分系数重构，如图 1所示。其中，图 1(a)为Sigmoid函数向右平移后的曲线；图 1(b)为图 1(a)对应的Walsh变换系数；采用Walsh序，图 1(c)、1(d)、1(e)分别为选择利用前4、16、32个系数对信号进行重构。信号的整体结构从不同尺度下重构出来，随着选择重构的系数增多，重构信号与原信号越来越接近，直至完全一致。

1.3 SC拾取方法

Akaike信息准则(Akaike Information Criteria，简称AIC)可用来确定2种统计特性不同的平稳序列的分界点，是用权衡统计法估计模型的复杂度和衡量此模型拟合优良度的标准(Akaike，1974)。目前，在地震学领域，Akaike信息准则主要应用于地震波初至信号的拾取(宋维琪等，2011；王洪超，2017；巩佳琦等，2018)。其主要原理如下：

将SC到来时刻前后拥有不同统计特征的有限长度序列利用自回归模型表示

$ x\left(t \right) = \sum\limits_{m = 1}^M {a\left(m \right)x\left({t - m} \right)} + \varepsilon \left(t \right) $

(4)

其中，M为自回归模型的阶数；a(m)为系数；ε(t)是具有零均值和方差为σ²的平稳白噪序列。

根据式(4)确定的自回归数学模型，在数据中k点的AIC值可定义为

$ {\rm{AIC}}\left(k \right) = \left({k - M} \right)\lg \left({\sigma _1^2} \right) + \left({N - k - M} \right)\lg \left({\sigma _2^2} \right) + C $

(5)

其中，σ₁²、σ₂²分别为分界点k两侧数据的方差；N为数据长度；C为常数。AIC函数在M过大的情况下需要对高阶矩阵求逆，导致运算量过大(巩佳琦等，2018)，Maeda(1985)提出改进算法，不需计算自回归系数，公式为

$ {\rm{AIC}}\left(k \right) = \left(k \right)\lg \left({\sigma _1^2} \right) + \left({N - k - M} \right)\lg \left({\sigma _2^2} \right) $

(6)

使得AIC(k)取得最小值的k为2个模型的最佳分界点。

然而，有研究结果显示通过AIC算法得到的SC时间可能会比实际时间晚数分钟(Bailey et al，2016)，即不能直接将AIC算法应用于地磁信号中SC起跳时刻的拾取，这主要是由于与地震信号相比，地磁信号并非围绕x轴上下波动，导致分界点两侧信号均值差异较为明显。假设SC实际起跳位置为k_n点，由于在1s尺度下信号上升非常缓慢，k_n点右侧若干点的值与左侧模型均值更加接近，拥有更相近的统计规律，因此用此算法直接作用于地磁信号所确定的起跳点会滞后于实际起跳位置。

为了解决上述问题，考虑采取增大起跳点两侧模型差异的方法。首先，对地磁水平分量H进行Walsh变换，变换采用Walsh序；然后，利用变换后得到的系数的主要成分重构地磁数据，对重构的地磁数据进行一阶差分处理，此时起跳点两侧数据拥有十分明显的统计规律差异，将缓慢渐变的2个模型转换为具有明显差异特征的2个差分模型；最后，利用公式(6)计算新模型的AIC曲线，使得曲线取得最小值点的k即为SC的起跳位置。

2 数据分析与算法测试 2.1 数据选择

本文的磁暴急始时刻采用国际地磁指数服务(ISGI)发布的SC目录^①，收集了2010~2015年的98个精确度为1s的SSC和SI事件进行起跳点拾取实验，地磁分数据及秒数据来自国家地磁台网中心^②。表 1列举了部分SC事件。

① http://isgi.unistra.fr/indices_dst.php

② www.geomag.org.cn

2.2 结果分析

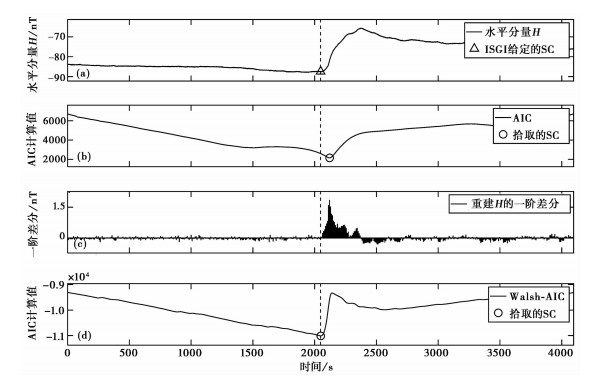
以拉萨台记录的2012年6月16日磁暴急始数据为例，对起跳点拾取过程作简要展示，如图 2所示。其中，图 2(a)为磁场水平分量曲线，数据起止时间为9︰21︰04~10︰29︰20，采样率为1s；图 2(b)为直接利用公式(6)对图 2(a)的数据计算得到的AIC曲线，最小值点对应的起跳点比实际起跳点明显滞后；图 2(c)为图 2(a)曲线经过Walsh变换重构后的差分曲线，起跳点两侧模型差异得到增强；图 2(d)为利用公式(6)对图 2(c)的数据计算得到的AIC曲线，曲线的最小值点即为Walsh-AIC算法确定的起跳点。由图 2可知，由传统AIC得到的起跳点位置明显晚于实际起跳点位置(ISGI给定)，而本文提出的Walsh-AIC算法拾取出的起跳点位置与实际起跳点位置非常接近，表明Walsh-AIC算法拾取精度相较于传统的AIC算法更高。

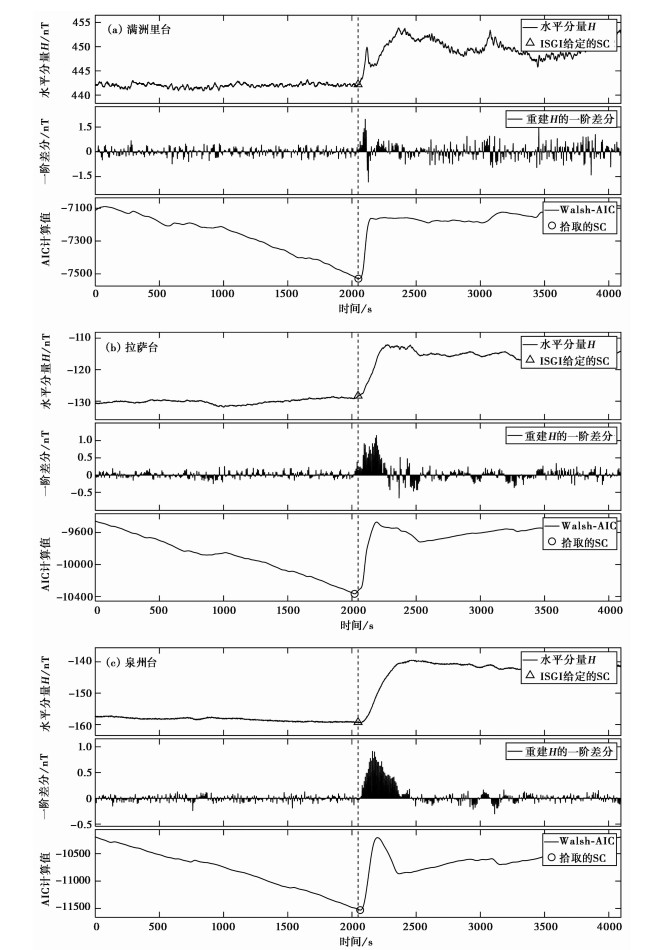
随机选出3组数据(采样率1s)，分别展示磁场H分量、Walsh重构后的一阶差分曲线以及AIC曲线，如图 3所示。其中，图 3(a)采用满洲里台2011年6月17日02︰04︰52~03︰13︰07的数据；图 3(b)采用拉萨台2013年6月23日03︰51︰28~04︰59︰43的数据；图 3(c)采用泉州台2013年12月13日12︰48︰40~13︰56︰55的数据。由于不同台站仪器情况、观测室湿度及周边环境的差异，曲线的质量也存在差异，在数据平滑及存在一定波动的情况下，利用本文算法得到的AIC曲线极小值点明显，与SC有较好的对应关系，表明该算法具有一定的抗噪能力。

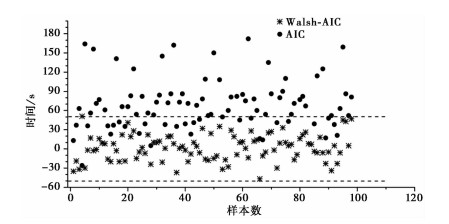
利用传统AIC算法以及Walsh-AIC算法对98组数据进行拾取，通过与标准起跳时刻做差，得到偏差分布情况，如图 4所示。由图 4可以看出，基于传统AIC算法的起跳点检测算法存在结果晚于实际起跳点的情况，Walsh-AIC有效避免了此问题，且结果均匀分布于起跳点两侧。

2.3 与其他方法的对比

目前，对磁暴急始起跳时刻进行拾取的方法主要有：使用db4小波，在3s采样间隔的数据上采用离散小波变换的多分辨率分析Ghamry方法(Ghamry et al，2013)；使用haar小波，在1s采样间隔数据上采用最大交叠离散小波变换的Hafez方法(Hafez et al，2013)；使用haar小波，在1s采样间隔数据上采用最大交叠离散小波变换的Bailey方法(Bailey et al，2016)；基于Akaike信息准则建立的起跳点检测方法(AIC方法)。将本文提出的算法与上述方法的磁暴急始拾取精度进行对比分析，结果如表 2所示，其中，ONW表示Onagawa台，KUJ表示Kuju台，KAG表示Kagoshima台，MSR表示Moshiri台，RIK表示Rikubetsu台。

经过对比分析可以看出，无论是定位结果的平均偏差还是标准差，Walsh-AIC算法均明显小于其他算法。同时，Walsh-AIC算法结果的误差关于0点的对称性极好。因此，采用Walsh-AIC算法拾取磁暴急始起跳时刻的精度较高。

3 结论

(1) 急始磁暴起跳点的自动拾取是地磁台网自动化建设中非常重要的一个环节，提高磁暴急始时刻拾取的准确性对磁暴报告自动产出至关重要。针对传统的起跳点拾取算法存在拾取出的时刻比实际时刻晚数分钟的问题，同时，为实现在1s采样率下的磁暴起跳点高精度拾取，本文基于地震学领域拾取地震波初至信号的AIC算法与Walsh变换，提出一种全新的算法——Walsh-AIC算法。

(2) 基于AIC准则的起跳点拾取算法是通过寻找2个统计规律不同的模型的最佳分界点来得到起跳时刻。然而，由于在1s尺度下地磁水平分量H变化过于缓慢，导致SC之后数分钟的数据与左右两侧模型均比较接近，从而降低了拾取精度。而Walsh-AIC算法通过Walsh变换重构后的差分处理，放大了SC两侧模型的统计特征差异，增大了起跳点数据的变化幅度，从而可以将SC的位置更明显地刻画出来。

(3) 为检验Walsh-AIC算法拾取磁暴急始时刻的效果，分别针对拉萨台、满洲里台、泉州台2010~2015年采样率1s的原始记录数据进行实际检验，对照的磁暴目录选取国际上权威的国际地磁指数服务(ISGI)发布的2010~2015年磁暴目录。结果显示，该算法不仅能够将急始磁暴起跳时刻的位置更加明显地刻画出来，而且能够有效避免传统起跳点识别算法中存在的识别出的起跳时刻结果晚于实际起跳点的情况。同时，由于算法试图寻找全局最小值点，结果受信号局部波动的影响较小。进一步选取不同SC自动拾取算法与Walsh-AIC算法进行拾取结果精度对比，结果显示，无论是定位结果的平均偏差还是标准差，Walsh-AIC算法均明显小于其他算法，同时Walsh-AIC算法结果的误差关于0点的对称性较好。

综上所述，本文提出的Walsh-AIC算法拾取磁暴急始起跳时刻的精度较高，适合于磁暴急始的拾取。

致谢: 国家地磁台网中心张素琴老师和中国地震局地球物理研究所李琪老师对论文进行了指导，国际地磁指数服务以及国家地磁台网中心为本文提供了相关数据，匿名审稿专家对论文的修改提出了建议，在此一并表示感谢。