0 引言

宽角反射(折射)资料重建地壳几何特征和速度结构对于理解地球内部物质组成有重要意义。地震波走时反演(Zelt，1999；徐涛等，2004；Bai et al，2007；王夫运等，2008；Nielsen et al，2009；Zhang et al，2009、2011；王晓等，2015；李飞等，2017、2018)是目前地壳介质重建的重要手段。

但是，地震波走时反演方法存在着一些固有的困难，例如走时震相识别困难、误差大，难以识别壳内二级间断面及精细结构的反射震相，主要利用反射震相而忽视了其他波场信息以及解的非唯一性等。因此，充分利用宽角反射(折射)资料中的动力学信息，并将地震勘探领域成熟的偏移成像技术运用其中，进而获取深部构造结构，是今后研究的重要途径和发展方向。本文利用四边形网格谱元法进行波场模拟，应用逆时偏移成像方法将合成地震记录偏移归位，以期验证逆时偏移成像方法在宽角地震资料处理解释中的适用性，为后续实际资料的处理应用提供科学的理论依据。

1 谱元法波场模拟

按照波动方程空间离散方式的不同，地震波波场数值模拟方法主要分为两大类：基于微分的方法(强形式)和基于积分的方法(弱形式)。前者主要包括有限差分法(Alford et al，1974；Lan et al，2011；兰海强等，2011；Zhang et al，2013a、2013b)、伪谱法(Fornberg，1988；Carcione et al，1993；Sidler et al，2013)；后者主要包括边界积分法(Schuster，1985；Bouchon et al，1989；徐世浙，1995)、有限元法(Lysmer et al，1972；徐世浙，1994；Kay et al，1999；Moser et al，1999)以及谱元法(Priolo et al，1991、1994；Patera，1984；王童奎等，2007a、2007b)等。

谱元法最早由Patera在1984年提出，后由Priolo等(1991)推广应用于地震波传播的数值模拟中。它兼顾了有限元法的灵活性和谱方法的指数收敛性，既具备有限元方法可以模拟任何复杂介质模型的韧性，又具备伪谱法的精度，具有高精度、高效率和弱频散等优点。该方法的基本思想是在每一个单元上采用伪谱法，以截断的正交多项式展开来表示基函数，在每个单元上，通过配置点进行插值(谱展开)，通过提高插值阶数增加解的精度(收敛性)。在单元上，根据不同的正交多项式展开方式皆可以得到不同的谱元法，主要包括切比雪夫(Chebyshev)谱元法和勒让德(Legendre)谱元法。由于Lagendre正交多项式展开时可以得到对角的质量矩阵和时间域的显式差分算法，因而在地震学中得到了较为广泛的应用。

本文采用四边形网格的谱元法(即经典的谱元法)，进行各向同性介质中的人工源宽角地震波传播的数值模拟。经典谱元法采用四边形或六面体网格，通过求解波形方程的弱形式，能够适应起伏的地表，保持物性的不连续性，并且能够精确地满足自由边界条件。在每个单元上采用非等间隔网格对地震波场进行谱展开，GLL(Gauss-Lobatto-Legendre)插值节点与积分节点重合，利用Legendre正交多项式在GLL点上构造Lagrange插值基函数，二维情形则是一维GLL积分的张量积(Komatitsch et al，1998)。由于Legendre正交多项式可以形成对角质量矩阵和时间域的显式差分算法，因而谱元法高效且高精度，在地震波模拟中得到广泛应用。二维弹性波波动方程可以表述如下

$ \rho \ddot u = div\left[ \sigma \right] + f $

(1)

其初始条件

$ u\left({x, 0} \right) = {u_0}\left(x \right) $

(2)

$ v\left({x, 0} \right) = {v_0}\left(x \right) $

(3)

式中，ρ=ρ(x)为介质的质量密度；σ为应力张量；f=f(x，t)为体力项；ü为质点的加速度向量；u(x，0)和v(x，0)分别表示质点在t=0时刻的位移场和速度向量，u₀(x)和v₀(x)分别表示初始位移和初始速度。应力由广义胡克定律定义

$ \sigma = c:\nabla u $

(4)

其中，c为弹性张量，“:”表示张量积，▽u为应变张量。

假定模拟区域为Ω，根据加权余量原理，在公式(1)两端同乘以一个任意测试函数ω，在物理域内进行积分，并利用分部积分得到波动方程的积分表示式，即弹性波方程的弱积分形式

$ \int\limits_\Omega {\rho \omega } \ddot u{\rm{d}}x + \int\limits_\Omega {\nabla \omega :} c:\nabla u{\rm{d}}x = \int\limits_\Omega {\omega f{\rm{d}}x} + \int\limits_{{\mathit{\Gamma }_{ext}}} {\omega T{\rm{d}}x} + \int\limits_{{\mathit{\Gamma }_{ext}}} {\omega t{\rm{d}}x} $

(5)

式中，T和t分别表示自由边界和人工边界上的外力，Г_int和Г_ext分别为自由边界条件和人工边界条件。在地震波数值模拟中，一般在某些方向上不可能无限延伸，所以需要引入人工边界。在自由边界条件上，弹性波动方程自动满足外力T=σ · n为0；在人工边界条件上需要特殊处理以压制虚假反射波。

相应地，有初始条件

$ \int\limits_\Omega {\rho \omega } u\left({x, 0} \right){\rm{d}}x = \int\limits_\Omega {\rho \omega } {u_0}\left(x \right){\rm{d}}x $

(6)

$ \int\limits_\Omega {\rho \omega } v\left({x, 0} \right){\rm{d}}x = \int\limits_\Omega {\rho \omega } {v_0}\left(x \right){\rm{d}}x $

(7)

基于积分法求解波动方程，通常将计算区域剖分成一系列不互相重叠的单元。如果模型是一维的，通常剖分成线段；如果模型是二维的，单元一般是规则四边形或曲线四边形，也可以是规则三角形或曲线三角形；如果模型是三维的，一般剖分成规则或曲面的四面体、六面体等，大小可以随空间位置而改变，因而具有较好的灵活性。

本文采用的四边形网格谱元法，通过将整个求解区域剖分成一系列单元后，在每个单元上进行数值积分来实现波动方程弱形式的离散化。

将式(5)离散化(不考虑人工边界条件)，可以得到如下常微分方程组

$ M\ddot u + Ku = F $

(8)

其中，M、K分别为质量矩阵和刚度矩阵；F为载荷向量。

2 模型实验

人工源宽角反射(折射)地震采用炸药震源，通常被当做一个爆炸点源。模拟中采用PML(Perfectly Matched Layer，完全匹配层)吸收边界(刘有山等，2012、2013、2014；Liu et al，2014、2017)，取得了较好的吸收效果，没有来自人工截断边界的明显的虚假反射波。

在模拟过程中，需要满足稳定性条件(式(9))和频散条件(式(10))(Liu et al，2017)

$ \Delta t \le \frac{{{h_{{\rm{min}}}} \times {\rm{CFL}}}}{{{v_{{\rm{P}}\max }}}} $

(9)

$ \Delta t \le \frac{{{v_{{\rm{S}}\min }}}}{{2.5{f_0} \times C}} $

(10)

式中，Δt为时间离散步长；h_min为谱元网格中的最小网格间距；v_Pmax为最大波速；CFL(Courant-Friedrichs-Lewy)为经验值，随着插值阶数的提高减小，对于四边形网格谱元法，CFL一般按照表 1取值；h为网格间距；f₀为主频；C同样为经验值，一般大于4；v_Smin为最小波速。只有同时满足稳定性和频散2个条件，才能得到较好的模拟效果。

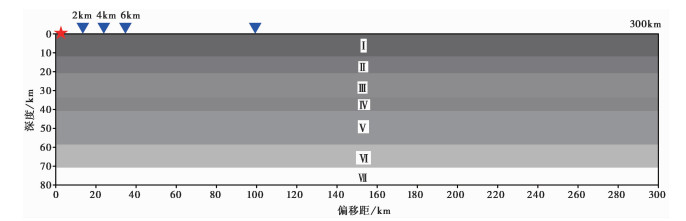
模型设计为X方向300km，Z方向80km，PML吸收边界厚度12km，均匀分层(图 1)，模型具体参数如表 2所示。设计的模型在尺度和主频上均尽量贴合实际情况。

采用规则四边形进行剖分，网格大小为420m×420m。离散时间步长Δt为0.0015s，时间总长度为110s，中心频率为5Hz，耗时约300000s。进行面波切除操作并将记录振幅单道归一化后，获得如图 2所示的模拟记录，图中可见震相明显，其中红色曲线为射线追踪得到的理论走时曲线。来自第Ⅲ层的反射震相能力较弱，原因是模型第Ⅳ层为低速层，且两层的速度差较小，致使第Ⅲ层反射能力不强。

3 逆时偏移成像研究

逆时偏移成像方法对于陡倾角构造的成像效果要优于其他偏移成像方法，可以适应任意的横向变速情况，具有准确的振幅和相位信息。实际地表情况往往十分复杂，断裂发育，壳内速度横向变化剧烈，其他的偏移方法很难得到较好的效果。

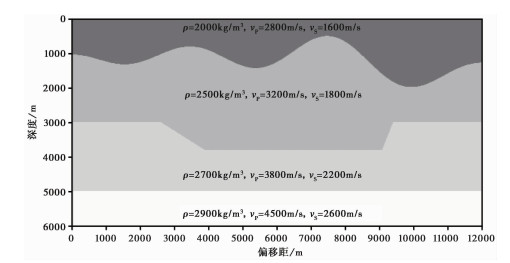
为验证逆时偏移成像方法的有效性，我们首先采取尺度相对较小的起伏地表及横向速度变化的模型(张智等，2013)进行实验，网格数1201×601，网格间距10m，检波器间距10m；震源位于地表，炮间距100m，共81炮，布置范围2000~10000m；震源为10Hz的雷克子波，采样间隔1ms，波场传播计算长度为6.0s，模型参数如图 3所示。

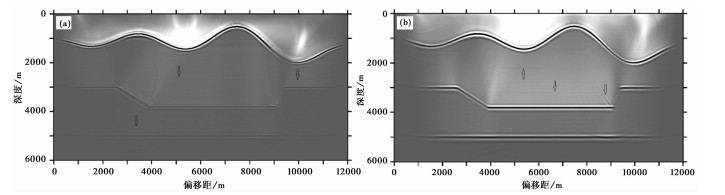
上述模型81炮叠加后的偏移结果(未滤波)如图 4所示，除个别区域存在较弱的串扰假象(图 4中箭头所指位置)，整体偏移效果较好。

将经典谱元法地震波数值模拟得到的人工源宽角地震记录(图 2)应用逆时偏移方法进行成像，测试炮数为4炮(SP1~SP4)，炮间距约为100km，单炮偏移平均耗时82h。单炮偏移归位并进行拉普拉斯滤波后的Z分量偏移图像如图 5所示。

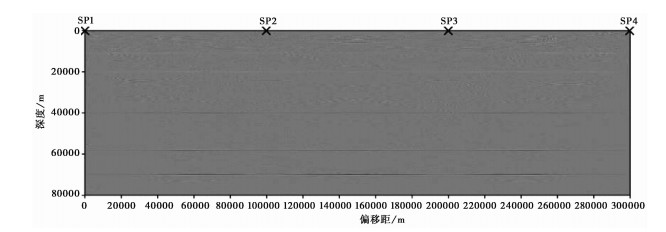
叠加单炮偏移结果获得最终偏移成像结果(图 6)，对比初始速度模型(图 1)可见，逆时偏移成像方法可以较好地将合成地震记录偏移归位，有效验证了该方法对于宽角地震资料的适用性。

4 结论

本文采用经典谱元法(四边形网格谱元法)正演模拟人工源宽角反射(折射)地震实验，实施了水平层状模型(大尺度)和起伏地表、横向速度变化剧烈的模型(相对小尺度)实验，并成功应用逆时偏移成像方法将合成地震记录偏移归位，与理论模型契合度较好。结果表明，逆时偏移成像方法可以应用于人工源反射(折射)地震资料的处理及结果解释中，为后续实际资料的处理解释提供了理论依据。逆时偏移成像方法在勘探领域已获得广泛应用，但在深地震测深领域的应用还有待进一步研究，本文利用模拟记录证实了逆时偏移成像方法可以应用于深地震测深资料，并提供了方法支持。

由于计算条件的制约，本文未能开展实际资料处理，在今后工作中拟将验证后的方法和参数应用于实际地震资料的处理解释中，以期获得地壳几何结构特征，并研究壳内变形方式和块体接触关系。